1. Of cats and cookies
Cookie Cats is a hugely popular mobile puzzle game developed by Tactile Entertainment. It's a classic "connect three"-style puzzle game where the player must connect tiles of the same color to clear the board and win the level. It also features singing cats. We're not kidding! Check out this short demo:
As players progress through the levels of the game, they will occasionally encounter gates that force them to wait a non-trivial amount of time or make an in-app purchase to progress. In addition to driving in-app purchases, these gates serve the important purpose of giving players an enforced break from playing the game, hopefully resulting in that the player's enjoyment of the game being increased and prolonged.
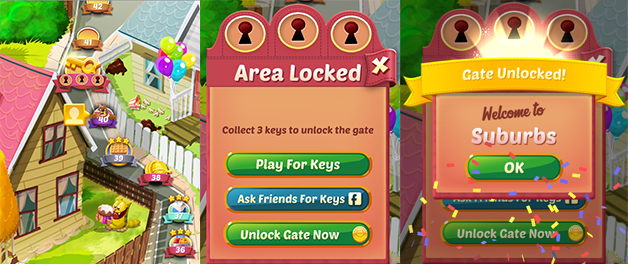
But where should the gates be placed? Initially the first gate was placed at level 30, but in this notebook we're going to analyze an AB-test where we moved the first gate in Cookie Cats from level 30 to level 40. In particular, we will look at the impact on player retention. But before we get to that, a key step before undertaking any analysis is understanding the data. So let's load it in and take a look!
# Importing pandas
import pandas as pd
# Reading in the data
df = pd.read_csv('cookie_cats.csv')
# Showing the first few rows
df2. The AB-test data
The data we have is from 90,189 players that installed the game while the AB-test was running. The variables are:
userid- a unique number that identifies each player.version- whether the player was put in the control group (gate_30- a gate at level 30) or the group with the moved gate (gate_40- a gate at level 40).sum_gamerounds- the number of game rounds played by the player during the first 14 days after install.retention_1- did the player come back and play 1 day after installing?retention_7- did the player come back and play 7 days after installing?
When a player installed the game, he or she was randomly assigned to either gate_30 or gate_40. As a sanity check, let's see if there are roughly the same number of players in each AB group.
# Counting the number of players in each AB group.
df['version'].value_counts()3. The distribution of game rounds

It looks like there is roughly the same number of players in each group, nice!
The focus of this analysis will be on how the gate placement affects player retention, but just for fun: Let's plot the distribution of the number of game rounds players played during their first week playing the game.
# This command makes plots appear in the notebook
%matplotlib inline
# Counting the number of players for each number of gamerounds
plot_df = df.groupby('sum_gamerounds')['userid'].count()
# Plotting the distribution of players that played 0 to 100 game rounds
ax = plot_df.head(n=100).plot(kind='hist')
ax.set_xlabel("Number of gamerounds")
ax.set_ylabel("Number of Player")4. Overall 1-day retention
In the plot above we can see that some players install the game but then never play it (0 game rounds), some players just play a couple of game rounds in their first week, and some get really hooked!
What we want is for players to like the game and to get hooked. A common metric in the video gaming industry for how fun and engaging a game is 1-day retention: The percentage of players that comes back and plays the game one day after they have installed it. The higher 1-day retention is, the easier it is to retain players and build a large player base.
As a first step, let's look at what 1-day retention is overall.
# The % of users that came back the day after they installed
df['retention_1'].mean()5. 1-day retention by AB-group

So, a little less than half of the players come back one day after installing the game. Now that we have a benchmark, let's look at how 1-day retention differs between the two AB-groups.
# Calculating 1-day retention for each AB-group
df.groupby('version')['retention_1'].mean()ret_1 = df.groupby('version')['retention_1'].mean()
import seaborn as sns
import matplotlib.pyplot as plt
sns.pointplot(data=ret_1)
plt.ylim(0.4, 0.5)6. Should we be confident in the difference?
It appears that there was a slight decrease in 1-day retention when the gate was moved to level 40 (44.2%) compared to the control when it was at level 30 (44.8%). It's a small change, but even small changes in retention can have a large impact. But while we are certain of the difference in the data, how certain should we be that a gate at level 40 will be worse in the future?
There are a couple of ways we can get at the certainty of these retention numbers. Here we will use bootstrapping: We will repeatedly re-sample our dataset (with replacement) and calculate 1-day retention for those samples. The variation in 1-day retention will give us an indication of how uncertain the retention numbers are.
# Creating an list with bootstrapped means for each AB-group
boot_1d = []
for i in range(500):
boot_mean = df.sample(frac=1,replace=True).groupby('version')['retention_1'].mean()
boot_1d.append(boot_mean)
# Transforming the list to a DataFrame
boot_1d = pd.DataFrame(boot_1d)
# A Kernel Density Estimate plot of the bootstrap distributions
boot_1d.plot(kind='kde')7. Zooming in on the difference
These two distributions above represent the bootstrap uncertainty over what the underlying 1-day retention could be for the two AB-groups. Just eyeballing this plot, we can see that there seems to be some evidence of a difference, albeit small. Let's zoom in on the difference in 1-day retention
(Note that in this notebook we have limited the number of bootstrap replication to 500 to keep the calculations quick. In "production" we would likely increase this to a much larger number, say, 10 000.)
# Adding a column with the % difference between the two AB-groups
boot_1d['diff'] = (boot_1d['gate_30'] - boot_1d['gate_40']) / boot_1d['gate_40'] * 100
# Ploting the bootstrap % difference
ax = boot_1d['diff'].plot(kind='kde')
ax.set_xlabel('Different betweeen two versions after 1 day')