Tutorial de pruebas T en R: Aprende a realizar pruebas T

Introducción

Supón que tienes dos grupos de equipos de ventas y quieres comprobar si el número medio de teléfonos móviles vendidos en una semana por ambos equipos es el mismo o no. ¿Cómo compararás el rendimiento? 

Tomarás el número medio de teléfonos móviles vendidos a 200 clientes aleatorios por los respectivos equipos y determinarás la diferencia. El primer equipo de marketing, de media, ha vendido 120 teléfonos, y el segundo equipo ha vendido 80. 

Por tanto, está claro que el primer equipo ha obtenido mejores resultados en ventas que el segundo. ¿Verdad? No podemos estar seguros: el conjunto de datos se recoge de clientes aleatorios y no representa a todas las personas que compraron el teléfono esa semana. 

Entonces, ¿cómo determinamos qué equipo tuvo mejores resultados? Utilizaremos una prueba t para saber si la diferencia entre las dos medias es real o solo suerte aleatoria.  

La prueba t es una hipótesis estadística que toma muestras de ambos grupos para determinar si existe una diferencia significativa entre las medias de los dos grupos. ¿Cómo funciona? Compara tanto la media muestral como las desviaciones típicas, teniendo en cuenta el tamaño de la muestra y el grado de variabilidad de los datos. 

En este tutorial, conoceremos la clasificación de las pruebas t (prueba t de una muestra, de dos muestras y de muestras pareadas) con ejemplos de código R y aprenderemos a interpretar los resultados. 

Nota: Si eres nuevo en R, haz el minicurso Introducción a la programación en R para comprender lo básico. 

Función t.test() en R

El lenguaje R nos proporciona una sencilla función integrada t.test para pruebas t de una muestra, dos muestras y pareadas. 

Hay dos formas de utilizar la función t.test: los métodos por defecto y de fórmula. 

Método por defecto 

Proporcionas muestras numéricas del grupo x y del grupo y, especificando la hipótesis alternativa, la media mu hipotética y el nivel de confianza del intervalo. Además, puedes realizar la prueba t pareada cambiando el argumento paired y la prueba t de dos muestras con varianza igual cambiando el argumento var.igual. 

t.test(x, y,
      alternative = c("two.sided", "less", "greater"),
      mu = 0, paired = FALSE, var.equal = FALSE,
      conf.level = 0.95, ...)

Método de fórmula

En este método, proporcionas la fórmula x~y, donde x es un vector numérico o una columna de los datos, e y es una columna binaria que contiene los tipos de grupos.     

t.test(formula, data, subset, na.action, ...)

Cómo realizar la prueba t de una muestra en R

La prueba t de una muestra es la hipótesis estadística para comprobar si existe una diferencia significativa entre la media muestral y la hipótesis o media poblacional supuesta. La prueba compara la media muestral con la media hipotética, teniendo en cuenta la variabilidad de los datos. 

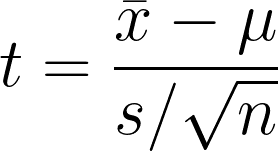
• x̄₁ = Media muestral
• μ = Media hipotética poblacional
• s = Desviación típica de la muestra
• n = Tamaño de la muestra

En este tutorial, utilizaremos el conjunto de datos de R Carbon Dioxide Uptake in Grass Plants para ejemplos de código de pruebas t. El conjunto de datos tiene 84 filas y 5 columnas, y se recopiló a partir de un experimento para probar la tolerancia al frío de la especie de pasto Echinochloa crus-galli. Tendremos en cuenta sobre todo las columnas Uptake, Treatment y Type para nuestras pruebas. 

head(CO2)

En el ejemplo, utilizaremos la columna conc (concentraciones de dióxido de carbono) del conjunto de datos. 

Podemos observar la media, la distribución y los valores atípicos mediante un diagrama de caja. 

boxplot(CO2$conc)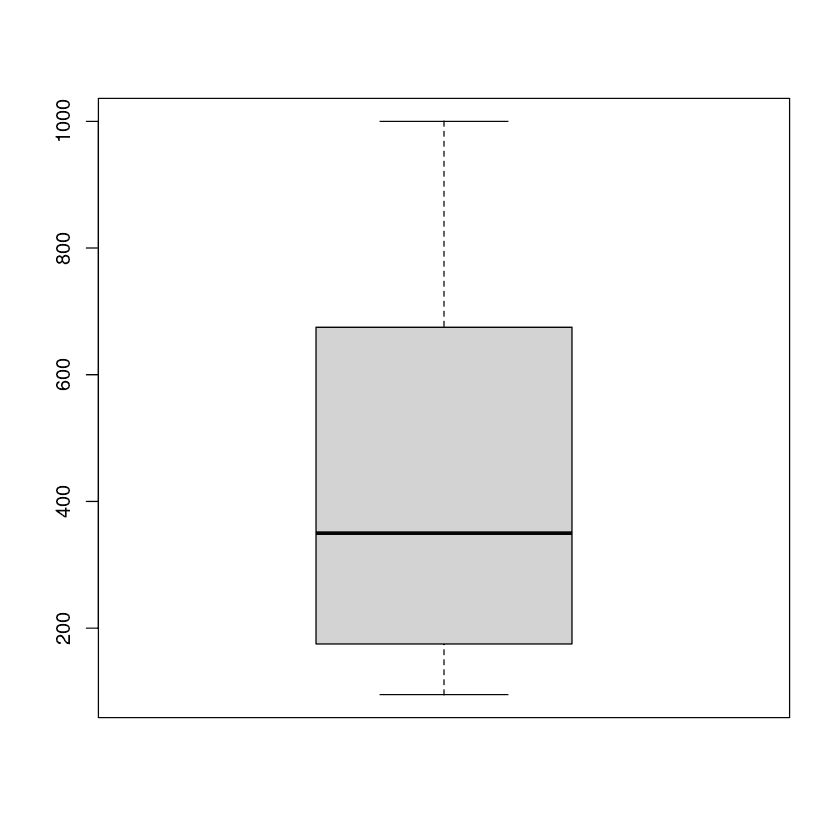

Para una prueba t de una muestra, utilizaremos `t.test(x,mu=0)`. x es la variable y mu está establecida por la hipótesis nula. En nuestro caso, es 550. 

t.test(CO2$conc, mu = 550)

Resultado:

La concentración de dióxido de carbono no es igual a 550 y es significativamente inferior a la media hipotética poblacional. 

One Sample t-test

data:  CO2$conc
t = -3.5617, df = 83, p-value = 0.0006134
alternative hypothesis: true mean is not equal to 550
95 percent confidence interval:
370.7805 499.2195
sample estimates:
mean of x
      435 

Cómo realizar la prueba t de dos muestras en R

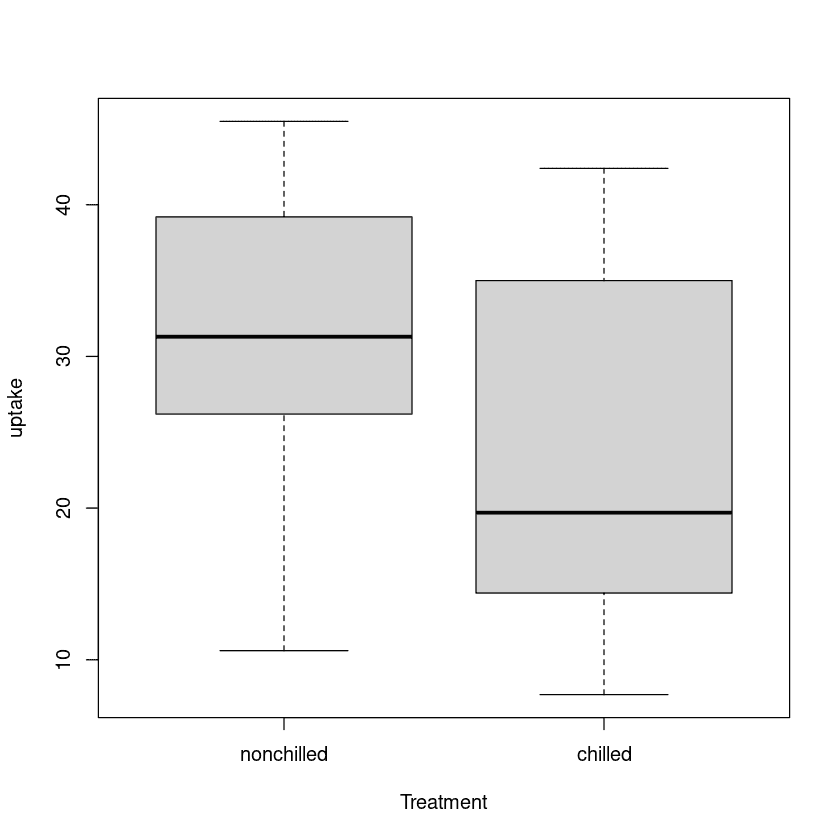
En las pruebas t de dos muestras, compararemos las tasas de absorción de dióxido de carbono de dos tipos de tratamiento: sin frío y con frío. 

Podemos visualizar la distribución de dos grupos mediante un diagrama de caja.  

plot(uptake ~ Treatment, data=CO2)

Prueba t de dos muestras de Welch

Es una hipótesis estadística que investiga si existe una diferencia significativa entre la media de dos grupos independientes que pueden tener varianza desigual. La prueba compara las medias de dos grupos teniendo en cuenta la variabilidad dentro de cada grupo.  

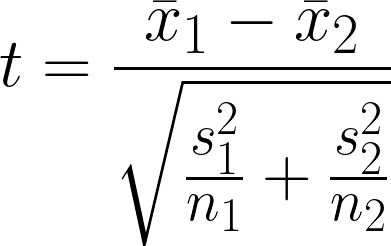
• x̄₁ = Media muestral del primer grupo
• x̄₂ = Media muestral del segundo grupo
• n₁ = Tamaño de la muestra del primer grupo
• n₂ = Tamaño de la muestra del segundo grupo
• s₁² = Varianza muestral del primer grupo
• s₂² = Varianza muestral del segundo grupo

Por defecto, la función t.test() supone que la varianza de dos grupos es desigual (var.equal=FALSE). Por tanto, no tenemos que hacer ningún cambio. 

Utilizamos el método de fórmula para obtener los resultados de la prueba t, donde Uptake es un vector numérico y Treatment es una columna de categoría binaria del conjunto de datos CO2. 

t.test(uptake ~ Treatment, data = CO2)

Resultado:

Hay una diferencia significativa en las medias de los dos grupos, y el grupo sin frío tiene una absorción mayor que el grupo con frío. 

 Welch Two Sample t-test

data:  uptake by Treatment
t = 3.0485, df = 80.945, p-value = 0.003107
alternative hypothesis: true difference in means between group nonchilled and group chilled is not equal to 0
95 percent confidence interval:
  2.382366 11.336682
sample estimates:
mean in group nonchilled    mean in group chilled
                30.64286                 23.78333  

Prueba t de dos muestras con varianza igual

La prueba t de dos muestras es un contraste de hipótesis para determinar si existe una diferencia significativa entre la media de dos grupos independientes, suponiendo que la varianza de los dos grupos sea igual. La prueba compara las medias de dos grupos teniendo en cuenta la variabilidad dentro de cada grupo. 

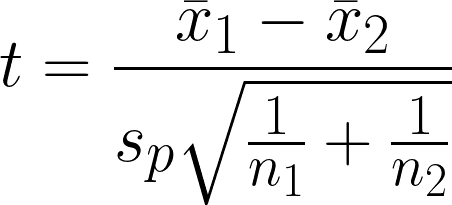
• x̄₁ = Media muestral del primer grupo
• x̄₂ = Media muestral del segundo grupo
• n₁ = Tamaño de la muestra del primer grupo
• n₂ = Tamaño de la muestra del segundo grupo
• s_p = Desviación típica agrupada

Para realizar pruebas t de dos muestras con varianza igual, tenemos que establecer var.equal TRUE y volver a ejecutar la prueba con la misma fórmula y el mismo conjunto de datos.

t.test(uptake ~ Treatment, data = CO2, var.equal = TRUE)

Resultado:

Como podemos ver, obtuvimos resultados similares en cuanto a que existe una diferencia de media significativa entre los dos grupos.

Two Sample t-test

data:  uptake by Treatment
t = 3.0485, df = 82, p-value = 0.003096
alternative hypothesis: true difference in means between group nonchilled and group chilled is not equal to 0
95 percent confidence interval:
  2.38324 11.33581
sample estimates:
mean in group nonchilled    mean in group chilled
                30.64286                 23.78333

Cómo realizar la prueba t pareada en R

La prueba t pareada es una hipótesis estadística que se utiliza para determinar si existe una diferencia significativa entre las medias de dos muestras relacionadas o pareadas. Calcula el valor de la prueba t comparando las diferencias entre las observaciones pareadas teniendo en cuenta la variabilidad dentro de la diferencia. 

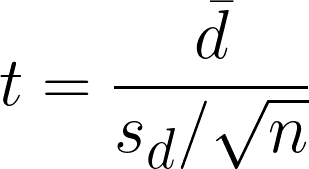
• dࠡ = Diferencias de media en observaciones pareadas
• s_d = Diferencias de la desviación típica de la muestra
• n = Número de pares

Para realizar la prueba t pareada en R, tenemos que establecer paired argument TRUE y volver a ejecutar la prueba con la misma fórmula y el mismo conjunto de datos.

t.test(uptake ~ Treatment, paired = TRUE, data = CO2)

Resultado:

Existe una diferencia estadísticamente significativa entre las medias de los dos grupos teniendo en cuenta el valor p y t. 

Paired t-test

data:  uptake by Treatment
t = 7.939, df = 41, p-value = 8.051e-10
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
5.114589 8.604458
sample estimates:
mean difference
      6.859524 

En el segundo ejemplo, factorizaremos la tasa de absorción de dos tipos de la misma planta. Uno es originario de Quebec y otro de Misisipi.

plot(uptake ~ Type, data=CO2)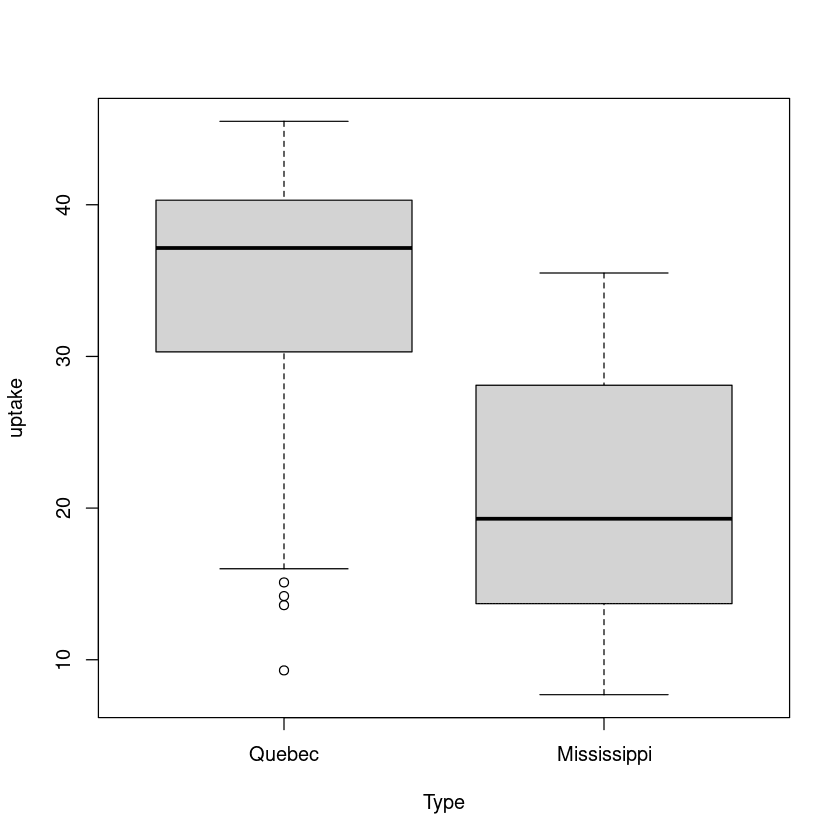

Comprobemos los resultados de la prueba t pareada sustituyendo Treatment por tipo en la fórmula. 

t.test(uptake ~ Type, paired = TRUE, data = CO2)

Resultado:

De nuevo, hay una diferencia significativa entre la media del grupo de Quebec y la del grupo de Misisipi. 

 Paired t-test

data:  uptake by Type
t = 11.374, df = 41, p-value = 2.937e-14
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
10.41177 14.90727
sample estimates:
mean difference
      12.65952  

Experimenta el DataCamp Workspace Prueba t en R. Incluye fuentes de código y resultados. También puedes duplicar Workspace y empezar a practicar con ejemplos diferentes. 

Nota: Una sólida base estadística te será útil, independientemente del sector al que pertenezcas. La estadística es la columna vertebral de la IA moderna, y deberías comenzar tu viaje con el programa de habilidades Fundamentos de estadística con R.

Cómo interpretar los resultados de la prueba t en R

Estamos generando los resultados, pero ¿qué significan df, valor p, hipótesis alternativa o estimaciones muestrales? En esta sección, aprenderemos a interpretar los resultados de la prueba t en R. 

Empecemos creando dos grupos mediante la función rnorm y ejecutemos las pruebas t de dos muestras. 

set.seed(125)

group1 <- c(rnorm(100, mean = 24, sd = 3))
group2 <- c(rnorm(100, mean = 43, sd = 2.4))

t.test(group1, group2)

Salida:

 Welch Two Sample t-test

data:  group1 and group2
t = -47.765, df = 179.99, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-19.51569 -17.96722
sample estimates:
mean of x mean of y
24.30063  43.04208 

• datos: los datos utilizados en la prueba t de dos muestras (group1 y group2) 
• t: estadística de prueba t. El valor t negativo de -47,765 indica que la media muestral de group1 es significativamente menor que la de group2.
• df: es el grado de libertad asociado al valor de la prueba t.
• valor p: indica la significación estadística del resultado. El valor p es 2.2e-16, que es inferior a alfa (0,005), lo que indica que la probabilidad de obtener por azar una diferencia tan grande entre los dos grupos es muy pequeña.
• hipótesis alternativa: podemos establecer la hipótesis alternativa. En nuestro caso, se estableció para comprobar si la verdadera diferencia de medias no es igual a cero.
• intervalo de confianza del 95 %: existe una confianza del 95 % en que en las medias poblaciones reales la diferencia entre los dos grupos esté dentro del intervalo de -19,51569, -17,96722.
• estimaciones muestrales: nos indican las medias muestrales de cada grupo, donde group1 y group2 son 24,30063 y 43,04208, respectivamente. Significa que, de media, group2 tiene un valor más alto que group1. 

Hay dos hipótesis para la prueba t:

1. H₀: µ₁ = µ₂: las dos medias poblacionales son iguales.
2. H_A: µ₁ ≠µ₂: las dos medias poblacionales no son iguales.

En conclusión, los resultados de la prueba t de dos muestras de Welch sugieren que hay pruebas sólidas de que existe una diferencia estadísticamente significativa entre group1 y group2. 

Conclusión 

En este tutorial, hemos aprendido sobre las pruebas t de una muestra, dos muestras y pareadas con ejemplos de programación en R y sobre cómo interpretar el resultado. 

La prueba t es una de las muchas herramientas estadísticas utilizadas en el contraste de hipótesis, y si quieres aprenderlo todo sobre el contraste de hipótesis, haz el curso interactivo Contraste de hipótesis en R. El curso abarca pruebas t, ANOVA, pruebas de proporciones y pruebas de ji cuadrado.

También puedes ir más allá e inscribirte en nuestro programa de carrera Estadístico con R para dominar las habilidades esenciales y conseguir un trabajo como estadístico.