Lógica difusa en IA: Principios, Aplicaciones y Guía de Implementación en Python

En los problemas del mundo real, las decisiones no pueden clasificarse como estrictamente verdaderas o falsas, sino que se sitúan entre parcialmente verdaderas y parcialmente falsas. Aquí es exactamente donde entra en juego la lógica difusa. Maneja conceptos que no están definidos con precisión, sino que aparecen en un espectro de posibilidades. 

Al introducir la flexibilidad para trabajar con incertidumbres y datos imprecisos, la lógica difusa refleja los procesos humanos de toma de decisiones, subsanando las deficiencias de los sistemas lógicos binarios tradicionales.

Aquí quiero explorar los principios, la arquitectura y las aplicaciones de la lógica difusa en la IA, destacando cómo permite un razonamiento mejorado y una toma de decisiones eficaz en entornos complejos. Si acabas de iniciar tu andadura en la IA, te recomiendo que consultes el itinerario de habilidades Fundamentos de la IA para ayudarte en el camino.

¿Qué es la lógica difusa?

La lógica difusa (FL) es un método de razonamiento que imita la toma de decisiones humana al considerar grados de verdad entre SÍ y NO, a diferencia de la lógica binaria, que da estrictamente VERDADERO o FALSO. Desarrollada por Lotfi Zadeh, la lógica difusa asigna posibilidades a las entradas, lo que permite un razonamiento matizado y flexible.

Lógica difusa frente a lógica binaria

Veamos con más detalle las diferencias entre la lógica difusa y la lógica binaria o booleana:

• Lógica binaria: Funciona con entradas exactas, produciendo salidas VERDADERO o FALSO.
• Lógica difusa: Permite estados intermedios, como mucho o poco, para una toma de decisiones más realista.

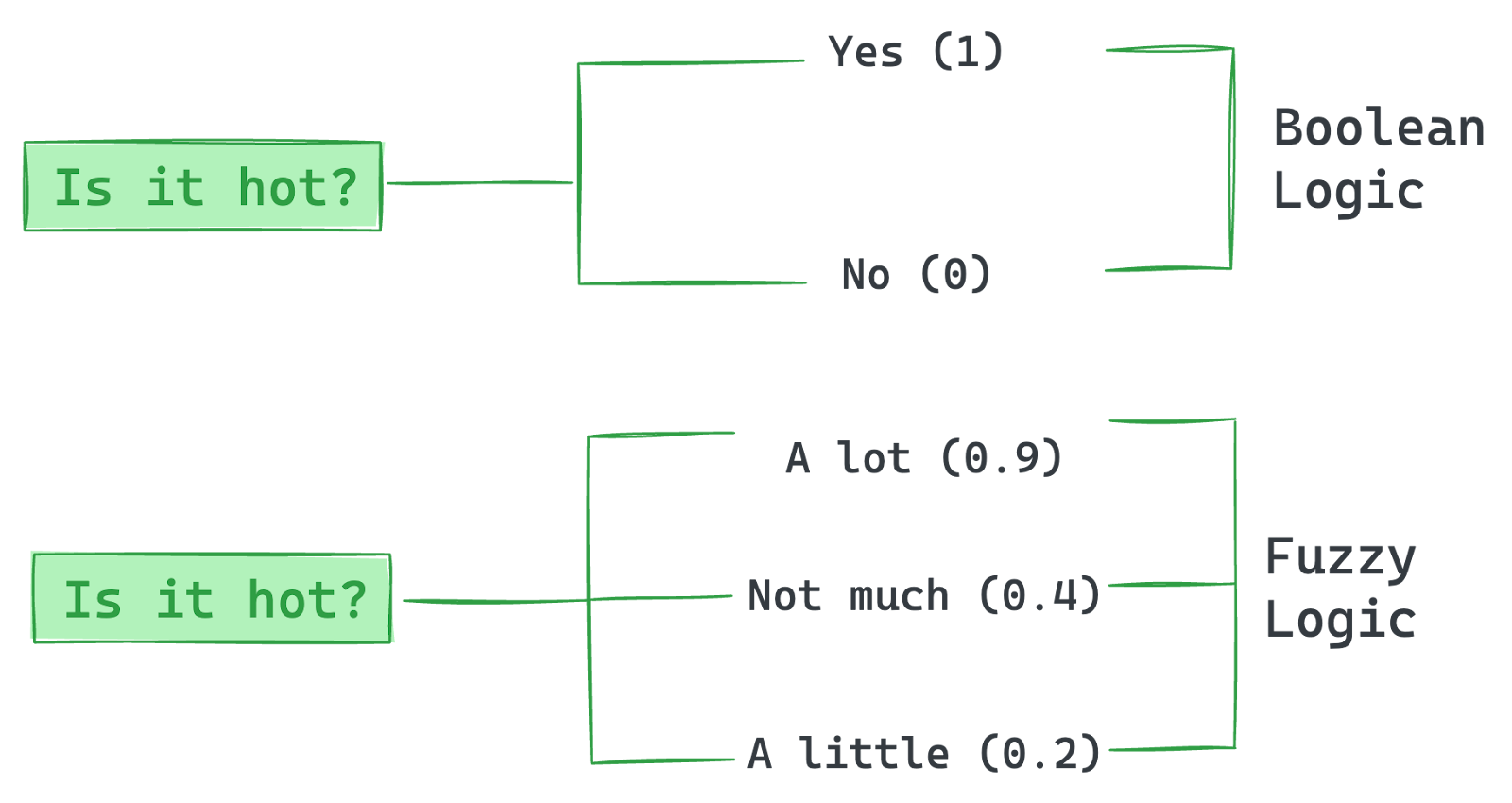
Imagen del autor

Importancia de la lógica difusa en la IA

La lógica difusa es crucial en la IA para manejar la incertidumbre, la ambigüedad y los datos imprecisos, permitiendo a los sistemas tomar decisiones de forma más parecida a los humanos, con varias características que imitan nuestro comportamiento a la hora de tomar decisiones: 

• Funciona con entradas imprecisas
• Proporciona transiciones más suaves entre estados
• Permite razonar con matices en entornos complejos

Para explorar los conceptos más amplios de la IA y sus aplicaciones, considera este curso DataCamp sobre Inteligencia Artificial.

Aplicaciones de la lógica difusa en el mundo real

La lógica difusa está detrás de muchas de nuestras tecnologías cotidianas: 

• Electrodomésticos: Optimizar el rendimiento de lavadoras y aparatos de aire acondicionado
• Sistemas de automoción: Mejorar el control de crucero y el cambio de marchas
• Diagnóstico médico: Evaluar síntomas de gravedad variable
• Sistemas de control: Gestionar la automatización industrial y las centrales eléctricas

El razonamiento similar al humano de la lógica difusa la convierte en una poderosa herramienta de la IA para gestionar la incertidumbre y la complejidad.

Comprender los fundamentos de la lógica difusa

Ahora que ya conocemos la definición clave de la lógica difusa y su uso en la IA, veamos algunos de los conceptos clave con más detalle.

Conjuntos difusos y funciones de pertenencia

La Lógica Difusa introduce el concepto de conjuntos difusosque se diferencian de los conjuntos clásicos en que permiten la pertenencia parcial en lugar de la inclusión o exclusión estricta.

En los conjuntos clásicos, un elemento

• Pertenece a un conjunto (valor de pertenencia = 1) 
• No pertenece (valor de pertenencia = 0)

Los conjuntos difusos, sin embargo, admiten grados de pertenencia, representados por valores entre 0 y 1.

La función de pertenencia es un concepto básico de la lógica difusa, que asigna los valores de entrada a su grado de pertenencia a un conjunto.

Por ejemplo, para determinar si una temperatura es "caliente", la función de pertenencia asigna un grado de verdad que va de 0 (nada caliente) a 1 (totalmente caliente), con valores intermedios que representan una verdad parcial.

Esta flexibilidad permite a la lógica difusa manejar eficazmente la incertidumbre y la imprecisión.

Reglas difusas y sistemas de inferencia

La lógica difusa funciona mediante reglas IF-THEN, que expresan relaciones entre entradas y salidas de forma difusa. Por ejemplo:

• SI la temperatura es "moderadamente caliente" ENTONCES la velocidad del ventilador es "media".

Estas reglas son procesadas por los sistemas de inferencia difusa, que combinan múltiples reglas difusas para tomar decisiones. El proceso implica:

1. Evaluar el grado de verdad de cada regla en función de los valores de entrada.
2. Combinando los resultados de todas las reglas aplicables mediante operaciones lógicas.
3. Generar una salida difusa, que luego se convierte en un valor preciso mediante métodos de defuzzificación.

Esta estructura permite a los sistemas de lógica difusa emular el razonamiento humano, lo que los hace valiosos en aplicaciones como los sistemas de control, el diagnóstico médico y la inteligencia artificial.

Al aprovechar los conjuntos difusos, las funciones de pertenencia y los sistemas de inferencia, la lógica difusa proporciona un marco sólido para manejar la imprecisión y ofrecer una toma de decisiones matizada.

Arquitectura de un sistema de lógica difusa

Un sistema de lógica difusa consta de cuatro componentes clave que trabajan juntos para procesar las entradas, aplicar un razonamiento similar al humano y producir salidas procesables.

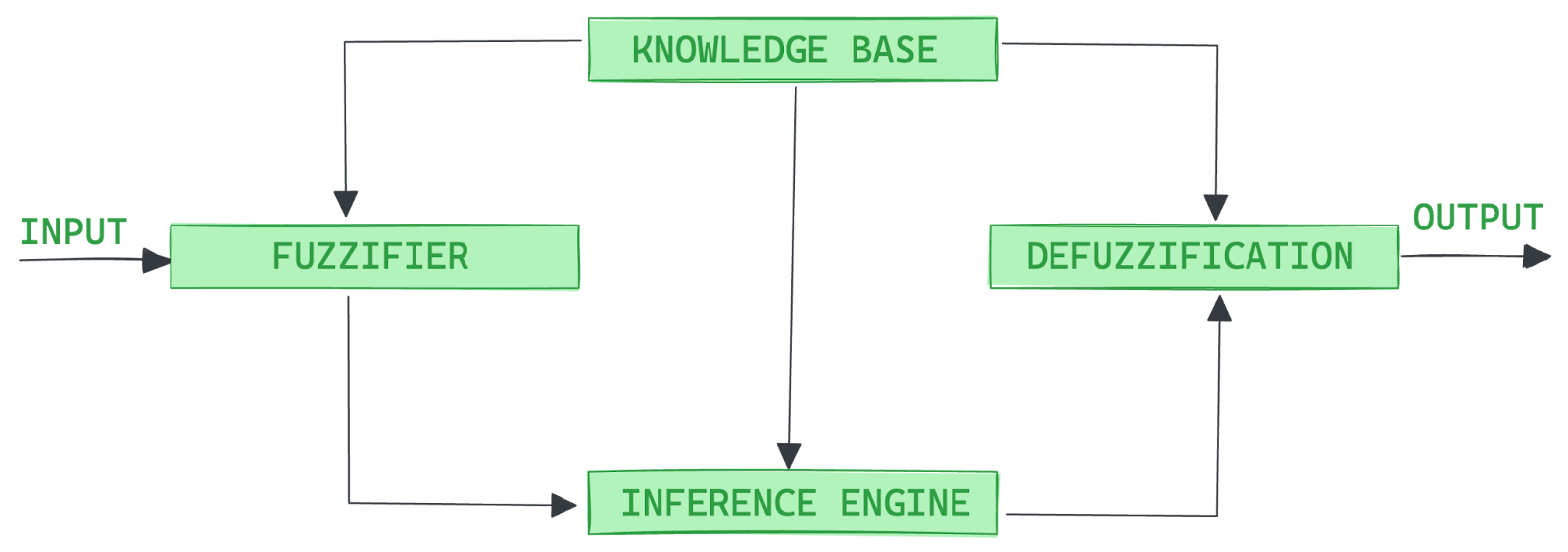
Imagen del autor

1. Fuzzificación

La fuzzificación convierte las entradas crisp -valores precisos medidos por sensores, como la temperatura o la presión- en valores difusos mediante funciones de pertenencia. Estos valores difusos representan grados de pertenencia a distintas categorías (por ejemplo, "frío", "templado" o "caliente"), lo que permite al sistema manejar la imprecisión con eficacia.

2. Base de conocimientos

La base de conocimientos contiene un conjunto de reglas IF-THEN y funciones de pertenencia proporcionadas por expertos. Estas reglas rigen el proceso de toma de decisiones traduciendo las entradas lingüísticas en salidas procesables. Los avances en el diseño de la lógica difusa han agilizado el desarrollo y el ajuste de los controladores difusos, reduciendo a menudo el número de reglas necesarias para un funcionamiento eficaz.

3. Motor de inferencia

El motor de inferencia emula el razonamiento humano evaluando el grado de coincidencia entre las entradas difusas y las reglas almacenadas en la base de conocimientos. Basándose en esta evaluación, determina qué reglas activar y combina sus resultados para formar acciones de control. Este proceso es el núcleo de la toma de decisiones en un sistema de lógica difusa.

4. Desfuzzificación

La defuzzificación transforma la salida difusa generada por el motor de inferencia en un valor crujiente. Este paso traduce las acciones de control difuso en salidas precisas y procesables, adecuadas para las aplicaciones del mundo real. Existen varias técnicas de defuzzificación, y la elección del método depende de los requisitos específicos del sistema.

Al integrar la fuzzificación, una base de conocimiento robusta, un motor de inferencia y la defuzzificación, la arquitectura de un sistema de lógica difusa proporciona un marco potente para manejar la incertidumbre y la complejidad en los procesos de toma de decisiones.

Implementación de la Lógica Difusa en Sistemas de Inteligencia Artificial: Guía paso a paso

Implementar la lógica difusa en los sistemas de IA implica varios pasos estructurados para permitir una mejor toma de decisiones en entornos complejos. Utilizaremos como ejemplo un sencillo sistema automático de aire acondicionado. 

Aquí tienes una guía concisa del proceso:

1. Definir variables y términos lingüísticos

Identifica las variables de entrada y salida relevantes para el sistema, y descríbelas utilizando términos lingüísticos. Para nuestro caso, tendremos: 

Entradas:

• Temperatura: "Bajo", "Medio", "Alto"
• Humedad: "Bajo", "Medio", "Alto"

Salida:

• Velocidad del ventilador: "Bajo", "Medio", "Alto"

Estos términos lingüísticos definen la gama de condiciones de entrada y las acciones de salida deseadas.

2. Construye funciones de pertenencia

Desarrolla funciones de pertenencia para cada término lingüístico con el fin de cuantificar el grado en que una entrada concreta (de temperatura y humedad en nuestro caso) pertenece a un conjunto difuso. Estas funciones asignan valores de entrada a un rango entre 0 y 1, indicando una pertenencia parcial.

3. Formular reglas difusas 

Desarrolla un conjunto de reglas SI-ENTONCES para captar la relación entre las entradas y la salida deseada. Estas reglas simulan la toma de decisiones en condiciones variables.

Reglas de ejemplo para el sistema de aire acondicionado:

1. SI la temperatura es alta Y la humedad es alta, ENTONCES la velocidad del ventilador es alta.
2. SI la temperatura es media Y la humedad es alta, ENTONCES la velocidad del ventilador es media.
3. SI la temperatura es baja Y la humedad es baja, ENTONCES la velocidad del ventilador es baja.

4. Desarrollar el motor de inferencia

Implementa un motor de inferencia para evaluar las reglas difusas en función de los valores de entrada actuales. El motor determina qué reglas se aplican y combina sus resultados para formar una conclusión difusa.

Ejemplo:

• Valores de entrada: Temperatura = 32°C (pertenencia parcial a "Media" y "Alta"), Humedad = 75% (pertenencia parcial a "Media" y "Alta").
• Normas aplicables:
• Regla 1: Verdad parcial debido a la alta temperatura y la alta humedad.
• Regla 2: Verdad parcial por temperatura media y humedad alta.

El motor agrega estas verdades parciales para formar una salida difusa.

5. Ejecuta la defuzzificación

Convierte la salida difusa en un valor crisp para un control accionable. Utiliza métodos de defuzzificación comoel método del centroide para calcular el resultado final.

Ejemplo:

• Salida difusa agregada: Una combinación de velocidades de ventilador "Media" y "Alta" basada en la activación de la regla.
• Salida defuzzificada: Calcula el centroide de la salida agregada, dando como resultado un valor específico de velocidad del ventilador (por ejemplo, 70% de la velocidad máxima).

Siguiendo estos pasos, los sistemas de IA pueden incorporar eficazmente la lógica difusa para manejar la incertidumbre y tomar decisiones similares a las humanas en diversas aplicaciones. Para mejorar tu comprensión y ver más ejemplos de implementación de la lógica difusa, consulta este completo tutorial sobre comparación de cadenas difusas en Python de DataCamp.

Ejemplo Python de lógica difusa

Ahora vamos a realizar un ejemplo práctico utilizando Python. Para ello, primero tienes que instalar la biblioteca scikit-fuzzy. 

! pip install scikit-fuzzy

A continuación, generaremos el código Python correspondiente.

1. Importa las bibliotecas necesarias

Importamos las bibliotecas necesarias para realizar nuestro código en Python. 

import numpy as np
import skfuzzy as fuzz
from skfuzzy import control as ctrl

2. Definir variables lingüísticas (entradas y salidas)

Aquí, definimos las entradas (temperatura y humedad) y la salida (velocidad_del_ventilador) como variables difusas. Cada variable tiene un rango específico de valores, que representan las posibles medidas del mundo real.

temperature = ctrl.Antecedent(np.arange(15, 41, 1), 'temperature')
humidity = ctrl.Antecedent(np.arange(0, 101, 1), 'humidity')
fan_speed = ctrl.Consequent(np.arange(0, 101, 1), 'fan_speed')

3. Funciones de pertenencia 

Las funciones de pertenencia definen el grado en que un valor concreto (por ejemplo, la temperatura o la humedad) pertenece a categorías como "bajo", "medio" o "alto". Se representan como funciones triangulares (trimf ) para simplificar.

# For temperature
temperature['low'] = fuzz.trimf(temperature.universe, [15, 15, 25])
temperature['medium'] = fuzz.trimf(temperature.universe, [20, 25, 30])
temperature['high'] = fuzz.trimf(temperature.universe, [25, 40, 40])

# For humidity
humidity['low'] = fuzz.trimf(humidity.universe, [0, 0, 50])
humidity['medium'] = fuzz.trimf(humidity.universe, [25, 50, 75])
humidity['high'] = fuzz.trimf(humidity.universe, [50, 100, 100])

# For the speed of the fan
fan_speed['low'] = fuzz.trimf(fan_speed.universe, [0, 0, 50])
fan_speed['medium'] = fuzz.trimf(fan_speed.universe, [25, 50, 75])
fan_speed['high'] = fuzz.trimf(fan_speed.universe, [50, 100, 100])

4. Definir reglas difusas

Las reglas establecen relaciones entre entradas y salidas. Por ejemplo:

• Regla 1: Si tanto la temperatura como la humedad son altas, la velocidad del ventilador también debe ser alta.

Estas reglas guían el proceso de toma de decisiones en el sistema.

rule1 = ctrl.Rule(temperature['high'] & humidity['high'], fan_speed['high'])
rule2 = ctrl.Rule(temperature['medium'] & humidity['high'], fan_speed['medium'])
rule3 = ctrl.Rule(temperature['low'] & humidity['low'], fan_speed['low'])

5. Sistema de control

El Sistema de Control compila las reglas difusas en un modelo de trabajo. Lapágina SimulaciónSistemaControl nos permite simular el sistema con unos valores de entrada determinados.

fan_ctrl = ctrl.ControlSystem([rule1, rule2, rule3])
fan_simulation = ctrl.ControlSystemSimulation(fan_ctrl)

6. Introducir valores y realizar el cálculo

Aquí se proporcionan valores de entrada específicos (por ejemplo, 32°C para la temperatura y 75% para la humedad). El sistema procesa estas entradas utilizando las reglas difusas y calcula la velocidad del ventilador correspondiente.

# Input values
fan_simulation.input['temperature'] = 32  # Example temperature (°C)
fan_simulation.input['humidity'] = 75    # Example humidity (%)

# Perform computation
fan_simulation.compute()

El sistema emite un valor crujiente para la velocidad del ventilador basado en el cálculo de lógica difusa. Por ejemplo:

Fan Speed: 78.33%

Aplicaciones de la lógica difusa en la IA

Como probablemente puedas imaginar, hay bastantes casos en los que la lógica difusa puede mejorar los sistemas en el mundo real. He aquí algunos ejemplos: 

Electrónica de consumo

La lógica difusa optimiza el rendimiento de los aparatos gestionando la incertidumbre y las condiciones variables. Por ejemplo, las lavadoras ajustan los ciclos en función del tamaño de la carga, y los aparatos de aire acondicionado regulan eficazmente la temperatura y la velocidad del ventilador.

Sistemas de automoción

La lógica difusa mejora los sistemas de vehículos para un control inteligente. Un buen ejemplo es cómolo utilizan las cajas de cambios automáticas para determinar los cambios de marcha óptimos en función de la velocidad y el acelerador, mientras que el control de crucero adaptativo y los sistemas de gestión del entorno se basan en él para realizar ajustes en tiempo real.

Sanidad

La IA se utiliza ampliamente en la asistencia sanitariay la lógica difusa ayuda al diagnóstico y la monitorización médicos al abordar la variabilidad de la salud humana. Por ejemplo, los sistemas de diagnóstico analizan los síntomas y los resultados de las pruebas para proporcionar diagnósticos probabilísticos, mientras que los sistemas de monitorización de pacientes realizan un seguimiento de las constantes vitales para detectar anomalías.

Automatización industrial

La lógica difusa gestiona procesos industriales complejos para garantizar la fiabilidad. Podemos encontrarlo en la fabricación de productos químicos, donde los controladores difusos regulan la temperatura y la presión en los reactores para conseguir una calidad constante.

Robótica

La lógica difusa permite a los robots navegar por entornos inciertos con eficacia. Seguro que conoces losrobots autónomos de que utilizan esta lógica difusa para la planificación de trayectorias en tiempo real y la evitación de obstáculos, garantizando un movimiento seguro y eficaz .

La capacidad de la lógica difusa para manejar la incertidumbre y adaptarse a condiciones dinámicas la hace indispensable en diversas aplicaciones de IA.

Ventajas y limitaciones de la lógica difusa

Como hemos visto, la lógica difusa es una herramienta versátil y poderosa de la inteligencia artificial, que ofrece soluciones a problemas complejos imitando el razonamiento humano. Sin embargo, como cualquier enfoque, tiene sus puntos fuertes y sus puntos débiles. Comprenderlas puede ayudar a aprovechar sus ventajas y a afrontar sus retos.

Ventajas

• Maneja datos imprecisos: La lógica difusa puede trabajar eficazmente con entradas imprecisas, ruidosas o distorsionadas, lo que la hace muy adaptable.
• Facilidad de comprensión y aplicación: Es fácil de construir y se basa en conceptos matemáticos sencillos de la teoría de conjuntos, por lo que es accesible de aplicar y comprender.
• Razonamiento similar al humano: Al imitar los procesos humanos de toma de decisiones, la lógica difusa ofrece soluciones eficaces a problemas complejos del mundo real.
• Requiere pocos recursos: Los algoritmos de lógica difusa requieren un mínimo de datos y memoria, por lo que consumen pocos recursos.

Limitaciones

• Falta de diseño sistemático: No existe un enfoque estandarizado para resolver problemas utilizando la lógica difusa, lo que puede dar lugar a ambigüedad e incoherencia.
• Dificultad de validación: Demostrar las características y la eficacia de los sistemas de lógica difusa puede ser un reto debido a la ausencia de descripciones matemáticas precisas en muchos casos.
• Posible compromiso de precisión: Aunque maneja bien los datos imprecisos, la lógica difusa a veces puede comprometer el logro de una gran precisión.

La capacidad de la lógica difusa para manejar la incertidumbre y la complejidad es uno de sus principales puntos fuertes, pero sus limitaciones ponen de manifiesto la necesidad de una aplicación y un diseño cuidadosos para garantizar su eficacia.

Conclusión

La lógica difusa permite a los sistemas manejar la incertidumbre e imitar el razonamiento humano. Su flexibilidad y capacidad para procesar datos imprecisos lo hacen necesario en diversas aplicaciones, desde la electrónica de consumo a la robótica y la sanidad.

Con su arquitectura robusta y su facilidad de aplicación, la lógica difusa ofrece soluciones eficaces para problemas complejos. Aunque existen retos como la falta de un diseño sistemático y las posibles compensaciones por la precisión, sus puntos fuertes superan con creces sus limitaciones.

El papel de la lógica difusa como puente entre el razonamiento similar al humano y la precisión computacional garantiza su continua relevancia en el avance de las tecnologías de IA. Si eres totalmente nuevo en el campo de la IA, puedes empezar con el curso de DataCamp Fundamentos de la IA de DataCamp. Para los usuarios más avanzados, otros buenos recursos para mejorar sus habilidades con la IA son: 

• Curso de Desarrollo de Aplicaciones de IA
• Desarrollar sistemas de IA con la API OpenAI