Tutorial sobre la curva de precisión-recuperación en Python

Los algoritmos de aprendizaje automático (AM) se utilizan cada vez más para automatizar tareas mundanas e identificar patrones ocultos en los datos. Pero son inherentemente probabilísticos, lo que significa que sus predicciones no siempre son correctas. Por lo tanto, necesitas una forma de estimar la validez de tu modelo ML para establecer la confianza en tales sistemas. 

Métricas de evaluación como la exactitud, la precisión, el recuerdo, el error cuadrático medio (MSE), el error porcentual absoluto medio (MAPE) y similares se utilizan habitualmente para medir el rendimiento del modelo. Las diferentes métricas te ayudan a medir el rendimiento a través de diferentes criterios y lentes. 

Estas métricas también garantizan que el modelo mejora constantemente en el aprendizaje de su tarea. Al fin y al cabo, si no puedes medir, no puedes mejorar el rendimiento del sistema de ML.

La precisión es una de esas métricas que es fácil de entender y funciona bien con un conjunto de datos equilibrado, es decir, aquél en el que todas las clases tienen la misma representación. Sin embargo, los fenómenos del mundo real no se distribuyen por igual; de ahí que sea difícil encontrar conjuntos de datos tan equilibrados. La precisión consiste principalmente en averiguar si la mayoría de las instancias se identifican correctamente, independientemente de la clase a la que pertenezcan. En el caso de sucesos raros importantes, como una transacción fraudulenta o un clic en una impresión publicitaria, la precisión falsea un modelo que sólo predice todo como la clase negativa, es decir, ningún fraude o ningún clic. Debido a estas limitaciones, la precisión no es la métrica más adecuada. Entonces, ¿qué métrica deberíamos utilizar en su lugar para medir el rendimiento de nuestros modelos?

La precisión y la recuperación son métricas muy utilizadas para evaluar el rendimiento de un modelo de clasificación desequilibrado, como la predicción de la pérdida de clientes. 

Explicación de la precisión y la recuperación

La precisión se refiere a la confianza con la que se predice como positiva una clase positiva, mientras que la recuperación mide lo bien que el modelo identifica el número de instancias de clase positivas del conjunto de datos. Observa que la clase positiva es la clase de interés.

Desde un punto de vista empírico, la precisión y el recuerdo se comprenden mejor con la ayuda de una matriz de confusión que consta de cuatro términos clave:

• Verdadero positivo (TP): Número de casos de clase positiva correctamente identificados
• Falso positivo (FP): Número de casos de clase negativa identificados erróneamente como casos de clase positiva
• Verdadero negativo (VN): Número de casos de clase negativa correctamente identificados
• Falso negativo (FN): Número de casos de clase positiva identificados erróneamente como casos de clase negativa

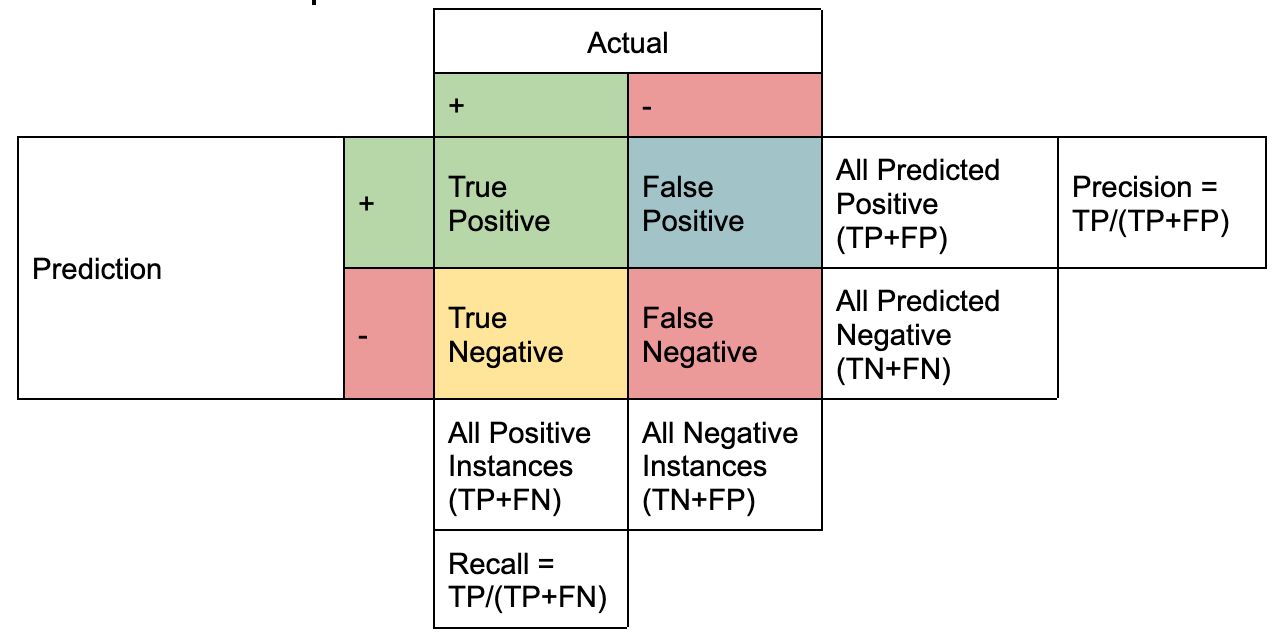
Representación creada por el Autor

Precisión y Recall son una expresión matemática de estos cuatro términos donde:

La precisión es la proporción de TP respecto a todos los casos de predicciones positivas (TP+FP). La recuperación es la proporción de TP de todas las instancias positivas (TP+FN).

Se simplifica aún más utilizando la siguiente notación que destaca la diferencia entre ambas. Esencialmente, ambas métricas tienen el mismo numerador, que es la intersección de las instancias positivas reales con la de las instancias predichas positivamente, es decir, TP.

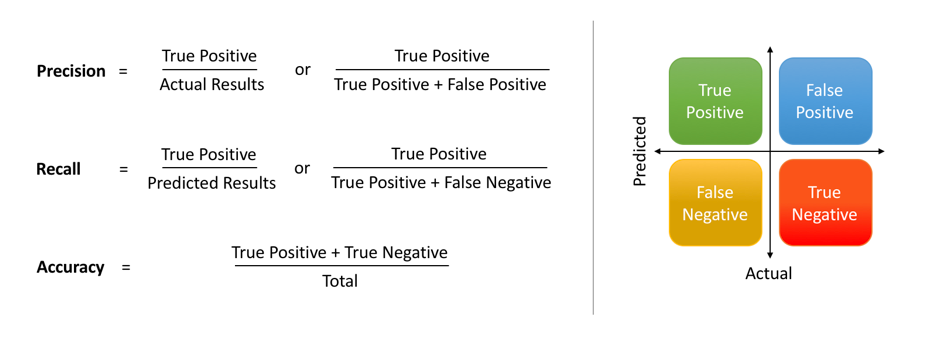
Imagen de Shruti Saxena

El diferenciador está en el denominador, donde la Precisión considera todas las instancias predichas positivamente (TP+FP), frente a las instancias positivas reales (TP+FN) en el caso de la Recuperación. 

La intuición tras la precisión y la recuperación 

Hay una razón por la que la matriz de confusión se llama así: es realmente confusa cuando intentas comprender estos conceptos por primera vez. 

Así pues, interioricemos el concepto con la ayuda de un ejemplo. Supongamos que tienes una planta siderúrgica en la que la fábrica extrae hierro del mineral de hierro y lo mezcla con otros minerales y elementos (a veces involuntariamente). Centrándonos en la parte de la extracción, tienes algunas opciones en cuanto a la pureza del metal extraído y los residuos producidos durante el proceso, como se indica a continuación:

Supuesto 1: Sólo quieres dar prioridad a la pureza del hierro extraído, independientemente de cuánto metal se desperdicie en el proceso.

Supuesto 2: Quieres maximizar la eficacia, es decir, la cantidad de hierro extraída por unidad de mineral, sin tener en cuenta la pureza del metal extraído.

Escenario 3: Quieres lo mejor de ambos mundos, es decir, mantener la pureza del metal extraído lo más alta posible y reducir al mismo tiempo los residuos (maximizar el hierro extraído por unidad de mineral).

Piensa en el alto horno o en el horno de arco eléctrico como opciones de modelado que proporcionan resultados diferentes (pureza del mineral de hierro y residuos). Digamos que uno de los métodos de extracción proporciona un 97,5% de hierro puro y pierde un 4% del hierro en los lodos. Así, podemos definir nuestra precisión como la fracción de hierro puro en el metal extraído, es decir, el 97,5%, mientras que la recuperación es la cantidad de hierro extraído de todo el hierro disponible en el mineral, que es el 96% (se desperdicia el 4% de todo el hierro).

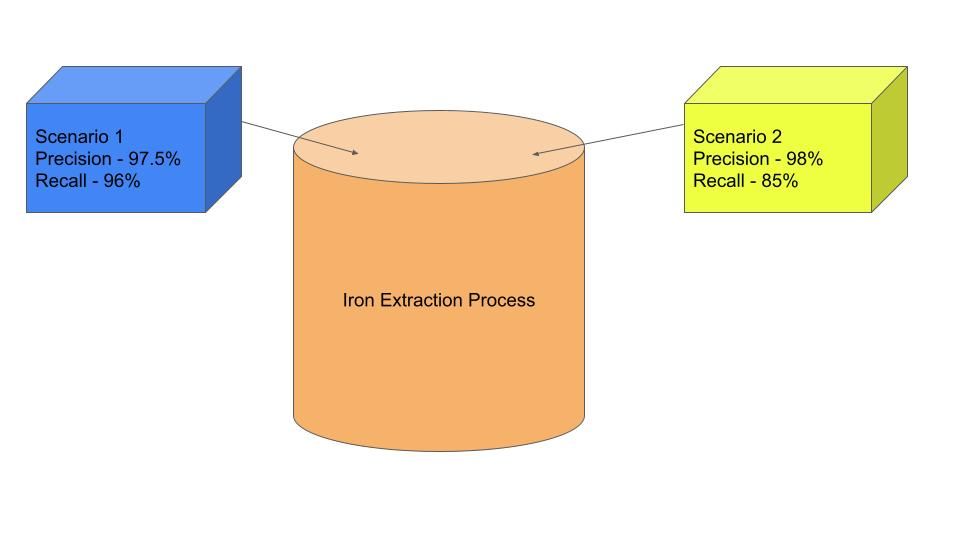
Ilustración creada por el Autor

Digamos que sigues el segundo método porque quieres obtener hierro más puro del horno, lo que a su vez implica más residuos en el proceso de extracción. Supongamos que si aumentas la pureza del hierro en un 0,5% hasta el 98%, tus residuos de metal aumentan en un 11%. Esto significa que el valor de recuerdo correspondiente a un valor de precisión del 98% pasa a ser del 85%. Este trueque del recuerdo a cambio de una mayor precisión y viceversa muestra la relación inversa de precisión y recuerdo.

¿No sería estupendo que pudieras conocer todos los valores de precisión y los correspondientes valores de recuerdo para poder tomar la decisión que mejor se adapte a tu objetivo?

La curva de precisión-recuerdo ayuda a hacer esa elección, y lo entenderás en profundidad en los siguientes apartados. Pero antes de hacerlo, entendamos primero un concepto importante del umbral que es fundamental para la curva de RP. 

El concepto de umbral

Pongamos un ejemplo de identificación de transacciones fraudulentas para entender cómo funciona un umbral (o límite). La tabla siguiente tiene cuatro transacciones con identificadores de transacción que van de 1 a 4; una transacción puede ser fraudulenta o regular. El modelo de detección del fraude da la probabilidad de que una transacción sea fraudulenta (resaltada en la columna amarilla), lo que intrínsecamente delata la probabilidad de una transacción regular. 

Se dice que una transacción se predice como fraudulenta si la probabilidad de salida es mayor que el umbral elegido en la columna Probabilidad de transacción fraudulenta, de lo contrario se declara como transacción normal. 

Cuando se aplica un umbral tan estricto como 0,9, las tres primeras transacciones se marcan como regulares, mientras que la última se marca como transacción fraudulenta. Un umbral tan alto destila confianza en las predicciones, lo que conduce a un escenario de alta precisión. A cambio, sacrificas la retirada del modelo al perderte algunas transacciones fraudulentas.

Este escenario no es deseable a pesar de la elevada Precisión. ¿Se te ocurre por qué?

Esto se debe a que la empresa acaba pagando un coste más elevado por no poder identificar el fraude, que es el único objetivo de construir un modelo de este tipo. Ten en cuenta que el coste de una transacción fraudulenta es mucho mayor que el de las transacciones bloqueadas pero regulares, es decir, FP. 

Ahora, considera el otro lado del espectro con un valor umbral bajo de 0,4 que marca las tres transacciones inferiores como fraudulentas. Un umbral tan liberal bloqueará la mayoría de las transacciones, lo que puede molestar a muchos clientes. Sin olvidar la carga adicional que supone para los recursos humanos analizar las transacciones marcadas e identificar los verdaderos fraudes.

Por tanto, la empresa tiene que definir las métricas objetivo y sus valores deseados para obtener lo mejor de ambos mundos, teniendo en cuenta los siguientes costes:

• El coste de identificar una transacción fraudulenta como regular (Falsos Negativos)
• El coste de identificar una transacción regular como fraudulenta (Falso Positivo)

Volviendo a la definición de precisión, verías que los falsos positivos están en el denominador de la expresión matemática, lo que significa que minimizar los falsos positivos maximizaría la precisión. Del mismo modo, minimizar los falsos negativos maximizaría el recuerdo del modelo.

Por tanto, que una transacción se prediga como fraudulenta o regular depende en gran medida del valor umbral.

¿Qué es una Curva de Precisión-Recuperación?

Una curva de precisión-recuperación te ayuda a decidir un umbral en función de los valores deseables de precisión y recuperación. También resulta útil para comparar el rendimiento de distintos modelos calculando el "Área bajo la curva de precisión-recobro", abreviada como AUC.

Como se explica mediante la matriz de confusión, un modelo de clasificación binaria dará TP, FP, TN y FN para varios valores de umbral, donde cada valor de umbral da como resultado el par correspondiente de valores de precisión y recuperación. 

Si se trazan los valores de recuerdo en el eje x y los valores de precisión correspondientes en el eje y, se genera una curva PR que ilustra una función de pendiente negativa. Representa el compromiso entre precisión (reducción de FPs) y recall (reducción de FNs) para un modelo determinado. Teniendo en cuenta la relación inversa entre precisión y recuperación, la curva suele ser no lineal, lo que implica que al aumentar una métrica disminuye la otra, pero la disminución puede no ser proporcional.

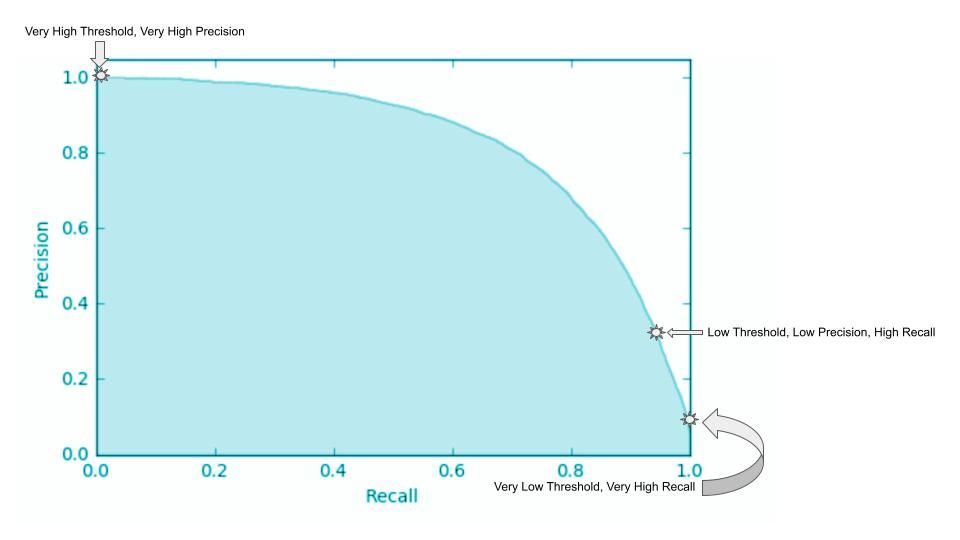
Imagen de StackExchange

Supongamos que una organización elige un valor de recuerdo mínimo aceptable del 98%. La precisión se sitúa en el 30% en un punto de cruce representado por la estrella etiquetada como "Umbral bajo, Precisión baja, Recuperación alta".  

Los otros dos puntos extremos representan los casos en los que el umbral es:

• Demasiado bajo conduce a un alto Recall: el coste del capital humano y de los clientes molestos
• Demasiado alto conlleva una gran Precisión: el coste de las transacciones fraudulentas y la pérdida de reputación.

Utilizar una curva PR

Además de decidir el punto de corte adecuado alineado con la métrica empresarial, se puede utilizar el área bajo la curva de las curvas de precisión-recuerdo de múltiples modelos o algoritmos para comparar su rendimiento. Resulta especialmente útil comparar modelos utilizando curvas PR en lugar de utilizar la precisión individual, la recuperación o incluso una métrica de puntuación F1 (que es una media armónica de la Precisión y la Recuperación).

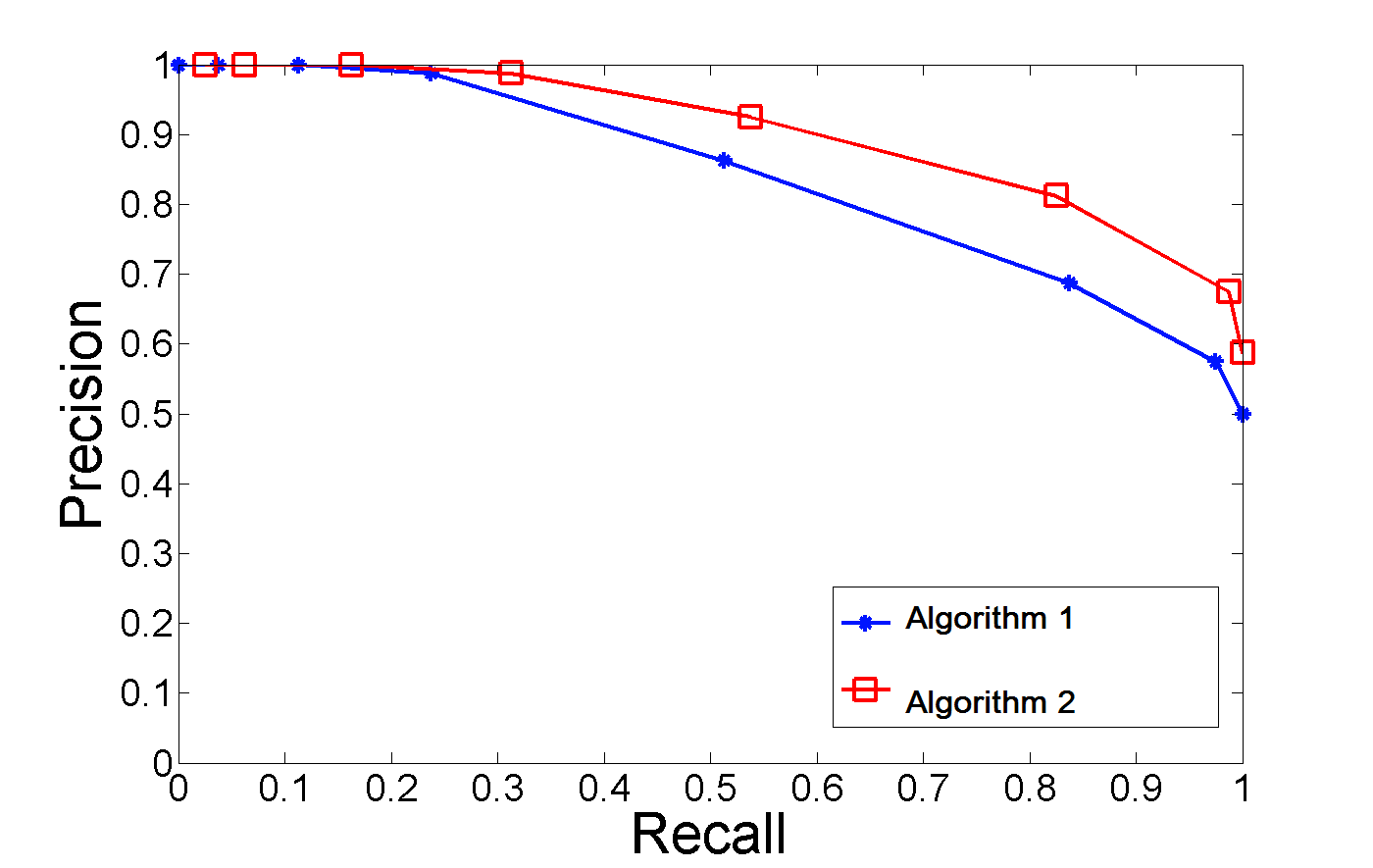
Imagen de Stackoverflow

Estas métricas dependen del umbral, por lo que un cambio en el umbral modifica la distribución de TP, FP y FN. Dos modelos distintos pueden funcionar de forma diferente para un umbral determinado, lo que hace que la curva PR sea una opción sólida para la comparación de modelos. El gráfico anterior ilustra dos curvas PR de dos algoritmos diferentes en un conjunto de datos determinado: el AUC del algoritmo dos es mayor que el AUC del algoritmo uno, lo que lo convierte en la mejor opción para el problema en cuestión.

Implementación de la curva Precision-Recall en Python

Ahora que sabemos qué son las curvas de precisión-recordatorio y para qué se utilizan, vamos a ver cómo crear una curva de precisión-recordatorio en Python. 

Paso 1: Importa los paquetes Python necesarios

Veamos el conjunto de datos modelo para la detección del cáncer de mama, donde la "clase 1" representa el diagnóstico de cáncer y la "clase 0" representa que no hay cáncer.

La primera importación carga el conjunto de datos de "sklearn.datasets", que incluye las variables independientes y las variables objetivo. Como se trata de un conjunto de datos modelo que pueden aprender fácilmente la mayoría de los algoritmos, hemos elegido el algoritmo Naive Bayes importado como "GaussianNB" de sklearn. 

La siguiente importación de "Precision_Recall_curve" da como resultado diferentes umbrales y sus correspondientes valores de Precision y Recall.

from sklearn.datasets import load_breast_cancer
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import precision_recall_curve
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

Paso 2: Preparar los datos de entrenamiento y de prueba

Las variables independientes se almacenan en la clave "datos" y la variable objetivo en la clave "objetivo" dentro del diccionario "datos". A continuación, los datos se dividen en los conjuntos de entrenamiento y prueba pasando el argumento tamaño_prueba con un valor de 0,3.

# Load model breast cancer data
data = load_breast_cancer()
X = data['data']
y = data['target']

Veamos la distribución de la clase positiva y negativa, es decir, los casos de cáncer de mama y los que no lo son.

import numpy as np
unique, counts = np.unique(y, return_counts=True)
plt.pie(counts, labels=unique, autopct='%.0f%%');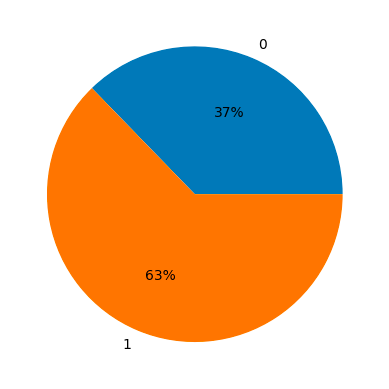

Divide los datos en los conjuntos de entrenamiento y prueba utilizando el método train_test_split del módulo model_selection de sklearn.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

Paso 3: Modelo de formación

Los datos de entrenamiento se analizan como argumentos de GaussianNB() para iniciar el entrenamiento del modelo. A continuación, el objeto modelo ajustado se utiliza para obtener las predicciones en forma de probabilidad sobre el conjunto de datos de entrenamiento y de prueba. 

# Fit a Naive Bayes model
clf = GaussianNB().fit(X_train, y_train)

Paso 4: Generar predicciones

Genera probabilidades de predicción utilizando el conjunto de datos de entrenamiento y de prueba, que se utilizarán para obtener Precisión y Recall con distintos valores del umbral.

# Predict probability
y_prob_train = clf.predict_proba(X_train)[:,1]
y_prob_test = clf.predict_proba(X_test)[:,1]

Paso 5: Trazado de la curva PR

El método Precision_Recall_curve() toma dos datos de entrada: las probabilidades del conjunto de datos de entrenamiento, es decir, y_prob_train, y los valores reales, y devuelve tres valores: Precision, Recall y thresholds.

precision, recall, thresholds = precision_recall_curve(y_train, y_prob_train)
plt.fill_between(recall, precision)
plt.ylabel("Precision")
plt.xlabel("Recall")
plt.title("Train Precision-Recall curve");

Los vectores de precisión y recuperación se utilizan para trazar la curva PR con distintos umbrales, como se muestra a continuación:

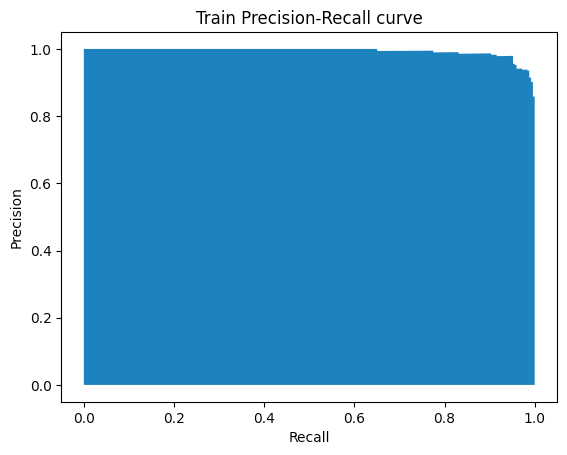
Curva PR generada por el Autor

¿Es mejor una curva Precisión-Recuperación que una curva ROC?

Una curva ROC es similar a la curva PR, pero traza la Tasa de Verdaderos Positivos (TPR) frente a la Tasa de Falsos Positivos (FPR) para diferentes umbrales. Ya conocemos la RPT, es sólo otro nombre para la retirada. Por tanto, centrémonos en el FPR, que significa el número de clasificaciones erróneas de la clase negativa. Siguiendo con el ejemplo del fraude, representa el porcentaje de transacciones regulares marcadas como fraudulentas.

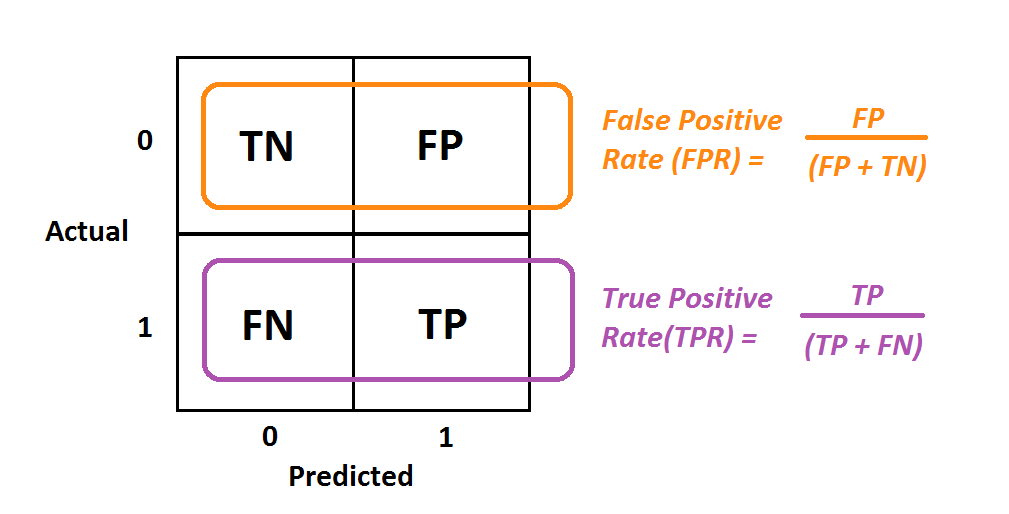
Imagen de Albert Um

A estas alturas, ya sabemos que el recuerdo, también conocido como TPR, es común entre la curva PR y la curva ROC; la principal diferencia es la precisión y el FPR respectivamente. Veamos por qué una curva PR es comparativamente más informativa.

Esto se debe a que la curva P-R proporciona información más significativa sobre la clase de interés que la curva ROC. Elijamos la predicción de transacción fraudulenta. Los Verdaderos Negativos (NT) en casos de conjuntos de datos desequilibrados tienden a ser muy grandes, lo que hace que FPR sea un valor muy pequeño. Pero, ¿dice eso algo sobre el rendimiento del modelo a la hora de predecir una transacción como fraudulenta?

¡No! Por otra parte, utilizar la Precisión como una de las métricas describe el rendimiento del modelo en la clase positiva (transacciones fraudulentas). Describe si el modelo es conservador o liberal a la hora de marcar las transacciones fraudulentas.

El segundo gran inconveniente de la curva ROC es su inmunidad a los datos desequilibrados. En la figura anterior, puedes ver que FP es una métrica sólo de clase negativa, lo que significa que se espera que el cambio en FP sea proporcional al cambio en FP+TN (todas las instancias negativas). Por tanto, si cambia la distribución de los datos subyacentes, el ROC no cambia significativamente. Esta insensibilidad a la distribución de clases hace que la curva PR sea mejor que la curva ROC.

Reflexiones finales

La precisión y la recuperación son métricas de evaluación clave para medir el rendimiento de los modelos de clasificación de aprendizaje automático. Sin embargo, la compensación entre ambos depende de la prerrogativa empresarial y se resuelve mejor mediante la curva de relaciones públicas. El artículo explicaba cómo interpretar la curva de relaciones públicas y elegir el umbral adecuado para alcanzar el objetivo empresarial. Además, el post ilustraba un tutorial paso a paso sobre cómo trazarlo utilizando Python. También discutimos por qué la curva PR es más informativa que la curva ROC.