Introducción a los modelos lineales
Practique Lasso y Ridge Regression en Python con este ejercicio práctico.
La regresión lineal es un tipo de modelo lineal que se considera el algoritmo de predicción más básico y utilizado. Esto no puede disociarse de su arquitectura sencilla pero eficaz. Un modelo lineal supone una relación lineal entre la(s) variable(s) de entrada 𝑥 y una variable de salida y. La ecuación de un modelo lineal es la siguiente:
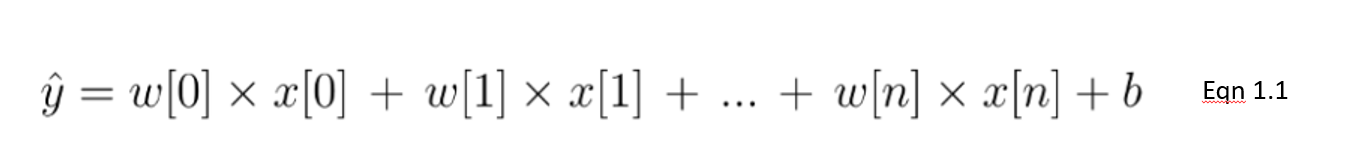
En esta ecuación 1.1, mostramos un modelo lineal con un número n de características. w se considera el coeficiente (o peso) asignado a cada característica, un indicador de su importancia para el resultado y. Por ejemplo, suponemos que la temperatura influye más en las ventas de helados que el hecho de que sea festivo. El peso asignado a la temperatura en nuestro modelo lineal será mayor que el de la variable de días festivos.
El objetivo de un modelo lineal consiste entonces en optimizar el peso (b) mediante la función de coste de la ecuación 1.2. La función de coste calcula el error entre las predicciones y los valores reales, representado como un único número de valor real. La función de coste es el error medio en n muestras del conjunto de datos, representado a continuación como:
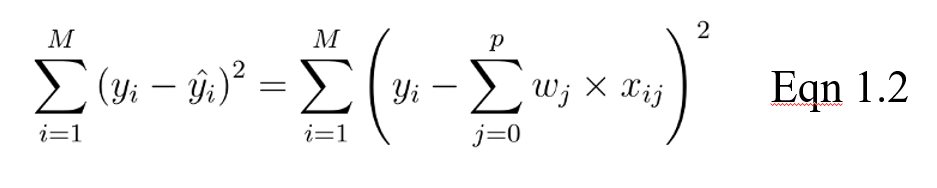
En la ecuación anterior, yi es el valor real y es el valor predicho a partir de nuestra ecuación lineal, donde M es el número de filas y P es el número de características.
Empieza a aprender Python gratis
Intermediate Regression with statsmodels in Python
Regularización
A la hora de entrenar modelos, pueden surgir dos grandes problemas: el sobreajuste y el infraajuste.
- La sobreadaptación se produce cuando el modelo funciona bien en el conjunto de datos de entrenamiento, pero no tan bien en los datos no vistos (de prueba).
- La inadaptación se produce cuando no funciona bien ni en el conjunto de entrenamiento ni en el conjunto de prueba.
En particular, la regularización se aplica para evitar el sobreajuste de los datos, especialmente cuando hay una gran varianza entre el rendimiento del conjunto de entrenamiento y el de prueba. Con la regularización, el número de características utilizadas en el entrenamiento se mantiene constante, pero la magnitud de los coeficientes (w), como se ve en la ecuación 1.1, se reduce.
Considere la siguiente imagen de coeficientes para predecir los precios de la vivienda. Aunque hay bastantes predictores, RM y RAD tienen los mayores coeficientes. La consecuencia será que los precios de la vivienda se verán influidos en mayor medida por estas dos características, lo que provocará un exceso de ajuste y que no se aprendan patrones generalizables.
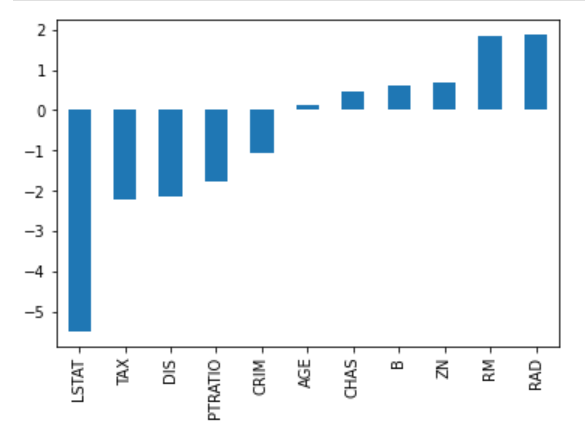
Existen diferentes formas de reducir la complejidad del modelo y evitar el sobreajuste en los modelos lineales. Esto incluye los modelos de regresión ridge y lasso.
Introducción a la regresión Lasso
Se trata de una técnica de regularización utilizada en la selección de características mediante un método de encogimiento también denominado método de regresión penalizada. Lasso es la abreviatura de Least Absolute Shrinkageand Selection Operator, que se utiliza tanto para la regularización como para la selección de modelos. Si un modelo utiliza la técnica de regularización L1, se denomina regresión lasso.
Regresión Lasso para la regularización
En esta técnica de encogimiento, los coeficientes determinados en el modelo lineal de la ecuación 1.1. anterior se encogen hacia el punto central como media introduciendo un factor de penalización denominado valores alfa α (o a veces lamda).
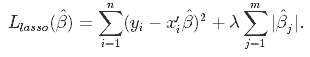
Alfa (α) es el término de penalización que denota la cantidad de contracción (o restricción) que se aplicará en la ecuación. Con alfa ajustado a cero, encontrará que esto es equivalente al modelo de regresión lineal de la ecuación 1.2, y un valor mayor penaliza la función de optimización. Por lo tanto, la regresión lasso reduce los coeficientes y ayuda a reducir la complejidad del modelo y la multicolinealidad.
Alfa (α) puede ser cualquier número de valor real entre cero e infinito; cuanto mayor sea el valor, más agresiva será la penalización.
Regresión Lasso para la selección de modelos
Debido al hecho de que los coeficientes se reducirán hacia una media de cero, las características menos importantes de un conjunto de datos se eliminan cuando se penalizan. La contracción de estos coeficientes basada en el valor alfa proporcionado conduce a algún tipo de selección automática de características, ya que las variables de entrada se eliminan en un enfoque eficaz.
Regresión Ridge
Al igual que la regresión lasso, la regresión ridge impone una restricción similar a los coeficientes mediante la introducción de un factor de penalización. Sin embargo, mientras que la regresión lasso toma la magnitud de los coeficientes, la regresión ridge toma el cuadrado.
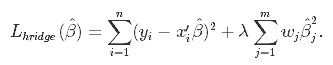
La regresión Ridge también se conoce como Regularización L2.
Por qué Lasso puede utilizarse para la selección de modelos, pero no para la regresión Ridge
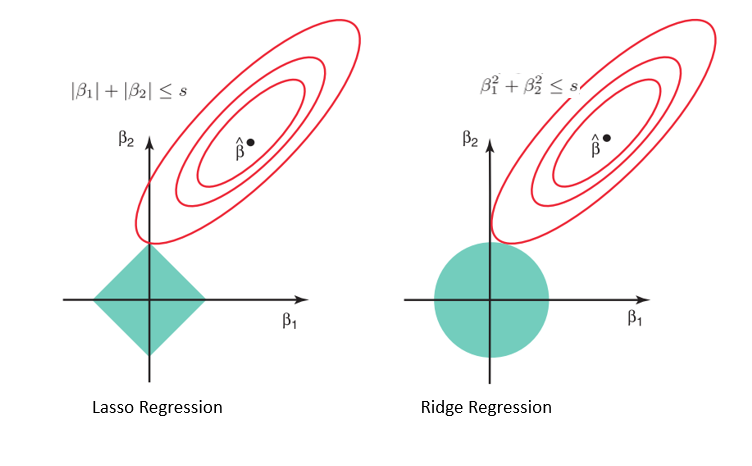
Considerando la geometría de los modelos de lazo (izquierda) y de cresta (derecha), los contornos elípticos (círculos rojos) son las funciones de coste de cada uno. La relajación de las restricciones introducidas por el factor de penalización conduce a un aumento de la región restringida (rombo, círculo). Haciendo esto continuamente, llegaremos al centro de la elipse, donde los resultados de los modelos lasso y ridge son similares a los de un modelo de regresión lineal.
Sin embargo, ambos métodos determinan los coeficientes encontrando el primer punto en el que los contornos elípticos chocan con la región de restricciones. Dado que la regresión lasso adopta una forma de diamante en el gráfico de la región restringida, cada vez que las regiones elípticas se cruzan con estas esquinas, al menos uno de los coeficientes se convierte en cero. Esto es imposible en el modelo de regresión de cresta, ya que tiene forma circular y, por tanto, los valores pueden reducirse cerca de cero, pero nunca ser iguales a cero.
Aplicación de Python
Para esta implementación, utilizaremos el conjunto de datos sobre viviendas de Boston que se encuentra en Sklearn. Lo que pretendemos ver es:
- Cómo realizar regresión ridge y lasso en Python
- Comparar los resultados con un modelo de regresión lineal
Importación de datos y EDA
#libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge, RidgeCV, Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
#data
boston = load_boston()
boston_df=pd.DataFrame(boston.data,columns=boston.feature_names)
#target variable
boston_df['Price']=boston.target
#preview
boston_df.head()
#Exploration
plt.figure(figsize = (10, 10))
sns.heatmap(boston_df.corr(), annot = True)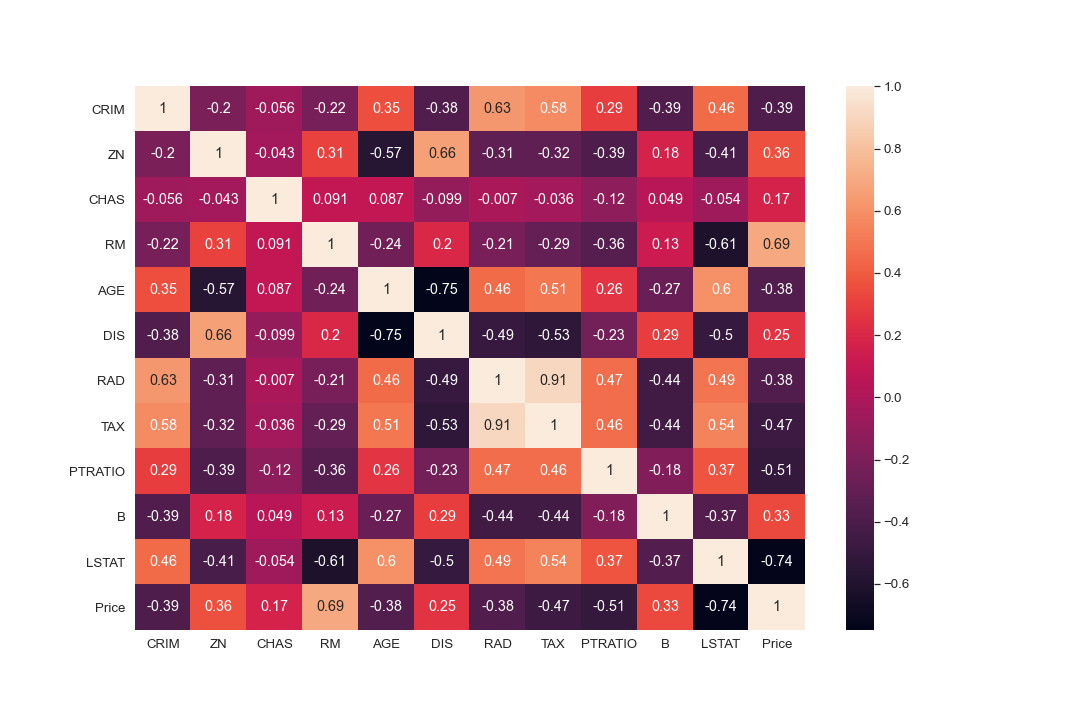
#There are cases of multicolinearity, we will drop a few columns
boston_df.drop(columns = ["INDUS", "NOX"], inplace = True)
#pairplot
sns.pairplot(boston_df)
#we will log the LSTAT Column
boston_df.LSTAT = np.log(boston_df.LSTAT)
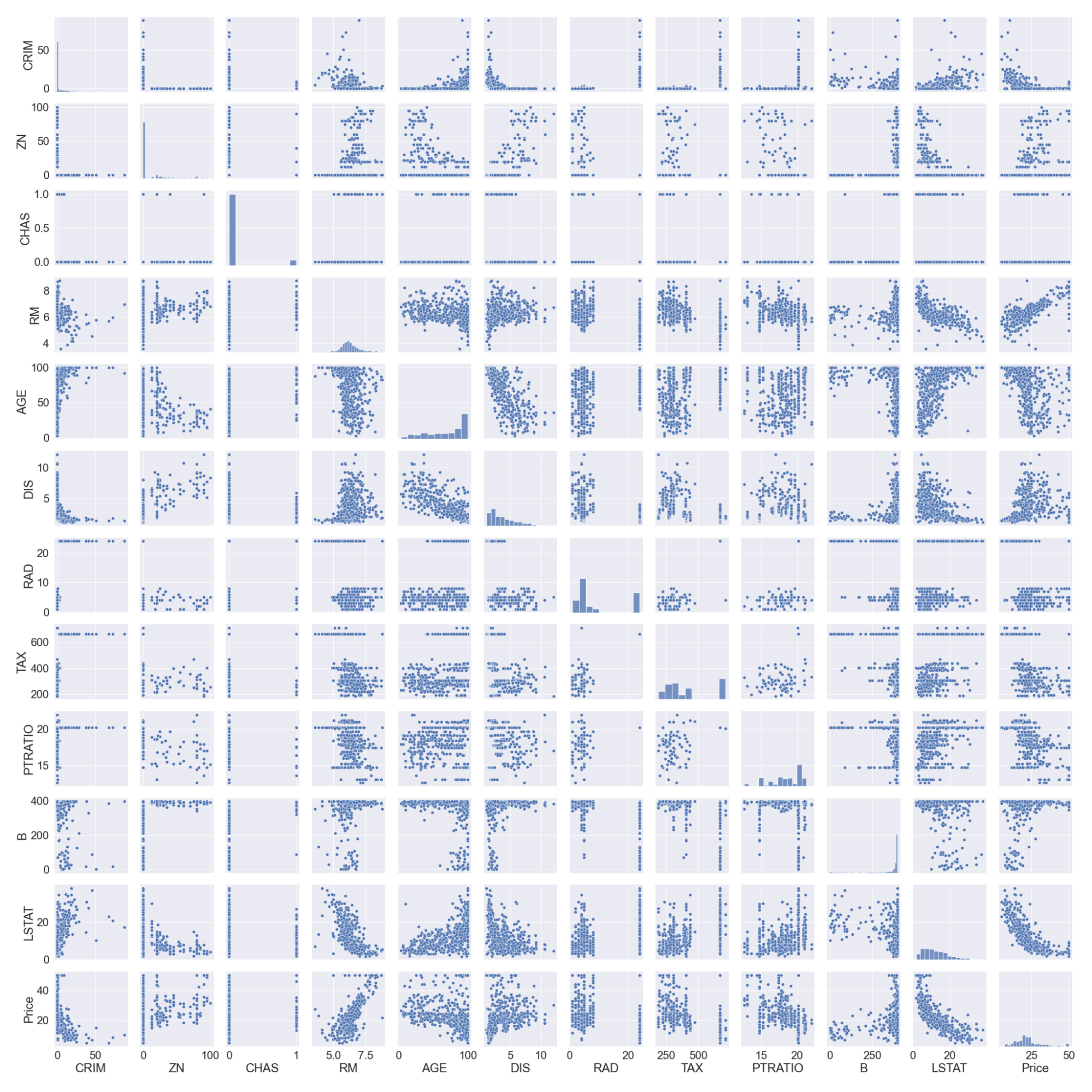
Tenga en cuenta que hemos registrado la columna LSTAT, ya que no tiene una relación lineal con la columna de precios. Los modelos lineales suponen una relación lineal entre las variables x e y.
División y escalado de datos
#preview
features = boston_df.columns[0:11]
target = boston_df.columns[-1]
#X and y values
X = boston_df[features].values
y = boston_df[target].values
#splot
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=17)
print("The dimension of X_train is {}".format(X_train.shape))
print("The dimension of X_test is {}".format(X_test.shape))
#Scale features
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
Salida:

Modelos de regresión lineal y Ridge
Construiremos un modelo de regresión lineal y otro de cresta y luego compararemos los coeficientes en un gráfico. La puntuación de los conjuntos de entrenamiento y prueba también nos ayudará a evaluar el rendimiento del modelo.
#Model
lr = LinearRegression()
#Fit model
lr.fit(X_train, y_train)
#predict
#prediction = lr.predict(X_test)
#actual
actual = y_test
train_score_lr = lr.score(X_train, y_train)
test_score_lr = lr.score(X_test, y_test)
print("The train score for lr model is {}".format(train_score_lr))
print("The test score for lr model is {}".format(test_score_lr))
#Ridge Regression Model
ridgeReg = Ridge(alpha=10)
ridgeReg.fit(X_train,y_train)
#train and test scorefor ridge regression
train_score_ridge = ridgeReg.score(X_train, y_train)
test_score_ridge = ridgeReg.score(X_test, y_test)
print("\nRidge Model............................................\n")
print("The train score for ridge model is {}".format(train_score_ridge))
print("The test score for ridge model is {}".format(test_score_ridge))

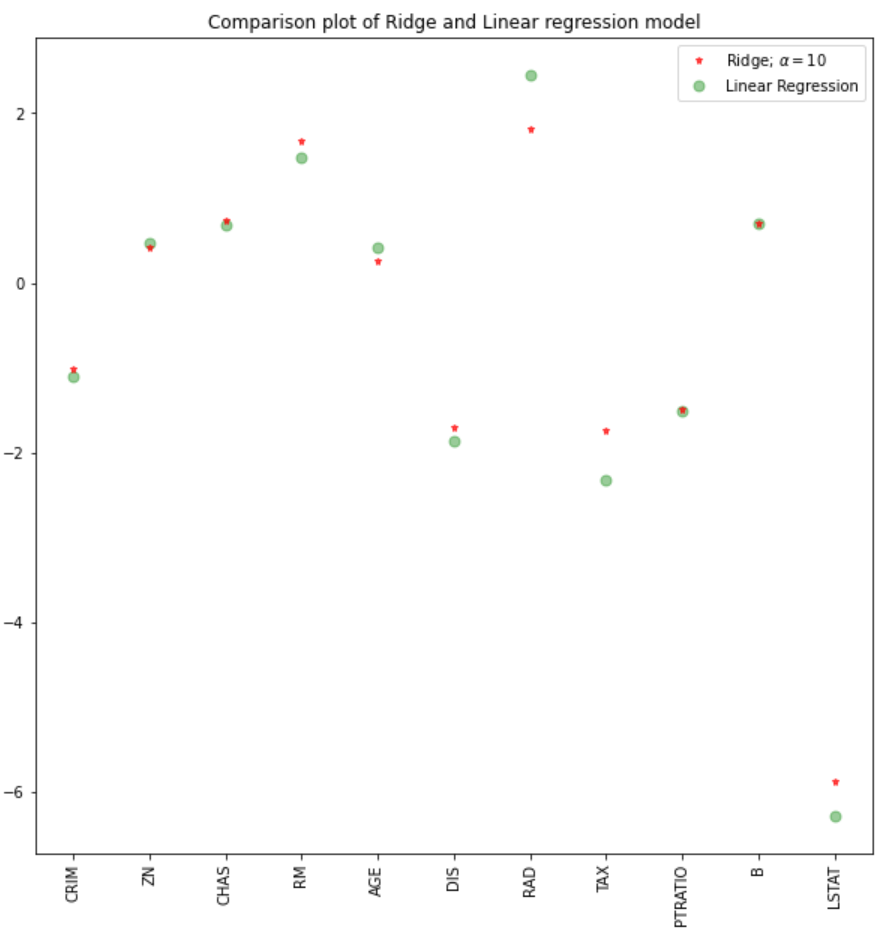
Utilizando un valor alfa de 10, la evaluación del modelo, el tren y los datos de prueba indican un mejor rendimiento del modelo de cresta que del modelo de regresión lineal.
También podemos trazar los coeficientes de los modelos lineal y de cresta.
plt.figure(figsize = (10, 10))
plt.plot(features,ridgeReg.coef_,alpha=0.7,linestyle='none',marker='*',markersize=5,color='red',label=r'Ridge; $\alpha = 10$',zorder=7)
#plt.plot(rr100.coef_,alpha=0.5,linestyle='none',marker='d',markersize=6,color='blue',label=r'Ridge; $\alpha = 100$')
plt.plot(features,lr.coef_,alpha=0.4,linestyle='none',marker='o',markersize=7,color='green',label='Linear Regression')
plt.xticks(rotation = 90)
plt.legend()
plt.show()
Regresión Lasso
#Lasso regression model
print("\nLasso Model............................................\n")
lasso = Lasso(alpha = 10)
lasso.fit(X_train,y_train)
train_score_ls =lasso.score(X_train,y_train)
test_score_ls =lasso.score(X_test,y_test)
print("The train score for ls model is {}".format(train_score_ls))
print("The test score for ls model is {}".format(test_score_ls))

También podemos visualizar los coeficientes.
pd.Series(lasso.coef_, features).sort_values(ascending = True).plot(kind = "bar")
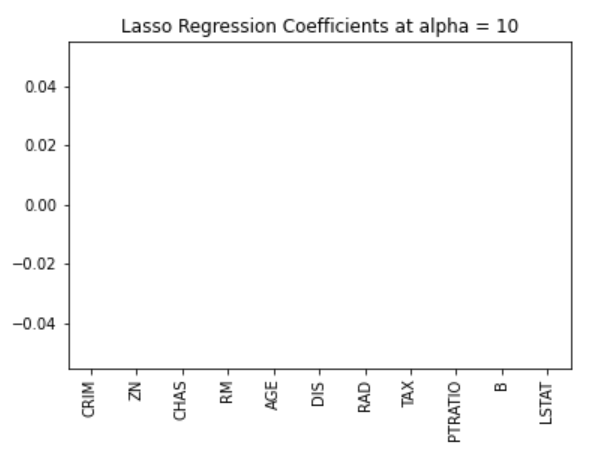
Anteriormente, establecimos que el modelo de lazo puede inerte a cero debido a la forma de diamante de la región de restricción. En este caso, utilizar un valor alfa de 10 penaliza en exceso el modelo y reduce todos los valores a cero. Podemos comprobarlo efectivamente visualizando los coeficientes del modelo como se muestra en la figura anterior.
Selección de valores alfa óptimos mediante validación cruzada en Sklearn
Puede que tengamos que probar diferentes valores de alfa para encontrar el valor óptimo de la restricción. Para este caso, podemos utilizar el modelo de validación cruzada del paquete sklearn. Esto probará diferentes combinaciones de valores alfa y luego elegirá el mejor modelo.
#Using the linear CV model
from sklearn.linear_model import LassoCV
#Lasso Cross validation
lasso_cv = LassoCV(alphas = [0.0001, 0.001,0.01, 0.1, 1, 10], random_state=0).fit(X_train, y_train)
#score
print(lasso_cv.score(X_train, y_train))
print(lasso_cv.score(X_test, y_test))
Salida:

El modelo será entrenado en diferentes valores alfa que he especificado en la función LassoCV. Podemos observar un mejor rendimiento del modelo, eliminando el tedioso esfuerzo de cambiar manualmente los valores alfa.
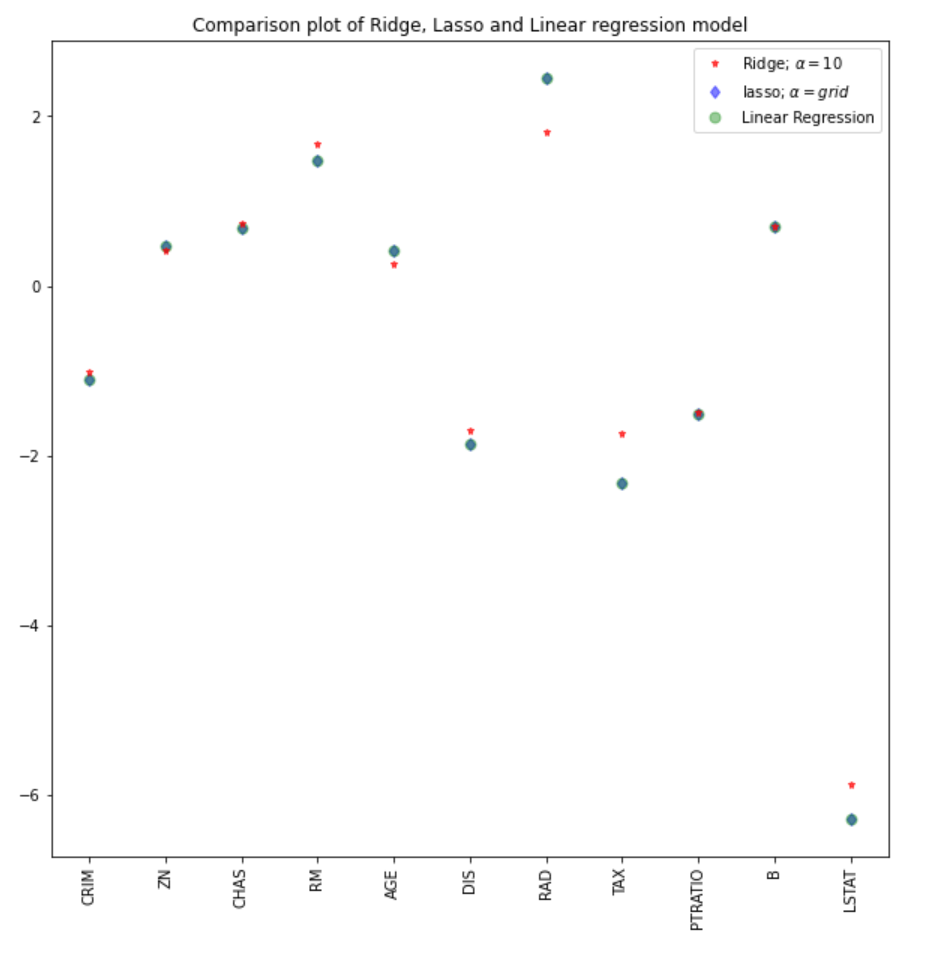
Podemos comparar los coeficientes del modelo lasso con el resto de modelos (lineal y ridge).
#plot size
plt.figure(figsize = (10, 10))
#add plot for ridge regression
plt.plot(features,ridgeReg.coef_,alpha=0.7,linestyle='none',marker='*',markersize=5,color='red',label=r'Ridge; $\alpha = 10$',zorder=7)
#add plot for lasso regression
plt.plot(lasso_cv.coef_,alpha=0.5,linestyle='none',marker='d',markersize=6,color='blue',label=r'lasso; $\alpha = grid$')
#add plot for linear model
plt.plot(features,lr.coef_,alpha=0.4,linestyle='none',marker='o',markersize=7,color='green',label='Linear Regression')
#rotate axis
plt.xticks(rotation = 90)
plt.legend()
plt.title("Comparison plot of Ridge, Lasso and Linear regression model")
plt.show()
Nota: Un enfoque similar podría emplearse para el modelo de regresión ridge, lo que podría conducir a mejores resultados. En el paquete sklearn, la función RidgeCV funciona de forma similar.
#Using the linear CV model from sklearn.linear_model import RidgeCV #Lasso Cross validation ridge_cv = RidgeCV(alphas = [0.0001, 0.001,0.01, 0.1, 1, 10]).fit(X_train, y_train) #score print("The train score for ridge model is {}".format(ridge_cv.score(X_train, y_train))) print("The train score for ridge model is {}".format(ridge_cv.score(X_test, y_test)))
Aprende otros tipos de regresión con nuestros tutoriales de regresión logística en python y regresión lineal en python.
Conclusión
Hemos visto una aplicación de los modelos de regresión ridge y lasso, así como los conceptos teóricos y matemáticos en los que se basan estas técnicas. Algunos de los puntos clave de este tutorial son:
- La función de coste de la regresión ridge y la regresión lasso son similares. Sin embargo, la regresión de cresta toma el cuadrado de los coeficientes y el lazo toma la magnitud.
- La regresión Lasso puede utilizarse para la selección automática de características, ya que la geometría de su región restringida permite que los valores de los coeficientes sean inertes hasta cero.
- Un valor alfa de cero en cualquiera de los modelos ridge o lasso tendrá resultados similares al modelo de regresión.
- Cuanto mayor sea el valor alfa, más agresiva será la penalización.
Puedes encontrar un cuaderno más robusto y completo para la implementación en python aquí, o hacer una inmersión profunda en las regresiones con nuestro curso Introducción a la regresión en Python.
