Las técnicas de clasificación son una parte esencial de las aplicaciones de machine learning y minería de datos. Aproximadamente el 70 % de los problemas en ciencia de datos son problemas de clasificación. Existen muchos problemas de clasificación, pero la regresión logística es habitual y es un método de regresión útil para resolver el problema de clasificación binaria. Otra categoría de clasificación es la clasificación multinomial, que trata los problemas en los que hay varias clases presentes en la variable objetivo. Por ejemplo, el conjunto de datos IRIS es un ejemplo muy famoso de clasificación multiclase. Otros ejemplos son la clasificación de categorías de artículos/blogs/documentos.
La regresión logística puede utilizarse para diversos problemas de clasificación, como la detección de spam. Predicción de la diabetes, si un determinado cliente comprará un producto concreto o se irá a otro competidor, si el usuario hará clic o no en un determinado enlace publicitario, y muchos ejemplos más hay en el cubo.
La regresión logística es uno de los algoritmos de machine learning más sencillos y utilizados para la clasificación de dos clases. Es fácil de aplicar y puede utilizarse como base para cualquier problema de clasificación binaria. Sus conceptos básicos fundamentales también son constructivos en el aprendizaje profundo. La regresión logística describe y estima la relación entre una variable binaria dependiente y variables independientes.
Practica la regresión logística en Python con este ejercicio práctico.
¿Qué es la regresión logística?
La regresión logística es un método estadístico para predecir clases binarias. La variable de resultado u objetivo es de naturaleza dicotómica. Dicotómico significa que solo hay dos clases posibles. Por ejemplo, puede utilizarse para problemas de detección del cáncer. Calcula la probabilidad de que se produzca un suceso.
Es un caso especial de regresión lineal en el que la variable objetivo es de naturaleza categórica. Utiliza un logaritmo de probabilidades como variable dependiente. La regresión logística predice la probabilidad de ocurrencia de un suceso binario utilizando una función logit.
Ecuación de regresión lineal:

Donde “y” es una variable dependiente y x1, x2 ... y Xn son variables explicativas.
Función sigmoidea:
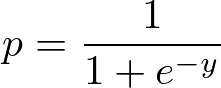
Aplica la función sigmoidea a la regresión lineal:
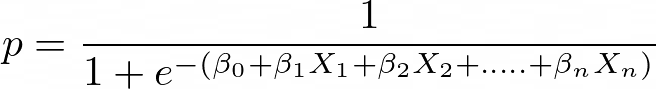
Propiedades de la regresión logística:
- La variable dependiente en la regresión logística sigue la distribución de Bernoulli.
- La estimación se realiza mediante máxima verosimilitud.
- Sin R Square, la adecuación del modelo se calcula mediante concordancia y estadística KS.
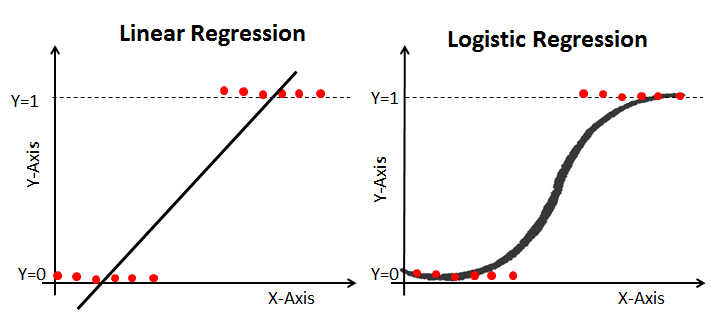
Regresión lineal vs. regresión logística
La regresión lineal te da un resultado continuo, pero la regresión logística te da un resultado constante. Un ejemplo de producción continua es el precio de la vivienda y el precio de las acciones. Ejemplos de resultados discretos son predecir si un paciente tiene cáncer o no, predecir si el cliente cambiará de opinión. La regresión lineal se estima mediante mínimos cuadrados ordinarios (MCO), mientras que la regresión logística se estima mediante el método de estimación de máxima verosimilitud (EML).
Estimación de máxima verosimilitud vs. método de los mínimos cuadrados
El MLE es un método de maximización de la "verosimilitud", mientras que el MCO es un método de aproximación que minimiza la distancia. La maximización de la función de verosimilitud determina los parámetros que tienen más probabilidades de producir los datos observados. Desde un punto de vista estadístico, el MLE establece la media y la varianza como parámetros para determinar los valores paramétricos específicos de un modelo dado. Este conjunto de parámetros puede utilizarse para predecir los datos necesarios en una distribución normal.
Las estimaciones por mínimos cuadrados ordinarios se calculan ajustando a los puntos de datos dados una recta de regresión que tenga la suma mínima de las desviaciones al cuadrado (error cuadrático mínimo). Ambos se utilizan para estimar los parámetros de un modelo de regresión lineal. La MLE asume una función de masa de probabilidad conjunta, mientras que la MCO no requiere ningún supuesto estocástico para minimizar la distancia.
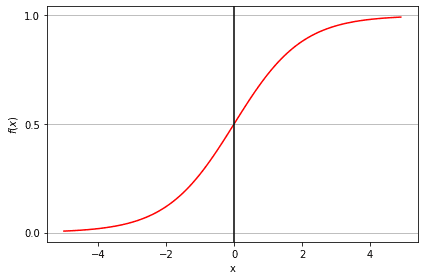
Función sigmoidea
La función sigmoidea, también llamada función logística, da una curva en forma de "S" que puede tomar cualquier número de valor real y convertirlo en un valor entre 0 y 1. Si la curva va al infinito positivo, y predicha se convertirá en 1, y si la curva va al infinito negativo, y predicha se convertirá en 0. Si la salida de la función sigmoidea es superior a 0,5, podemos clasificar el resultado como 1 o SÍ, y si es inferior a 0,5, podemos clasificarlo como 0 o NO. Por ejemplo: Si el resultado es 0,75, podemos decir en términos de probabilidad: Hay un 75 % de probabilidades de que un paciente sufra cáncer.

Tipos de regresión logística
Tipos de regresión logística:
- Regresión logística binaria: La variable objetivo solo tiene dos resultados posibles, como spam o no spam, cáncer o no cáncer.
- Regresión logística multinomial: La variable objetivo tiene tres o más categorías nominales, como predecir el tipo de vino.
- Regresión logística ordinal: la variable objetivo tiene tres o más categorías ordinales, como la valoración de un restaurante o un producto de 1 a 5.
Ejecuta y edita el código de este tutorial en línea
Ejecutar códigoConstrucción de modelos en Scikit-learn
Construyamos el modelo de predicción de la diabetes.
Aquí vas a predecir la diabetes con el clasificador de regresión logística.
En primer lugar, carguemos el conjunto de datos necesario sobre la diabetes de los indios Pima utilizando la función de lectura CSV de pandas. Puedes descargar los datos desde el siguiente enlace: https://www.kaggle.com/uciml/pima-indians-diabetes-database o seleccionar un conjunto de datos de DataCamp: https://www.datacamp.com/workspace/datasets. El conjunto de datos listo para usar te ofrece la opción de entrenar el modelo en el espacio de trabajo de DataCamp, DataCamp Workspace, que es un cuaderno Jupyter gratuito en la nube.
Cargar los datos
Simplificaremos las columnas proporcionando col_names a la función pandas read_csv().
#import pandas
import pandas as pd
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
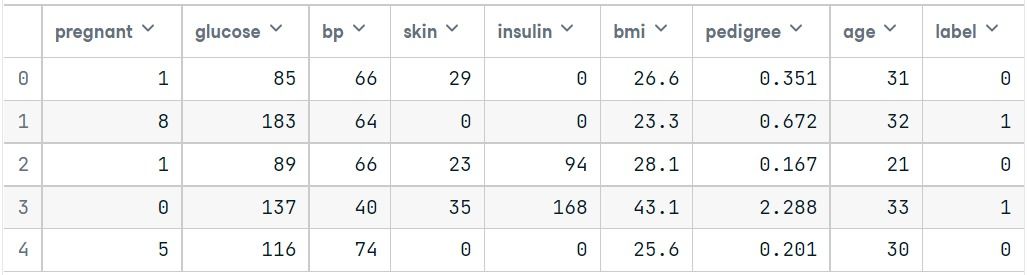
pima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()Seleccionar característica
Aquí, tienes que dividir las columnas dadas en dos tipos de variables: dependiente (o variable objetivo) e independiente (o variables características).
#split dataset in features and target variable
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableDividir los datos
Para comprender el rendimiento del modelo, dividir el conjunto de datos en un conjunto de entrenamiento y un conjunto de prueba es una buena estrategia.
Vamos a dividir el conjunto de datos mediante la función train_test_split(). Tienes que pasar 3 parámetros: características, objetivo y tamaño del conjunto_prueba. Además, puedes utilizar random_state para seleccionar registros aleatoriamente.
# split X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=16)Aquí, el conjunto de datos se divide en dos partes en una proporción de 75:25. Significa que el 75 % de los datos se utilizarán para el entrenamiento del modelo y el 25 % para la prueba del modelo.
Desarrollo y predicción de modelos
En primer lugar, importa el módulo Regresión logística y crea un objeto clasificador de Regresión logística utilizando la función LogisticRegression() con random_state para la reproducibilidad.
A continuación, ajusta tu modelo al conjunto de entrenamiento mediante fit() y realiza la predicción en el conjunto de prueba mediante predict().
# import the class
from sklearn.linear_model import LogisticRegression
# instantiate the model (using the default parameters)
logreg = LogisticRegression(random_state=16)
# fit the model with data
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)Evaluación del modelo mediante la matriz de confusión
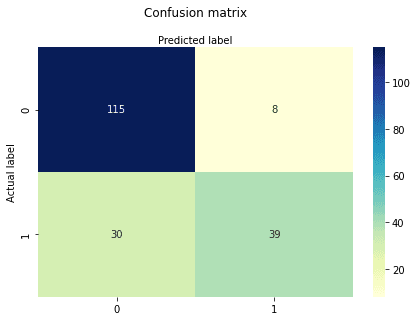
Una matriz de confusión es una tabla que se utiliza para evaluar el rendimiento de un modelo de clasificación. También puedes visualizar el rendimiento de un algoritmo. Lo fundamental de una matriz de confusión es el número de predicciones correctas e incorrectas sumadas por clases.
# import the metrics class
from sklearn import metrics
cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
cnf_matrixarray([[115, 8],
[ 30, 39]])Aquí puedes ver la matriz de confusión en forma de objeto matriz. La dimensión de esta matriz es 2*2 porque este modelo es de clasificación binaria. Tienes dos clases 0 y 1. Los valores diagonales representan predicciones exactas, mientras que los elementos no diagonales son predicciones inexactas. En la salida, 115 y 39 son predicciones reales, y 30 y 8 son predicciones incorrectas.
Visualización de la matriz de confusión mediante un mapa de calor
Vamos a visualizar los resultados del modelo en forma de matriz de confusión utilizando matplotlib y seaborn.
Aquí, visualizarás la matriz de confusión utilizando Heatmap.
# import required modules
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
class_names=[0,1] # name of classes
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)
# create heatmap
sns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
Text(0.5,257.44,'Predicted label');Métricas de evaluación de la matriz de confusión
Vamos a evaluar el modelo utilizando classification_report para ver la exactitud, la precisión y la recuperación.
from sklearn.metrics import classification_report
target_names = ['without diabetes', 'with diabetes']
print(classification_report(y_test, y_pred, target_names=target_names)) precision recall f1-score support
without diabetes 0.79 0.93 0.86 123
with diabetes 0.83 0.57 0.67 69
accuracy 0.80 192
macro avg 0.81 0.75 0.77 192
weighted avg 0.81 0.80 0.79 192Ha obtenido un índice de clasificación del 80 %, lo que se considera una buena precisión.
Precisión: La precisión consiste en ser preciso, es decir, lo exacto que es tu modelo. En otras palabras, puedes decir, cuando un modelo hace una predicción, con qué frecuencia acierta. En tu caso de predicción, cuando tu modelo de Regresión Logística predijo que los pacientes iban a padecer diabetes, ese 73 % de las veces.
Recuérdalo: Si hay pacientes que tienen diabetes en el conjunto de pruebas y tu modelo de regresión logística puede identificarla el 57 % de las veces.
Curva ROC
La curva ROC (característica operativa del receptor) es un gráfico de la tasa de verdaderos positivos frente a la tasa de falsos positivos. Muestra el compromiso entre sensibilidad y especificidad.
y_pred_proba = logreg.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()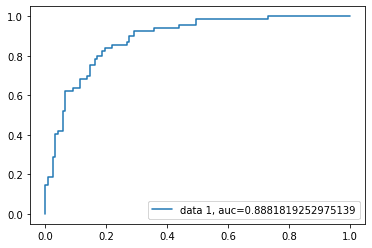
La puntuación AUC del caso es de 0,88. La puntuación AUC 1 representa un clasificador perfecto, y 0,5 representa un clasificador inútil.
El código fuente está disponible en DataCamp Workspace: Comprender la regresión logística en Python.
Ventajas
Debido a su naturaleza eficiente y directa, no requiere una gran potencia de cálculo, es fácil de aplicar, fácilmente interpretable y muy utilizado por analistas de datos y científicos. Además, no requiere escalado de funciones. La regresión logística proporciona una puntuación de probabilidad para las observaciones.
Desventajas
La regresión logística no es capaz de manejar un gran número de características/variables categóricas. Es vulnerable al sobreajuste. Además, no se puede resolver el problema no lineal con la regresión logística, por eso requiere una transformación de características no lineales. La regresión logística no funcionará bien con variables independientes que no estén correlacionadas con la variable objetivo y sean muy similares o estén correlacionadas entre sí.
Conclusión
En este tutorial, has cubierto muchos detalles sobre la regresión logística. Has aprendido qué es la regresión logística, cómo construir los modelos respectivos, cómo visualizar los resultados y algunos antecedentes teóricos. Además, has tratado algunos conceptos básicos como la función sigmoidea, la máxima verosimilitud, la matriz de confusión y la curva ROC.
Esperamos que ahora puedas utilizar la técnica de regresión logística para analizar tus propios conjuntos de datos. ¡Gracias por leer este tutorial!
Si quieres saber más sobre la regresión logística, sigue el curso Machine learning con scikit-learn de DataCamp. También puedes iniciar tu camino para convertirte en ingeniero de machine learning inscribiéndote en el programa de carrera científico de machine learning con Python.