Cadenas de Markov en Python: Tutorial para principiantes

Una cadena de Markov es un sistema matemático que suele definirse como una colección de variables aleatorias que pasan de un estado a otro según ciertas reglas probabilísticas. Estos conjuntos de transición satisfacen la Propiedad de Markov, que establece que la probabilidad de transición a cualquier estado concreto depende únicamente del estado actual y del tiempo transcurrido, y no de la secuencia de estados que lo precedieron. Esta característica única de los procesos de Markov hace que no tengan memoria.

¿Quieres abordar más temas de estadística con Python? ¡Echa un vistazo al curso de Pensamiento Estadístico en Python de DataCamp!

Hagamos la transición...

¿Por qué cadenas de Markov?

Las Cadenas de Markov tienen un uso prolífico en matemáticas. Se emplean ampliamente en economía, teoría de juegos, teoría de la comunicación, genética y finanzas. Surgen ampliamente en contextos estadísticos, especialmente en la estadística bayesiana y en la teoría de la información. Cuando se trata de problemas del mundo real, se utilizan para postular soluciones para estudiar sistemas de control de crucero en vehículos de motor, colas o filas de clientes que llegan a un aeropuerto, tipos de cambio de divisas, etc. El algoritmo conocido como PageRank, que se propuso originalmente para el buscador de Internet Google, se basa en un proceso de Markov. El Simulador de Subreddit de Reddit es un subreddit totalmente automatizado que genera envíos y comentarios aleatorios mediante cadenas de markov, ¡genial!

Cadena de Markov

Una cadena de Markov es un proceso aleatorio con la propiedad de Markov. Un proceso aleatorio o a menudo llamado propiedad estocástica es un objeto matemático definido como una colección de variables aleatorias. Una cadena de Markov tiene un espacio de estados discreto (conjunto de valores posibles de las variables aleatorias) o un conjunto de índices discreto (que a menudo representa el tiempo) - dado el hecho, existen muchas variaciones para una cadena de Markov. Normalmente, el término "cadena de Markov" se reserva para un proceso con un conjunto discreto de tiempos, es decir, una cadena de Markov de Tiempo Discreto (CMDT).

Cadena de Markov en tiempo discreto

Una cadena de Markov de tiempo discreto implica un sistema que se encuentra en un estado determinado en cada paso, con el estado cambiando aleatoriamente entre pasos. A menudo se piensa en los pasos como momentos en el tiempo (pero también podrías referirte a la distancia física o a cualquier otra medida discreta). Una cadena de Markov de tiempo discreto es una secuencia de variables aleatorias _X1, _X2, _X3, ... con la propiedad de Markov, tal que la probabilidad de pasar al siguiente estado depende sólo del estado actual y no de los estados anteriores. Poner esto es una fórmula matemática probabilística:

Pr( _Xn+1 = x | _X1 = _x1, _X2 = _x2, ..., _Xn = _xn) = Pr( _Xn+1 = x | _Xn = _xn)

Como puedes ver, la probabilidad de _Xn+1 sólo depende de la probabilidad de _Xn que la precede. Lo que significa que el conocimiento del estado anterior es todo lo necesario para determinar la distribución de probabilidad del estado actual, satisfaciendo la regla de la independencia condicional (o dicho de otra forma: sólo necesitas conocer el estado actual para determinar el estado siguiente).

Los posibles valores de _Xi forman un conjunto contable S llamado espacio de estados de la cadena. El espacio de estados puede ser cualquier cosa: letras, números, resultados de baloncesto o condiciones meteorológicas. Aunque el parámetro temporal suele ser discreto, el espacio de estados de una cadena de Markov de tiempo discreto no tiene restricciones ampliamente consensuadas, y más bien se refiere a un proceso en un espacio de estados arbitrario. Sin embargo, muchas aplicaciones de las cadenas de Markov emplean espacios de estados finitos o contablemente infinitos, porque tienen un análisis estadístico más sencillo.

Modelo

Una cadena de Markov se representa mediante un autómata probabilístico (¡Sólo suena complicado!). Los cambios de estado del sistema se denominan transiciones. Las probabilidades asociadas a los distintos cambios de estado se denominan probabilidades de transición. Un autómata probabilístico incluye la probabilidad de una transición determinada en la función de transición, convirtiéndola en una matriz de transición.

Puedes pensar en ello como una secuencia de grafos dirigidos, donde las aristas del grafo n están etiquetadas por las probabilidades de pasar de un estado en el momento n a los otros estados en el momento n+1, Pr(_Xn+1 = x | _Xn = _xn). Puedes leer esto como, probabilidad de pasar al estado _Xn+1 dado el valor del estado _Xn. La misma información está representada por la matriz de transición del tiempo n al tiempo n+1. Cada estado del espacio de estados se incluye una vez como fila y otra como columna, y cada celda de la matriz te indica la probabilidad de pasar del estado de su fila al de su columna.

Si la cadena de Markov tiene N estados posibles, la matriz será una matriz N x N, tal que la entrada (I, J) sea la probabilidad de transición del estado I al estado J. Además, la matriz de transición debe ser una matriz estocástica, una matriz cuyas entradas en cada fila deben sumar exactamente 1. ¿Por qué? Puesto que cada fila representa su propia distribución de probabilidad.

Así, el modelo se caracteriza por un espacio de estados, una matriz de transición que describe las probabilidades de determinadas transiciones y un estado inicial en el espacio de estados, dado en la distribución inicial.

Un montón de palabras, ¿eh?

Veamos un ejemplo sencillo para entender los conceptos:

Cuando Cj está triste, lo que no es muy habitual: o sale a correr, o se zampa un helado o se echa una siesta.

Por los datos históricos, si pasó durmiendo un día triste. Al día siguiente hay un 60% de probabilidades de que salga a correr, un 20% de que se quede en la cama y un 20% de que se coma un helado.

Cuando está triste y sale a correr, hay un 60% de probabilidades de que salga a correr al día siguiente, un 30% de que se atiborre de helado y sólo un 10% de probabilidades de que pase durmiendo al día siguiente.

Por último, cuando se da un capricho con un helado en un día triste, sólo hay un 10% de probabilidades de que siga comiendo helado al día siguiente también, un 70% de probabilidades de que salga a correr y un 20% de probabilidades de que pase durmiendo al día siguiente.

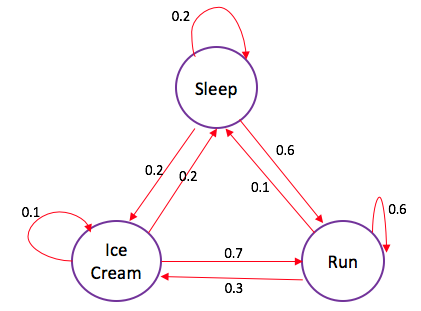
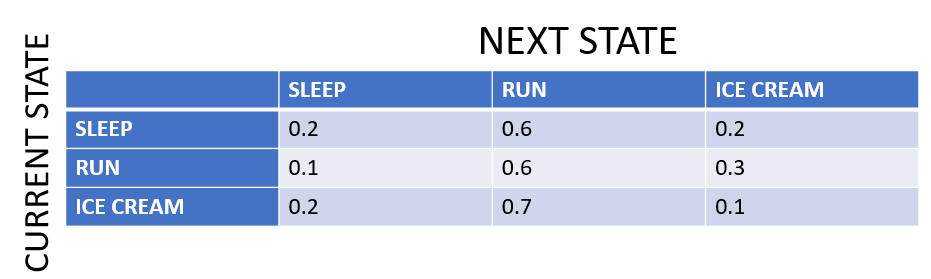
La cadena de Markov representada en el diagrama de estados tiene 3 estados posibles: dormir, correr, helado. Por tanto, la matriz de transición será una matriz de 3 x 3. Observa que las flechas que salen de un estado siempre suman exactamente 1, del mismo modo que las entradas de cada fila de la matriz de transición deben sumar exactamente 1, lo que representa la distribución de probabilidad. En la matriz de transición, las celdas hacen la misma función que las flechas en el diagrama de estados.

Ahora que has visto el ejemplo, esto debería darte una idea de los distintos conceptos relacionados con una cadena de Markov. Pero, ¿cómo y dónde puedes utilizar esta teoría en la vida real?

Con el ejemplo que has visto, ahora puedes responder a preguntas como: "Partiendo del estado: dormir, ¿cuál es la probabilidad de que Cj esté funcionando (estado: funcionar) al final de una triste duración de 2 días?"

Vamos a resolver esto: Para pasar del estado: dormir al estado: correr, Cj debe permanecer en el estado: dormir el primer movimiento (o día), y luego pasar al estado: correr el siguiente (segundo) movimiento (0,2 $\cdot$ 0,6); o pasar al estado: correr el primer día y luego permanecer allí el segundo (0,6 $\cdot$ 0,6) o podría pasar al estado: helado en el primer movimiento y luego al estado: correr en el segundo (0,2 $\cdot$ 0,7). Así que la probabilidad: ((0,2 $\cdot$ 0,6) + (0,6 $\cdot$ 0,6) + (0,2 $\cdot$ 0,7)) = 0,62. Así pues, ahora podemos decir que hay un 62% de probabilidades de que Cj pase al estado: correr después de dos días de estar triste, si empezó en el estado: dormir.

Esperamos que esto te haya dado una idea de las distintas preguntas que puedes responder utilizando una red de cadenas de Markov.

Además, teniendo esto claro, resulta más fácil comprender algunas propiedades importantes de las cadenas de Markov:

• Reducibilidad: se dice que una cadena de Markov es irreducible si es posible llegar a cualquier estado desde cualquier estado. En otras palabras, una cadena de Markov es irreducible si existe una cadena de pasos entre dos estados cualesquiera que tenga probabilidad positiva.
• Periodicidad: un estado de una cadena de Markov es periódico si la cadena sólo puede volver al estado en múltiplos de algún número entero mayor que 1. Así, empezando en el estado "i", la cadena sólo puede volver a "i" en múltiplos del periodo "k", y k es el mayor de dichos números enteros. El estado "i" es aperiódico si k = 1 y periódico si k > 1.
• Transitoriedad y Recurrencia: Se dice que un estado "i" es transitorio si, dado que empezamos en el estado "i", existe una probabilidad distinta de cero de que nunca volvamos a "i". El estado i es recurrente (o persistente) si no es transitorio. Un estado recurrente se denomina recurrente positivo si se espera que vuelva en un número finito de pasos y recurrente nulo en caso contrario.
• Ergodicidad: se dice que un estado "i" es ergódico si es aperiódico y recurrente positivo. Si todos los estados de una cadena de Markov irreducible son ergódicos, se dice que la cadena es ergódica.
• Estado absorbente: un estado i se llama absorbente si es imposible salir de este estado. Por tanto, el estado "i" es absorbente si_pii = 1 y _pij = 0 para i ≠ j. Si cada estado puede alcanzar un estado absorbente, entonces la cadena de Markov es una cadena de Markov absorbente.

Consejo: si quieres ver también una explicación visual de las cadenas de Markov, no dejes de visitar esta página.

Cadenas de Markov en Python

Intentemos codificar el ejemplo anterior en Python. Y aunque en la vida real, probablemente utilizarías una biblioteca que codifique las Cadenas de Markov de forma mucho más eficiente, el código debería ayudarte a empezar...

Primero vamos a importar algunas de las bibliotecas que vas a utilizar.

import numpy as np
import random as rm

Definamos ahora los estados y su probabilidad: la matriz de transición. Recuerda que la matriz va a ser una matriz de 3 X 3, ya que tienes tres estados. Además, tendrás que definir las trayectorias de transición, también puedes hacerlo utilizando matrices.

# The statespace
states = ["Sleep","Icecream","Run"]

# Possible sequences of events
transitionName = [["SS","SR","SI"],["RS","RR","RI"],["IS","IR","II"]]

# Probabilities matrix (transition matrix)
transitionMatrix = [[0.2,0.6,0.2],[0.1,0.6,0.3],[0.2,0.7,0.1]]

Asegúrate siempre de que las probabilidades suman 1. Y no está de más dejar mensajes de error, ¡al menos cuando se codifica!

if sum(transitionMatrix[0])+sum(transitionMatrix[1])+sum(transitionMatrix[1]) != 3:
    print("Somewhere, something went wrong. Transition matrix, perhaps?")
else: print("All is gonna be okay, you should move on!! ;)")

All is gonna be okay, you should move on!! ;)

Ahora vamos a codificar la cosa real. Utilizarás la página numpy.random.choice para generar una muestra aleatoria del conjunto de transiciones posibles. Aunque la mayoría de sus argumentos se explican por sí mismos, p puede que no. Es un argumento opcional que te permite introducir la distribución de probabilidad para el conjunto de muestreo, que en este caso es la matriz de transición.

# A function that implements the Markov model to forecast the state/mood.
def activity_forecast(days):
    # Choose the starting state
    activityToday = "Sleep"
    print("Start state: " + activityToday)
    # Shall store the sequence of states taken. So, this only has the starting state for now.
    activityList = [activityToday]
    i = 0
    # To calculate the probability of the activityList
    prob = 1
    while i != days:
        if activityToday == "Sleep":
            change = np.random.choice(transitionName[0],replace=True,p=transitionMatrix[0])
            if change == "SS":
                prob = prob * 0.2
                activityList.append("Sleep")
                pass
            elif change == "SR":
                prob = prob * 0.6
                activityToday = "Run"
                activityList.append("Run")
            else:
                prob = prob * 0.2
                activityToday = "Icecream"
                activityList.append("Icecream")
        elif activityToday == "Run":
            change = np.random.choice(transitionName[1],replace=True,p=transitionMatrix[1])
            if change == "RR":
                prob = prob * 0.5
                activityList.append("Run")
                pass
            elif change == "RS":
                prob = prob * 0.2
                activityToday = "Sleep"
                activityList.append("Sleep")
            else:
                prob = prob * 0.3
                activityToday = "Icecream"
                activityList.append("Icecream")
        elif activityToday == "Icecream":
            change = np.random.choice(transitionName[2],replace=True,p=transitionMatrix[2])
            if change == "II":
                prob = prob * 0.1
                activityList.append("Icecream")
                pass
            elif change == "IS":
                prob = prob * 0.2
                activityToday = "Sleep"
                activityList.append("Sleep")
            else:
                prob = prob * 0.7
                activityToday = "Run"
                activityList.append("Run")
        i += 1  
    print("Possible states: " + str(activityList))
    print("End state after "+ str(days) + " days: " + activityToday)
    print("Probability of the possible sequence of states: " + str(prob))

# Function that forecasts the possible state for the next 2 days
activity_forecast(2)

Start state: Sleep
Possible states: ['Sleep', 'Sleep', 'Run']
End state after 2 days: Run
Probability of the possible sequence of states: 0.12

Obtienes un conjunto aleatorio de transiciones posibles junto con la probabilidad de que ocurra, partiendo del estado: Duerme. Amplía aún más el programa para iterarlo quizá un par de cientos de veces con el mismo estado inicial, entonces podrás ver la probabilidad esperada de acabar en cualquier estado concreto junto con su probabilidad. Reescribamos la función activity_forecast y añadamos un nuevo conjunto de bucles para hacerlo...

def activity_forecast(days):
    # Choose the starting state
    activityToday = "Sleep"
    activityList = [activityToday]
    i = 0
    prob = 1
    while i != days:
        if activityToday == "Sleep":
            change = np.random.choice(transitionName[0],replace=True,p=transitionMatrix[0])
            if change == "SS":
                prob = prob * 0.2
                activityList.append("Sleep")
                pass
            elif change == "SR":
                prob = prob * 0.6
                activityToday = "Run"
                activityList.append("Run")
            else:
                prob = prob * 0.2
                activityToday = "Icecream"
                activityList.append("Icecream")
        elif activityToday == "Run":
            change = np.random.choice(transitionName[1],replace=True,p=transitionMatrix[1])
            if change == "RR":
                prob = prob * 0.5
                activityList.append("Run")
                pass
            elif change == "RS":
                prob = prob * 0.2
                activityToday = "Sleep"
                activityList.append("Sleep")
            else:
                prob = prob * 0.3
                activityToday = "Icecream"
                activityList.append("Icecream")
        elif activityToday == "Icecream":
            change = np.random.choice(transitionName[2],replace=True,p=transitionMatrix[2])
            if change == "II":
                prob = prob * 0.1
                activityList.append("Icecream")
                pass
            elif change == "IS":
                prob = prob * 0.2
                activityToday = "Sleep"
                activityList.append("Sleep")
            else:
                prob = prob * 0.7
                activityToday = "Run"
                activityList.append("Run")
        i += 1    
    return activityList

# To save every activityList
list_activity = []
count = 0

# `Range` starts from the first count up until but excluding the last count
for iterations in range(1,10000):
        list_activity.append(activity_forecast(2))

# Check out all the `activityList` we collected    
#print(list_activity)

# Iterate through the list to get a count of all activities ending in state:'Run'
for smaller_list in list_activity:
    if(smaller_list[2] == "Run"):
        count += 1

# Calculate the probability of starting from state:'Sleep' and ending at state:'Run'
percentage = (count/10000) * 100
print("The probability of starting at state:'Sleep' and ending at state:'Run'= " + str(percentage) + "%")

The probability of starting at state:'Sleep' and ending at state:'Run'= 62.419999999999995%

¿Cómo nos aproximamos al 62% deseado?

Nota En realidad se trata de la "ley de los grandes números", que es un principio de probabilidad que afirma que las frecuencias de los sucesos con la misma probabilidad de ocurrir se igualan, pero sólo si hay suficientes ensayos o instancias. En otras palabras, a medida que aumente el número de experimentos, la proporción real de resultados convergerá en una proporción teórica o esperada de resultados.

Estado mental de Markov

Con esto concluye el tutorial sobre Cadenas de Markov. Te han presentado las Cadenas de Markov y has visto algunas de sus propiedades. Las cadenas de Markov simples son uno de los temas necesarios y fundamentales para iniciarse en la ciencia de datos en Python. Si quieres más recursos para iniciarte en la estadística en Python, no dejes de consultar esta página.

¿Te interesa explorar más casos prácticos con estadísticas en Python? Echa un vistazo a los cursos Estudios de Casos en Pensamiento Estadístico o Análisis de Redes en Python de DataCamp.