Tutorial de ecuación normal para regresión lineal

La mayoría de los problemas con los que nos encontramos tienen varias formas de resolverse. Por ejemplo, si quisiéramos ir de un lado a otro de una habitación, podríamos decidir rodearla hasta llegar al lado opuesto o simplemente atravesarla.

La ecuación normal no es más que un énfasis de este concepto. Es solo otra forma de resolver un problema. ¿Qué problema has planteado? Lo trataremos en el resto de este artículo. Por ahora, todo lo que necesitas saber es que se trata de un enfoque eficaz que puede ayudarte a ahorrar mucho tiempo al aplicar la regresión lineal en determinadas condiciones.

Vamos a profundizar...

¿Qué es la ecuación normal?

La ecuación normal es una solución de forma cerrada que se utiliza para encontrar el valor de θ que minimiza la función de coste. Otra forma de describir la ecuación normal es como un algoritmo de un paso utilizado para encontrar analíticamente los coeficientes que minimizan la función de pérdida. Ambas descripciones funcionan, pero ¿qué significan exactamente? Empezaremos con la regresión lineal.

La regresión lineal hace una predicción, y_hat, y calcula la suma ponderada de las características de entrada más un término de sesgo. Matemáticamente se puede representar de la siguiente manera:

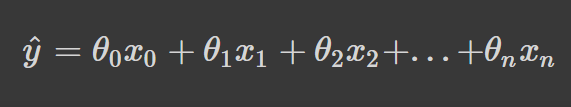
Donde θ representa los parámetros y n es el número de características.

Esencialmente, todo lo que ocurre en la ecuación anterior es el producto punto de θ, y se está sumando x. Por tanto, una forma más concisa de representarlo es utilizar su forma vectorizada:

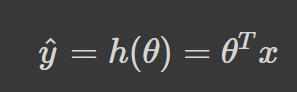
h(θ) es la función de hipótesis.

Dada esta función objetivo aproximada, podemos utilizar nuestro modelo para hacer predicciones. Para determinar si nuestro modelo ha aprendido bien, es importante que midamos su rendimiento en los datos de entrenamiento. Para ello, calculamos una función de pérdida. El objetivo del proceso de entrenamiento es encontrar los valores de theta (θ) que minimicen la función de pérdida.

Así es como podemos representar matemáticamente nuestra función de pérdida:

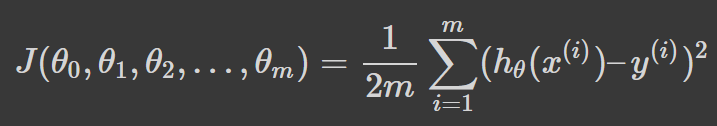
En la ecuación anterior, theta (θ) es un vector de dimensión n + 1, y nuestra función de pérdida es una función del valor del vector. En consecuencia, hay que tomar la derivada parcial de la función de pérdida, J, con respecto a cada parámetro de θ_j sucesivamente. Todos ellos deben ser iguales a cero. Al seguir este proceso y resolver para todos los valores de θ desde θ_0 hasta θ_n se obtendrán los valores de θ que minimizan la función de pérdida.

Trabajar a través de la solución de los parámetros θ_0 a θ_n mediante el proceso descrito anteriormente da como resultado un procedimiento de derivación extremadamente complicado. En efecto, existe una solución más rápida.

Echa un vistazo a la fórmula de la ecuación normal:

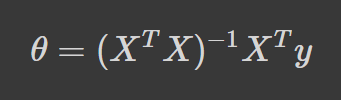
Donde:

θ → Los parámetros que minimizan la función de pérdida X → Los valores de las características de entrada de cada instancia y → El vector de valores de salida de cada instancia

La ecuación normal frente al descenso de gradiente

Aunque ambos métodos tratan de encontrar los parámetros theta (θ) que minimicen la función de pérdida, el método de aproximación difiere mucho entre las dos soluciones.

Como ya hemos tratado el funcionamiento de la ecuación normal en "¿Qué es la ecuación normal?", en este apartado abordaremos brevemente el descenso por gradiente y, a continuación, expondremos en qué se diferencian ambas técnicas.

Descenso de gradiente

El descenso de gradiente es uno de los algoritmos de machine learning más utilizados en machine learning. Se despliega para encontrar iterativamente los parámetros theta (θ) que minimizan la función de pérdida.

El proceso comienza mediante la evaluación primero el rendimiento del modelo. A continuación, se calcula la derivada parcial de la función de pérdida, que se utiliza para referenciar la pendiente en su punto actual. Por último, damos pasos proporcionales al gradiente negativo para realizar un descenso al mínimo de la función de pérdida al actualizar el conjunto actual de parámetros (véase la fórmula a continuación).

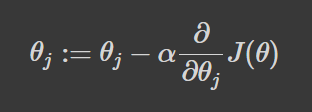
Este proceso se repite hasta la convergencia en el mínimo de la función de pérdida.

¿En qué se diferencian?

La forma más obvia en que la ecuación normal difiere del descenso de gradiente es que es analítica. El descenso de gradiente adopta un enfoque iterativo, lo que significa que nuestros parámetros se actualizan gradualmente hasta la convergencia. Otra sutil diferencia es que el descenso de gradiente requiere que definamos una tasa de aprendizaje que controle el tamaño de los pasos dados hacia el mínimo de la función de pérdida. La ecuación normal no requiere que definamos un ritmo de aprendizaje porque no estamos dando pasos iterativos: obtenemos los resultados directamente.

Además, el escalado de rasgos no es necesario cuando utilizamos el enfoque de la ecuación normal; normalmente realizamos el escalado de rasgos para asegurarnos de que nuestros rasgos tienen un rango similar de valores. Esto se debe a que el descenso de gradiente es sensible a los rangos de nuestros puntos de datos. No normalizar nuestras características cuando utilizamos el descenso de gradiente puede introducir asimetría en el gráfico de contorno de la función de pérdida, pero la ecuación normal no sufre este problema.

Descifrar cuándo utilizar la ecuación normal

La mejor forma de saber si debes utilizar la ecuación normal en lugar del descenso de gradiente es comprender sus desventajas.

Calcular la ecuación normal se convierte en un reto computacional cuando el número de características de nuestro conjunto de datos es grande. El motivo es que, para resolver los parámetros θ, hay que calcular el término (X' X)^-1. El cálculo de X' X produce una matriz n x n y, para la mayoría de las implementaciones informáticas, la conversión de una matriz crece aproximadamente como el cubo de las dimensiones de la matriz. Esto significa que la operación inversa se ejecuta con una complejidad de tiempo O(n^3), lo que hace que la ecuación normal se ejecute con extrema lentitud cuando n es muy grande (más información sobre la complejidad temporal).

Por tanto, es mejor utilizar el descenso de gradiente cuando el número de características del conjunto de datos es grande. Andrew Ng, un destacado experto en machine learning e IA, recomienda que te plantees utilizar el descenso de gradiente cuando el número de características, n, sea superior a 10 000. Para 10 000 características o menos, puede ser mejor que utilices la ecuación normal, ya que no tienes que seleccionar un valor para la tasa de aprendizaje, lo que significa que tienes un hiperparámetro menos que ajustar.

La ecuación normal desde cero en Python

Vamos a generar un problema de regresión para comprobar esta ecuación:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression

# Generate a regression problem
X, y = make_regression(
    n_samples=100,
    n_features=2,
    n_informative=2,
    noise = 10,
    random_state=25
    )

# Visualize feature at index 1 vs target
plt.subplots(figsize=(8, 5))
plt.scatter(X[:, 1], y, marker='o')
plt.xlabel("Feature at Index 1")
plt.ylabel("Target")
plt.show()

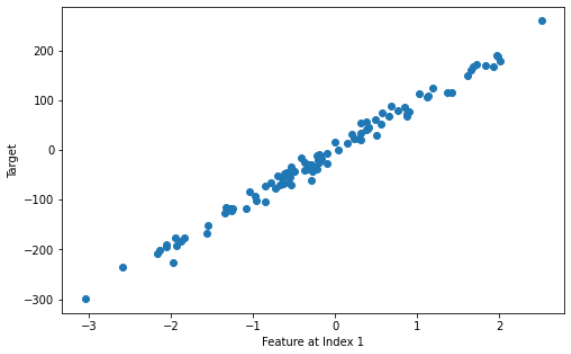
Aquí es donde aplicaremos la ecuación normal:

# adds x0 = 1 to each instance
X_b = np.concatenate([np.ones((len(X), 1)), X], axis=1)
# calculate normal equation
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
# best values for theta
intercept, *coef = theta_best
print(f"Intercept: {intercept}\n\
Coefficients: {coef}")

Intercept: 0.35921242677977794
Coefficients: [6.129199175400593, 96.44309685893134]

Pongamos a prueba nuestro modelo mediante una predicción:

# making a new sample
new_sample = np.array([[-2, 0.25]])
# adding a bias term to the instance
new_sample_b = np.concatenate([np.ones((len(new_sample), 1)), new_sample], axis=1)
# predicting the value of our new sample
new_sample_pred = new_sample_b.dot(theta_best)
print(f"Prediction: {new_sample_pred}")
Prediction: [12.21158829]

Cuando implementas un algoritmo de machine learning desde cero, siempre es útil disponer de un método para validar tu solución; Scikit-learn es una de las bibliotecas de machine learning más populares en Python. Presenta varias implementaciones de distintos algoritmos, incluida la regresión lineal, que utilizaremos para validar nuestra ecuación normal.

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(X, y)

print(f"Intercept: {lr.intercept_}\n\
Coefficients: {lr.coef_}")
print(f"Prediction: {lr.predict(new_sample)}")

Intercept: 0.3592124267797807
Coefficients: [ 6.12919918 96.44309686]
Prediction: [12.21158829]

Las soluciones son aproximadamente iguales, por lo que podemos confirmar que nuestra solución es correcta.