Explicación de las funciones de pérdida en el machine learning

El machine learning proporciona modelos computacionales con capacidad para hacer predicciones, clasificaciones y decisiones basadas en datos. Como campo de estudio, el machine learning es un subconjunto del dominio de la inteligencia artificial, que engloba los procesos implicados en la construcción de un modelo computacional con capacidades que imitan la inteligencia humana y, en algunos casos, la superan.

El machine learning y los algoritmos y técnicas asociados implican fundamentalmente diseñar, implementar y entrenar algoritmos para reconocer patrones en datos expuestos y realizar predicciones o clasificaciones.

Los algoritmos de machine learning aprenden mediante distintos métodos, pero un componente fundamental del proceso de aprendizaje de los algoritmos y modelos de machine learning es la función de pérdida. La función de pérdida es un proceso matemático que cuantifica el margen de error entre la predicción de un modelo y el valor objetivo real. Más adelante en este artículo, exploraremos en detalle la función de pérdida.

Funciones de pérdida en breve

La clave es que la función de pérdida es una forma cuantificable de medir el rendimiento y la precisión de un modelo de machine learning. En este caso, la función de pérdida actúa como guía para el proceso de aprendizaje dentro de un modelo o algoritmo de machine learning.

El papel de la función de pérdida es crucial en el entrenamiento de los modelos de machine learning e incluye lo siguiente:

• Medición del rendimiento: Las funciones de pérdida ofrecen una métrica clara para evaluar el rendimiento de un modelo, cuantificando la diferencia entre las predicciones y los resultados reales.
• Dirección para la mejora: Las funciones de pérdida guían la mejora del modelo dirigiendo al algoritmo para que ajuste los parámetros (pesos) de forma iterativa para reducir la pérdida y mejorar las predicciones.
• Equilibrar el sesgo y la varianza: Las funciones de pérdida eficaces ayudan a equilibrar el sesgo del modelo (simplificación excesiva) y la varianza (ajuste excesivo), algo esencial para la generalización del modelo a nuevos datos.
• Influir en el comportamiento del modelo: Determinadas funciones de pérdida pueden afectar al comportamiento del modelo, como ser más robusto frente a los datos atípicos o dar prioridad a tipos concretos de errores.

Exploremos el papel de determinadas funciones de pérdida en secciones posteriores y construyamos una intuición y comprensión detalladas de la función de pérdida.

¿Qué es una función de pérdida?

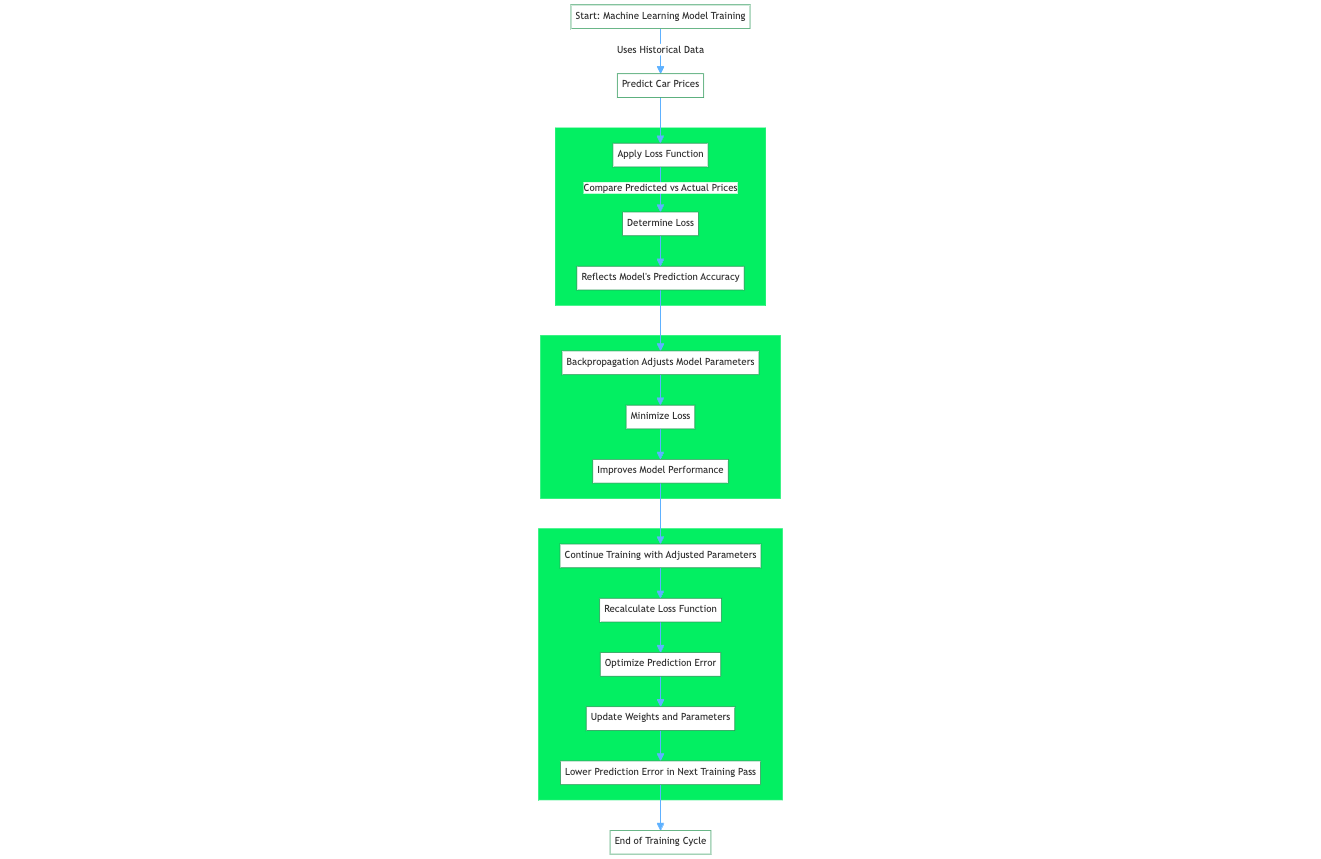
La función de pérdida, también denominada función de error, es un componente crucial en el machine learning que cuantifica la diferencia entre los resultados previstos de un algoritmo de machine learning y los valores objetivo reales. Por ejemplo, en un problema de regresión para predecir el precio de los coches a partir de datos históricos, una función de pérdida evalúa la predicción de una red neuronal a partir de una muestra de entrenamiento del conjunto de datos de entrenamiento. La función de pérdida cuantifica la diferencia o el margen de error entre el precio del coche predicho por la red y el precio real.

El valor resultante, la pérdida, refleja la precisión de las predicciones del modelo. Durante el entrenamiento, un algoritmo de aprendizaje como el algoritmo de retropropagación utiliza el gradiente de la función de pérdida con respecto a los parámetros del modelo para ajustar estos parámetros y minimizar la pérdida, mejorando eficazmente el rendimiento del modelo en el conjunto de datos.

A menudo, los términos función de pérdida y función de coste se utilizan indistintamente; a pesar de ello, ambos términos tienen definiciones distintas:

Como ya se ha dicho, la función de pérdida, también conocida como función de error, cuantifica lo bien que se compara una única predicción del algoritmo de machine learning con el valor objetivo real. La idea clave es que una función de pérdida se aplica a un único ejemplo de entrenamiento y forma parte del proceso global de aprendizaje del modelo, que proporciona la señal mediante la cual el algoritmo de aprendizaje del modelo actualiza los pesos y los parámetros.

La función de coste, a veces llamada función objetivo, es una media de la función de pérdida de todo un conjunto de entrenamiento que contiene varios ejemplos de entrenamiento. La función de coste cuantifica el rendimiento del modelo en todo el conjunto de datos de entrenamiento.

Profundicemos en cómo funcionan las funciones de pérdida.

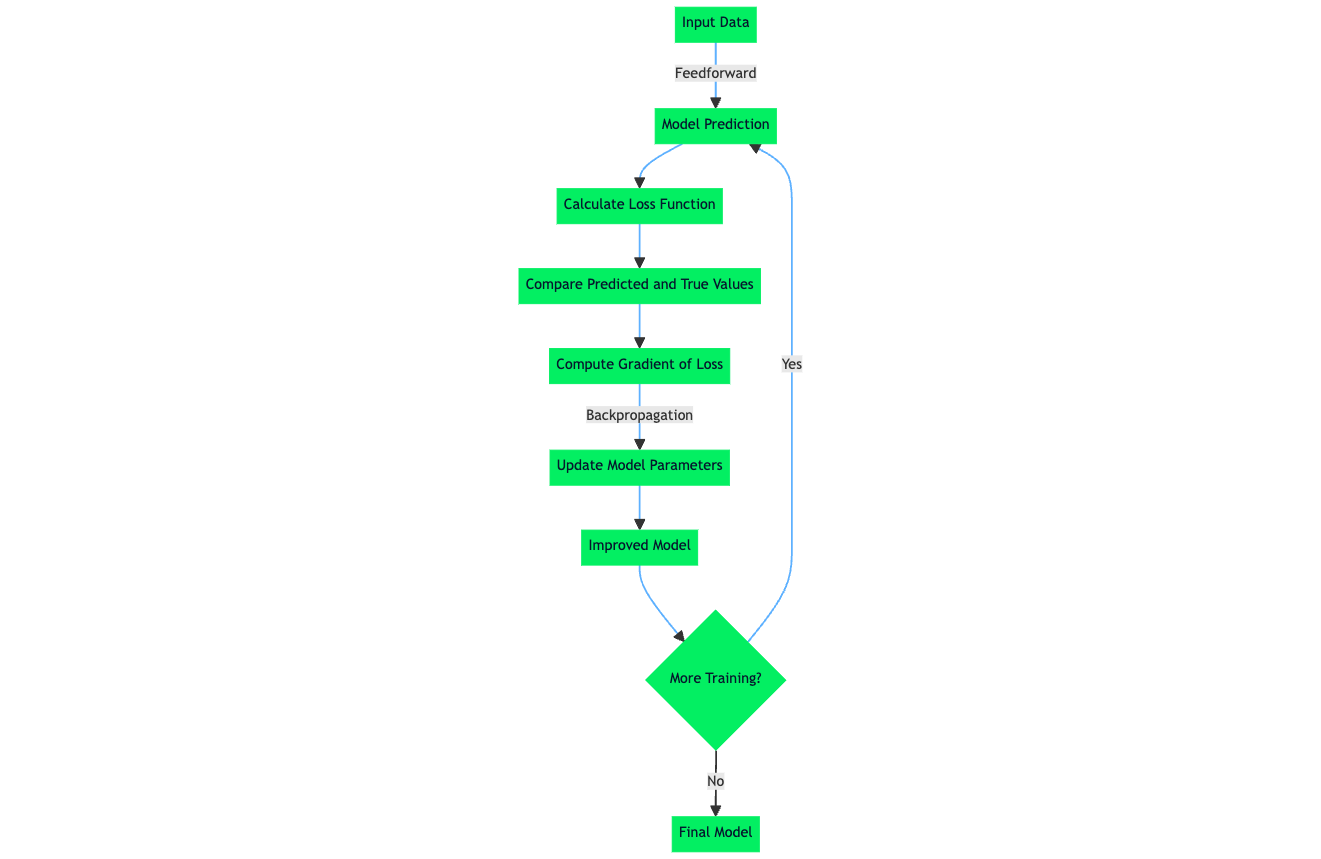
Cómo funcionan las funciones de pérdida

Aunque hay distintos tipos de funciones de pérdida, fundamentalmente, todas operan cuantificando la diferencia entre las predicciones de un modo y el valor objetivo real del conjunto de datos. El término oficial para esta cuantificación numérica es el error de predicción. El algoritmo y los mecanismos de aprendizaje de un modelo de machine learning se optimizan para minimizar el error de predicción, lo que significa que, tras calcular el valor de la función de pérdida, que viene determinado por el error de predicción, el algoritmo de aprendizaje aprovecha esta información para realizar actualizaciones de pesos y parámetros que, en efecto, durante la siguiente pasada de entrenamiento conducen a un error de predicción menor.

Al explorar el tema de la función de pérdida, los algoritmos de machine learning y el proceso de aprendizaje dentro de las redes neuronales, surge el tema de la Minimización Empírica del Riesgo (MRE). La ERM es un enfoque para seleccionar los parámetros óptimos de un algoritmo de machine learning que minimice el riesgo empírico. El riesgo empírico, en este caso, es el conjunto de datos de entrenamiento.

El componente de minimización del riesgo de la ERM es el proceso mediante el cual el algoritmo de aprendizaje interno minimiza el error de predicción del algoritmo de machine learning sobre un conjunto de datos conocido, de forma que el modelo tenga un rendimiento y una precisión esperados en un escenario en el que un conjunto de datos no visto o una muestra de datos que podría tener una distribución estática de datos similar a la del conjunto de datos sobre el que se ha entrenado inicialmente el modelo.

Tipos de funciones de pérdida

Las funciones de pérdida en machine learning se pueden clasificar en función de las tareas de machine learning a las que son aplicables. La mayoría de las funciones de pérdida se aplican a los problemas de regresión y clasificación del machine learning. Se espera que el modelo prediga valores de salida continuos para tareas de machine learning de regresión. En cambio, se espera que el modelo proporcione etiquetas discretas correspondientes a una clase del conjunto de datos para las tareas de clasificación.

A continuación se presentan funciones de pérdida estándar y su clasificación en problemas de machine learning a los que se prestan bien. La mayoría de estas funciones de pérdida se tratan en detalle más adelante en este artículo.

Funciones de pérdida para la regresión

Error cuadrático medio (ECM) / Pérdida L2

El error cuadrático medio (MSE) o pérdida L2 es una función de pérdida que cuantifica la magnitud del error entre la predicción de un algoritmo de machine learning y un resultado real, tomando la media de la diferencia al cuadrado entre las predicciones y los valores objetivo. Al elevar al cuadrado la diferencia entre las predicciones y los valores objetivo reales, se asigna una penalización mayor a las desviaciones más significativas del valor objetivo. Una media de los errores normaliza los errores totales frente al número de muestras de un conjunto de datos u observación.

La ecuación matemática del Error Cuadrático Medio (ECM) o Pérdida L2 es:

MSE = (1/n) * Σ(yᵢ - ȳ)²

Donde:

• n es el número de muestras del conjunto de datos
• yᵢ es el valor previsto para la muestra i-ésima
• ȳ es el valor objetivo de la muestra i-ésima

Cuándo utilizar el MSE

Saber cuándo utilizar el MSE es crucial en el desarrollo de modelos de machine learning. El MSE es una función de pérdida estándar utilizada en la mayoría de las tareas de regresión, ya que dirige el modelo a optimizar para minimizar las diferencias al cuadrado entre los valores predichos y los valores objetivo.

El MSE se recomienda para escenarios de ML en los que favorece el proceso de aprendizaje penalizar significativamente la presencia de valores atípicos. Sin embargo, estas características del MSE no siempre son adecuadas para escenarios y casos de uso en los que los valores atípicos se deben al ruido de los datos, en contraposición a las señales positivas.

Un ejemplo de escenario en el que se aprovecha la función de pérdida MSE es la predicción de precios inmobiliarios o, más ampliamente, la modelización predictiva. Predecir el precio de la vivienda implica utilizar características como el número de habitaciones, la ubicación, la zona, la distancia a los servicios y otras características numéricas. Los precios de la vivienda en una zona localizada se distribuyen normalmente, por lo que el objetivo de penalizar los valores atípicos es esencial para que el modelo pueda predecir con exactitud los precios de la vivienda.

Un pequeño porcentaje de error en el sector inmobiliario puede equivaler a una importante cantidad de dinero. Por ejemplo, un error del 5% en una casa de 200.000 $ son 10.000 $, lo que es sustancial. Por tanto, elevar los errores al cuadrado (como se hace en el MSE) ayuda a dar mayor peso a los errores más grandes, empujando así al modelo a ser más preciso con propiedades de mayor valor.

Error medio absoluto (MAE) / Pérdida L1

El Error medio absoluto (MAE), también conocido como Pérdida L1, es una función de pérdida utilizada en tareas de regresión que calcula las diferencias absolutas medias entre los valores predichos de un modelo de machine learning y los valores reales del objetivo. A diferencia del Error cuadrático medio (ECM), el MAE no eleva al cuadrado las diferencias, tratando todos los errores con el mismo peso, independientemente de su magnitud.

La ecuación matemática del Error Medio Absoluto (MAE) o Pérdida L1 es:

MAE = (1/n) * Σ|yᵢ - ȳ|

Donde:

• n es el número de muestras del conjunto de datos
• yᵢ es el valor previsto para la muestra i-ésima
• ȳ es el valor objetivo de la muestra i-ésima

Cuándo utilizar el MAE

El MAE mide la diferencia absoluta media entre los valores previstos y los reales. A diferencia del MSE, el MAE no eleva al cuadrado las diferencias, lo que lo hace menos sensible a los valores atípicos. Comparado con el Error cuadrático medio (ECM), el Error medio absoluto (EAM) es intrínsecamente menos sensible a los valores atípicos, porque asigna el mismo peso a todos los errores, independientemente de su magnitud.

Esto significa que, aunque un valor atípico puede sesgar significativamente el MSE al contribuir con un error desproporcionadamente grande cuando se eleva al cuadrado, su impacto en el MAE es mucho más contenido. La influencia de un valor atípico en la métrica de error global es mínima cuando se utiliza MAE como función de pérdida. En cambio, el MSE amplifica el efecto de los valores atípicos debido a la elevación al cuadrado de los términos de error, afectando más sustancialmente a la estimación del error del modelo.

Un escenario en el que MAE es una función de pérdida aplicable es aquel en el que no queremos penalizar considerablemente o en absoluto a los valores atípicos, por ejemplo, la predicción de los plazos de entrega de una empresa de reparto de comida.

Una empresa de servicios de reparto, como UberEats, Deliveroo o DoorDash, podría crear un modelo de estimación del reparto para aumentar la satisfacción del cliente. El tiempo que tarda un servicio de reparto en entregar la comida se ve afectado por varios factores, como el tiempo, los incidentes de tráfico, las obras en la carretera, etc.

Manejar estos factores es crucial para estimar los plazos de entrega. Un método para manejar esto es clasificar estos sucesos como atípicos, pero tomar la decisión para asegurarse de que no afecta al modelo que se está entrenando. MAE es una función de pérdida adecuada en este escenario, ya que tratará los puntos de datos atípicos debidos a obras en la carretera o sucesos raros con menor gravedad, reduciendo el efecto de los atípicos en la métrica de error y en el proceso de aprendizaje del modelo.

El MAE, en particular, añade una ponderación de error uniforme a todos los puntos de datos; en el escenario descrito, penalizar los puntos de datos atípicos podría dar lugar a una sobreestimación o subestimación de los plazos de entrega.

Pérdida de Huber / Error medio absoluto suave

La Pérdida Huber o Error medio absoluto suave es una función de pérdida que toma las características ventajosas de las funciones de pérdida Error medio absoluto y Error cuadrático medio y las combina en una única función de pérdida. La naturaleza híbrida de la Pérdida de Huber la hace menos sensible a los valores atípicos, como el MAE, pero también penaliza los errores menores dentro de la muestra de datos, de forma similar al MSE. La función de pérdida de Huber también se utiliza en tareas de machine learning de regresión.

La ecuación matemática de la Pérdida de Huber es la siguiente:

L(δ, y, f(x)) = (1/2) * (f(x) - y)^2   if |f(x) - y| <= δ
               = δ * |f(x) - y| - (1/2) * δ^2   if |f(x) - y| > δ

Donde:

• L representa la función de pérdida de Huber
• δ es el parámetro delta, que determina el umbral para cambiar entre los componentes cuadrático y lineal de la función de pérdida
• y es el valor verdadero o valor objetivo
• f(x) es el valor previsto

Cuándo utilizar la Pérdida de Huber / Error medio absoluto suave

La función de Pérdida de Huber combina eficazmente dos componentes para tratar los errores de forma diferente, con el punto de transición entre estos componentes determinado por el umbral δ:

• Componente cuadrático para errores pequeños: Para errores inferiores a δ, utiliza el componente cuadrático (1/2) * (f(x) - y)^2
• Componente lineal para grandes errores: Para errores mayores que δ, aplica la componente lineal δ * |f(x) - y| - (1/2) * δ^2

La pérdida de Huber funciona en dos modos que se conmutan en función del tamaño de la diferencia calculada entre el valor objetivo real y la predicción del algoritmo de machine learning. El término clave dentro de la Pérdida de Huber es delta (δ). Delta es un umbral que determina el límite numérico en el que la Pérdida de Huber utiliza la aplicación cuadrática de la pérdida o el cálculo lineal.

El componente cuadrático de la Pérdida de Huber caracteriza las ventajas del MSE que penalizan los valores atípicos; dentro de la Pérdida de Huber, ésta se aplica a los errores menores que delta, lo que garantiza una predicción más precisa del modelo.

Supón que el error calculado, que es la diferencia entre los valores reales y los predichos, es mayor que el delta. En ese caso, la Pérdida de Huber utiliza el cálculo lineal de la pérdida similar al MAE, en el que hay menos sensibilidad al tamaño del error para garantizar que el modelo entrenado no penaliza en exceso los errores grandes, especialmente si el conjunto de datos contiene valores atípicos o muestras de datos poco probables.

Funciones de pérdida para la clasificación

Pérdida de entropía cruzada binaria / Pérdida logarítmica

La Pérdida de entropía cruzada binaria (BCE) es una medida de rendimiento de los modelos de clasificación que da como resultado una predicción con un valor de probabilidad normalmente entre 0 y 1, y este valor de predicción corresponde a la probabilidad de que una muestra de datos pertenezca a una clase o categoría. En el caso de la Pérdida de entropía cruzada binaria, hay dos clases distintas. Pero, en particular, una variante de la pérdida de entropía cruzada, la Entropía Cruzada Categórica, se aplica a escenarios de clasificación multiclase.

Para entender la Pérdida de entropía cruzada binaria, a veces llamada Pérdida logarítmica, es útil discutir los componentes de los términos.

• Pérdida: Se trata de una cuantificación matemática del margen/diferencia entre la predicción de un algoritmo de machine learning y el valor objetivo real.
• Entropía: Una definición sencilla de entropía es que es un cálculo del grado de aleatoriedad o desorden dentro de un sistema
• Entropía cruzada: Es un término utilizado habitualmente en la teoría de la información, y mide las diferencias entre dos distribuciones de probabilidad que pueden utilizarse para identificar una observación.
• Binario: Es una expresión de dígitos numéricos que utiliza uno de los dos estados, 0 ó 1. Esto se amplía a la definición de Clasificación Binaria, en la que ditingus=mos dos clases (A y B) utilizando la representación binaria, en la que a la clase A se le asigna la representación numérica de 0 y a la clase B se le asigna 1.

La pérdida de entropía cruzada binaria (o pérdida logarítmica) es una cuantificación de la diferencia entre la predicción de un algoritmo de machine learning y la predicción objetivo real que se calcula a partir del valor negativo de la suma del valor logarítmico de las probabilidades de las predicciones realizadas por el algoritmo de machine learning frente al número total de muestras de datos. La BCE se encuentra en casos de uso de machine learning que son problemas de regresión logística y en el entrenamiento de redes neuronales artificiales diseñadas para predecir la probabilidad de que una muestra de datos pertenezca a una clase y aprovechan internamente la función de activación sigmoidea.

La ecuación matemática de la Pérdida de entropía cruzada binaria, también conocida como pérdida logarítmica, es:

L(y, f(x)) = -[y * log(f(x)) + (1 - y) * log(1 - f(x))]

Donde:

• L representa la función binaria de pérdida de entropía cruzada
• y es la etiqueta binaria verdadera (0 ó 1)
• f(x) es la probabilidad prevista de la clase positiva (entre 0 y 1)

Cuándo utilizar la Pérdida de entropía cruzada binaria / Pérdida logarítmica

La ecuación anterior se aplica específicamente a un escenario en el que el algoritmo de machine learning hará una clasificación entre dos clases. Se trata de un escenario de clasificación binaria.

Como se indica en la ecuación mediante el símbolo negativo '-', el BCE calcula la pérdida determinando el negativo de dos términos y, para varias predicciones o muestras de datos, la media del negativo de los dos términos siguientes:

1. El logaritmo de la probabilidad predicha por el modelo de que la clase positiva esté presente y * log(f(x))
2. El logaritmo de 1 menos la probabilidad prevista de la clase negativa: (1 - y) * log(1 - f(x))

La función de pérdida BCE penaliza las predicciones inexactas, que son las predicciones que tienen una diferencia significativa respecto a la clase positiva o, en otras palabras, tienen una cuantificación elevada de la entropía. Cuando el BCE se utiliza como componente dentro de los algoritmos de aprendizaje, esto anima al modelo a refinar sus predicciones, que son probabilidades para la clase adecuada durante su entrenamiento.

Pérdida de Hinge

La Pérdida de Hinge es una función de pérdida utilizada en machine learning para entrenar clasificadores que optimizan para aumentar el margen entre los puntos de datos y el límite de decisión. De ahí que se utilice principalmente para clasificaciones de margen máximo. Para garantizar el máximo margen entre los puntos de datos y los límites, la Pérdida de Hinge penaliza las predicciones del modelo de machine learning que se clasifican erróneamente, que son las predicciones que caen en el lado equivocado del límite del margen y también las predicciones que se clasifican correctamente pero están muy cerca del límite de decisión.

Esta característica de la función de Pérdida de Hinge garantiza que los modelos de machine learning sean capaces de predecir la clasificación exacta de los puntos de datos a su valor objetivo con una confianza que supere el umbral del límite de decisión. Este enfoque del machine learning mejora la capacidad de generalización del modelo, haciéndolo eficaz para clasificar con precisión puntos de datos con un alto grado de certeza.

La ecuación matemática de la Pérdida de Hinge es:

L(y, f(x)) = max(0, 1 - y * f(x))

Donde:

• L representa la Pérdida de Hinge
• y es la etiqueta verdadera o valor objetivo (-1 o 1)
• f(x) es el valor previsto o la salida de la función de decisión

Elegir la función de pérdida adecuada

Seleccionar la función de pérdida adecuada para aplicarla a un algoritmo de machine learning es esencial, ya que el rendimiento del modelo depende en gran medida de la capacidad del algoritmo para aprender o adaptar sus pesos internos para ajustarse a un conjunto de datos.

El rendimiento de un modelo o algoritmo de machine learning se define por la función de pérdida utilizada, principalmente porque el componente de la función de pérdida afecta al algoritmo de aprendizaje utilizado para minimizar la pérdida de error del modelo o el valor de la función de coste. Esencialmente, la función de pérdida influye en la capacidad del modelo para aprender y adaptar el valor de sus ponderaciones internas para ajustarse a los patrones de un conjunto de datos.

Cuando se selecciona adecuadamente, la función de pérdida permite al algoritmo de aprendizaje converger eficazmente a una pérdida óptima durante su fase de entrenamiento y generalizar bien a muestras de datos no vistas. Una función de pérdida adecuadamente seleccionada actúa como guía, dirigiendo el algoritmo de aprendizaje hacia la precisión y la fiabilidad, asegurándose de que capta los patrones subyacentes en los datos al tiempo que evita el sobreajuste o el infraajuste.

Factores a tener en cuenta al seleccionar una función de pérdida

Comprender el tipo de problema de machine learning que se plantea ayuda a determinar la categoría de función de pérdida que se debe utilizar. Se aplican diferentes funciones de pérdida a diversos problemas de machine learning.

Clasificación vs Regresión

Las tareas de machine learning de clasificación suelen implicar la asignación de puntos de datos a una etiqueta de categoría específica. Con este tipo de tarea de machine learning, la salida del modelo de machine learning suele ser un conjunto de probabilidades que determinan la probabilidad de que un punto de datos sea una determinada etiqueta.

La función de pérdida de entropía cruzada se utiliza habitualmente en tareas de clasificación. En una tarea de regresión de machine learning en la que el objetivo es que un modelo de machine learning produzca una predicción basada en un conjunto de entradas, son más adecuadas las funciones de pérdida como el Error cuadrático medio o el Error medio absoluto.

Clasificación binaria frente a multiclase

La clasificación binaria implica la categorización de muestras de datos en dos categorías distintas, mientras que la clasificación multiclase, como su nombre indica, implica la categorización de muestras de datos en más de dos categorías. Para los problemas de clasificación de machine learning que implican sólo dos clases (clasificación binaria), lo mejor es aprovechar una función de pérdida de entropía cruzada binaria. En situaciones en las que más de dos clases son objetivos de las predicciones, debe utilizarse la entropía cruzada categórica.

Sensibilidad

Otro factor a tener en cuenta es la sensibilidad de la función de pérdida a los valores atípicos. En algunos casos, es deseable garantizar que los valores atípicos y las muestras de datos que sesgan la distribución estadística general del conjunto de datos se penalicen durante el entrenamiento; en tales casos, son adecuadas las funciones de pérdida como el error cuadrático medio.

Mientras que hay escenarios en los que se requiere menos sensibilidad a los valores atípicos, éstos son escenarios en los que los valores atípicos podrían ser "sucesos nunca ocurridos" o poco probables. Para este objetivo, penalizar los valores atípicos podría producir un modelo no eficaz. Una función de pérdida como el error medio absoluto es aplicable en estos casos. Para obtener lo mejor de ambos mundos, los profesionales deberían considerar la función de pérdida de Huber, que toma componentes que penalizan los valores atípicos con valores de error bajos y reducen la sensibilidad del modelo a los valores atípicos con valores de error grandes.

Eficacia informática

Los recursos informáticos son una mercancía en el ámbito del machine learning, comercial y de investigación. El acceso a una gran capacidad informática permite a los profesionales la flexibilidad necesaria para experimentar con grandes conjuntos de datos y resolver problemas de machine learning más complejos. Algunas funciones de pérdida son más exigentes computacionalmente que otras, sobre todo cuando el número de conjuntos de datos es grande. Esto hace que la eficiencia computacional de una función de pérdida sea un factor a tener en cuenta durante el proceso de selección de una función de pérdida.

Impacto de los valores atípicos y de la distribución de los datos

Los valores atípicos son muestras de datos que se salen de la distribución estadística general de un conjunto de datos; a veces se denominan anomalías o irregularidades. El modo en que se gestionan los valores atípicos determina el rendimiento y la precisión del modelo de machine learning entrenado.

Como ya se ha dicho, los valores atípicos en los conjuntos de datos afectan a los valores de error utilizados en las funciones de pérdida, dependiendo de la función de pérdida utilizada. El efecto de los valores atípicos en las funciones de pérdida se propaga al resultado del proceso de aprendizaje del algoritmo de machine learning, lo que puede provocar un comportamiento intencionado o no intencionado del algoritmo o modelo de machine learning.

Por ejemplo, el error cuadrático medio penaliza los valores atípicos que contribuyen a grandes valores/términos de error; esto significa que durante el proceso de entrenamiento, los pesos del modelo se ajustan para aprender a acomodar estos valores atípicos. De nuevo, si éste no es el comportamiento previsto del modelo de machine learning, el modelo final creado tras el entrenamiento tendrá una escasa generalización a los datos no vistos. Para escenarios en los que se requiere mitigar el impacto de los valores atípicos, son más aplicables funciones como la MAE y la pérdida de Huber.

Implementación de las funciones de pérdida

Ejemplos de aplicación de funciones de pérdida habituales

Implementación del MAE en Python

# Python implementation of Mean Absolute Error (MAE)

def mean_absolute_error(actual:list, predicted:list) -> float:
    """
    Calculate the Mean Absolute Error between actual and predicted values

    :param actual: list, actual values
    :param predicted: list, predicted values
    :return: float, the calculated MAE
    """
    # Ensure the length of the two lists are the same
    if len(actual) != len(predicted):
        raise ValueError("The length of actual values and predicted values must be the same")

    # Calculate the absolute differences
    absolute_diffs = [abs(act - pred) for act, pred in zip(actual, predicted)]
    
    # Calculate the mean of the absolute differences
    mae = sum(absolute_diffs) / len(actual)
    
    return mae

# Example usage:
# actual values
y_true = [3, -0.5, 2, 7]

# predicted values
y_pred = [2.5, 0.0, 2, 8]

# Calculate MAE
mae_value = mean_absolute_error(y_true, y_pred)
print(mae_value)
# 0.5

Implementación de MSE en Python

# Python implementation of Mean Squared Error (MSE) / L2 Loss

def mean_squared_error(actual:list, predicted:list) -> float:
    """
    Calculate the Mean Squared Error between actual and predicted values

    :param actual: list, actual values
    :param predicted: list ,predicted values
    :return: float, the calculated MSE
    """
    # Ensure the length of the two lists are the same
    if len(actual) != len(predicted):
        raise ValueError("The length of actual values and predicted values must be the same")

    # Calculate the squared differences
		# (yᵢ - ȳ)²
    squared_diffs = [(act - pred) ** 2 for act, pred in zip(actual, predicted)]
    
    # Calculate the mean of the squared differences
    mse = sum(squared_diffs) / len(actual)
    
    return mse

# Example usage:
# actual values
y_true = [1, 2, 3, 4, 5]

# predicted values
y_pred = [1.1, 2.2, 2.9, 4.1, 4.9]

# Calculate MSE
mse_value = mean_squared_error(y_true, y_pred)
print(mse_value)
# 0.015999999999999993

El uso de bibliotecas para la implementación de la función de pérdida

Aunque la implementación personalizada de funciones de pérdida es factible, y bibliotecas de aprendizaje profundo como TensorFlow y PyTorch admiten el uso de funciones de pérdida a medida en implementaciones de redes neuronales, bibliotecas como Scikit-learn, TensorFlow y PyTorch ofrecen implementaciones integradas de funciones de pérdida de uso común.

Estas funcionalidades preintegradas facilitan el aprovechamiento y abstraen las complejidades que conlleva la implementación de estas funciones de pérdida, agilizando el proceso de desarrollo de modelos de machine learning.

Utilizar estas bibliotecas de aprendizaje profundo proporciona ventajas sobre las implementaciones en Python puro, algunas de las cuales son:

• Facilidad de uso
• Eficacia y optimización
• Soporte de GPU y computación paralela
• Apoyo de la comunidad de desarrolladores

Error medio absoluto (MAE) utilizando la biblioteca scikit-learn

from sklearn.metrics import mean_absolute_error

# actual values
y_true = [3, -0.5, 2, 7]

# predicted values
y_pred = [2.5, 0.0, 2, 8]

# Calculate MAE using scikit-learn
mae_value = mean_absolute_error(y_true, y_pred)
print(mae_value)
#0.5

Error cuadrático medio (ECM) utilizando la biblioteca scikit-learn

from sklearn.metrics import mean_squared_error

# actual values
y_true = [1, 2, 3, 4, 5]

# predicted values
y_pred = [1.1, 2.2, 2.9, 4.1, 4.9]

# Calculate MSE using scikit-learn
mse_value = mean_squared_error(y_true, y_pred)
print(mse_value)
# 0.016

Conclusión

En resumen, elegir la función de pérdida adecuada es crucial para un entrenamiento eficaz del modelo de machine learning. Este artículo destaca las principales funciones de pérdida, su papel en los algoritmos de machine learning y su idoneidad para distintas tareas. Desde el Error cuadrático medio (ECM) a la Pérdida de Huber, cada función tiene sus ventajas únicas, ya sea para tratar los valores atípicos o para equilibrar el sesgo y la varianza.

La decisión de utilizar funciones de pérdida personalizadas o preconstruidas de bibliotecas como Scikit-learn, TensorFlow y PyTorch depende de las necesidades específicas del proyecto, la eficiencia computacional y la experiencia del usuario. Estas bibliotecas ofrecen facilidad de implantación, apoyo continuo de la comunidad y actualizaciones periódicas.

A pesar de la evolución del machine learning, la importancia de las funciones de pérdida permanece constante. Las tendencias futuras pueden traer funciones de pérdida más especializadas, pero los principios fundamentales probablemente persistirán. Para profundizar en el machine learning y sus aplicaciones, explora el programa Científico de Machine Learning con Python de DataCamp.