Estructuras de datos: Una guía completa con ejemplos en Python

Las estructuras de datos existen tanto en el mundo digital como en el físico. Un diccionario es un ejemplo físico de una estructura de datos en la que los datos comprenden definiciones de palabras organizadas por orden alfabético dentro de un libro. Esta organización permite una consulta específica: dada una palabra, se puede buscar su definición.

En esencia, una estructura de datos es un método de organización de datos que facilita determinados tipos de consultas y operaciones sobre esos datos.

Empezaremos cubriendo las estructuras de datos lineales como matrices, listas, colas y pilas. A continuación, volveremos atrás para explicar la diferencia entre estructuras lineales y no lineales, antes de sumergirnos en las tablas hash, los árboles y los grafos.

Si quieres aprender más, consulta este curso sobre estructuras de datos y algoritmos en Python.

Matrices

Las matrices son estructuras de datos fundamentales ampliamente disponibles en todos los lenguajes de programación. Permiten almacenar un número fijo (N) de valores de forma secuencial en la memoria.

Los elementos de la matriz se indexan desde el primer elemento en el índice (0) hasta el último elemento en el índice (N-1).

Permiten realizar las siguientes operaciones:

1. Lee el valor en un índice dado.
2. Actualiza el valor en un índice dado.
3. Iterar sobre todos los valores almacenados.
4. Obtén el tamaño de la matriz.

Las matrices son muy eficaces en situaciones en las que el número de valores que hay que almacenar se conoce de antemano, y las operaciones principales consisten en leer y escribir datos en índices concretos.

Imagina que necesitas almacenar las lecturas diarias de temperatura del mes de diciembre. Puede que quieras permitir a los usuarios recuperar la temperatura de un día concreto y realizar diversos análisis estadísticos de las temperaturas a lo largo del mes.

Como se sabe de antemano que el número de días de diciembre es 31, las matrices son una opción excelente para almacenar las lecturas de temperatura. Inicialmente, se crearía una matriz con 31 posiciones vacías. Entonces, tras obtener cada lectura de temperatura, la temperatura de un día determinado se asignaría al índice de matriz correspondiente: el día 1 se almacenaría en el índice 0, el día 2 en el índice 1, y así sucesivamente, hasta el día 31, que se almacenaría en el índice 30.

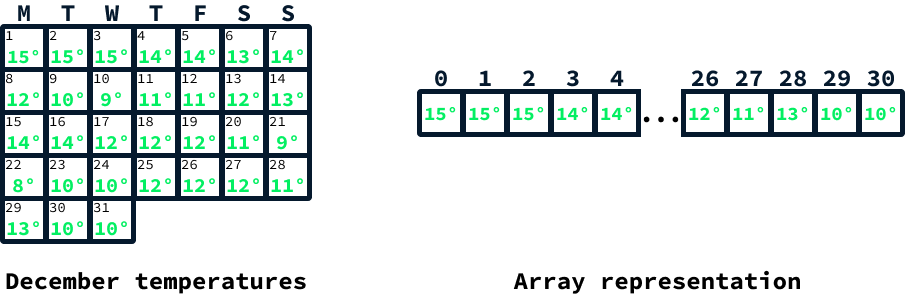
Acceder al índice correspondiente permite recuperar la temperatura de un día concreto. Las estadísticas, como la temperatura media, pueden determinarse iterando sobre todos los elementos, manteniendo una suma acumulada y dividiendo después por el tamaño de la matriz.

Las matrices no están disponibles de forma nativa en Python. Se utilizan entre bastidores como estructura subyacente de varios tipos de datos, pero no se admiten directamente en el lenguaje. Para utilizar matrices explícitamente, se pueden utilizar bibliotecas como array, que ofrecen una implementación de matrices. Sin embargo, a menudo es más práctico utilizar una lista con un tamaño fijo en situaciones en las que podría ser necesaria una matriz. Las listas ofrecen flexibilidad y son una parte esencial de la funcionalidad de Python, como veremos a continuación.

Podemos crear una lista para simular una matriz de 31 elementos, cada uno inicializado a Ninguno, utilizando [None] * 31. Aquí, None indica que todavía no se ha registrado ninguna lectura de temperatura.

december_temperatures = [None] * 31

Para fijar el valor en un índice concreto, utilizamos december_temperatures[index], donde index es un número comprendido entre 0 y 30. Por ejemplo, para registrar la temperatura del primer día (almacenada en el índice 0), lo haríamos así:

december_temperatures[0] = 15

Acceder a una temperatura es igualmente sencillo, utilizando december_temperatures[index].

print(december_temperatures[0])

15

Listas

Imagina ahora que, en lugar de centrarnos en diciembre, instalamos un sensor en algún lugar para tomar lecturas periódicas de la temperatura durante un periodo indeterminado. En este caso, utilizar una matriz no es la mejor opción, ya que podríamos quedarnos sin espacio debido a su tamaño fijo en el momento de la creación.

Una estructura de datos más adecuada en este caso sería una lista. Hay dos tipos de listas:

• Listas de matrices
• Listas enlazadas

Listas de matrices

Las listas de matrices pueden considerarse una versión más flexible de las matrices. Pueden realizar todas las funciones de las matrices, pero también añadir nuevos valores, por lo que su tamaño no es fijo al crearse. Las listas de matrices se corresponden con el uso de list() en Python.

Su implementación se basa en utilizar una matriz que se expande cuando se agota el espacio, de ahí el nombre de lista de matrices. Sin embargo, como hemos aprendido antes, las matrices no pueden crecer, así que ¿cómo es posible?

Cuando la matriz subyacente de una lista de matrices está llena y queremos añadir un nuevo valor, se crea una matriz mayor bajo el capó. Todos los valores anteriores se copian en esta nueva matriz más grande. A continuación, el nuevo valor se añade en la primera posición disponible de la nueva matriz.

Imagina que queremos añadir el valor 71 a esta matriz:

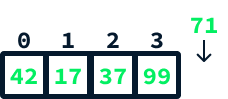
Esto puede hacerse así:

La cantidad de espacio nuevo asignado cada vez que realizamos esta operación es crucial para el rendimiento de la lista de matrices. Si, en cada adición, creáramos una matriz con sólo una nueva posición para el nuevo valor que se añade, significaría que cada operación de adición requeriría copiar la totalidad de los datos preexistentes. Esto sería extremadamente ineficaz: imagínate tener que copiar millones de registros simplemente para añadir uno nuevo.

En cambio, la estrategia habitual es duplicar el tamaño de la matriz cada vez que se necesita más espacio. Se puede demostrar que este enfoque anula el efecto de tener estos pasos de copia adicionales a lo largo del tiempo.

Para añadir elementos a una lista Python, utilizamos el método .append(). Aquí tienes un ejemplo de cómo crear una lista vacía y añadirle una lectura de temperatura:

temperatures = []
temperatures.append(35)

Listas enlazadas

Para estructurar los datos en un ordenador, necesitamos una forma de relacionar los valores entre sí. Las matrices lo consiguen asignando posiciones de memoria contiguas -es decir, posiciones de memoria directamente contiguas- y almacenando valores secuencialmente. Piénsalo como una hilera de casas en una calle: cada casa tiene una dirección única (índice), y están físicamente situadas una junto a otra.

Sin embargo, éste no es el único método para organizar los datos. Una alternativa consiste en utilizar una estructura basada en nodos.

Un nodo es un objeto que almacena un valor junto con referencias a otros nodos. Por ejemplo, para crear una estructura similar a una lista utilizando nodos, podemos tener un nodo que contenga tanto un valor como una referencia al siguiente elemento de la lista. En Python, esto puede implementarse con una clase:

class Node:
    def __init__(self, value, next_node):
        self.value = value
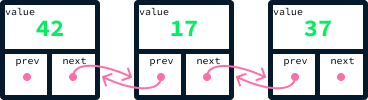
        self.next_node = next_node

Utilizando este enfoque, se puede crear una lista enlazando valores mediante la referencia next_node. Aquí tienes un fragmento de código que crea una lista con los valores 42, 17, y 37:

node_37 = Node(37, None) # There's no node after 37 so next_node is None
node_17 = Node(17, node_37)
node_42 = Node(42, node_17)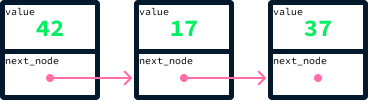

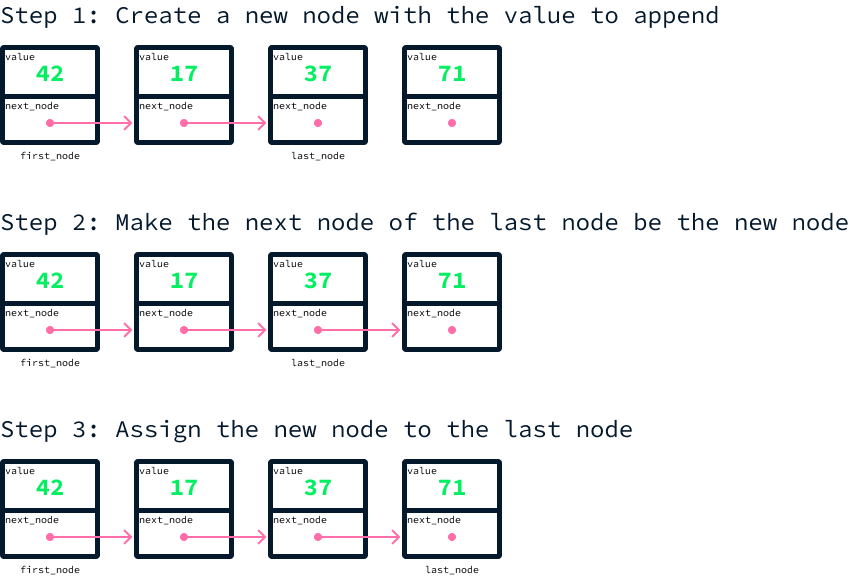
Enlazar manualmente los nodos de esta manera no es práctico. La implementación real requiere crear otra clase que mantenga referencias tanto al primer como al último nodo de la lista. Para añadir un nuevo valor, hacemos lo siguiente

1. Crea un nodo con el valor deseado.
2. Establece este nuevo nodo como nodo siguiente del último nodo actual.
3. Actualiza la referencia del último nodo a este nuevo nodo añadido.

Imagina que queremos añadir el valor 71 a nuestra matriz de ejemplo:

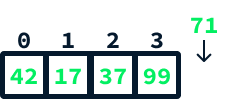
Esto puede hacerse así:

class LinkedList:
    def __init__(self):
        self.first_node = None
        self.last_node = None

    def append(self, value):
        node = Node(value, None)
        if self.first_node is None:
            self.first_node = node
            self.last_node = node
        else:
            self.last_node.next_node = node
            self.last_node = node

A diferencia de las listas de matrices, no podemos acceder directamente a los valores por sus índices. Para leer un valor concreto en un índice, debemos empezar por el primer nodo y pasar secuencialmente de un nodo al siguiente hasta llegar al índice deseado. Este proceso es significativamente más lento que el acceso directo. Si tenemos millones de valores almacenados en la lista, tendríamos que leer millones de valores en memoria para llegar a un índice concreto.

La ventaja de una lista enlazada radica en que podemos añadir y eliminar instantáneamente elementos de la parte anterior o posterior de la lista. Esta capacidad abre la posibilidad de implementar dos nuevas estructuras de datos: las colas y las pilas, de las que hablaremos a continuación.

Colas

Imagina que estás desarrollando una aplicación para restaurantes que registra los pedidos de los clientes y los envía a la cocina. Cuando los clientes lleguen al restaurante, harán cola para hacer sus pedidos, esperando ser atendidos en la secuencia de su llegada. Esto significa que el primer cliente de la cola debe recibir su pedido el primero, y el último, el último.

En la cocina, el chef prefiere centrarse en un pedido cada vez, por lo que la aplicación sólo debe mostrar el pedido actual. Una vez preparado y enviado un pedido, debe aparecer el siguiente pedido en la cola.

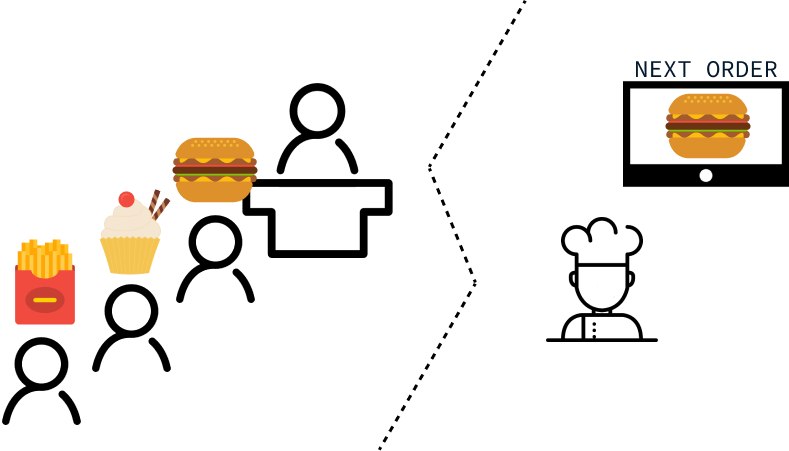
Podemos interpretar los requisitos anteriores como la necesidad de una estructura de datos que admita las siguientes operaciones:

1. Añadir elementos.
2. Visualizar el elemento que se ha añadido primero.
3. Eliminar el elemento que se ha añadido primero.

Estas operaciones son precisamente lo que ofrece una cola. Una cola puede implementarse utilizando una lista enlazada, en la que los elementos se añaden agregándolos a la lista. Como los elementos se ordenan por su hora de llegada, el primer nodo es siempre el que debe ser servido a continuación.

Así es como se almacenarían en la cola los pedidos anteriores:

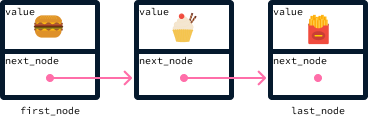
Una vez que una orden está lista, se puede eliminar actualizando el primer elemento a su next_node, suponiendo que haya un nodo posterior. El nuevo primer nodo se convierte en el segundo nodo:

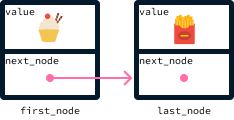
Las colas se describen como una estructura de datos FIFO ( primero en entrar, primero en salir ), porque el primer elemento que se añade es también el primero que se elimina. En nuestro ejemplo del restaurante, el primer cliente en llegar es también el primero en ser servido (y eliminado de la lista del chef).

Para utilizar una cola en Python, podemos utilizar la coleccióndeque del módulo collections. Importa este módulo y crea una cola vacía como se muestra a continuación:

from collections import deque
orders = deque()

Añadir un nuevo elemento al final de la cola puede conseguirse utilizando el método.append():

orders.append("burger")
orders.append("sunday")
orders.append("fries")

Para recuperar y eliminar el siguiente pedido de la parte delantera de la cola, utilizamos el método.popleft():

orders.append("burger")
orders.append("sunday")
orders.append("fries")

burger
sunday
fries

Pilas

En determinadas situaciones, deseamos lo contrario del comportamiento de una cola: más bien queremos rastrear el elemento añadido más recientemente.

Para ejemplificarlo, imagina que te encargan añadir una función de deshacer a un editor de imágenes. Esto requiere un método para controlar las acciones del usuario, que proporcione acceso a las operaciones más recientes. Esto se debe a que las funcionalidades de deshacer suelen invertir las acciones empezando por la última realizada y avanzando hacia la primera.

Una pila es exactamente una estructura de datos que admite estas operaciones:

1. Añadir elementos.
2. Visualizar el último elemento añadido.
3. Eliminar el último elemento añadido.

Al igual que las colas, las pilas también pueden implementarse utilizando una lista enlazada. Añadir un elemento se sigue haciendo añadiendo el elemento a la lista. Sin embargo, nuestro interés se desplaza al último elemento de la lista en lugar de al primero. Para recuperar el elemento más reciente, buscamos el último elemento de la lista. Para eliminar el último elemento es necesario que borremos el último elemento.

En nuestra estructura de nodos, sólo rastreamos el nodo siguiente. Para facilitar la eliminación del último elemento, necesitamos acceder al elemento que le precede, eliminar su nodo_siguiente y promover ese nodo para que sea el último. Podemos conseguirlo modificando la estructura de nodos para que rastree también el nodo anterior de cada nodo. Una lista enlazada de este tipo se denomina lista doblemente enlazada.

Las pilas se describen como una estructura de datos de último en entrar, primero en salir (LIFO), porque el último elemento que se añade es también el primero que se elimina.

Para utilizar una pila en Python, podemos utilizar la misma coleccióndeque . Utilizamos el método.append() para añadir nuevos elementos:

from collections import deque
actions = deque()

actions.append("crop")
actions.append("desaturate")
actions.append("resize")

Para recuperar y eliminar la siguiente orden de la parte superior de la pila, utilizamos el método.pop():

print(actions.pop())
print(actions.pop())
print(actions.pop())

resize
desaturate
crop

Lineal vs. Estructuras de datos no lineales

Hasta ahora, hemos explorado cinco estructuras de datos: matrices, listas de matrices, listas enlazadas, colas y pilas. Cada una de ellas es una estructura de datos lineal porque sus elementos están ordenados en una secuencia, en la que cada elemento tiene un elemento anterior y un elemento siguiente claros.

A continuación, nos centraremos en las estructuras de datos no lineales. A diferencia de los tipos lineales, estas estructuras no organizan los elementos unos junto a otros de forma lineal. En consecuencia, no tienen una noción definida de los elementos anterior y siguiente. En su lugar, establecen distintos tipos de relaciones entre los elementos.

Esta característica los hace especialmente adecuados para ejecutar consultas especializadas sobre los datos con gran eficacia, en lugar de servir simplemente como medio de almacenamiento de datos en memoria.

Tablas hash

Empezamos este artículo hablando de un ejemplo real de estructura de datos: los diccionarios. Resulta que organizar los datos de modo que puedan buscarse por un campo concreto (por ejemplo, buscar una definición dada de una palabra) es extremadamente útil en general, así que los informáticos también inventaron una estructura de datos que lo permite.

Para entender esta estructura de datos, vamos a ver cómo podemos crear un diccionario virtual, es decir, una estructura de datos en la que podamos:

1. Añade una palabra en su definición.
2. Dada una palabra, busca su definición.

Recuerda el ejemplo de registrar las temperaturas durante todo el mes de diciembre. Utilizamos una matriz con 31 elementos correspondientes a cada día del mes para almacenar las temperaturas en sus respectivos índices. Este enfoque permite buscar eficazmente la temperatura de un día determinado.

Este escenario es similar a tratar con pares de datos (day, temperature), donde el objetivo es recuperar el temperature especificando el día. Del mismo modo, en el caso de los diccionarios, manejamos pares de datos (word, definition) y pretendemos encontrar el definition cuando se nos proporciona un word.

Estos pares se denominan pares clave-valor o entradas. La clave es el parámetro utilizado en la consulta de búsqueda, y el valor es el resultado de esa consulta.

Lo que nos impide utilizar una matriz para el problema del diccionario es que nuestras claves son cadenas en lugar de números. Con claves numéricas, podemos utilizar directamente una matriz para asociar claves y valores, colocando los valores en sus índices correspondientes.

Para resolver este problema, primero tenemos que convertir las palabras en números. Una función que realiza esta conversión se denomina función hash. Existen numerosos enfoques para crear una función de este tipo. Por ejemplo, podríamos asignar valores numéricos a las letras, con a como 1, b como 2, c como 3, y así sucesivamente, y luego sumar estos valores.

Por ejemplo, la palabra data se calcularía como 4 + 1 + 20 + 1 = 26. Sin embargo, esta función tiene sus inconvenientes, de los que hablaremos en breve. Los detalles sobre cómo idear una función hash eficaz están más allá del propósito de este artículo, pero Python proporciona convenientemente una función hash() que se encarga eficazmente de esta tarea por nosotros.

hash("data")

-6138587229816301269

En el ejemplo anterior, habrás observado que la función hash produjo un número negativo. Es importante tener en cuenta que los índices positivos de las matrices van de 0 a N - 1. Una vez convertidas las claves en números, podemos asignarlas al intervalo de 0 a N - 1 mediante el operador de módulo % (que da como resultado el resto de una división; por ejemplo, 10 % 3 da como resultado 1).

Como nota al margen, la función hash() de Python puede devolver valores diferentes en distintas ejecuciones del programa. Sólo es determinista dentro de la misma ejecución del programa, lo que significa que puedes observar diferentes valores hash para el mismo objeto si ejecutas tu programa varias veces.

Considera una matriz que contiene 100 elementos. Para localizar el índice correspondiente a la cadena "data", procedemos del siguiente modo:

hash("data") % 100

31

La estructura de datos de la tabla hash es esencialmente una gran matriz que almacena pares clave-valor en índices determinados aplicando una función hash a las claves.

Por limitaciones de espacio, el diagrama anterior sólo incluye la abreviatura "def" para representar la definición. Sin embargo, en la práctica, el segundo elemento de cada entrada sería la definición completa de la palabra.

Hay otro aspecto importante a tener en cuenta. Dado que hay bastante más de 100 palabras, si seguimos añadiendo palabras, las palabras distintas darán inevitablemente el mismo valor hash. Para solucionarlo, en lugar de limitar cada elemento de la matriz a un único par clave-valor, empleamos una lista enlazada para almacenar todas las entradas que comparten el mismo valor hash.

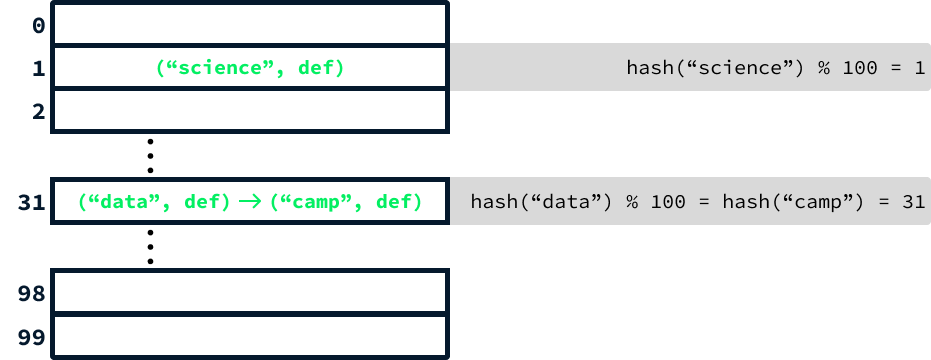
Cuando dos entradas generan el mismo hash, se habla de colisión. Este escenario modifica ligeramente el proceso de búsqueda. Tras calcular el código hash, es necesario recorrer la lista para localizar la entrada correcta. Aunque este enfoque ralentiza la operación de búsqueda, puede demostrarse que utilizando un tamaño inicial de matriz suficientemente grande (mayor de 100) y una función hash bien diseñada se puede mitigar significativamente el impacto de las colisiones. En consecuencia, la eficacia sigue siendo casi equivalente a la de un conjunto.

Para una función hash diseñada eficazmente, debería ser raro encontrar valores distintos que den como resultado el mismo hash. Por eso no es ideal una función hash simplista que se limite a sumar los valores numéricos de los caracteres de una palabra. Dos palabras compuestas por las mismas letras, independientemente de su orden, producirían códigos hash idénticos. Por ejemplo, "escuchar" y "silencio" producirían el mismo hash. En cambio, la función hash incorporada que proporciona Python es mucho más robusta y está diseñada específicamente para minimizar las colisiones.

Las tablas hash son posiblemente la estructura de datos más importante que existe. Son extremadamente eficaces y versátiles. En Python, se implementan a través de la clase dict(). Debido a su parecido con un diccionario, en Python, la estructura de datos se llama en realidad diccionario en lugar de tabla hash.

Para simplificar, nuestro ejemplo se centra en añadir y buscar entradas. En general, los diccionarios ofrecen más flexibilidad y admiten operaciones adicionales, incluida la eliminación. Para crear un diccionario vacío (tabla hash) en Python, puedes utilizar {} de la siguiente manera:

word_definitions = {}
word_definitions["data"] = "Facts or information."

Puedes acceder a la definición de una palabra utilizando la palabra como clave, así:

print(word_definitions["data"])

Facts or information.

Árboles

Imagina que estás desarrollando un sitio web para una agencia inmobiliaria. Tu tarea consiste en crear una función que permita a los usuarios filtrar los anuncios por precio. La función debe permitir a los usuarios

1. Encuentra el anuncio más barato.
2. Encuentra el anuncio más caro.
3. Encuentra todos los anuncios por debajo de un precio determinado.

Normalmente, este proceso implica recorrer todos los listados de casas y filtrar las que quedan fuera del rango de precios deseado. Sin embargo, nuestro objetivo es desarrollar una solución que se amplíe de forma más eficiente, que no requiera examinar todo el conjunto de datos para encontrar listados relevantes. Los árboles son la estructura de datos perfecta para responder a este tipo de consulta.

Los árboles son estructuras de datos basadas en nodos, como las listas enlazadas. Sin embargo, en lugar de tener referencias anterior y siguiente, cada nodo conservará un valor y dos referencias: un nodo izquierdo y un nodo derecho.

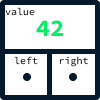
En nuestro ejemplo de web de agencia inmobiliaria, cada nodo representará un anuncio de propiedad. Para optimizar las consultas relacionadas con los precios, estableceremos una regla: los listados con precios más bajos se almacenarán siempre a la izquierda de un nodo, mientras que los listados con precios más altos se almacenarán siempre a la derecha.

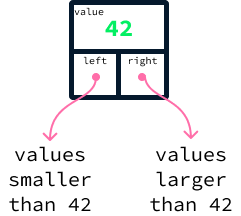
Para un ejemplo concreto, considera el siguiente árbol que contiene los valores 42, 17, 73, 4, 22, y 89.

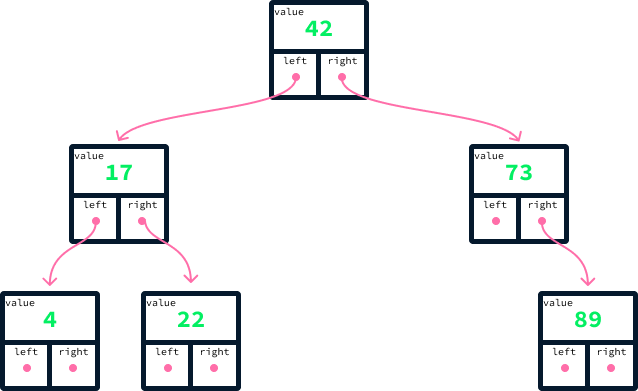
Para cada nodo, todos los de la izquierda tienen valores menores, y todos los de la derecha tienen valores mayores. Un árbol que satisface esta propiedad se denomina árbol de búsqueda binario (BST). Es binario porque cada nodo se refiere como máximo a otros dos nodos, llamados hijos. La parte de búsqueda del término proviene del hecho de que la propiedad de ordenación de los hijos izquierdo y derecho permitirá buscar en el árbol de forma eficaz.

Ya podemos ver cómo un BST ayuda a encontrar rápidamente los listados más baratos y más caros. Debido a la ordenación de los valores, el más barato es siempre el nodo situado más a la izquierda, y el más caro es siempre el nodo situado más a la derecha.

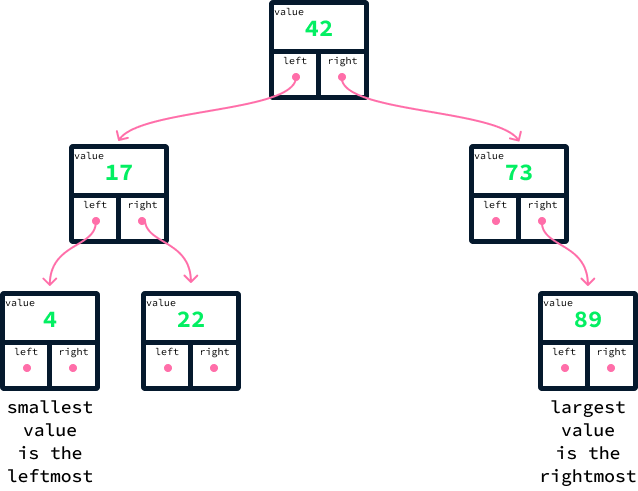
Esto implica que podemos localizarlos sin examinar la mayoría de los datos. Empezando por el nodo superior, también llamado nodo raíz, seguimos sistemáticamente los enlaces de la izquierda para identificar el mínimo y los enlaces de la derecha para identificar el máximo. Esto significa que sólo hay que inspeccionar los nodos a lo largo de la ruta que conecta la raíz con los nodos mínimo y máximo, respectivamente.

Imagina que queremos encontrar todos los nodos con un valor de al menos 50. Estos son los pasos que podemos dar para conseguirlo:

• Empezando por la raíz, comparamos nuestro objetivo, 50, con el valor de la raíz, que es 42.
• Observando que 50 es mayor, entendemos que la raíz y todos los nodos a su izquierda contienen valores menores. En consecuencia, podemos hacer caso omiso de ellos.
• A continuación, pasamos al nodo situado a la derecha de la raíz, que es 73. Si comparamos, vemos que 50 es menor que 73. Esto indica que todos los nodos a la derecha del nodo 73 cumplen nuestros criterios.
• Sin embargo, como 73 no tiene un hijo izquierdo, nuestra búsqueda concluye ahí.

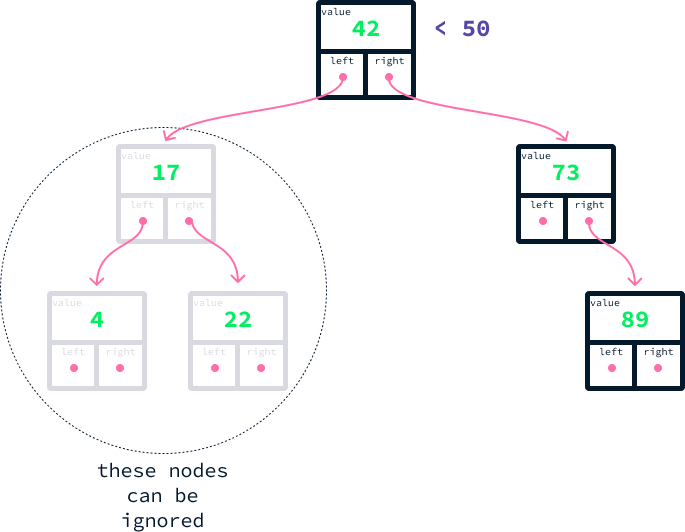
Ya podemos ver cómo los BST pueden acelerar considerablemente las consultas. Incluso en este pequeño ejemplo, evitamos examinar la mitad de los datos.

Generalmente, identificar todos los nodos de un BST que se ajustan a un rango determinado requiere inspeccionar varios nodos cercanos al número de resultados de la consulta. Esto supone una gran ventaja en comparación con tener que inspeccionar cada punto de datos. Imagina que tienes 1.000.000 de listados y una consulta que sólo da 10 resultados. Utilizando una lista, habría que inspeccionar un millón de listados para filtrar los que no se ajustan al rango. Con un BST, sólo hay que inspeccionar unos 10 listados. Esto representa un factor de aceleración de 100.000.

La eficacia de un BST depende en gran medida del equilibrio del árbol. Si añadimos los mismos valores que antes, de menor a mayor-4, 17, 22, 42, 73, seguido de 89-podríamos acabar con un árbol desequilibrado, como se muestra:

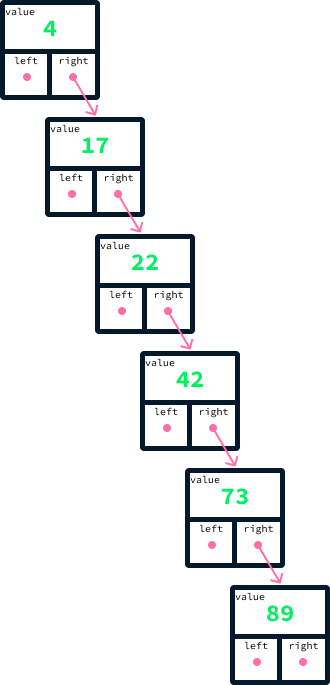
Recordemos que, para encontrar el valor máximo en un BST, empezamos en la raíz y rastreamos los enlaces de la derecha hasta llegar a un nodo que no lo tenga. En el caso de un árbol desequilibrado, como el ilustrado en el diagrama anterior, este proceso requiere examinar cada uno de los nodos. Lo ideal es que los nodos se distribuyan uniformemente entre los lados izquierdo y derecho. Explicar los detalles de cómo se puede conseguir este equilibrio de forma coherente queda fuera del alcance de este artículo. Un tipo de árbol de búsqueda binario conocido por mantener dicho equilibrio se denomina árbol AVL.

El paquete avltree proporciona una implementación de un árbol AVL. El fragmento de código siguiente muestra cómo podemos utilizarlo en este conjunto de datos de listados de casas, un subconjunto depurado de este Conjunto de datos inmobiliarios de EE.UU.

import csv
from avltree import AvlTree as Tree

# Load the listings CSV data
with open("listings.csv", "rt") as f:
    reader = csv.reader(f)
    listings = list(reader)

# Create the tree based on the price column (column index 2)
tree = Tree()
for listing in listings[1:]:
    price = float(listing[2])
    tree[price] = listing

# Display the cheapest listing price
print("Cheapest:", tree.minimum())

# Display the most expensive listing price
print("Most expensive:", tree.maximum())

# Display the number of listings whose price is between 100,000 and 110,000
listings_in_range = list(tree.between(100000, 110000))
print("Num listings between 100000 and 110000:", len(listings_in_range))

Cheapest: 50017.0
Most expensive: 19999900.0
Num listings between 100000 and 110000: 403

Primero utilizamos el módulocsv para leer el conjunto de datos listings.csv. A continuación, creamos un árbol AVL basado en la columna del precio. A continuación, utilizamos los métodos minimum(), maximum() y between() para determinar el precio mínimo, el precio máximo y el número de anuncios cuyo precio oscila entre 100.000 y 110.000 $.

Gráficos

La última estructura de datos que trataremos en este artículo es el gráfico.

Supongamos que estás analizando datos de una plataforma de redes sociales. Estos datos comprenden una lista de usuarios y las amistades entre ellos, y tu objetivo es identificar comunidades dentro de la red social. Aunque el concepto de comunidad puede definirse de varias formas, generalmente se refiere a un grupo de usuarios que tienen un número significativo de amistades dentro de ese grupo.

Los grafos son la estructura de datos ideal para representar datos cuando tenemos entidades y relaciones entre pares de estas entidades. En nuestro ejemplo, las entidades son usuarios, y las relaciones son sus amistades.

Los grafos son estructuras basadas en nodos. Sin embargo, a diferencia de las listas enlazadas y los árboles, que presentan conexiones lineales o jerárquicas entre nodos, un grafo permite que cualquier nodo se conecte con otros múltiples nodos. Estas conexiones entre nodos, llamadas aristas, indican las relaciones entre ellos.

En nuestro ejemplo de red social, cada usuario puede visualizarse como un nodo. Se puede trazar una arista entre dos nodos para denotar una amistad entre los usuarios correspondientes.

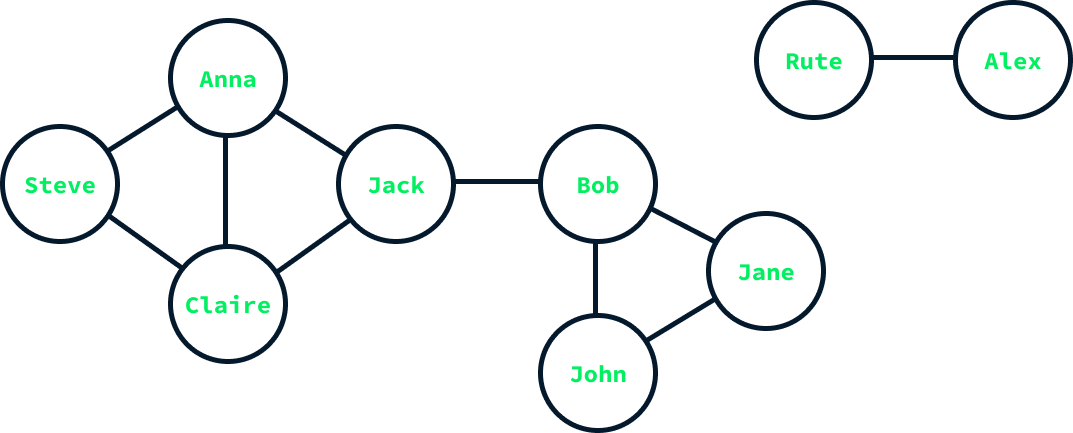
El diagrama anterior ilustra un gráfico que representa las amistades dentro de una pequeña red social. Los nodos representan a los usuarios y están etiquetados con sus nombres, mientras que las aristas representan las amistades. Por ejemplo, Anna es amiga de Steve, Claire y Jack, lo que significa que hay aristas que conectan su nodo con los nodos de estos individuos.

Entre las operaciones que debe admitir una estructura de datos de grafos se incluyen:

1. Añadir un nuevo nodo.
2. Conectar dos nodos con una arista.
3. Recuperar todos los nodos conectados a un nodo concreto.

Una forma habitual de implementar un grafo es utilizar una tabla hash y listas. Se crea una tabla hash con una entrada por cada nodo. La clave de cada entrada es el nodo, y el valor es una lista que contiene todos los nodos a los que está conectado ese nodo.

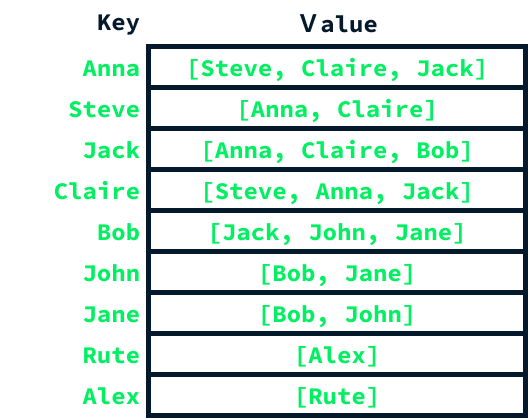
El paquetenetworkx ofrece una implementación de Python para crear y manipular gráficos. Además, la biblioteca networkx abarca una amplia gama de algoritmos de grafos, incluidos los de detección de comunidades. Utilicémoslo para construir el gráfico mencionado anteriormente y apliquemos un algoritmo de detección de comunidades prevalentes para observar los resultados.

Para iniciar la creación del grafo, empezamos importando la biblioteca networkx e inicializando un grafo vacío:

import networkx as nx
G = nx.Graph()

Los nodos pueden añadirse utilizando el métodoadd_node() .

G.add_node("Anna")
G.add_node("Steve")
G.add_node("Jack")
G.add_node("Claire")
G.add_node("Bob")
G.add_node("Jane")
G.add_node("John")
G.add_node("Rute")
G.add_node("Alex")

Los bordes pueden añadirse utilizando el métodoadd_edge() .

G.add_edge("Anna", "Steve")
G.add_edge("Anna", "Jack")
G.add_edge("Anna", "Claire")
G.add_edge("Steve", "Claire")
G.add_edge("Claire", "Jack")
G.add_edge("Jack", "Bob")
G.add_edge("Bob", "John")
G.add_edge("Bob", "Jane")
G.add_edge("John", "Jane")
G.add_edge("Rute", "Alex")

Con nuestro gráfico creado, podemos calcular las comunidades que hay en él. Hay varios algoritmos diseñados para la detección de comunidades, y en este caso utilizaremos el método de Lovaina. Los algoritmos de detección de comunidades se encuentran en el subpaquete community de networkx. Concretamente, nos centraremos en la funciónlouvain_communities() .

He aquí cómo utilizarlo:

communities = nx.community.louvain_communities(G)
print(communities)

[{'Jack', 'Claire', 'Anna', 'Steve'}, {'Bob', 'John', 'Jane'}, {'Rute', 'Alex'}]

El resultado es una lista de conjuntos, en la que cada conjunto representa una comunidad. Observamos que el algoritmo ha detectado tres comunidades, lo que coincide con nuestras expectativas dada la estructura del grafo.

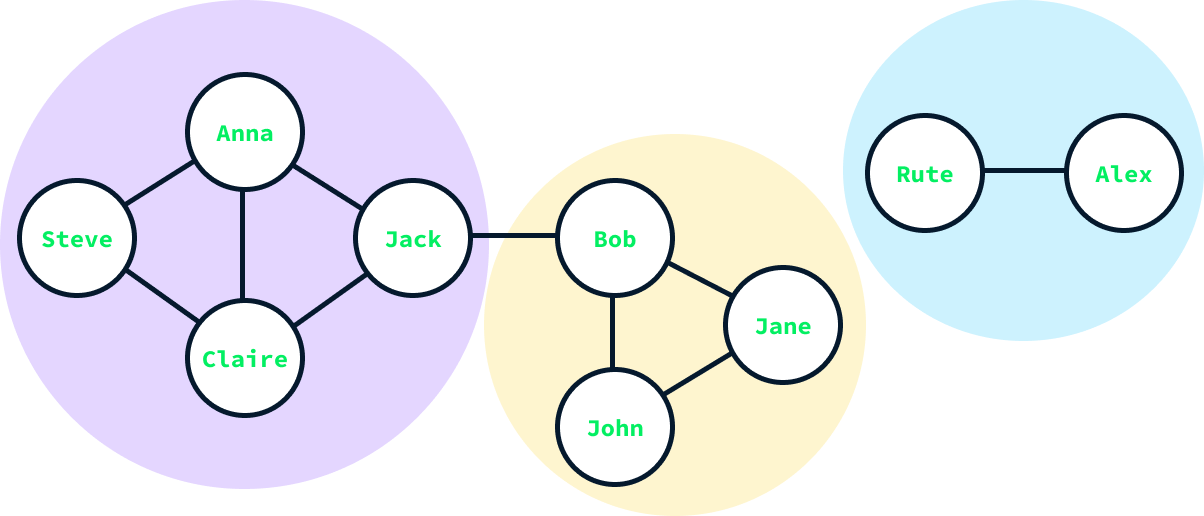
Para saber más sobre grafos, aprende a aplicar el algoritmo de Dijkstra en Python.

Elegir la estructura de datos adecuada

Al introducir cada estructura de datos, presentamos una lista de operaciones admitidas. Estas operaciones sirven de guía para saber cuándo utilizar esa estructura de datos, ya que está diseñada para realizar estas operaciones con eficacia.

Por ejemplo, Python list() también admite operaciones adicionales, como eliminar elementos. Sin embargo, estas operaciones adicionales no son en lo que destaca una lista de matrices. En concreto, eliminar un elemento de la mitad de una lista requiere copiar todos los datos (excepto el elemento eliminado) en una lista nueva, lo que puede llevar mucho tiempo.

Cuando los datos se indexan de forma natural con números, y se conoce el número de entradas (por ejemplo, los días de un mes), una matriz suele ser la opción preferida. Para una indexación más genérica o conjuntos de datos dinámicos, los diccionarios son una buena solución alternativa.

Para procesar los datos secuencialmente, una entrada cada vez, se suelen utilizar colas o pilas, según el orden deseado de procesamiento de los datos.

Los árboles suelen ser la respuesta cuando queremos realizar consultas más complejas sobre los datos, como encontrar todas las entradas dentro de un rango determinado o los extremos.

Por último, cuando existe una relación entre pares de puntos de datos, un gráfico es una forma eficaz de almacenar y representar estas relaciones. Existen algoritmos de grafos que nos permiten responder a preguntas habituales sobre conjuntos de datos con este tipo de relación por pares.

Las estructuras de datos constituyen un vasto dominio, y sólo hemos cubierto la punta del iceberg. En determinadas situaciones, la solución es diseñar una estructura de datos totalmente nueva y adaptada al problema en cuestión. No obstante, estar familiarizado con las estructuras de datos tratadas en este artículo debería orientarte en la dirección correcta a la hora de resolver tus problemas relacionados con los datos.

Conclusión

En este artículo, hemos aprendido que las estructuras de datos son métodos de organización de datos en formatos particulares para facilitar una recuperación eficaz de la información.

Hay dos tipos fundamentales de estructuras de datos: las basadas en matrices (por ejemplo, las tablas hash) y las basadas en nodos (por ejemplo, los grafos).

Las estructuras lineales, como las matrices, las colas y las pilas, organizan los elementos secuencialmente, uno tras otro. Por el contrario, las estructuras no lineales, como las tablas hash, los árboles y los grafos, organizan los datos basándose en las relaciones existentes entre ellos.

La elección de la estructura de datos adecuada depende de la naturaleza de las consultas que se vayan a realizar.

Si quieres aprender sobre las distintas estructuras de datos en Python, consulta este tutorial sobre estructuras de datos en Python.