Estruturas de dados: Um guia abrangente com exemplos em Python

As estruturas de dados existem tanto no mundo digital quanto no físico. Um dicionário é um exemplo físico de uma estrutura de dados em que os dados incluem definições de palavras organizadas em ordem alfabética em um livro. Essa organização permite uma consulta específica: dada uma palavra, você pode procurar sua definição.

Em sua essência, uma estrutura de dados é um método de organização de dados que facilita tipos específicos de consultas e operações sobre esses dados.

Começaremos abordando estruturas de dados lineares, como matrizes, listas, filas e pilhas. Em seguida, voltaremos a explicar a diferença entre estruturas lineares e não lineares antes de mergulharmos em tabelas hash, árvores e gráficos.

Se você quiser saber mais, confira este curso sobre estruturas de dados e algoritmos em Python.

Matrizes

As matrizes são estruturas de dados fundamentais amplamente disponíveis nas linguagens de programação. Eles permitem o armazenamento de um número fixo (N) de valores sequencialmente na memória.

Os elementos da matriz são indexados a partir do primeiro elemento no índice (0) até o último elemento no índice (N-1).

Eles permitem as seguintes operações:

1. Leia o valor em um determinado índice.
2. Atualiza o valor em um determinado índice.
3. Iterar sobre todos os valores armazenados.
4. Obter o tamanho da matriz.

As matrizes são altamente eficazes em cenários em que o número de valores a serem armazenados é conhecido antecipadamente e as operações principais envolvem a leitura e a gravação de dados em índices específicos.

Considere um cenário no qual você precisa armazenar leituras diárias de temperatura para o mês de dezembro. Talvez você queira permitir que os usuários recuperem a temperatura de um dia específico e realizem várias análises estatísticas sobre as temperaturas ao longo do mês.

Como o número de dias em dezembro é conhecido antecipadamente como 31, as matrizes são uma excelente opção para armazenar as leituras de temperatura. Inicialmente, você criaria uma matriz com 31 posições vazias. Então, depois de obter cada leitura de temperatura, a temperatura de um determinado dia seria atribuída ao índice de matriz correspondente: o dia 1 seria armazenado no índice 0, o dia 2 no índice 1 e assim por diante, até o dia 31, que seria armazenado no índice 30.

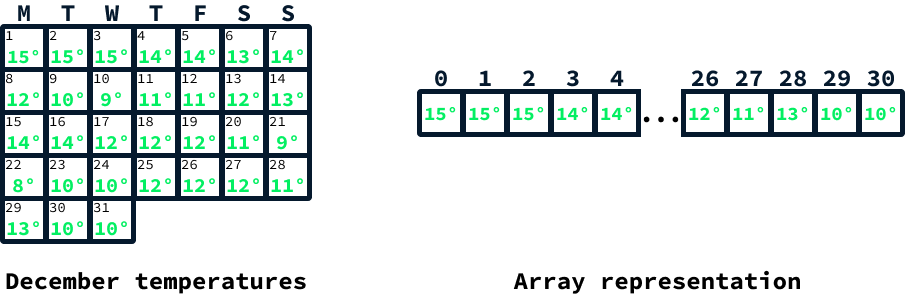
O acesso ao índice correspondente permite a recuperação da temperatura de um dia específico. Estatísticas, como a temperatura média, podem ser determinadas por meio da iteração de todos os elementos, mantendo uma soma cumulativa e, em seguida, dividindo-a pelo tamanho da matriz.

As matrizes não estão disponíveis nativamente no Python. Eles são usados nos bastidores como a estrutura subjacente de vários tipos de dados, mas não são diretamente compatíveis com a linguagem. Para usar matrizes explicitamente, você pode utilizar bibliotecas como a array, que oferece uma implementação de matriz. No entanto, muitas vezes é mais prático usar uma lista com um tamanho fixo em situações em que uma matriz pode ser necessária. As listas oferecem flexibilidade e são uma parte essencial da funcionalidade do Python, como discutiremos a seguir.

Podemos criar uma lista para simular uma matriz de 31 elementos, cada um inicializado como None, usando [None] * 31. Aqui, None indica que ainda não foi registrada nenhuma leitura de temperatura.

december_temperatures = [None] * 31

Para definir o valor em um índice específico, usamos december_temperatures[index], em que index é um número de 0 a 30. Por exemplo, para registrar a temperatura do primeiro dia (armazenada no índice 0), faríamos o seguinte:

december_temperatures[0] = 15

O acesso a uma temperatura é igualmente simples, usando december_temperatures[index].

print(december_temperatures[0])

15

Listas

Imagine agora que, em vez de nos concentrarmos em dezembro, instalamos um sensor em algum lugar para fazer leituras periódicas de temperatura durante um período não especificado. Nesse cenário, o uso de uma matriz não é a melhor opção, pois podemos ficar sem espaço devido ao seu tamanho fixo na criação.

Uma estrutura de dados mais adequada nesse cenário seria uma lista. Há dois tipos de listas:

• Listas de matrizes
• Listas vinculadas

Listas de matrizes

As listas de matrizes podem ser vistas como uma versão mais flexível das matrizes. Eles podem executar todas as funções que os arrays executam, mas também acrescentam novos valores, de modo que seu tamanho não é fixo na criação. As listas de matrizes correspondem ao uso de list() em Python.

Sua implementação se baseia no uso de uma matriz que é expandida quando o espaço se esgota, daí o nome array list. No entanto, como aprendemos anteriormente, as matrizes não podem crescer, então como isso é possível?

Quando a matriz subjacente de uma lista de matrizes está cheia e você deseja acrescentar um novo valor, uma matriz maior é criada sob o capô. Todos os valores anteriores são copiados para essa nova matriz maior. Em seguida, o novo valor é adicionado à primeira posição disponível na nova matriz.

Imagine que você queira acrescentar o valor 71 a essa matriz:

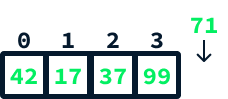
Isso pode ser feito da seguinte forma:

A quantidade de espaço novo alocado sempre que realizamos essa operação é crucial para o desempenho da lista de matrizes. Se, a cada append, criássemos uma matriz com apenas uma nova posição para o novo valor que está sendo anexado, isso significaria que cada operação de append exigiria a cópia de todos os dados pré-existentes. Isso seria extremamente ineficiente - imagine ter que copiar milhões de registros simplesmente para adicionar um novo.

Em vez disso, a estratégia comum é dobrar o tamanho do array sempre que for necessário mais espaço. Pode-se demonstrar que essa abordagem anula o efeito de ter essas etapas extras de cópia ao longo do tempo.

Para adicionar elementos a uma lista Python, usamos o método .append(). Aqui está um exemplo de como criar uma lista vazia e adicionar uma leitura de temperatura a ela:

temperatures = []
temperatures.append(35)

Listas vinculadas

Para estruturar os dados em um computador, precisamos de uma maneira de relacionar os valores entre si. Os arrays conseguem isso alocando locais de memória contíguos - ou seja, locais de memória diretamente próximos uns dos outros - e armazenando valores sequencialmente. Pense nisso como uma fileira de casas em uma rua: cada casa tem um endereço exclusivo (índice) e elas estão fisicamente localizadas uma ao lado da outra.

No entanto, esse não é o único método de organização de dados. Uma alternativa envolve o uso de uma estrutura baseada em nós.

Um nó é um objeto que armazena um valor junto com referências a outros nós. Por exemplo, para criar uma estrutura semelhante a uma lista usando nós, podemos ter um nó que contém um valor e uma referência ao próximo elemento da lista. Em Python, isso pode ser implementado com uma classe:

class Node:
    def __init__(self, value, next_node):
        self.value = value
        self.next_node = next_node

Usando essa abordagem, você pode criar uma lista vinculando valores por meio da referência next_node. Aqui está um trecho de código que cria uma lista com os valores 42, 17 e 37:

node_37 = Node(37, None) # There's no node after 37 so next_node is None
node_17 = Node(17, node_37)
node_42 = Node(42, node_17)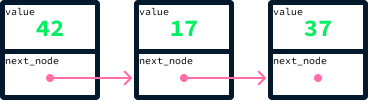

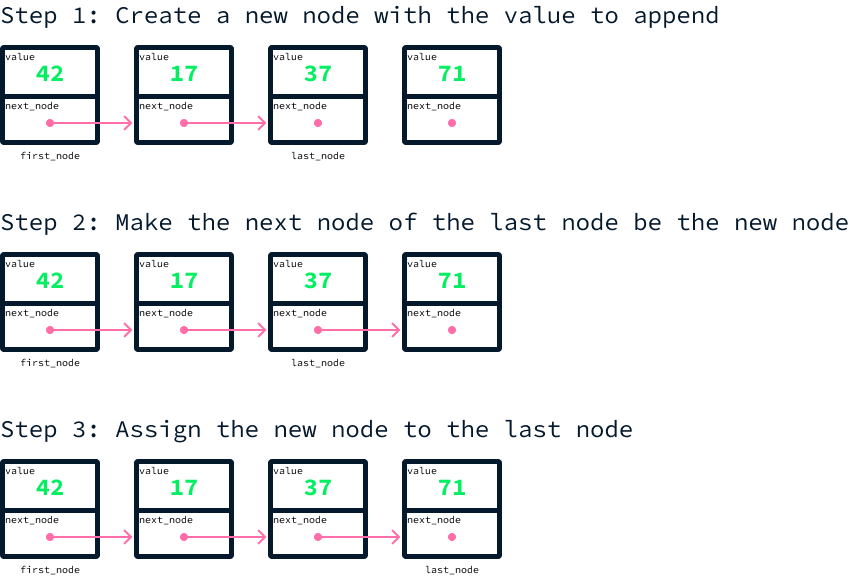
Não é prático vincular manualmente os nós dessa maneira. A implementação real requer a criação de outra classe que mantenha referências ao primeiro e ao último nós da lista. Para acrescentar um novo valor, você deve:

1. Crie um nó com o valor desejado.
2. Defina esse novo nó como o próximo nó do último nó atual.
3. Atualiza a referência do último nó para esse nó recém-adicionado.

Imagine que você queira acrescentar o valor 71 à nossa matriz de exemplo:

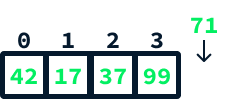
Isso pode ser feito da seguinte forma:

class LinkedList:
    def __init__(self):
        self.first_node = None
        self.last_node = None

    def append(self, value):
        node = Node(value, None)
        if self.first_node is None:
            self.first_node = node
            self.last_node = node
        else:
            self.last_node.next_node = node
            self.last_node = node

Ao contrário das listas de matriz, não podemos acessar diretamente os valores por seus índices. Para ler um valor específico em um índice, devemos começar no primeiro nó e passar sequencialmente de um nó para o outro até chegarmos ao índice desejado. Esse processo é significativamente mais lento do que o acesso direto. Se tivermos milhões de valores armazenados na lista, precisaremos ler milhões de valores na memória para chegar a um índice específico.

A vantagem de uma lista vinculada está no fato de que podemos adicionar e remover instantaneamente elementos da frente ou de trás da lista. Esse recurso abre a possibilidade de implementar duas novas estruturas de dados: filas e pilhas, que discutiremos a seguir.

Filas

Imagine que você está desenvolvendo um aplicativo de restaurante que registra os pedidos dos clientes e os encaminha para a cozinha. Quando os clientes chegam ao restaurante, eles fazem fila para fazer seus pedidos, esperando ser atendidos na sequência de sua chegada. Isso significa que o primeiro cliente da fila deve receber seu pedido primeiro, e o último cliente da fila deve receber seu pedido por último.

Na cozinha, o chef prefere se concentrar em um pedido de cada vez, portanto, o aplicativo deve exibir apenas o pedido atual. Depois que um pedido é preparado e despachado, o próximo pedido na fila deve ser exibido.

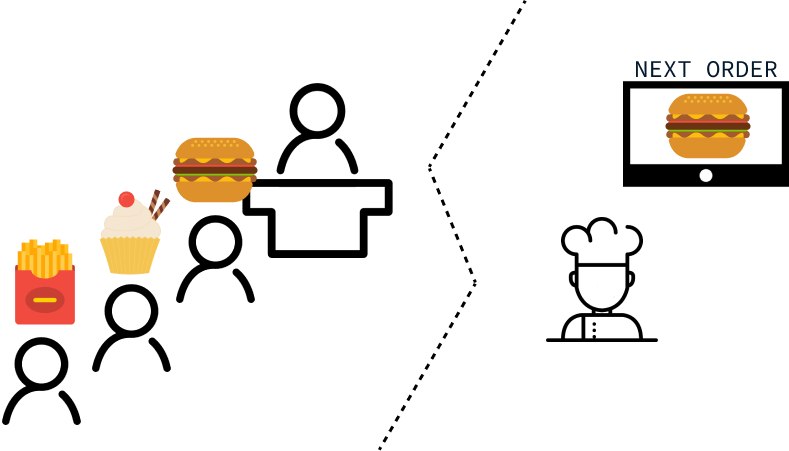
Podemos interpretar os requisitos acima como a necessidade de uma estrutura de dados que suporte as seguintes operações:

1. Adicionando elementos.
2. Exibindo o elemento que foi adicionado primeiro.
3. Removendo o elemento que foi adicionado primeiro.

Essas operações são exatamente o que uma fila oferece. Uma fila pode ser implementada usando uma lista vinculada, na qual os elementos são adicionados acrescentando-os à lista. Como os elementos são ordenados pelo tempo de chegada, o primeiro nó é sempre aquele que deve ser servido em seguida.

Veja como os pedidos acima seriam armazenados na fila:

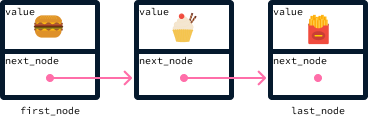
Quando um pedido estiver pronto, ele poderá ser removido atualizando o primeiro elemento para next_node, supondo que haja um nó subsequente. O novo primeiro nó se torna o segundo nó:

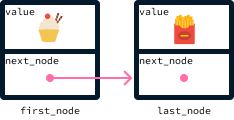
As filas são descritas como uma estrutura de dados FIFO ( first-in, first-out ) porque o primeiro elemento a ser adicionado também é o primeiro a ser removido. Em nosso exemplo de restaurante, o primeiro cliente a chegar também é o primeiro a ser servido (e removido da lista do chef).

Para usar uma fila no Python, podemos utilizar a coleçãodeque do módulo collections. Importe esse módulo e crie uma fila vazia, conforme mostrado abaixo:

from collections import deque
orders = deque()

Você pode adicionar um novo elemento ao final da fila usando o método.append():

orders.append("burger")
orders.append("sunday")
orders.append("fries")

Para recuperar e remover o próximo pedido do início da fila, usamos o método.popleft():

orders.append("burger")
orders.append("sunday")
orders.append("fries")

burger
sunday
fries

Pilhas

Em determinadas situações, desejamos o oposto do comportamento de uma fila - preferimos rastrear o elemento adicionado mais recentemente.

Para exemplificar isso, imagine que você tenha a tarefa de adicionar um recurso de desfazer a um editor de imagens. Isso requer um método para monitorar as ações do usuário, fornecendo acesso às operações mais recentes. Isso ocorre porque as funcionalidades de desfazer normalmente revertem as ações, começando pela última realizada e indo em direção à primeira.

Uma pilha é exatamente uma estrutura de dados que suporta essas operações:

1. Adicionando elementos.
2. Exibindo o elemento que foi adicionado pela última vez.
3. Removendo o elemento que foi adicionado por último.

Assim como as filas, as pilhas também podem ser implementadas usando uma lista vinculada. A adição de um elemento ainda é feita acrescentando-o à lista. No entanto, nosso interesse se volta para o último elemento da lista em vez do primeiro. Para recuperar o elemento mais recente, procuramos o último elemento da lista. A remoção do último elemento exige que você exclua o último elemento.

Em nossa estrutura de nós, apenas programamos o próximo nó. Para facilitar a remoção do último elemento, precisamos acessar o elemento que o precede, excluir seu next_node e promover esse nó para ser o último. Você pode fazer isso modificando a estrutura do nó para rastrear também o nó anterior de cada nó. Essa lista vinculada é chamada de lista duplamente vinculada.

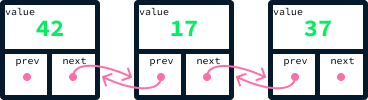
As pilhas são descritas como uma estrutura de dados do tipo último a entrar, primeiro a sair (LIFO), pois o último elemento a ser adicionado também é o primeiro a ser removido.

Para usar uma pilha em Python, podemos utilizar a mesma coleçãodeque . Usamos o método.append() para adicionar novos elementos:

from collections import deque
actions = deque()

actions.append("crop")
actions.append("desaturate")
actions.append("resize")

Para recuperar e remover o próximo pedido do topo da pilha, usamos o método.pop():

print(actions.pop())
print(actions.pop())
print(actions.pop())

resize
desaturate
crop

Linear vs. Estruturas de dados não lineares

Até agora, exploramos cinco estruturas de dados: matrizes, listas de matrizes, listas vinculadas, filas e pilhas. Cada uma delas é uma estrutura de dados linear, pois seus elementos são organizados em uma sequência, com cada elemento tendo um elemento anterior e um próximo claramente definidos.

Em seguida, mudaremos nosso foco para estruturas de dados não lineares. Diferentemente dos tipos lineares, essas estruturas não organizam os elementos um ao lado do outro de forma linear. Consequentemente, eles não têm uma noção definida de elementos anteriores e seguintes. Em vez disso, eles estabelecem diferentes tipos de relacionamentos entre os elementos.

Essa característica os torna particularmente adequados para a execução de consultas especializadas nos dados com alta eficiência, em vez de servir apenas como um meio de armazenar dados na memória.

Tabelas de hash

Começamos este artigo discutindo um exemplo real de uma estrutura de dados: dicionários. Acontece que organizar os dados de forma que possam ser pesquisados por um campo específico (por exemplo, pesquisar uma definição de uma palavra) é extremamente útil em geral, por isso os cientistas da computação também inventaram uma estrutura de dados que permite isso.

Para entender essa estrutura de dados, vamos ver como podemos criar um dicionário virtual, ou seja, uma estrutura de dados em que você pode:

1. Adicione uma palavra em sua definição.
2. Dada uma palavra, procure sua definição.

Lembre-se do exemplo do registro de temperaturas durante o mês de dezembro. Usamos uma matriz com 31 elementos correspondentes a cada dia do mês para armazenar as temperaturas em seus respectivos índices. Essa abordagem permite a busca eficiente da temperatura para um determinado dia.

Esse cenário é semelhante a lidar com pares de dados (day, temperature), em que o objetivo é recuperar o temperature especificando o dia. Da mesma forma, no caso dos dicionários, lidamos com pares de dados (word, definition) e procuramos encontrar o definition quando você recebe um word.

Esses pares são chamados de pares de valores-chave ou entradas. A chave é o parâmetro usado na consulta de pesquisa, e o valor é o resultado dessa consulta.

O que nos impede de usar uma matriz para o problema do dicionário é que nossas chaves são strings em vez de números. Com chaves numéricas, podemos usar diretamente uma matriz para associar chaves e valores, posicionando os valores em seus índices correspondentes.

Para resolver esse problema, primeiro precisamos converter as palavras em números. Uma função que realiza essa conversão é chamada de função hash. Há várias abordagens para criar essa função. Por exemplo, poderíamos atribuir valores numéricos às letras, com a como 1, b como 2, c como 3, e assim por diante, e depois somar esses valores.

Por exemplo, a palavra data seria calculada como 4 + 1 + 20 + 1 = 26. No entanto, essa função tem suas desvantagens, que discutiremos em breve. Os detalhes sobre como criar uma função hash eficaz estão além do objetivo deste artigo, mas o Python fornece convenientemente uma função hash() que lida eficientemente com essa tarefa para nós.

hash("data")

-6138587229816301269

No exemplo acima, você deve ter observado que a função hash produziu um número negativo. É importante observar que os índices positivos da matriz variam de 0 a N - 1. Depois de convertermos as chaves em números, podemos mapeá-las para o intervalo de 0 a N - 1 usando o operador de módulo % (que produz o restante de uma divisão - por exemplo, 10 % 3 produz 1).

Como observação, a função hash() do Python pode retornar valores diferentes em diferentes execuções do programa. Ele só é determinístico na mesma execução do programa, o que significa que você poderá observar valores de hash diferentes para o mesmo objeto se executar o programa várias vezes.

Considere uma matriz que contém 100 elementos. Para localizar o índice correspondente à string "data", você deve proceder da seguinte forma:

hash("data") % 100

31

A estrutura de dados da tabela de hash é essencialmente uma grande matriz que armazena pares de valores-chave em índices determinados pela aplicação de uma função de hash às chaves.

Devido a restrições de espaço, o diagrama acima inclui apenas a abreviação "def" para representar a definição. Entretanto, na prática, o segundo elemento de cada entrada seria a definição completa da palavra.

Há outro aspecto importante a ser considerado. Como há muito mais de 100 palavras, se continuarmos adicionando palavras, palavras distintas inevitavelmente produzirão o mesmo valor de hash. Para resolver isso, em vez de limitar cada elemento da matriz a um único par de valores-chave, empregamos uma lista vinculada para armazenar todas as entradas que compartilham o mesmo valor de hash.

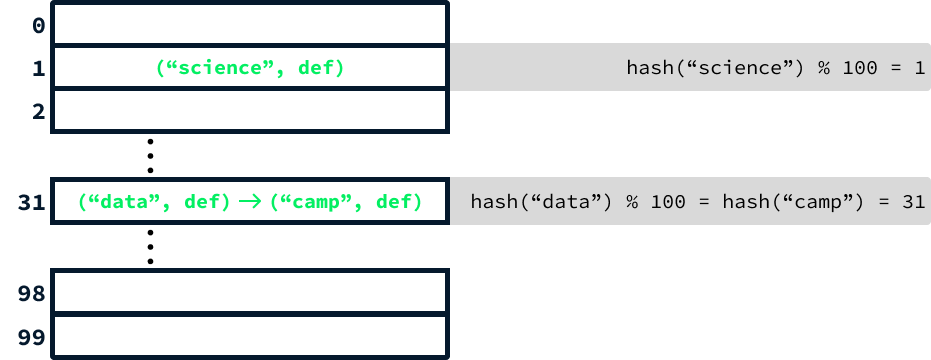
Quando duas entradas geram o mesmo hash, isso é chamado de colisão. Esse cenário modifica ligeiramente o processo de pesquisa. Depois de calcular o código hash, é necessário percorrer a lista para localizar a entrada correta. Embora essa abordagem torne a operação de pesquisa mais lenta, é possível demonstrar que o uso de um tamanho de matriz inicial suficientemente grande (maior que 100) e uma função hash bem projetada pode reduzir significativamente o impacto das colisões. Consequentemente, a eficiência permanece quase equivalente à de uma matriz.

Para uma função de hash projetada com eficiência, encontrar valores distintos que resultem no mesmo hash deve ser raro. É por isso que uma função de hash simplista que simplesmente soma os valores numéricos dos caracteres em uma palavra não é ideal. Quaisquer duas palavras compostas pelas mesmas letras, independentemente de sua ordem, produziriam códigos hash idênticos. Por exemplo, "listen" e "silent" produziriam o mesmo hash. Em contrapartida, a função hash integrada fornecida pelo Python é significativamente mais robusta e foi projetada especificamente para minimizar as colisões.

As tabelas Hash são, sem dúvida, a estrutura de dados mais importante disponível. Eles são extremamente eficientes e versáteis. Em Python, eles são implementados por meio da classe dict(). Devido à sua semelhança com um dicionário, em Python, a estrutura de dados é chamada de dicionário em vez de tabela de hash.

Para simplificar, nosso exemplo se concentra em adicionar e procurar entradas. Em geral, os dicionários oferecem mais flexibilidade e suportam operações adicionais, inclusive a exclusão. Para criar um dicionário vazio (tabela de hash) em Python, você pode usar {} desta forma:

word_definitions = {}
word_definitions["data"] = "Facts or information."

Você pode acessar a definição de uma palavra usando a palavra como chave, assim:

print(word_definitions["data"])

Facts or information.

Árvores

Imagine que você está desenvolvendo um site para uma agência imobiliária. Sua tarefa é criar um recurso que permita aos usuários filtrar as listagens por preço. O recurso deve permitir que os usuários:

1. Encontre a listagem mais barata.
2. Encontre a listagem mais cara.
3. Encontre todas as listagens abaixo de um determinado preço.

Normalmente, esse processo envolveria a análise de todos os anúncios de imóveis e a filtragem daqueles que estão fora da faixa de preço desejada. No entanto, nosso objetivo é desenvolver uma solução que seja dimensionada de forma mais eficiente, que não exija o exame de todo o conjunto de dados para encontrar listagens relevantes. As árvores são a estrutura de dados perfeita para responder a esse tipo de consulta.

As árvores são estruturas de dados baseadas em nós, como listas vinculadas. No entanto, em vez de ter referências anteriores e seguintes, cada nó manterá um valor e duas referências: um nó esquerdo e um nó direito.

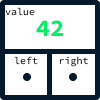
Em nosso exemplo de site de agência imobiliária, cada nó representará uma listagem de imóveis. Para otimizar as consultas relacionadas a preços, estabeleceremos uma regra: as listagens com preços mais baixos sempre serão armazenadas à esquerda de um nó, enquanto as listagens com preços mais altos sempre serão armazenadas à direita.

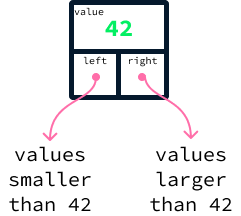
Para um exemplo concreto, considere a seguinte árvore que contém os valores 42, 17, 73, 4, 22 e 89.

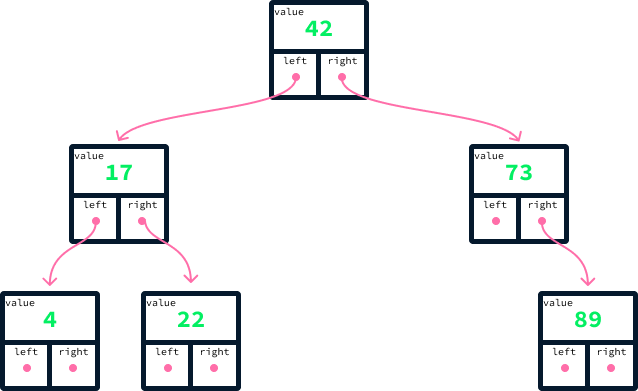
Para cada nó, todos os nós à esquerda têm valores menores, e todos os nós à direita têm valores maiores. Uma árvore que satisfaz essa propriedade é chamada de árvore de pesquisa binária (BST). Ele é binário porque cada nó se refere a no máximo dois outros nós, chamados de filhos. A parte de pesquisa do termo vem do fato de que a propriedade de ordenação nos filhos da esquerda e da direita possibilitará a pesquisa eficiente na árvore.

Já podemos ver como um BST ajuda a encontrar rapidamente as listagens mais baratas e mais caras. Devido à ordenação de valores, o nó mais barato é sempre o mais à esquerda e o mais caro é sempre o mais à direita.

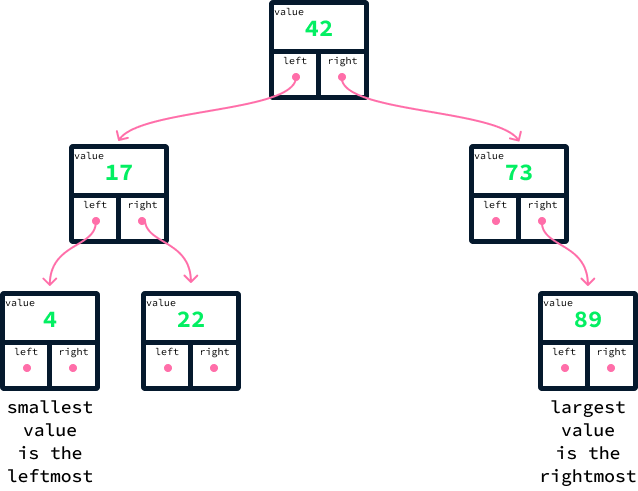
Isso significa que podemos localizá-los sem examinar a maioria dos dados. Começando pelo nó superior, também chamado de nó raiz, seguimos consistentemente os links à esquerda para identificar o mínimo e os links à direita para identificar o máximo. Isso significa que somente os nós ao longo do caminho que conecta a raiz aos nós mínimo e máximo, respectivamente, precisam ser inspecionados.

Imagine que você queira encontrar todos os nós com um valor de pelo menos 50. Estas são as etapas que você pode seguir para conseguir isso:

• Começando pela raiz, comparamos nosso alvo, 50, com o valor da raiz, que é 42.
• Observando que 50 é maior, entendemos que a raiz e todos os nós à sua esquerda contêm valores menores. Consequentemente, podemos desconsiderá-los.
• Em seguida, passamos para o nó à direita da raiz, que é 73. Após a comparação, descobrimos que 50 é menor do que 73. Isso indica que todos os nós à direita do nó 73 atendem aos nossos critérios.
• No entanto, como 73 não tem um filho esquerdo, nossa busca termina aí.

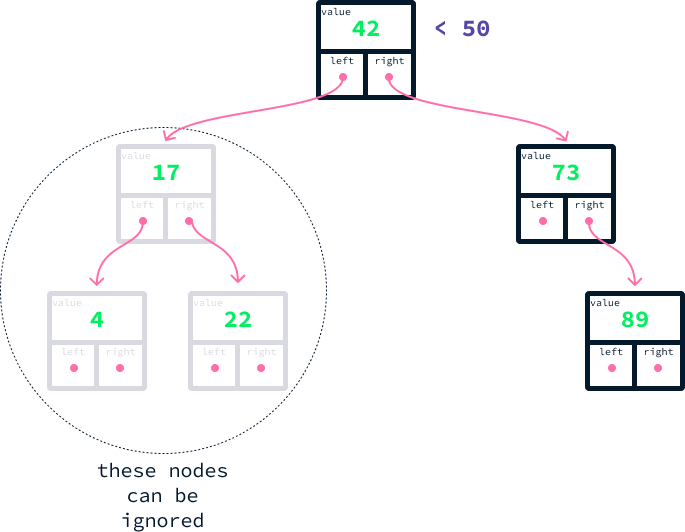
Já podemos ver como os BSTs podem acelerar significativamente as consultas. Mesmo nesse pequeno exemplo, evitamos examinar metade dos dados.

Em geral, a identificação de todos os nós em um BST que se encaixam em um determinado intervalo exige a inspeção de vários nós que estão próximos do número de resultados da consulta. Essa é uma grande vantagem em comparação com a necessidade de inspecionar cada ponto de dados. Imagine que você tenha 1.000.000 de listagens e uma consulta que produza apenas 10 resultados. Usando uma lista, você teria que inspecionar um milhão de listagens para filtrar aquelas que não se encaixam no intervalo. Com um BST, você só precisa inspecionar cerca de 10 listagens. Isso representa um fator de aumento de velocidade de 100.000.

A eficiência de um BST depende muito do equilíbrio da árvore. Se adicionarmos os mesmos valores de antes, do menor para o maior - 4, 17, 22, 42, 73, seguido de 89 -, poderemos ter uma árvore desequilibrada, conforme mostrado:

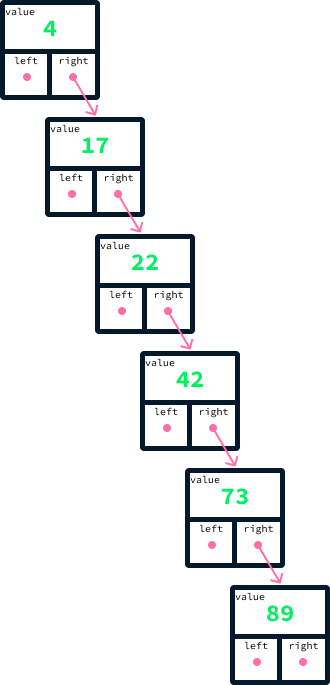
Lembre-se de que, para encontrar o valor máximo em um BST, começamos na raiz e rastreamos os links à direita até chegarmos a um nó que não tenha um. No caso de uma árvore desequilibrada, como a ilustrada no diagrama acima, esse processo exige o exame de cada nó. O ideal é que os nós sejam distribuídos uniformemente entre os lados esquerdo e direito. Explicar os detalhes de como esse equilíbrio pode ser alcançado de forma consistente está fora do escopo deste artigo. Um tipo de árvore de pesquisa binária conhecida por manter esse equilíbrio é chamada de árvore AVL.

O pacote avltree fornece uma implementação de uma árvore AVL. O trecho de código abaixo mostra como podemos usá-lo nesse conjunto de dados de listagem de casas, um subconjunto limpo desse conjunto de dados de imóveis dos EUA.

import csv
from avltree import AvlTree as Tree

# Load the listings CSV data
with open("listings.csv", "rt") as f:
    reader = csv.reader(f)
    listings = list(reader)

# Create the tree based on the price column (column index 2)
tree = Tree()
for listing in listings[1:]:
    price = float(listing[2])
    tree[price] = listing

# Display the cheapest listing price
print("Cheapest:", tree.minimum())

# Display the most expensive listing price
print("Most expensive:", tree.maximum())

# Display the number of listings whose price is between 100,000 and 110,000
listings_in_range = list(tree.between(100000, 110000))
print("Num listings between 100000 and 110000:", len(listings_in_range))

Cheapest: 50017.0
Most expensive: 19999900.0
Num listings between 100000 and 110000: 403

Primeiro, usamos o módulocsv para ler o conjunto de dados listings.csv. Em seguida, criamos uma árvore AVL com base na coluna de preço. Em seguida, usamos os métodos minimum(), maximum() e between() para determinar o preço mínimo, o preço máximo e o número de listagens com preços entre US$ 100.000 e US$ 110.000.

Gráficos

A última estrutura de dados que discutiremos neste artigo é o gráfico.

Digamos que você esteja analisando dados de uma plataforma de mídia social. Esses dados incluem uma lista de usuários e as amizades entre eles, e seu objetivo é identificar comunidades dentro da rede social. Embora o conceito de comunidade possa ser definido de várias maneiras, ele geralmente se refere a um grupo de usuários que têm um número significativo de amizades dentro desse grupo.

Os gráficos são a estrutura de dados ideal para representar dados quando temos entidades e relacionamentos entre pares dessas entidades. Em nosso exemplo, as entidades são usuários e os relacionamentos são suas amizades.

Os gráficos são estruturas baseadas em nós. No entanto, diferentemente das listas vinculadas e das árvores, que exibem conexões lineares ou hierárquicas entre os nós, um gráfico permite que qualquer nó se conecte a vários outros nós. Essas conexões entre os nós, chamadas de bordas, indicam relacionamentos entre eles.

Em nosso exemplo de rede social, cada usuário pode ser visualizado como um nó. Uma borda pode ser desenhada entre dois nós para indicar uma amizade entre os usuários correspondentes.

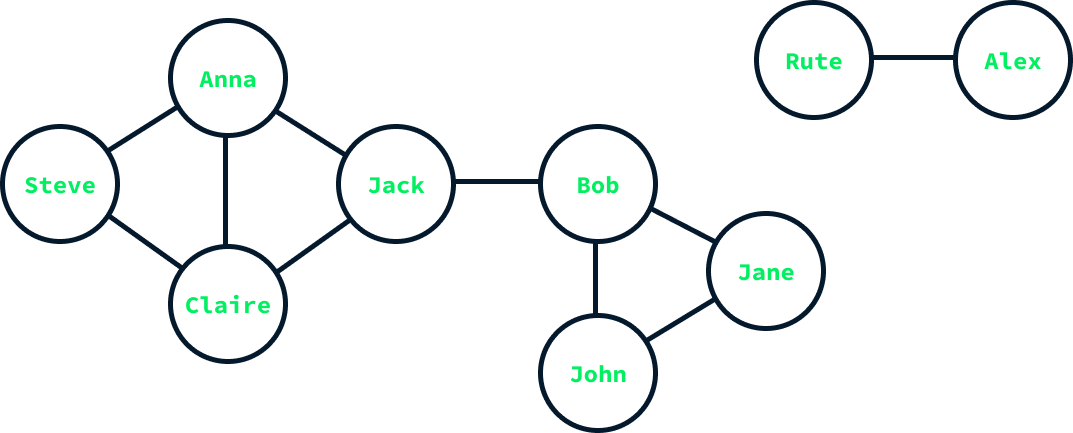
O diagrama acima ilustra um gráfico que representa amizades em uma pequena rede social. Os nós representam os usuários e são identificados com seus nomes, enquanto as bordas representam as amizades. Por exemplo, Anna é amiga de Steve, Claire e Jack, o que significa que há arestas conectando seu nó aos nós desses indivíduos.

As operações que uma estrutura de dados de gráfico deve suportar incluem:

1. Adicionando um novo nó.
2. Conectando dois nós com uma borda.
3. Recuperação de todos os nós conectados a um nó específico.

Uma maneira comum de implementar um gráfico é usar uma tabela de hash e listas. Uma tabela de hash é criada com uma entrada para cada nó. A chave de cada entrada é o nó, e o valor é uma lista que contém todos os nós aos quais esse nó está conectado.

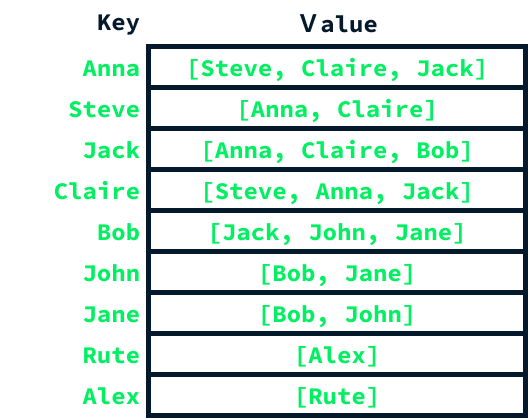
O pacotenetworkx oferece a você uma implementação Python para criar e manipular gráficos. Além disso, a biblioteca networkx abrange uma grande variedade de algoritmos de gráficos, inclusive os de detecção de comunidades. Vamos utilizá-lo para construir o gráfico mencionado anteriormente e aplicar um algoritmo de detecção de comunidade predominante para observar os resultados.

Para iniciar a criação do gráfico, começamos importando a biblioteca networkx e inicializando um gráfico vazio:

import networkx as nx
G = nx.Graph()

Os nós podem ser adicionados usando o métodoadd_node() .

G.add_node("Anna")
G.add_node("Steve")
G.add_node("Jack")
G.add_node("Claire")
G.add_node("Bob")
G.add_node("Jane")
G.add_node("John")
G.add_node("Rute")
G.add_node("Alex")

As bordas podem ser adicionadas usando o métodoadd_edge() .

G.add_edge("Anna", "Steve")
G.add_edge("Anna", "Jack")
G.add_edge("Anna", "Claire")
G.add_edge("Steve", "Claire")
G.add_edge("Claire", "Jack")
G.add_edge("Jack", "Bob")
G.add_edge("Bob", "John")
G.add_edge("Bob", "Jane")
G.add_edge("John", "Jane")
G.add_edge("Rute", "Alex")

Com nosso gráfico criado, podemos calcular as comunidades dentro dele. Vários algoritmos foram desenvolvidos para a detecção de comunidades e, neste caso, usaremos o método Louvain. Os algoritmos de detecção de comunidade podem ser encontrados no subpacote community de networkx. Especificamente, vamos nos concentrar na funçãolouvain_communities() .

Veja como você pode utilizá-lo:

communities = nx.community.louvain_communities(G)
print(communities)

[{'Jack', 'Claire', 'Anna', 'Steve'}, {'Bob', 'John', 'Jane'}, {'Rute', 'Alex'}]

O resultado é uma lista de conjuntos, com cada conjunto representando uma comunidade. Observamos que o algoritmo detectou três comunidades, o que corresponde às nossas expectativas, dada a estrutura do gráfico.

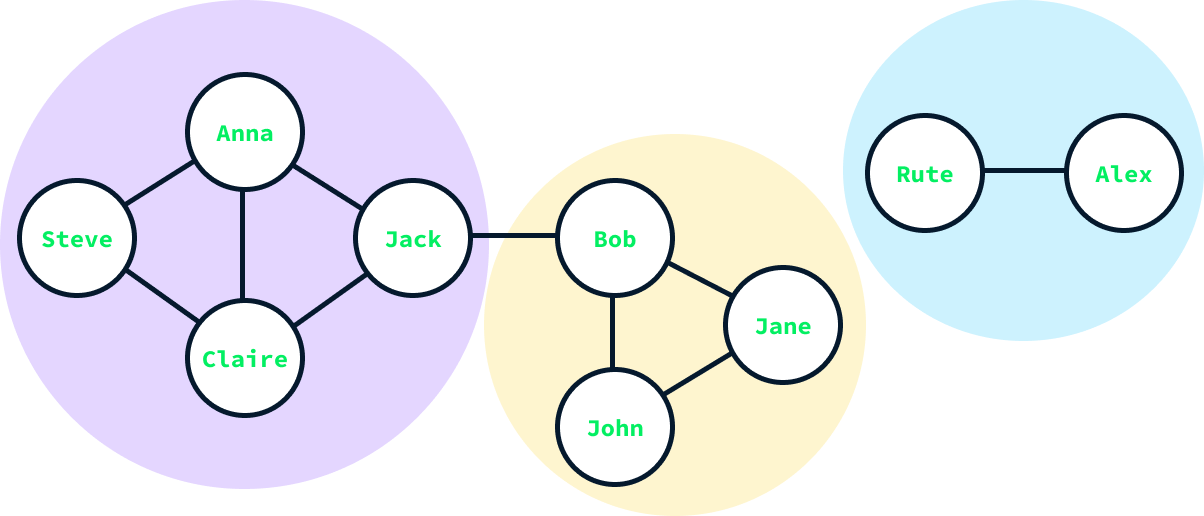
Para saber mais sobre gráficos, saiba como implementar o algoritmo Dijkstra em Python.

Escolhendo a estrutura de dados correta

Ao introduzir cada estrutura de dados, apresentamos uma lista de operações suportadas. Essas operações servem como diretrizes para quando você deve usar essa estrutura de dados, pois ela foi projetada para realizar essas operações de forma eficiente.

Por exemplo, o Python list() também oferece suporte a operações adicionais, como a remoção de elementos. No entanto, não é nessas operações extras que uma lista de matriz se destaca. Especificamente, a remoção de um elemento do meio de uma lista requer a cópia de todos os dados (exceto o elemento removido) em uma nova lista, o que pode consumir muito tempo.

Quando os dados são naturalmente indexados com números e o número de entradas é conhecido (por exemplo, os dias de um mês), uma matriz geralmente é a opção preferida. Para indexação mais genérica ou conjuntos de dados dinâmicos, os dicionários são uma boa solução alternativa.

Para processar dados sequencialmente, uma entrada de cada vez, filas ou pilhas são usadas com frequência, dependendo da ordem desejada para o processamento de dados.

Normalmente, as árvores são a resposta quando queremos realizar consultas mais complexas nos dados, como encontrar todas as entradas dentro de um determinado intervalo ou extremos.

Por fim, quando há uma relação entre pares de pontos de dados, um gráfico é uma forma eficaz de armazenar e representar essas relações. Existem algoritmos de gráficos que nos permitem responder a perguntas comuns sobre conjuntos de dados com esse tipo de relação de pares.

As estruturas de dados constituem um vasto domínio, e cobrimos apenas a ponta do iceberg. Em determinadas situações, a solução é projetar uma nova estrutura de dados totalmente adaptada ao problema em questão. No entanto, estar familiarizado com as estruturas de dados discutidas neste artigo deve indicar a direção certa para você resolver seus problemas relacionados a dados.

Conclusão

Neste artigo, aprendemos que as estruturas de dados são métodos de organização de dados em formatos específicos para facilitar a recuperação eficiente de informações.

Há dois tipos fundamentais de estruturas de dados: estruturas baseadas em matrizes (por exemplo, tabelas de hash) e estruturas baseadas em nós (por exemplo, gráficos).

Estruturas lineares, como matrizes, filas e pilhas, organizam os elementos sequencialmente, um após o outro. Por outro lado, as estruturas não lineares, como tabelas de hash, árvores e gráficos, organizam os dados com base nas relações dentro dos dados.

A escolha da estrutura de dados adequada depende da natureza das consultas a serem realizadas.

Se você quiser saber mais sobre as várias estruturas de dados em Python, confira este tutorial sobre estruturas de dados em Python.