Implementación del Algoritmo de Dijkstra en Python: Un tutorial paso a paso

¿Por qué aprender el Algoritmo de Dijkstra?

El de Dijkstra es el algoritmo de referencia para encontrar el camino más corto entre dos puntos de una red, que tiene muchas aplicaciones. Es fundamental en informática y teoría de grafos. Comprenderlo y aprender a aplicarlo abre las puertas a algoritmos y aplicaciones de grafos más avanzados.

También enseña un valioso enfoque de resolución de problemas mediante su algoritmo codicioso, que consiste en hacer la elección óptima en cada paso basándose en la información actual.

Esta habilidad es transferible a otros algoritmos de optimización. Puede que el algoritmo de Dijkstra no sea el más eficiente en todos los escenarios, pero puede ser una buena referencia para resolver problemas de "distancia más corta".

Algunos ejemplos son:

• Los sistemas de navegación GPS encuentran la ruta más rápida
• Enrutamiento de paquetes de datos en redes informáticas
• Los servicios de reparto optimizan las rutas para ser más eficientes
• Redes sociales (sugerir conexiones)
• Finanzas (encontrar vías óptimas de inversión)
• Gestión de proyectos (encontrar el flujo de trabajo más eficaz)

Aunque no te interese ninguna de estas cosas, implementar el algoritmo de Dijkstra en Python te permitirá practicar conceptos importantes como:

• Clases de Python
• Comprensiones de diccionario
• Comprensiones de listas
• Colas prioritarias

Conceptos clave relacionados con los gráficos

Para aplicar el algoritmo de Dijkstra en Python, necesitamos refrescar algunos conceptos esenciales de la teoría de grafos. En primer lugar, tenemos los propios gráficos:

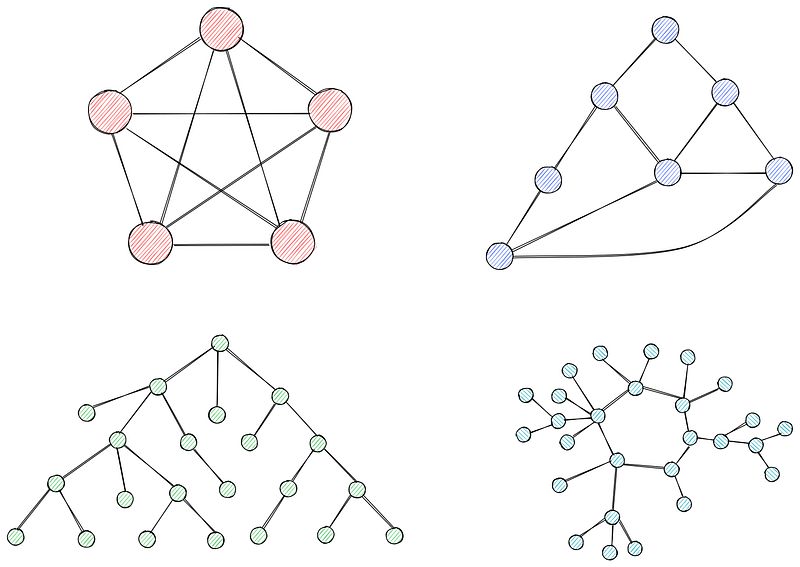
Los grafos son conjuntos de nodos (vértices ) conectados por aristas. Los nodos representan entidades o puntos de una red, mientras que las aristas representan la conexión o relaciones entre ellos.

Los gráficos pueden ser ponderados o no ponderados. En los grafos no ponderados, todas las aristas tienen el mismo peso (a menudo fijado en 1). En los grafos ponderados (lo has adivinado), cada arista tiene asociado un peso, que suele representar el coste, la distancia o el tiempo.

En el tutorial utilizaremos grafos ponderados, ya que son necesarios para el algoritmo de Dijkstra.

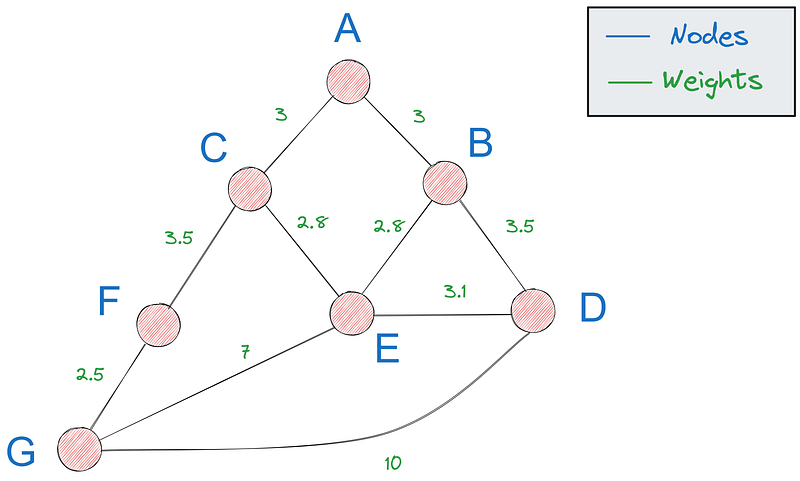
Una trayectoria en un grafo se refiere a una secuencia de nodos conectados por aristas, que empiezan y terminan en nodos específicos. El camino más corto, que es el que nos interesa en este tutorial, es el camino con el mínimo peso total (distancia, coste, etc.).

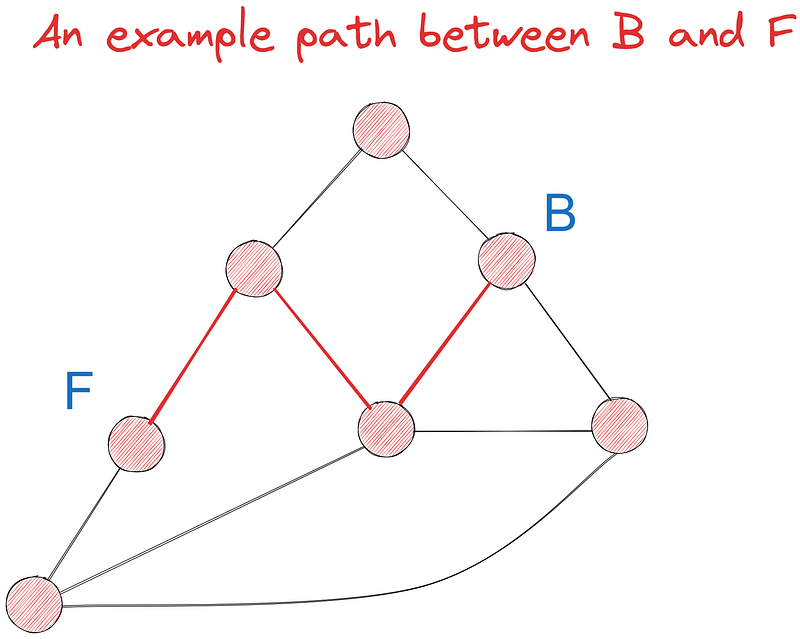
El algoritmo de Dijkstra explicado visualmente

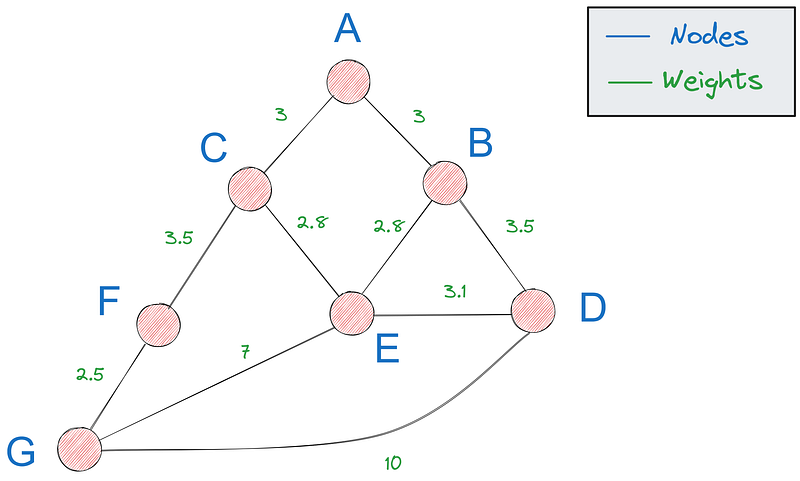
Para el resto del tutorial, utilizaremos el último gráfico que vimos:

Intentemos encontrar el camino más corto entre los puntos B y F utilizando el algoritmo de Dijkstra entre al menos siete caminos posibles. Inicialmente, realizaremos la tarea visualmente y la implementaremos en código más adelante.

En primer lugar, inicializamos el algoritmo del siguiente modo:

1. Establecemos B como nodo raíz (origen).
2. Fijamos las distancias entre B y todos los demás nodos en infinito como sus valores de distancia iniciales y provisionales. Fijamos el valor de B en 0, ya que es la distancia a sí mismo:

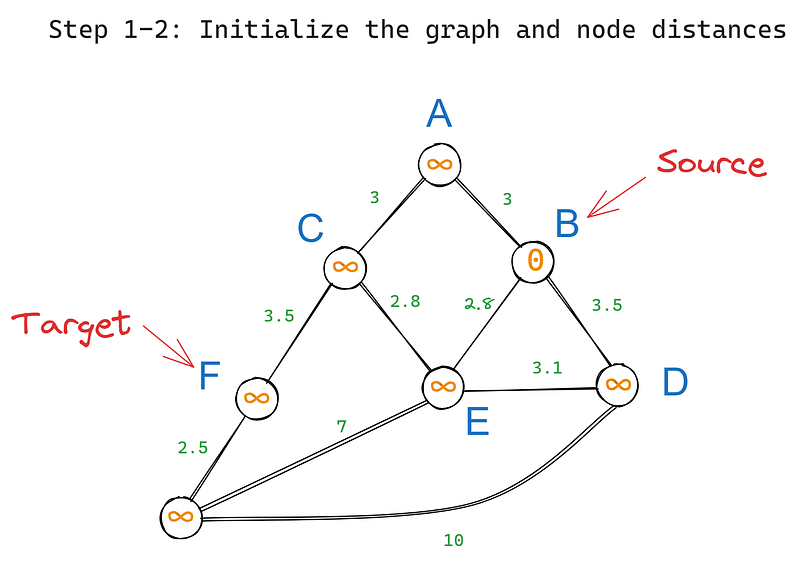
A continuación, ejecutamos los siguientes pasos de forma iterativa:

1. Elige el nodo con el valor más pequeño como "nodo actual" y visita todos sus nodos vecinos. A medida que visitamos a cada vecino, actualizamos sus valores tentativos desde el infinito hasta sus pesos de arista empezando por el nodo origen.
2. Una vez visitados todos los vecinos del nodo actual, marcamos el nodo actual como "visitado". Una vez que un nodo está marcado como "visitado", su valor ya es el camino más corto desde el objetivo.
3. El algoritmo vuelve al paso 1 y elige el nodo con el valor más pequeño.

En nuestro grafo, B tiene tres vecinos: A, D y E. Visitemos cada uno de ellos empezando por el nodo raíz y actualicemos sus valores (iteración 1) en función de los pesos de sus aristas:

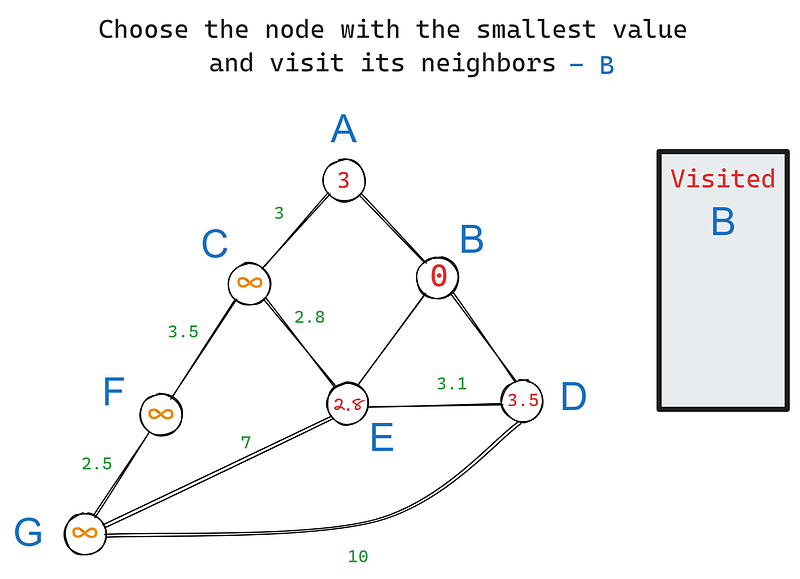
En la iteración 2, volvemos a elegir el nodo con el valor más pequeño, esta vez E. Sus vecinos son C, D y G. B queda excluido porque ya lo hemos visitado. Actualicemos los valores de los vecinos de E:

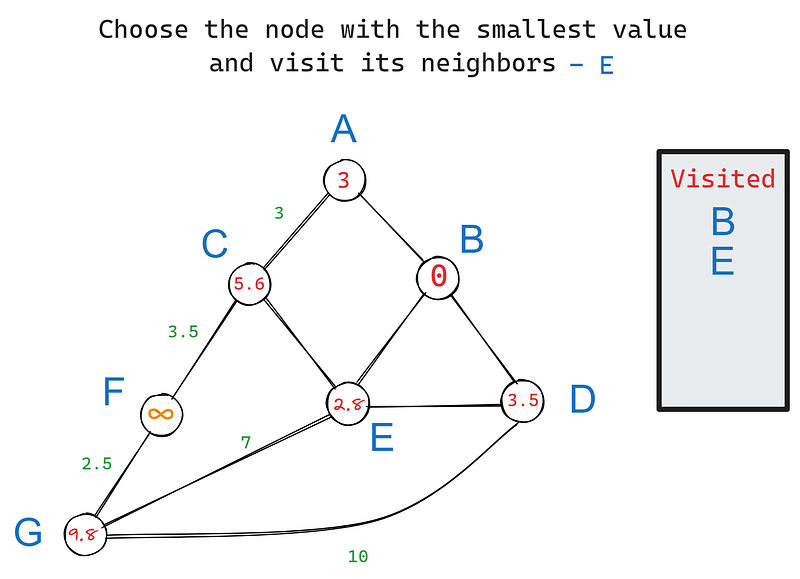
Fijamos el valor de C en 5,6 porque su valor es la suma acumulada de los pesos de B a C. Lo mismo ocurre con G. Sin embargo, si te fijas, el valor de D sigue siendo 3,5 cuando debería haber sido 3,5 + 2,8 = 6,3, al igual que con los demás nodos.

La regla es que si la nueva suma acumulada es mayor que el valor actual del nodo, no lo actualizaremos porque el nodo ya indica la distancia más corta a la raíz. En este caso, el valor actual de D, 3,5, ya señala la distancia más corta a B, porque son vecinos.

Continuamos de este modo hasta visitar todos los nodos. Cuando eso ocurra finalmente, tendremos la distancia más corta a cada nodo desde B y podremos buscar simplemente el valor de B a F.

En resumen, los pasos son:

1. Inicializa el grafo con el nodo origen que tomará el valor 0 y todos los demás nodos infinito. Empieza con el origen como "nodo actual".
2. Visita todos los nodos vecinos del nodo actual y actualiza sus valores a la suma acumulada de pesos (distancias) desde el origen. Si el valor actual de un vecino es menor que la suma acumulada, permanece igual. Marca el "nodo actual" como finalizado.
3. Marca el nodo de valor mínimo inacabado como "nodo actual".
4. Repite los pasos 2 y 3 hasta terminar con todos los nodos.

Implementación paso a paso del Algoritmo de Dijkstra en Python

Ahora, para consolidar tu comprensión del algoritmo de Dijkstra, aprenderemos a implementarlo en Python paso a paso.

Entender los gráficos como diccionarios

En primer lugar, necesitamos una forma de representar grafos en Python: la opción más popular es utilizar un diccionario. Si este es nuestro gráfico

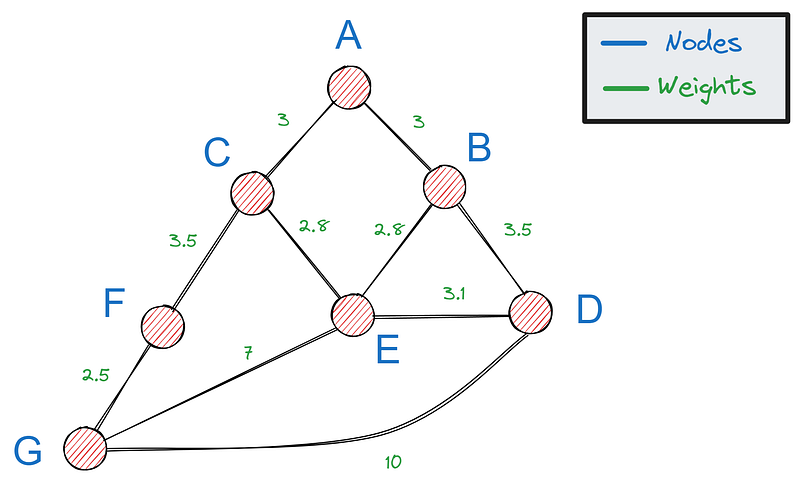
Podemos representarlo con el siguiente diccionario:

graph = {
   "A": {"B": 3, "C": 3},
   "B": {"A": 3, "D": 3.5, "E": 2.8},
   "C": {"A": 3, "E": 2.8, "F": 3.5},
   "D": {"B": 3.5, "E": 3.1, "G": 10},
   "E": {"B": 2.8, "C": 2.8, "D": 3.1, "G": 7},
   "F": {"G": 2.5, "C": 3.5},
   "G": {"F": 2.5, "E": 7, "D": 10},
}

Cada clave del diccionario es un nodo y cada valor es un diccionario que contiene los vecinos de la clave y las distancias a ella. Nuestro grafo tiene siete nodos, lo que significa que el diccionario debe tener siete claves.

Otras fuentes suelen referirse al diccionario anterior como una lista de adyacencia de diccionario. A partir de ahora también nos ceñiremos a ese término.

1. Crear una Graph clase

Para que nuestro código sea más modular y fácil de seguir, implementaremos una sencilla clase Graph para representar gráficos. En realidad, utilizará una lista de adyacencia de diccionario. También tendrá un método para añadir fácilmente conexiones entre dos nodos:

class Graph:
   def __init__(self, graph: dict = {}):
       self.graph = graph  # A dictionary for the adjacency list

   def add_edge(self, node1, node2, weight):
       if node1 not in self.graph:  # Check if the node is already added
           self.graph[node1] = {}  # If not, create the node
       self.graph[node1][node2] = weight  # Else, add a connection to its neighbor

Utilizando esta clase, podemos construir nuestro grafo iterativamente desde cero, de la siguiente manera

G = Graph()

# Add A and its neighbors
G.add_edge("A", "B", 3)
G.add_edge("A", "C", 3)

# Add B and its neighbors
G.add_edge("B", "A", 3)
G.add_edge("B", "D", 3.5)
G.add_edge("B", "E", 2.8)

...

O podemos pasar directamente una lista de adyacencia de diccionario, que es un método más rápido:

# Use the dictionary we defined earlier
G = Graph(graph=graph)

G.graph

{'A': {'B': 3, 'C': 3},
'B': {'A': 3, 'D': 3.5, 'E': 2.8},
'C': {'A': 3, 'E': 2.8, 'F': 3.5},
'D': {'B': 3.5, 'E': 3.1, 'G': 10},
'E': {'B': 2.8, 'C': 2.8, 'D': 3.1, 'G': 7},
'F': {'G': 2.5, 'C': 3.5},
'G': {'F': 2.5, 'E': 7, 'D': 10}}

2. Utilizar un diccionario para almacenar las distancias desde el origen

Creamos otro método de clase, esta vez para el propio algoritmo:shortest_distances:

class Graph:
   def __init__(self, graph: dict = {}):
       self.graph = graph

   # The add_edge method omitted for space

   def shortest_distances(self, source: str):
       # Initialize the values of all nodes with infinity
       distances = {node: float("inf") for node in self.graph}
       distances[source] = 0  # Set the source value to 0

       ...

Lo primero que hacemos dentro del método es definir un diccionario que contenga pares nodo-valor. Este diccionario se actualiza cada vez que visitamos un nodo y sus vecinos. Como hemos mencionado en la explicación visual del algoritmo, los valores iniciales de todos los nodos se fijan en infinito, mientras que el valor de la fuente es 0.

Cuando terminemos de escribir el método, se devolverá este diccionario, que tendrá las distancias más cortas a todos los nodos desde el origen. Podremos hallar así la distancia de B a F:

# Sneak-peek - find the shortest paths from B
distances = G.shortest_distances("B")

to_F = distances["F"]
print(f"The shortest distance from B to F is {to_F}")

3. Utilizar una cola de prioridad para iterar sobre los nodos

Ahora necesitamos una forma de hacer un bucle sobre los nodos del grafo basándonos en las reglas del algoritmo de Dijkstra. Si recuerdas, en cada iteración tenemos que elegir el nodo con el valor más pequeño y visitar a sus vecinos.

Podrías decir que basta con hacer un bucle sobre las claves del diccionario:

for node in graph.keys():
   ...

Este método no funciona, ya que no nos ofrece ninguna forma de ordenar los nodos en función de su valor. Por tanto, las matrices simples no serán suficientes. Para resolver esta parte del problema, utilizaremos algo llamado cola prioritaria.

Una cola de prioridad es como una lista normal (array), pero cada uno de sus elementos tiene un valor extra para representar su prioridad. Este es un ejemplo de cola prioritaria:

pq = [(3, "A"), (1, "C"), (7, "D")]

Esta cola contiene tres elementos -A, C y D- y cada uno de ellos tiene un valor de prioridad que determina cómo se realizan las operaciones sobre la cola. Python proporciona una biblioteca heapq integrada para trabajar con colas de prioridad:

from heapq import heapify, heappop, heappush

La biblioteca tiene tres funciones que nos interesan:

• heapify: Convierte una lista de tuplas con pares prioridad-valor en una cola de prioridad.
• heappush: Añade un elemento a la cola con su prioridad asociada.
• heappop: Elimina y devuelve el elemento de mayor prioridad (el de menor valor).

pq = [(3, "A"), (1, "C"), (7, "D")]

# Convert into a queue object
heapify(pq)

# Return the highest priority value
heappop(pq)

(1, 'C')

Como puedes ver, después de convertir pq en una cola utilizando heapify, pudimos extraer C en función de su prioridad. Intentemos empujar un valor:

heappush(pq, (0, "B"))

heappop(pq)

(0, 'B')

La cola se actualiza correctamente en función de la prioridad del nuevo elemento porque heappop devolvió el nuevo elemento con prioridad 0.

Ten en cuenta que después de hacer saltar un elemento, dejará de formar parte de la cola.

Ahora, volviendo a nuestro algoritmo, después de inicializar distances, creamos una nueva cola de prioridad que sólo contiene inicialmente el nodo origen:

class Graph:
   def __init__(self, graph: dict = {}):
       self.graph = graph

   def shortest_distances(self, source: str):
       # Initialize the values of all nodes with infinity
       distances = {node: float("inf") for node in self.graph}
       distances[source] = 0  # Set the source value to 0

       # Initialize a priority queue
       pq = [(0, source)]
       heapify(pq)

       # Create a set to hold visited nodes
       visited = set()

La prioridad de cada elemento dentro de pq será su valor actual. También inicializamos un conjunto vacío para registrar los nodos visitados.

4. El algoritmo de Dijkstra como while loop

Ahora, empezamos a iterar sobre todos los nodos no visitados utilizando un bucle while:

class Graph:
   def __init__(self, graph: dict = {}):
       self.graph = graph

   def shortest_distances(self, source: str):
       # Initialize the values of all nodes with infinity
       distances = {node: float("inf") for node in self.graph}
       distances[source] = 0  # Set the source value to 0

       # Initialize a priority queue
       pq = [(0, source)]
       heapify(pq)

       # Create a set to hold visited nodes
       visited = set()

       while pq:  # While the priority queue isn't empty
           current_distance, current_node = heappop(
               pq
           )  # Get the node with the min distance

           if current_node in visited:
               continue  # Skip already visited nodes
           visited.add(current_node)  # Else, add the node to visited set

Mientras la cola de prioridad no esté vacía, seguimos saltando el nodo de mayor prioridad (con el valor mínimo) y extrayendo su valor y nombre a current_distance y current_node. Si la current_node está dentro de visited, la omitimos. En caso contrario, lo marcamos como visitado y pasamos a visitar a sus vecinos:

while pq:  # While the priority queue isn't empty
   current_distance, current_node = heappop(pq)

   if current_node in visited:
       continue 
   visited.add(current_node)

   for neighbor, weight in self.graph[current_node].items():
       # Calculate the distance from current_node to the neighbor
       tentative_distance = current_distance + weight
       if tentative_distance < distances[neighbor]:
           distances[neighbor] = tentative_distance
           heappush(pq, (tentative_distance, neighbor))

return distances

Para cada vecino, calculamos la distancia provisional desde el nodo actual sumando el valor actual del vecino al peso de la arista de conexión. A continuación, comprobamos si la distancia es menor que la distancia del vecino en distances. En caso afirmativo, actualizamos el diccionario distances y añadimos el vecino con su distancia tentativa a la cola de prioridad.

Eso es. Hemos aplicado el algoritmo de Dijkstra. Vamos a probarlo:

G = Graph(graph)

distances = G.shortest_distances("B")
print(distances, "\n")

to_F = distances["F"]
print(f"The shortest distance from B to F is {to_F}")

{'A': 3, 'B': 0, 'C': 5.6, 'D': 3.5, 'E': 2.8, 'F': 9.1, 'G': 9.8}

The shortest distance from B to F is 9.1

Por tanto, la distancia de B a F es 9,1. Pero espera: ¿de qué camino se trata?

5. Construir el camino más corto

Por tanto, sólo tenemos las distancias más cortas, no los caminos, lo que hace que nuestro grafo tenga este aspecto:

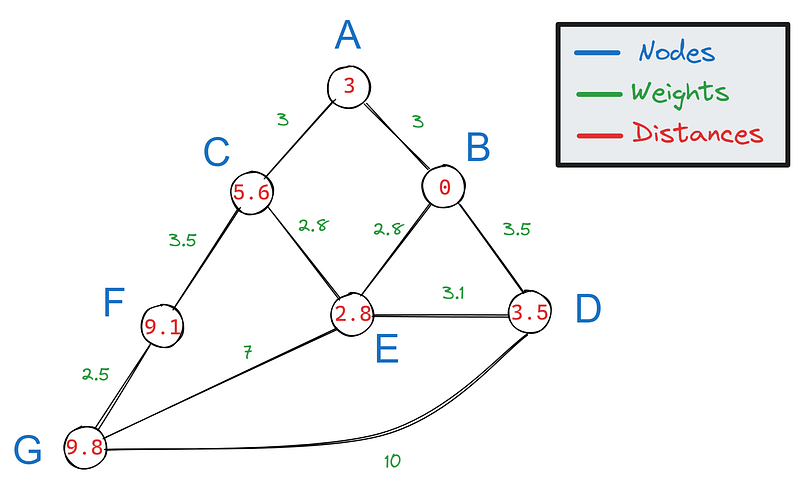
Para construir el camino más corto a partir de la distancia más corta calculada, podemos volver sobre nuestros pasos desde el objetivo. Por cada arista conectada a F, restamos su peso:

1. 9.1–3.5 = 5.6
2. 9.1–2.5 = 6.5

A continuación, vemos si alguno de los resultados coincide con el valor de los vecinos de F. Sólo 5,6 coincide con el valor de C, lo que significa que C forma parte del camino más corto.

Volvemos a repetir este proceso para los vecinos de C, A y E:

1. 5.6–3 = 2.6
2. 5.6–2.8 = 2.8

Como 2,8 coincide con el valor de E, forma parte del camino más corto. E también es vecino de B, por lo que el camino más corto entre B y F es BECF.

Añadamos la implementación de este proceso a nuestra clase. El código en sí es un poco diferente de la explicación anterior, porque encuentra los caminos más cortos entre B y todos los demás nodos, no sólo con F.

También lo hace a la inversa, pero la idea es la misma.

Añade las siguientes líneas de código al final del método shortest_distances eliminando la antigua declaración return:

predecessors = {node: None for node in self.graph}

for node, distance in distances.items():
   for neighbor, weight in self.graph[node].items():
       if distances[neighbor] == distance + weight:
           predecessors[neighbor] = node

return distances, predecessors

Cuando se ejecuta el código, el diccionario predecessors contiene el padre inmediato de cada nodo implicado en el camino más corto hacia el origen. Vamos a intentarlo:

G = Graph(graph)

distances, predecessors = G.shortest_distances("B")

print(predecessors)

{'A': 'B', 'B': None, 'C': 'E', 'D': 'B', 'E': 'B', 'F': 'C', 'G': 'E'}

En primer lugar, vamos a encontrar manualmente el camino más corto utilizando el diccionario predecessors retrocediendo desde F:

# Check the predecessor of F
predecessors["F"]

'C'  # It is C

# Check the predecessor of C
predecessors["C"]

'E'  # It is E

# Check the predecessor of E
predecessors["E"]

'B'  # It is B

Ya está. El diccionario nos dice correctamente que el camino más corto entre B y F es BECF.

Pero encontramos el método de forma semimanual. Queremos un método que devuelva automáticamente el camino más corto construido a partir del diccionario predecessors desde cualquier origen a cualquier destino. Definimos este método como shortest_path (añádelo al final de la clase):

def shortest_path(self, source: str, target: str):
   # Generate the predecessors dict
   _, predecessors = self.shortest_distances(source)

   path = []
   current_node = target

   # Backtrack from the target node using predecessors
   while current_node:
       path.append(current_node)
       current_node = predecessors[current_node]

   # Reverse the path and return it
   path.reverse()

   return path

Utilizando la función shortest_distances, generamos el diccionario predecessors. A continuación, iniciamos un bucle while que retrocede un nodo desde el nodo actual en cada iteración hasta alcanzar el nodo origen. A continuación, devolvemos la lista invertida, que contiene la ruta del origen al destino.

Vamos a probarlo:

G = Graph(graph)

G.shortest_path("B", "F")

['B', 'E', 'C', 'F']

¡Funciona! Probemos con otra:

G.shortest_path("A", "G")

['A', 'C', 'F', 'G']

Perfectamente.

Conclusión

En este tutorial hemos aprendido uno de los algoritmos más fundamentales de la teoría de grafos: el de Dijkstra. Suele ser el algoritmo más utilizado para encontrar el camino más corto entre dos puntos en estructuras gráficas. Debido a su sencillez, tiene aplicaciones en muchas industrias, como:

• Logística y transporte
• Redes y telecomunicaciones
• Fabricación y robótica
• Finanzas e inversión
• Urbanismo

Espero que la implementación del algoritmo de Dijkstra en Python haya despertado tu interés por el maravilloso mundo de los algoritmos de grafos. Si quieres saber más, te recomiendo encarecidamente los siguientes recursos:

• Curso de Introducción al Análisis de Redes en Python
• Curso de Estructuras de Datos y Algoritmos en Python