programa
La regularización de abandono es una técnica utilizada en redes neuronales para evitar el sobreajuste, que se produce cuando un modelo aprende el ruido de los datos de entrenamiento en lugar del patrón real.
En 2012, Geoffrey Hinton (galardonado con el Premio Turing) y sus colegas presentaron la técnica en un artículo de investigacióny desde entonces se ha adaptado ampliamente para entrenar modelos de aprendizaje profundo.
Este tutorial introducirá el concepto de regularización por abandono, reforzará por qué la necesitamos, e introducirá las funciones que ayudan a implementarla en PyTorch. También aprenderás detalles de implementación mediante ejemplos prácticos, con consejos avanzados para utilizar eficazmente el abandono en tus futuros proyectos de aprendizaje profundo.
¿Qué es la regularización del abandono escolar y por qué la necesitamos?
La idea central del abandono es "abandonar" aleatoriamente (poner a cero) una fracción de las neuronas de la red durante la fase de entrenamiento. Esto significa que un determinado porcentaje de neuronas se ignora o se "descarta" durante cada pasada hacia delante y hacia atrás, haciendo que la arquitectura de la red sea dinámicamente diferente en cada lote de entrenamiento.
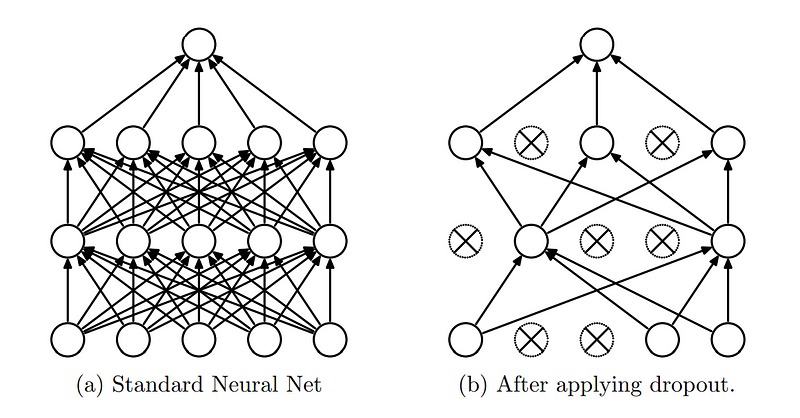
Regularización del abandono. (Fuente)
La capa de abandono se ha convertido en una capa esencial en las redes neuronales debido a las ventajas que proporciona:
- Evitar el sobreajuste: El abandono elimina aleatoriamente neuronas específicas durante el entrenamiento, evitando que la red dependa demasiado de ellas. En general, ésta es la prestación básica para la que utilizamos el abandono.
- Mejorar la generalización: Como en cada iteración de entrenamiento se descartan neuronas diferentes, la red entrena efectivamente múltiples subredes. Este comportamiento de conjunto mejora la capacidad de generalización del modelo.
- Reducir la coadaptación: Las neuronas de una red pueden coadaptarse, lo que significa que desarrollan dependencias entre sí. El abandono reduce estas dependencias asegurando que cada neurona funcione de forma más independiente, mejorando la capacidad de la red para aprender características valiosas.
Ya que entendemos el concepto de abandono, vamos a sumergirnos en su puesta en práctica.
Comprender la capa de abandono en PyTorch
Bibliotecas populares de aprendizaje profundo como Tensorflow y PyTorch han proporcionado módulos y funciones simplificados, por lo que implementar la regularización de abandono en modelos de redes neuronales es sencillo.
Como sugiere el título, este tutorial se centra en la implementación de la regularización de abandono utilizando PyTorch, pero si decides hacerlo en Tensorflow, las instrucciones están disponibles en la documentación oficial de Tensorflow.
PyTorch es una biblioteca de aprendizaje automático de código abierto desarrollada por el Laboratorio de Investigación de Inteligencia Artificial (FAIR) de Facebook (ahora Meta), que se utiliza ampliamente para aplicaciones de aprendizaje profundo e inteligencia artificial. En PyTorch, el abandono puede implementarse utilizando la función torch.nn.Dropout Class.
La clase antorcha.nn.Abandono
La sintaxis de la torch.nn.Dropout es la siguiente
torch.nn.Dropout(p=0.5, inplace=False)Dónde:
- p es la probabilidad de que un elemento sea cero. El valor por defecto es 0,5.
- inplace: si se establece en True, esta operación será in place. Por defecto es Falso.
En esta función, durante el entrenamiento, la capa de abandono pone a cero aleatoriamente algunos elementos del tensor de entrada con probabilidad p. Los elementos puestos a cero se eligen independientemente para cada llamada hacia delante y se muestrean a partir de una distribución Bernoulli. Cada canal se pone a cero independientemente en cada llamada de reenvío.
Durante la evaluación, la capa de abandono está desactivada, lo que significa que la capa calcula una función de identidad. Esto garantiza que todas las neuronas estén activas y que no se aplique ningún escalado.
Ya que hemos comprendido cómo funciona la regularización de abandonos y la función utilizada en PyTorch, vamos a ponerlo en común mediante un ejemplo práctico a continuación.
Ejemplo práctico: Construir un modelo de red neuronal con regularización de abandono
Tomaremos el popular conjunto de datos MNIST y construiremos una sencilla red neuronal convolucional para detectar números manuscritos a partir de imágenes. Luego aprenderemos a añadir capas de abandono a la red neuronal y examinaremos su impacto.
La configuración del entorno
En primer lugar, si no has instalado Python, puedes encontrar las instrucciones de instalación en el sitio web oficial de Python. Una vez instalado Python, puedes utilizar el gestor de paquetes pip para instalar las bibliotecas de PyTorch .
Abre tu terminal y ejecuta el siguiente comando:
pip install torch torchvisionTen en cuenta que las librerías PyTorch dependen de tu entorno y de la versión de CUDA. El sitio documentación oficial de instalación proporciona instrucciones claras de instalación basadas en la configuración de tu entorno.
Si tienes prisa por probar los códigos y prefieres saltarte la configuración del entorno, puedes abrir un nuevo cuaderno Google Collab con PyTorch preinstalado para ponerte manos a la obra inmediatamente.
El conjunto de datos MNIST
Desde el conjunto de datos MNIST (Instituto Nacional de Estándares y Tecnología Modificado) está disponible directamente en la biblioteca PyTorch, no tenemos que descargarlo de otro sitio.
El conjunto de datos MNIST es una gran colección de dígitos manuscritos que se utiliza habitualmente para entrenar y probar. Consta de 70.000 imágenes en escala de grises de dígitos (0-9), divididas en 60.000 imágenes de entrenamiento y 10.000 imágenes de prueba. Cada imagen está etiquetada con el dígito que representa, lo que la convierte en un conjunto de datos de aprendizaje supervisado.

El conjunto de datos MNIST.
Cargaremos las bibliotecas pertinentes y leeremos el conjunto de datos.
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
# Transformation to normalize the data
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
# Loading the MNIST dataset
full_dataset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = torchvision.datasets.MNIST(root='./data', train=False, download=True, transform=transform)
# Splitting the dataset into training and validation sets
train_size = int(0.8 * len(full_dataset))
val_size = len(full_dataset) - train_size
train_dataset, val_dataset = random_split(full_dataset, [train_size, val_size])
train_loader = DataLoader(dataset=train_dataset, batch_size=100, shuffle=True)
val_loader = DataLoader(dataset=val_dataset, batch_size=100, shuffle=False)
test_loader = DataLoader(dataset=test_dataset, batch_size=100, shuffle=False)Para este ejemplo, el 20% de las imágenes de entrenamiento se han dividido en imágenes de validación. A continuación, comprobamos las dimensiones de los conjuntos de datos:
# Inspecting the train dataset
train_data_iter = iter(train_loader)
train_images, train_labels = next(train_data_iter)
print(f"Train Images Shape: {train_images.shape}")
print(f"Train Labels Shape: {train_labels.shape}")
print("-----------------------------------------")
# Inspecting the val dataset
val_data_iter = iter(val_loader)
val_images, val_labels = next(val_data_iter)
print(f"Validation Images Shape: {val_images.shape}")
print(f"Validation Labels Shape: {val_labels.shape}")
print("-----------------------------------------")
# Inspecting the test dataset
test_data_iter = iter(test_loader)
test_images, test_labels = next(test_data_iter)
print(f"Test Images Shape: {test_images.shape}")
print(f"Test Labels Shape: {test_labels.shape}")
El resultado es el siguiente

Salida: Las dimensiones del conjunto de datos.
Estos resultados indican que los lotes contienen 100 imágenes, cada una con un canal y dimensiones de 28x28 píxeles. Las etiquetas son simplemente un tensor 1D de tamaño 100, que corresponde a las etiquetas de cada imagen del lote.
Definir el modelo sin abandono
Una vez cargados y transformados los datos, definimos un modelo de red neuronal convolucional simple, siendo el primero el modelo que no utiliza abandono.
# Define the CNN Without Dropout
class CNNWithoutDropout(nn.Module):
def __init__(self):
super(CNNWithoutDropout, self).__init__()
self.conv1 = nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2, padding=0)
self.fc1 = nn.Linear(64 * 7 * 7, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.pool(torch.relu(self.conv1(x)))
x = self.pool(torch.relu(self.conv2(x)))
x = x.view(-1, 64 * 7 * 7)
x = torch.relu(self.fc1(x))
x = self.fc2(x)
return x
model_without_dropout = CNNWithoutDropout()Tras la definición del modelo, definimos el optimizador y la función de pérdida.
criterion = nn.CrossEntropyLoss()
optimizer_without_dropout = optim.SGD(model_without_dropout.parameters(), lr=0.01, momentum=0.9)Entrenamiento del modelo base
A continuación, entrenamos el modelo sin abandono, registrando las métricas de entrenamiento y validación. Escribamos los códigos como funciones para poder reutilizarlos más adelante.
def train_validate_model(model, train_loader, val_loader, criterion, optimizer, num_epochs=10):
train_losses = []
val_losses = []
train_accuracies = []
val_accuracies = []
for epoch in range(num_epochs):
model.train()
running_loss = 0.0
correct = 0
total = 0
for images, labels in train_loader:
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
epoch_loss = running_loss / len(train_loader)
epoch_accuracy = 100 * correct / total
train_losses.append(epoch_loss)
train_accuracies.append(epoch_accuracy)
# Validation Phase
model.eval()
val_loss = 0.0
correct = 0
total = 0
with torch.no_grad():
for images, labels in val_loader:
outputs = model(images)
loss = criterion(outputs, labels)
val_loss += loss.item()
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
val_loss /= len(val_loader)
val_accuracy = 100 * correct / total
val_losses.append(val_loss)
val_accuracies.append(val_accuracy)
print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {epoch_loss:.4f}, Accuracy: {epoch_accuracy:.2f}%, Val Loss: {val_loss:.4f}, Val Accuracy: {val_accuracy:.2f}%')
return train_losses, val_losses, train_accuracies, val_accuraciesAhora podemos llamar a esta función con los conjuntos de datos de entrenamiento y validación.
train_losses_without_dropout, val_losses_without_dropout, train_accuracies_without_dropout, val_accuracies_without_dropout = train_validate_model(
model_without_dropout, train_loader, val_loader, criterion, optimizer_without_dropout
)
A continuación verás las métricas de entrenamiento y validación:

Salida: Métricas de entrenamiento y validación.
La precisión de validación es ligeramente inferior a la de entrenamiento. Incluso sin abandono, el modelo funciona excepcionalmente bien durante la fase de entrenamiento y validación, demostrando una gran precisión tanto en el conjunto de entrenamiento como en el de validación.
Evaluación del modelo de referencia
Una vez completado el entrenamiento, podemos evaluar cómo se comporta el modelo en las imágenes de prueba para obtener la puntuación de precisión de la prueba, que nos sirve como puntuación de referencia antes de añadir capas de abandono.
def evaluate_model(model, test_loader, criterion):
model.eval()
correct = 0
total = 0
with torch.no_grad():
for images, labels in test_loader:
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
accuracy = 100 * correct / total
return accuracy
accuracy_without_dropout = evaluate_model(model_without_dropout, test_loader, criterion)
print(f'Accuracy of the model without dropout on the test images: {accuracy_without_dropout:.2f}%')La precisión final resultante, como vemos, es:
![]()
Salida: Precisión en las imágenes de prueba.
El 99,07% de precisión es extremadamente bueno, ligeramente inferior a la precisión de entrenamiento pero mejor que la precisión de validación. Veamos cómo se comporta el modelo cuando añadimos capas de abandono, que dificultan el aprendizaje de los dígitos manuscritos.
Definición del modelo con abandono
Ahora sabemos cómo definir, entrenar y evaluar una red neuronal sencilla. Repitamos el procedimiento, partiendo de una definición de modelo y añadiendo una capa de abandono.
# Define the CNN With Dropout
class CNNWithDropout(nn.Module):
def __init__(self):
super(CNNWithDropout, self).__init__()
self.conv1 = nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2, padding=0)
self.dropout = nn.Dropout(p=0.5) # Dropout layer with 50% probability
self.fc1 = nn.Linear(64 * 7 * 7, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.pool(torch.relu(self.conv1(x)))
x = self.pool(torch.relu(self.conv2(x)))
x = x.view(-1, 64 * 7 * 7)
x = self.dropout(torch.relu(self.fc1(x))) # Apply dropout after ReLU activation
x = self.fc2(x)
return x
model_with_dropout = CNNWithDropout()Observa el cambio de código: Se han añadido dos nuevas líneas de código, que añaden las capas de abandono a la definición del modelo. Sí, añadir capas desplegables es tan sencillo como unas pocas líneas de código utilizando la función correspondiente disponible en PyTorch.
Mantenemos nuestra función de pérdida y el optimizador igual que en el modelo base.
criterion = nn.CrossEntropyLoss()
optimizer_with_dropout = optim.SGD(model_with_dropout.parameters(), lr=0.01, momentum=0.9)Entrenamiento del modelo con abandono
A continuación, entrenamos el modelo con abandono reutilizando las funciones escritas anteriormente y registrando las métricas de entrenamiento y validación.
train_losses_with_dropout, val_losses_with_dropout, train_accuracies_with_dropout, val_accuracies_with_dropout = train_validate_model(
model_with_dropout, train_loader, val_loader, criterion, optimizer_with_dropout
)
Las puntuaciones de entrenamiento y validación resultantes son:
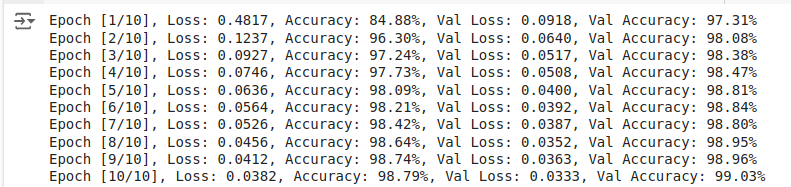
Salida: Métricas de entrenamiento y validación.
En comparación con el modelo con abandono, el modelo sin abandono consigue una mayor precisión de entrenamiento y una menor pérdida de entrenamiento, lo que es de esperar, ya que el abandono introduce ruido durante el entrenamiento, lo que dificulta que el modelo se ajuste perfectamente a los datos de entrenamiento.
A pesar de la reducción de las puntuaciones de entrenamiento, la precisión de validación del modelo con abandono ha aumentado.
Evaluación del modelo con abandono
Durante las fases de evaluación (incluida la validación), se desactivan las capas de abandono. Esto significa que todas las unidades están activas, y que no hay entradas caídas.
En PyTorch, el cambio entre los modos de entrenamiento y evaluación se realiza utilizando model.train() y model.eval()respectivamente:
model.train(): Establece el modelo en modo de entrenamiento, activando el abandono y otros comportamientos específicos del entrenamiento, como la normalización por lotes.model.eval(): Establece el modelo en modo de evaluación, desactivando el abandono y utilizando la red completa para las predicciones.
Calculemos la precisión de la prueba:
accuracy_with_dropout = evaluate_model(model_with_dropout, test_loader, criterion)
print(f'Accuracy of the model with dropout on the test images: {accuracy_with_dropout:.2f}%')La precisión resultante es la siguiente
![]()
Salida: Precisión en las imágenes de prueba.
Obtenemos una precisión del 99,12%, ligeramente mejor que la que obtuvimos con el modelo sin abandono.
Comparación del efecto del abandono en las redes neuronales
Ya que hemos almacenado todas las métricas durante nuestras fases de entrenamiento, validación y evaluación, vamos a representarlas en gráficos utilizando Matplotlib para analizarlas mejor.
El código para hacerlo es el siguiente
# Plotting the Results
plt.figure(figsize=(14, 10))
# Plot training loss
plt.subplot(2, 2, 1)
plt.plot(train_losses_without_dropout, label='Without Dropout')
plt.plot(train_losses_with_dropout, label='With Dropout')
plt.title('Training Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
# Plot validation loss
plt.subplot(2, 2, 2)
plt.plot(val_losses_without_dropout, label='Without Dropout')
plt.plot(val_losses_with_dropout, label='With Dropout')
plt.title('Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
# Plot training accuracy
plt.subplot(2, 2, 3)
plt.plot(train_accuracies_without_dropout, label='Without Dropout')
plt.plot(train_accuracies_with_dropout, label='With Dropout')
plt.title('Training Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy (%)')
plt.legend()
# Plot validation accuracy
plt.subplot(2, 2, 4)
plt.plot(val_accuracies_without_dropout, label='Without Dropout')
plt.plot(val_accuracies_with_dropout, label='With Dropout')
plt.title('Validation Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy (%)')
plt.legend()
plt.tight_layout()
plt.show()
Los gráficos de comparación son los siguientes:
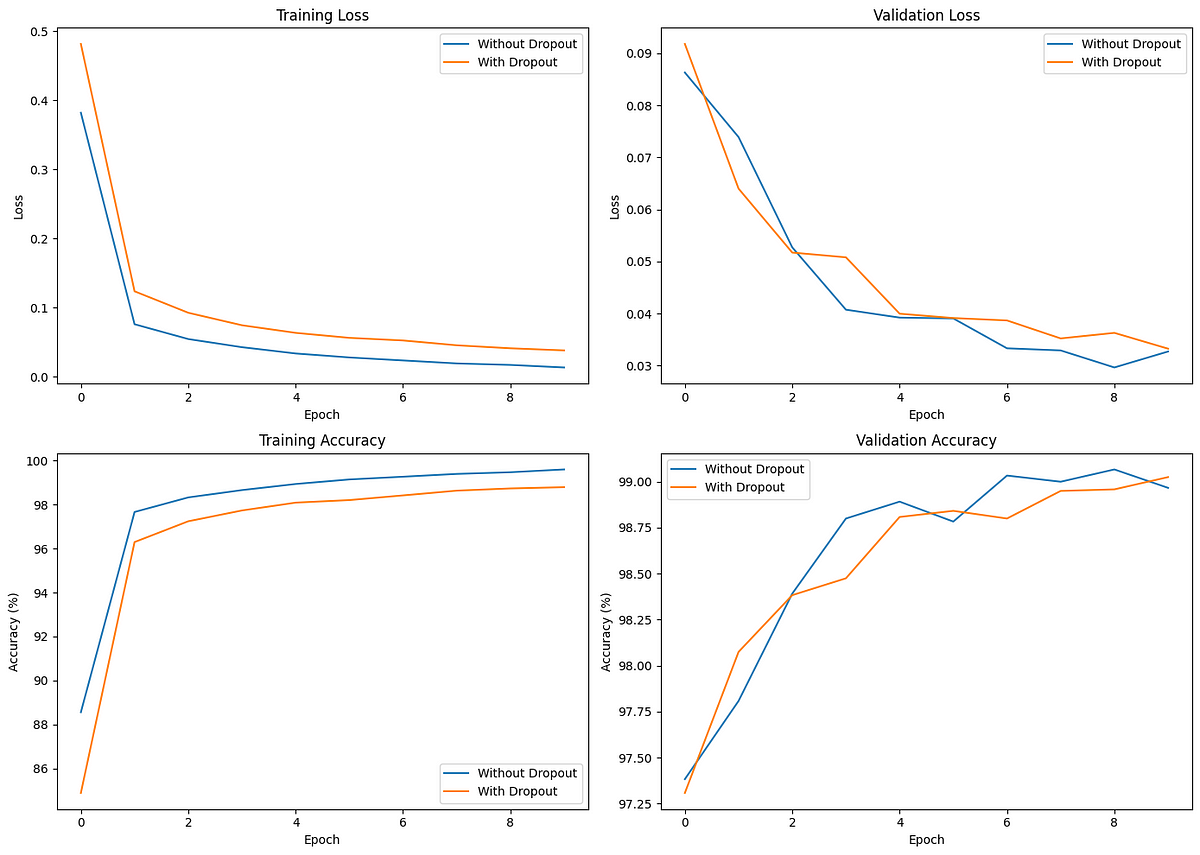
Comparar el efecto del abandono en el entrenamiento y la validación.
La pérdida de entrenamiento inicial es menor para el modelo sin abandono, lo que indica una convergencia más rápida. Sin embargo, el modelo con abandono demuestra una pérdida de validación y una precisión más consistentes, lo que indica una mejor generalización.
Al analizar estos gráficos, el modelo con abandono consigue una precisión de validación (y de prueba) ligeramente superior a la del modelo sin abandono, a pesar de que el modelo con abandono tiene una precisión de entrenamiento inferior a la del modelo sin abandono.
El abandono ayuda a evitar el sobreajuste, como se ve en la menor diferencia entre el rendimiento de entrenamiento y el de validación. Aunque insignificante en nuestro ejemplo, la diferencia se hace cada vez más crucial cuando se entrenan modelos más complejos y de mayor tamaño.
Consejos avanzados para utilizar eficazmente la regularización de abandonos
Aquí tienes algunos consejos útiles cuando entrenes modelos de aprendizaje profundo utilizando Dropout:
- Aborda primero el problema principal de tu modelo: El abandono ayuda a combatir el sobreajuste en los modelos y mejora la generalización. Si tu modelo tiene un rendimiento o un ajuste insuficientes, lo mejor es abordarlo primero cambiando los algoritmos, optimizando los hiperparámetros y, más tarde, recurriendo a la regularización por abandono si/cuando se produzca un ajuste excesivo.
- Encontrar las tasas de abandono óptimas: Nunca te conformes con una única tasa de abandono predefinida, porque los datos subyacentes que utilices pueden diferir de los que hemos utilizado en este tutorial o de los que han encontrado los investigadores. Es una buena regla general realizar varios experimentos con tasas de abandono de entre el 20% y el 50% y analizar los resultados para encontrar la tasa de abandono óptima.
- Tasas de abandono en función de la capa: Puedes aplicar la deserción a todas las capas (o a varias) en lugar de sólo a una capa oculta para obtener un mejor rendimiento de la generalización. Para las unidades de entrada, se consideró eficaz una tasa de abandono del 20% y una tasa de abandono del 50% para las unidades ocultas.
- Entrena los modelos durante muchas épocas: Añadir capas de abandono hace que el aprendizaje de patrones sea más difícil, requiriendo épocas de entrenamiento más prolongadas de lo habitual.
Si te dedicas al aprendizaje profundo, merece la pena que leas el artículo de investigación original "Mejorar las redes neuronales evitando la coadaptación de los detectores de características." En él, los autores comentan varias directrices útiles adicionales basadas en sus experimentos.
Conclusión
El sobreajuste de los datos de entrenamiento es un problema común en las redes neuronales, especialmente en los modelos más grandes entrenados para iteraciones más altas. Las técnicas de regularización, como el abandono, evitan que las redes neuronales memoricen los datos de entrenamiento y les ayudan a aprender mejor los patrones útiles de los datos.
Este tutorial introduce el concepto de regularización de abandonos, explica por qué la necesitamos y la implementa utilizando PyTorch mediante un caso de uso de ejemplo. También aprendimos algunas buenas prácticas avanzadas y consejos para utilizar eficazmente el abandono en redes neuronales profundas.
Para saber más sobre el uso de PyTorch para tareas de aprendizaje profundo, consulta el manual para principiantes Introducción al Aprendizaje Profundo con PyTorch y el curso Aprendizaje profundo intermedio con PyTorch en ese orden.