Después de recopilar datos y pasar horas limpiándolos, ¡por fin puedes empezar a explorar! Esta etapa, a menudo denominada Análisis Exploratorio de Datos (EDA), es quizá la más importante de un proyecto de datos. Los conocimientos obtenidos de EDA afectan a todo lo demás.

Por ejemplo, uno de los pasos imprescindibles en EDA es comprobar las formas de las distribuciones. Identificar correctamente la forma influye en muchas decisiones posteriores del proyecto, como:

• Otros pasos del preprocesamiento
• Realizar o no la detección de valores atípicos y, tal vez, su eliminación
• Pasos de transformación o escalado de rasgos
• Selección de características
• Selección del algoritmo

y así sucesivamente. Aunque existen visuales para realizar la tarea, necesitas métricas más fiables para cuantificar diversas características de las distribuciones. Dos de estas métricas son la asimetría y la curtosis. Puedes utilizarlas para evaluar el parecido entre tus distribuciones y una distribución normal perfecta.

Al terminar este artículo, aprenderás en detalle:

• Qué son la asimetría y la curtosis
• Los tipos de asimetría y curtosis
• El efecto de la asimetría y la curtosis en los modelos de machine learning
• Calcular la asimetría y la curtosis en Python manualmente y con paquetes de terceros
• Visualizar las distribuciones para comprobar las puntuaciones de asimetría y curtosis (sección completa y divertida)

¡Empecemos!

¿Qué es la asimetría?

Vemos la distribución normal en todas partes: medidas del cuerpo humano, pesos de objetos, puntuaciones de CI, resultados de pruebas o incluso en el gimnasio:

Fuente

Además de ser la distribución favorita de la naturaleza, es universalmente amada por casi todos los algoritmos de machine learning. Mientras que algunos quieren que mejore y estabilice su rendimiento, otros se niegan en redondo a trabajar bien con algo que no sea una distribución normal (te hablo a ti, modelos lineales).

Así que, para satisfacer la necesidad de normalidad de los algoritmos, necesitamos una forma de medir lo similares o (disímiles) que son nuestras propias distribuciones en comparación con la curva en forma de campana perfecta.

Empecemos por las colas. En una distribución normal perfecta, las colas tienen la misma longitud. Pero, cuando hay asimetría entre las colas, dándole un aspecto inclinado y aplastado hacia un lado, decimos que está sesgada. Y lo has adivinado, medimos el grado de esta asimetría con la asimetría.

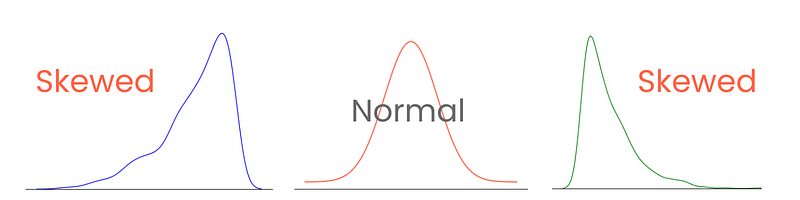
Categorizar y medir correctamente la asimetría permite comprender cómo se distribuyen los valores en torno a la media e influir en la elección de técnicas estadísticas y transformaciones de datos. Por ejemplo, las distribuciones muy sesgadas podrían beneficiarse de técnicas de normalización o escalado para asemejarlas a una distribución normal. Esto ayudaría al rendimiento del modelo.

Tipos de asimetría

Hay tres tipos de asimetría: asimetría positiva, negativa y cero.

Empecemos por la última. Una distribución con asimetría cero tiene las siguientes características:

• Distribución simétrica con valores centrados uniformemente alrededor de la media.
• No hay inclinación, inclinación o cola hacia ningún lado.
• La media, la mediana y la moda están en el punto central.

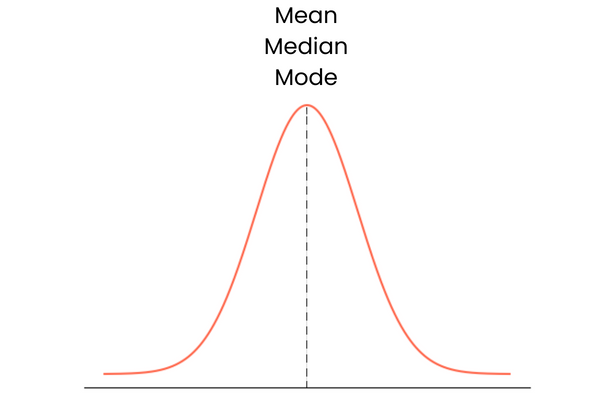
En la práctica, la media, la mediana y la moda pueden no formar una línea recta superpuesta perfecta. Podrían estar ligeramente alejados el uno del otro, pero la diferencia sería demasiado pequeña para importar.

En una distribución con asimetría positiva (sesgada a la derecha):

• La cola derecha de la distribución es más larga o más gorda que la izquierda.
• La media es mayor que la mediana, y la moda es menor que la media y la mediana.
• Los valores más bajos se agrupan en la "colina" de la distribución, mientras que los valores extremos están en la larga cola derecha.
• También se conoce como distribución sesgada a la derecha.

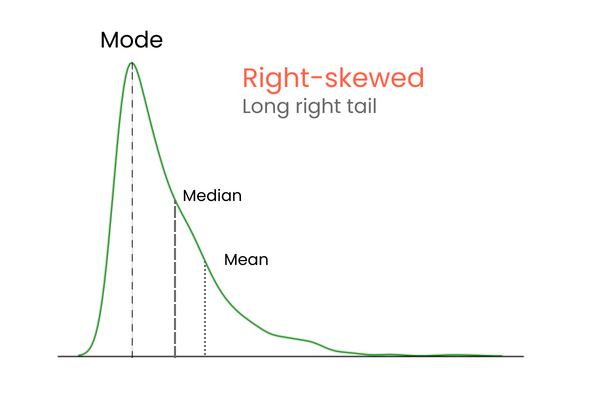
En una distribución con asimetría negativa (sesgada a la izquierda):

• La cola izquierda de la distribución es más larga o más gorda que la derecha.
• La media es menor que la mediana, y la moda es mayor que la media y la mediana.
• Los valores más altos se agrupan en la "colina" de la distribución, mientras que los valores extremos están en la larga cola izquierda.
• También se conoce como distribución sesgada a la izquierda.

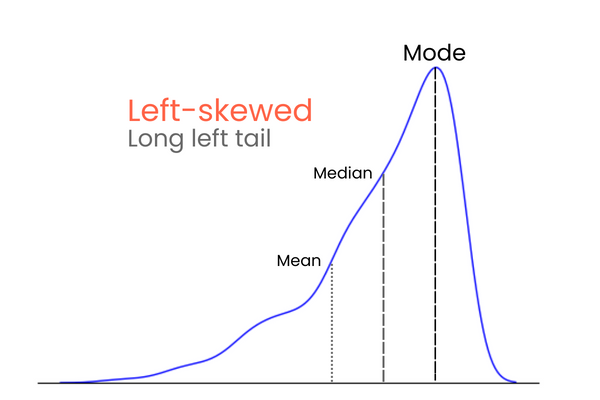
Para recordar las diferencias entre asimetría positiva y negativa, piénsalo así: si quieres aumentar la media de una distribución, debes añadir a la distribución valores mucho más altos que la media. Para bajar la media, debes hacer lo contrario: introducir en la distribución valores mucho más bajos que la media. Por tanto, si la mayoría de los valores extremos es superior a la media, la asimetría será positiva porque aumentan la media. Si la mayoría de los valores extremos es menor que la media, la asimetría es negativa porque disminuyen la media.

Cómo calcular la asimetría en Python

Hay muchas formas de calcular la asimetría, pero la más sencilla es el segundo coeficiente de asimetría de Pearson, también conocido como asimetría media.

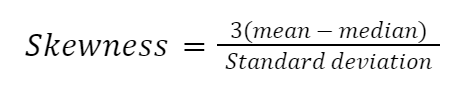
Implementemos la fórmula manualmente en Python:

import numpy as np
import pandas as pd
import seaborn as sns

# Example dataset
diamonds = sns.load_dataset("diamonds")
diamond_prices = diamonds["price"]

mean_price = diamond_prices.mean()
median_price = diamond_prices.median()
std = diamond_prices.std()

skewness = (3 * (mean_price - median_price)) / std

>>> print(
   f"The Pierson's second skewness score of diamond prices distribution is {skewness:.5f}"
)

The Pierson's second skewness score of diamond prices distribution is 1.15189

Otra fórmula muy influida por los trabajos de Karl Pearson es la fórmula basada en momentos para aproximar la asimetría. Es más fiable y se da de la siguiente manera

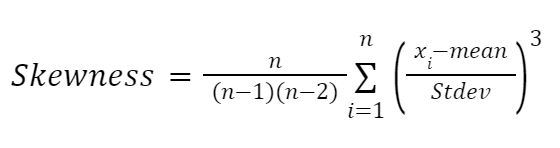
Toma:

• n representa el número de valores de una distribución
• x_i indica cada punto de datos

Implementémoslo también en Python:

def moment_based_skew(distribution):
   n = len(distribution)
   mean = np.mean(distribution)
   std = np.std(distribution)

   # Divide the formula into two parts
   first_part = n / ((n - 1) * (n - 2))
   second_part = np.sum(((distribution - mean) / std) ** 3)

   skewness = first_part * second_part

   return skewness

>>> moment_based_skew(diamond_prices)
1.618440289857168

Si no quieres calcular la asimetría manualmente (como yo), puedes utilizar los métodos integrados de pandas o scipy:

# Pandas version
diamond_prices.skew()
1.618395283383529

# SciPy version
from scipy.stats import skew

skew(diamond_prices)
1.6183502776053016

Aunque todas las fórmulas para aproximar la asimetría devuelven puntuaciones diferentes, sus diferencias son demasiado pequeñas para ser significativas o cambiar la categorización de la asimetría. Por ejemplo, todos los métodos que hemos utilizado hoy aprovechan fórmulas diferentes bajo el capó, pero los resultados son muy parecidos.

Una vez calculada la asimetría, puedes clasificar el grado de asimetría:

• (-0,5, 0,5) - bajo o aproximadamente simétrico.
• (-1, -0,5) U (0,5, 1) - moderadamente sesgada.
• Más allá de -1 y 1 - Muy sesgado.

¿Qué es la curtosis y sus tipos?

Mientras que la asimetría se centra en la dispersión (colas) de la distribución normal, la curtosis se centra más en la altura. Nos dice cómo de puntiaguda o plana es nuestra distribución normal (o similar a la normal). El término, que significa curvo o arqueado en griego, fue acuñado por primera vez, como era de esperar, por el matemático británico Karl Pearson (se pasó la vida estudiando las distribuciones de probabilidad).

Una curtosis elevada indica:

• Pico agudo en el centro de la distribución.
• Más valores concentrados en torno a la media que la distribución normal.
• Colas más pesadas debido a una mayor concentración de valores extremos o atípicos en las colas.
• Mayor probabilidad de sucesos extremos.

Por otra parte, una curtosis baja indica:

• Pico plano.
• Menos valores concentrados en torno a la media, pero aún más que la distribución normal.
• Colas más ligeras.
• Menor probabilidad de sucesos extremos.

Según el grado, las distribuciones tienen tres tipos de curtosis:

1. Distribución mesocúrtica (curtosis = 3, exceso de curtosis = 0): distribución normal perfecta o muy próxima a ella.
2. Distribución leptocúrtica (curtosis > 3, exceso de curtosis > 0): pico agudo, colas pesadas
3. Distribución platicúrtica (curtosis < 3, exceso de curtosis < 0): pico plano, colas ligeras

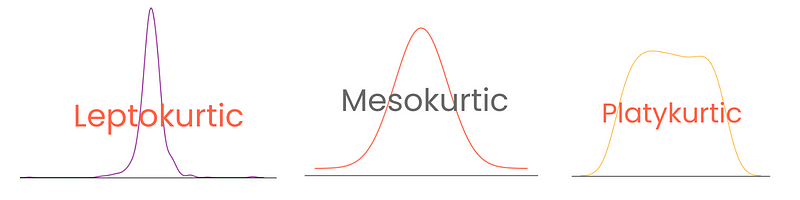
Observa que aquí, el exceso de curtosis se define como curtosis - 3, tratando la curtosis de la distribución normal como 0. De este modo, las puntuaciones de curtosis son más interpretables.

Cómo calcular la curtosis en Python

Puedes calcular la curtosis en Python del mismo modo que la asimetría utilizando pandas o SciPy:

from scipy.stats import kurtosis

kurtosis(diamond_prices)
2.177382669056634

Pandas ofrece dos funciones para la curtosis: kurt y kurtosis. La primera es exclusiva de las Series Pandas, mientras que la otra puedes utilizarla en los DataFrames.

diamond_prices.kurt()
2.17769575924869

# Select numeric features and calculate kurtosis
diamonds.select_dtypes(include="number").kurtosis()
carat     1.256635
depth     5.739415
table     2.801857
price     2.177696
x        -0.618161
y        91.214557
z        47.086619
dtype: float64

De nuevo, los números difieren para la distribución porque pandas y SciPy utilizan fórmulas diferentes.

Si quieres un cálculo manual de la curtosis, puedes utilizar la siguiente fórmula:

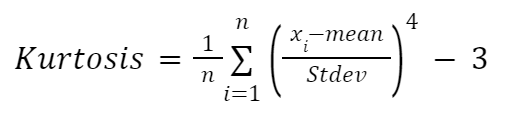
Toma:

• n representa el número de observaciones del conjunto de datos
• x_i denota cada punto de datos individual

Implementaremos de nuevo la fórmula dentro de una función:

def moment_based_kurtosis(distribution):
   n = len(distribution)
   mean = np.mean(distribution)
   std = np.std(distribution)

   kurtosis = (1 / n) * sum(((distribution - mean) / std) ** 4) - 3

   return kurtosis

>>> moment_based_kurtosis(diamond_prices)
2.1773826690576463

Y descubrimos que los precios de los diamantes tienen un exceso de curtosis de 2,18, lo que significa que si trazamos la distribución, tendrá un pico más agudo que una distribución normal.

Así que, ¡hagámoslo!

Visualizar la asimetría y la curtosis en Python

Uno de los mejores medios visuales para ver la forma y, por tanto, la asimetría y la curtosis de las distribuciones es un gráfico de estimación de la densidad del kernel (KDE). Se puede utilizar a través de Seaborn:

import matplotlib.pyplot as plt

sns.kdeplot(diamond_prices)

plt.title("KDE plot of diamond prices")
plt.xlabel("Price ($)")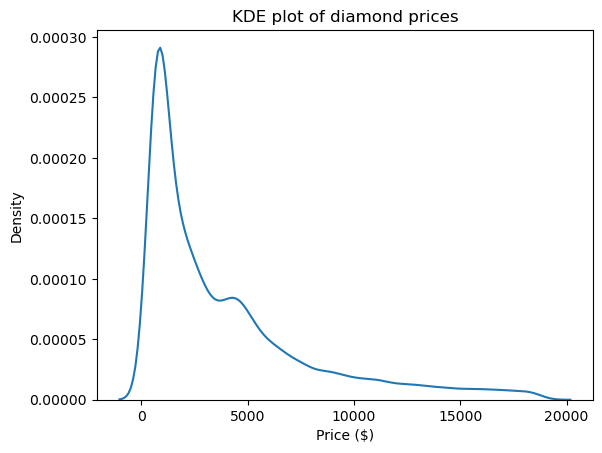

Este gráfico concuerda con las cifras que hemos visto hasta ahora: la distribución tiene una larga cola derecha, lo que indica una asimetría positiva, y tiene un pico muy agudo, que se corresponde con una curtosis elevada.

KDE no es la única parcela que ve la forma. También podemos utilizar histogramas:

sns.histplot(diamonds["carat"])

plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")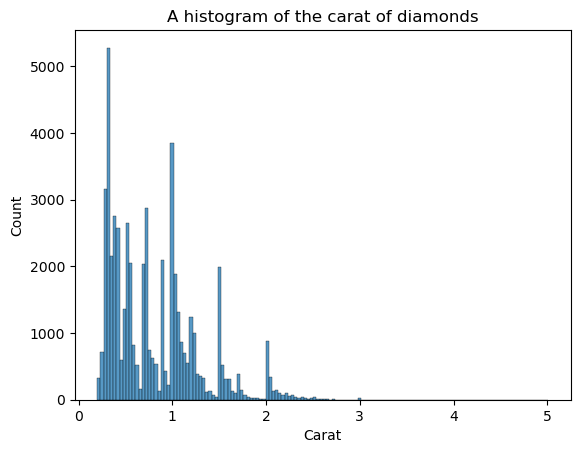

La desventaja de los histogramas es que tienes que elegir tú mismo el número de intervalos (el recuento de barras). Aquí, hay demasiadas barras que crean ruido en la visual: no podemos definir claramente la forma. Por tanto, disminuyamos el número de contenedores:

sns.histplot(diamonds["carat"], bins=25)

plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")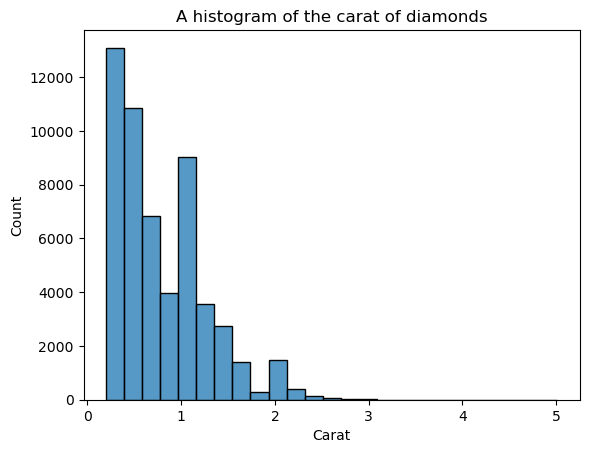

Ahora, la forma está más definida, pero podemos mejorarla más. Poniendo kde=True dentro de histplot, podemos trazar una KDE de la distribución encima de las barras:

sns.histplot(diamonds["carat"], bins=25, kde=True)

plt.xlabel("Carat")
plt.title("A histogram of the carat of diamonds")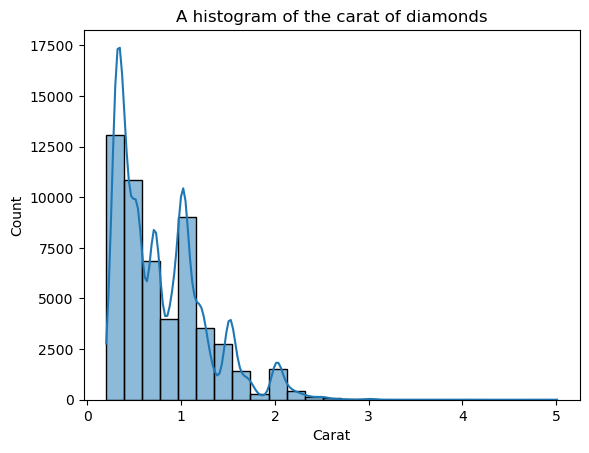

La línea KDE superpuesta parece irregular, no la curva suave que nos permite ver la forma general. La razón de la irregularidad es que la distribución de quilates es naturalmente irregular y alejada de la distribución normal.

Pero podemos disminuir la sensibilidad de la KDE a estas fluctuaciones ajustando el ancho de banda. Esto se hace utilizando el parámetro bw_adjust, que por defecto es 1:

# Change the bandwidth from 1 to 3
sns.kdeplot(diamonds["carat"], bw_adjust=3, color="red")

plt.title("KDE of diamond carats");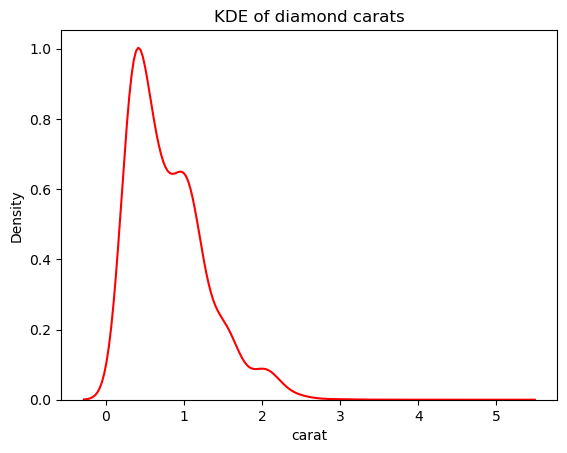

Esta versión parece mucho menos puntiaguda que el gráfico KDE superpuesto. Para ajustar el ancho de banda del KDE al utilizar un histograma superpuesto con un KDE, puedes utilizar el parámetro kde_kws:

ax = sns.histplot(
   diamonds["carat"],
   kde=True,
   kde_kws=dict(bw_adjust=3),
   bins=25,
)

plt.title("An overlaid histogram of diamond carats");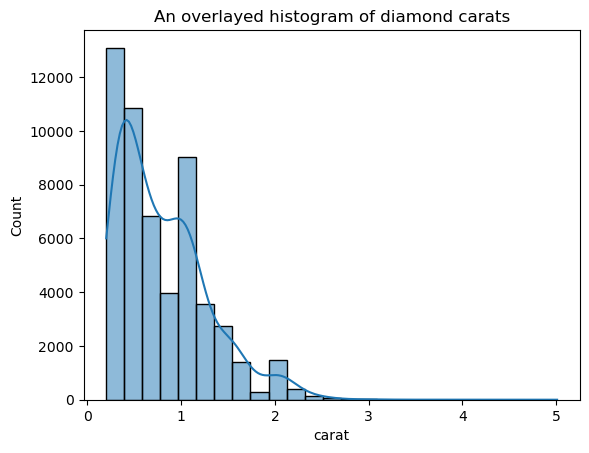

kde_kws acepta cualquier parámetro que sea aceptable por kdeplot función que controla el cálculo KDE.

Un truco que puedes utilizar al trazar KDEs es eliminar todo excepto la línea KDE. Dado que el objetivo principal de una KDE es ver la forma de la distribución, a veces son innecesarios otros detalles del gráfico, como las marcas de los ejes, las espinas y las etiquetas:

sns.kdeplot(diamond_prices, color="red")

# Remove the spine from three sides
sns.despine(top=True, right=True, left=True)

# Remove the ticks and ticklabels
plt.xticks([])
plt.yticks([])
plt.ylabel("")
plt.xlabel("")

# Set a title
plt.title("Diamond prices", fontdict=dict(fontsize=20));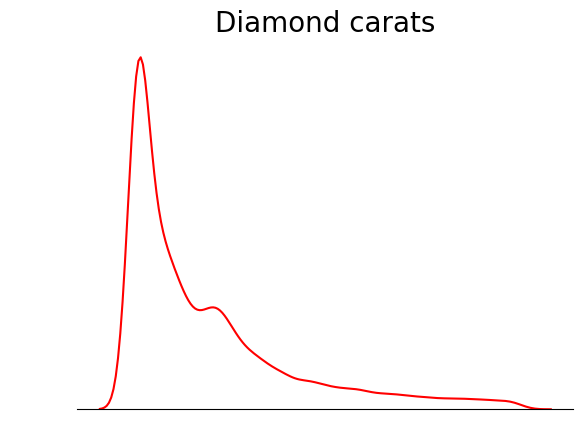

Esta parcela está mucho más ordenada. Puedes mejorar aún más el gráfico añadiendo líneas que indiquen la posición de la media, la mediana y la moda:

sns.kdeplot(diamond_prices, color="red")

sns.despine(top=True, right=True, left=True)
plt.xticks([])
plt.yticks([])
plt.ylabel("")
plt.xlabel("")
plt.title("Diamond prices", fontdict=dict(fontsize=20))

# Find the mean, median, mode
mean_price = diamonds["price"].mean()
median_price = diamonds["price"].median()
mode_price = diamonds["price"].mode().squeeze()

# Add vertical lines at the position of mean, median, mode
plt.axvline(mean_price, label="Mean")
plt.axvline(median_price, color="black", label="Median")
plt.axvline(mode_price, color="green", label="Mode")

plt.legend();

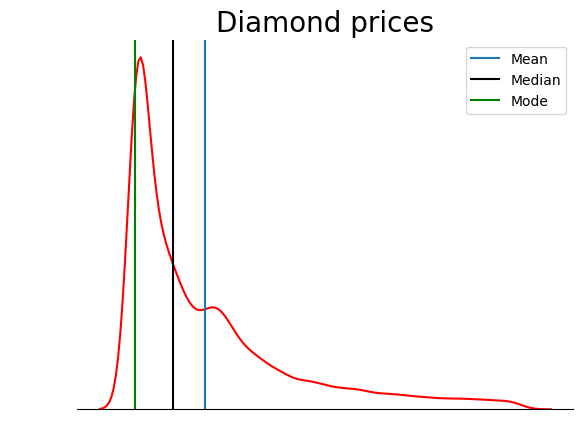
Este gráfico verifica lo que comentamos en la sección de tipos de asimetría: en una distribución sesgada positivamente, la media es mayor que la mediana, y la moda es menor que la media y la mediana.

Conclusión

La asimetría y la curtosis, que a menudo se pasan por alto en el Análisis Exploratorio de Datos, revelan importantes conocimientos sobre la naturaleza de las distribuciones.

La asimetría indica la inclinación de los datos, si se inclinan a la izquierda o a la derecha, revelando su asimetría (si la hay). La inclinación positiva significa una cola que se estira hacia la derecha, mientras que la inclinación negativa se desvía en la dirección opuesta.

La curtosis tiene que ver con picos y colas. Una curtosis alta agudiza los picos y lastra las colas, mientras que una curtosis baja dispersa los datos, aligerando las colas.

Si quieres aprender más sobre la asimetría y la curtosis, puedes consultar estos excelentes cursos de análisis cuantitativo impartidos por expertos del sector en DataCamp:

• Gestión del riesgo de cartera en Python
• Introducción al análisis de carteras en Python