Testes T no tutorial do R: Saiba como realizar testes T

Função t.test() no R

A linguagem R nos fornece uma função interna t.test simples para testes de uma amostra, duas amostras e testes t pareados. 

Há duas maneiras de usar a função t.test: métodos padrão e de fórmula. 

Método padrão 

Você fornece amostras numéricas do grupo x e do grupo y, especificando a hipótese alternativa, a média hipotética de mu e o nível de confiança do intervalo. Além disso, você pode executar o teste t pareado alternando o argumento pareado e o teste t de duas amostras com variância igual alterando o argumento var.equal. 

t.test(x, y,
      alternative = c("two.sided", "less", "greater"),
      mu = 0, paired = FALSE, var.equal = FALSE,
      conf.level = 0.95, ...)

Método de fórmula

Nesse método, você fornece a fórmula x~y, em que x é um vetor numérico ou uma coluna dos dados, e y é uma coluna binária que contém os tipos de grupos.     

t.test(formula, data, subset, na.action, ...)

Como executar o teste t de uma amostra no R

O teste t de uma amostra é a hipótese estatística para testar se há uma diferença significativa entre a média da amostra e a hipótese ou a média populacional presumida. O teste compara a média da amostra com a média da hipótese, ao mesmo tempo em que considera a variabilidade dos dados. 

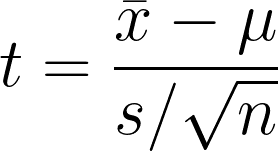
• _x̄1 = média da amostra
• μ = Média hipotética da população
• s = desvio padrão da amostra
• n = tamanho da amostra

Neste tutorial, usaremos o conjunto de dados R de absorção de dióxido de carbono em plantas de gramíneas para exemplos de código de teste t. O conjunto de dados tem 84 linhas e 5 colunas e foi coletado de um experimento para testar a tolerância ao frio da espécie de grama Echinochloa crus-galli. Consideraremos principalmente as colunas de absorção, tratamento e tipo para nossos testes. 

head(CO2)

No exemplo, usaremos a coluna conc (concentrações de dióxido de carbono) do conjunto de dados. 

Podemos observar a média, a distribuição e os outliers usando um boxplot. 

boxplot(CO2$conc)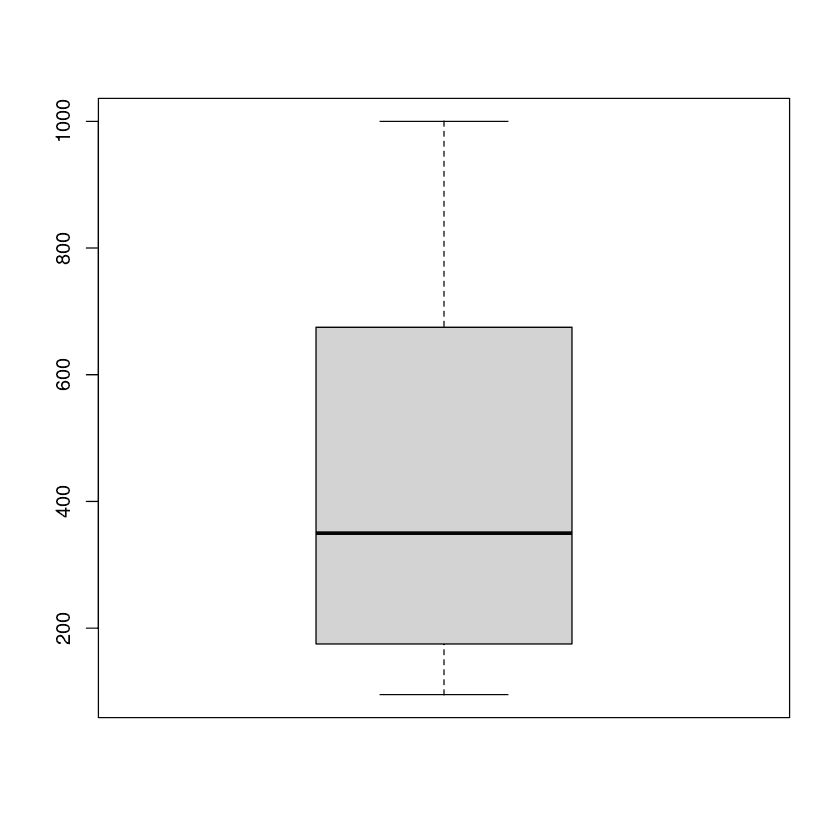

Para um teste t de uma amostra, usaremos `t.test(x,mu=0)`. Onde x é a variável, mu é definido pela hipótese nula. Em nosso caso, é 550. 

t.test(CO2$conc, mu = 550)

Resultado:

A concentração de dióxido de carbono não é igual a 550 e é significativamente menor do que a média populacional hipotética. 

One Sample t-test

data:  CO2$conc
t = -3.5617, df = 83, p-value = 0.0006134
alternative hypothesis: true mean is not equal to 550
95 percent confidence interval:
370.7805 499.2195
sample estimates:
mean of x
      435 

Como executar o teste t de duas amostras no R

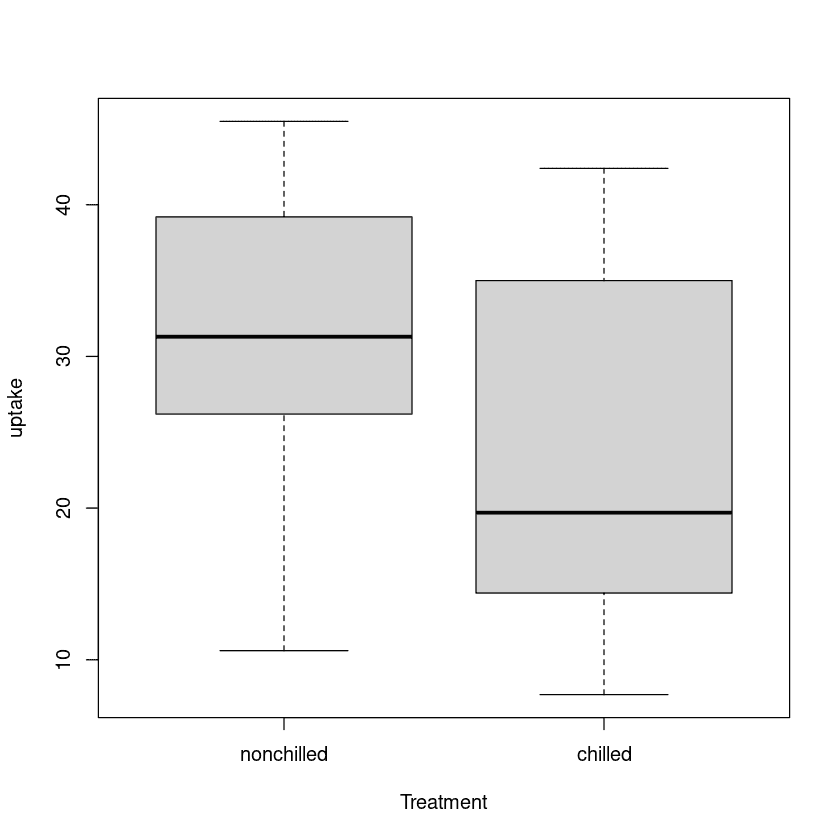
Nos testes t de duas amostras, estaremos comparando as taxas de absorção de dióxido de carbono de dois tipos de tratamento: não resfriado e resfriado. 

Podemos visualizar a distribuição de dois grupos usando um boxplot.  

plot(uptake ~ Treatment, data=CO2)

Teste t de duas amostras de Welch

É uma hipótese estatística que investiga se há uma diferença significativa entre a média de dois grupos independentes que podem ter variância desigual. O teste compara as médias de dois grupos, considerando a variabilidade dentro de cada grupo.  

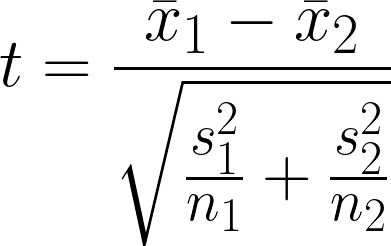
• _x̄1 = Média da amostra do primeiro grupo
• _x̄2 = Média da amostra do segundo grupo
• _n1 = Tamanho da amostra do primeiro grupo
• _n2 = tamanho da amostra do segundo grupo
• ^s12 = Variância da amostra do primeiro grupo
• ^s22 = Variância da amostra do segundo grupo

Por padrão, a função t.test() pressupõe que a variância de dois grupos é desigual (var.equal=FALSE). Portanto, não precisamos fazer nenhuma alteração. 

Estamos usando o método de fórmula para obter os resultados do teste t, em que a captação é um vetor numérico e Tratamento é uma coluna de categoria binária do conjunto de dados de CO2. 

t.test(uptake ~ Treatment, data = CO2)

Resultado:

Há uma diferença significativa nas médias dos dois grupos, e o grupo não resfriado tem maior absorção do que o grupo resfriado. 

 Welch Two Sample t-test

data:  uptake by Treatment
t = 3.0485, df = 80.945, p-value = 0.003107
alternative hypothesis: true difference in means between group nonchilled and group chilled is not equal to 0
95 percent confidence interval:
  2.382366 11.336682
sample estimates:
mean in group nonchilled    mean in group chilled
                30.64286                 23.78333  

Teste t de duas amostras com variância igual

O teste t para duas amostras é um teste estatístico de hipótese para determinar se há uma diferença significativa entre a média de dois grupos independentes, supondo que a variação dos dois grupos seja igual. O teste compara as médias de dois grupos, considerando a variabilidade dentro de cada grupo. 

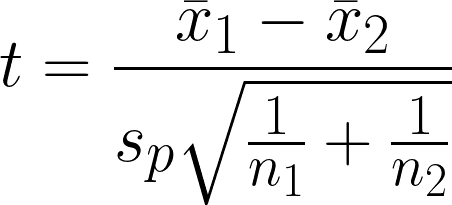
• _x̄1 = Média da amostra do primeiro grupo
• _x̄2 = Média da amostra do segundo grupo
• _n1 = Tamanho da amostra do primeiro grupo
• _n2 = tamanho da amostra do segundo grupo
• _sp = desvio padrão agrupado

Para executar testes t de duas amostras com variância igual, temos que definir var.equal TRUE e executar o teste novamente com a mesma fórmula e conjunto de dados.

t.test(uptake ~ Treatment, data = CO2, var.equal = TRUE)

Resultado:

Como podemos ver, obtivemos resultados quase semelhantes, ou seja, há uma diferença média significativa entre os dois grupos.

Two Sample t-test

data:  uptake by Treatment
t = 3.0485, df = 82, p-value = 0.003096
alternative hypothesis: true difference in means between group nonchilled and group chilled is not equal to 0
95 percent confidence interval:
  2.38324 11.33581
sample estimates:
mean in group nonchilled    mean in group chilled
                30.64286                 23.78333

Como executar o teste t pareado no R

O teste t pareado é uma hipótese estatística usada para determinar se há uma diferença significativa entre as médias de duas amostras relacionadas ou pareadas. Ele calcula o valor do teste t comparando as diferenças entre as observações emparelhadas enquanto considera a variabilidade dentro da diferença. 

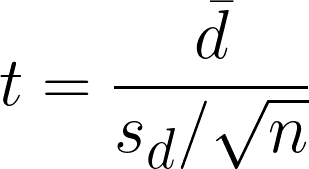
• dࠡ = diferenças de média em observações pareadas
• _sd = diferenças de desvio padrão da amostra
• n = número de pares

Para executar o teste t pareado no R, temos que definir o argumento TRUE (pareado ) e executar o teste novamente com a mesma fórmula e conjunto de dados.

t.test(uptake ~ Treatment, paired = TRUE, data = CO2)

Resultado:

Há uma diferença estatisticamente significativa entre as médias dos dois grupos, considerando o valor t e o valor p. 

Paired t-test

data:  uptake by Treatment
t = 7.939, df = 41, p-value = 8.051e-10
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
5.114589 8.604458
sample estimates:
mean difference
      6.859524 

No segundo exemplo, vamos considerar a taxa de absorção de dois tipos da mesma planta. Um deles é originário de Quebec e outro do Mississippi.

plot(uptake ~ Type, data=CO2)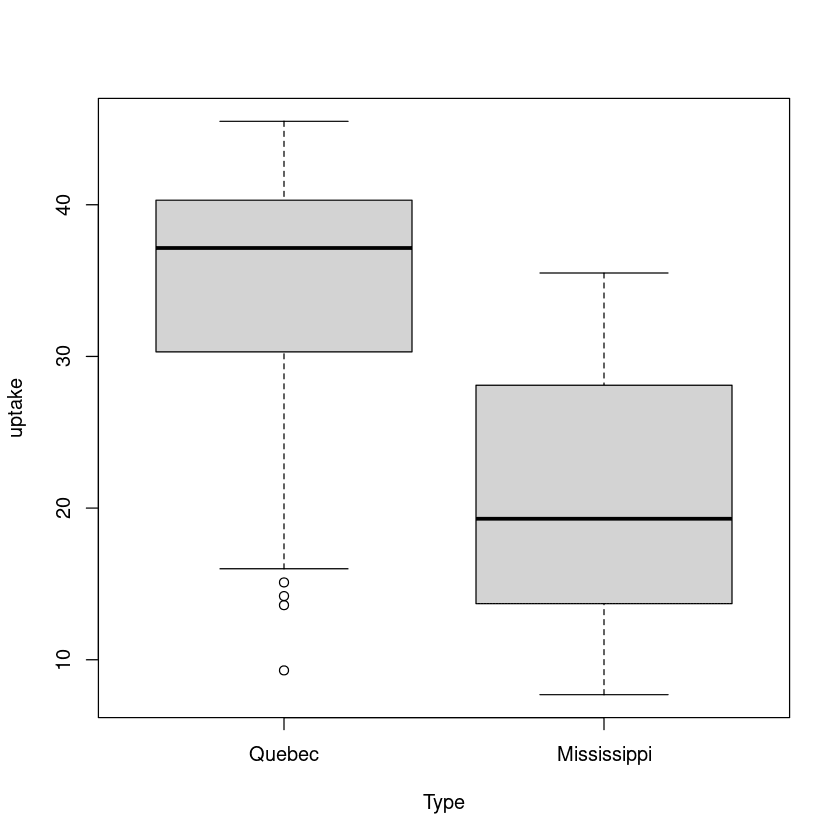

Vamos verificar os resultados do teste t pareado, substituindo o Tratamento pelo tipo na fórmula. 

t.test(uptake ~ Type, paired = TRUE, data = CO2)

Resultado:

Novamente, há uma diferença significativa entre a média do grupo de Quebec e do grupo do Mississippi. 

 Paired t-test

data:  uptake by Type
t = 11.374, df = 41, p-value = 2.937e-14
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
10.41177 14.90727
sample estimates:
mean difference
      12.65952  

Experimente o teste t no R DataLab Workbook. Ele vem com códigos-fonte e resultados. Você também pode duplicar a pasta de trabalho e começar a praticar com exemplos diferentes. 

Observação: Uma base sólida em estatística será útil para você, independentemente do setor a que pertença. A estatística é a espinha dorsal da IA moderna, e você deve começar sua jornada fazendo o curso Statistics Fundamentals with R skill track.

Como interpretar os resultados do teste t no R

Estamos gerando os resultados, mas o que significam df, p-valor, hipótese alternativa ou estimativas de amostra? Nesta seção, aprenderemos a interpretar os resultados do teste t no R. 

Vamos começar criando dois grupos usando a função rnorm e executar os testes t de duas amostras. 

set.seed(125)

group1 <- c(rnorm(100, mean = 24, sd = 3))
group2 <- c(rnorm(100, mean = 43, sd = 2.4))

t.test(group1, group2)

Saída:

 Welch Two Sample t-test

data:  group1 and group2
t = -47.765, df = 179.99, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-19.51569 -17.96722
sample estimates:
mean of x mean of y
24.30063  43.04208 

• dados: os dados usados no Two Sample t-test (grupo1 e grupo2) 
• t: t test-statistic. O valor t negativo de -47,765 indica que a média da amostra do grupo1 é significativamente menor do que a do grupo2.
• df: é o grau de liberdade associado ao valor do teste t.
• Valor de p: indica a significância estatística do resultado. O valor de p é 2,2e-16, que é menor que o alfa (0,005), indicando que a probabilidade de obter uma diferença tão grande entre os dois grupos por acaso é muito pequena.
• hipótese alternativa: podemos definir a hipótese alternativa. Em nosso caso, ele foi definido para verificar se a diferença real nas médias não é igual a zero.
• Intervalo de confiança de 95%: 95% de confiança de que a população verdadeira significa que a diferença entre os dois grupos está dentro do intervalo de -19,51569, -17,96722.
• estimativas da amostra: informa as médias da amostra de cada grupo, sendo que o grupo1 e o grupo2 são 24,30063 e 43,04208, respectivamente. Isso significa que, em média, o grupo2 tem um valor mais alto do que o grupo1. 

Há duas hipóteses para o teste t:

1. _H0: _µ1 = _µ2: as duas médias populacionais são iguais.
2. _HA: _{µ1 ≠µ2}: as duas médias populacionais não são iguais.

Em conclusão, os resultados do teste t de duas amostras de Welch sugerem que há fortes evidências de que existe uma diferença estatisticamente significativa entre o grupo1 e o grupo2. 

Conclusão 

Neste tutorial, aprendemos sobre testes de uma amostra, duas amostras e testes t pareados com exemplos de programação em R e como interpretar o resultado. 

O teste t é uma das muitas ferramentas estatísticas usadas em testes de hipóteses e, se você quiser aprender tudo sobre testes de hipóteses, faça um curso interativo de testes de hipóteses em R. O curso abrange testes t, ANOVA, testes de proporção e testes de qui-quadrado.

Você também pode ir além e se inscrever em nosso curso de carreira de Estatístico com R para dominar as habilidades essenciais e conseguir um emprego como estatístico.