Curso
La secuencia de Fibonacci es una forma divertida de seguir practicando Python. En este artículo, aprenderás a implementar la secuencia de Fibonacci en Python utilizando diferentes técnicas de Python, desde escribir funciones eficientes y manejar la recursividad hasta utilizar principios orientados a objetos para obtener soluciones más optimizadas.
Cuando hayas terminado, realiza nuestro curso Funciones de escritura en Python para reforzar conceptos como el ámbito y el manejo de errores, o prueba nuestro curso Programación orientada a objetos en Python (nivel intermedio ) para aprender sobre herencia y clases base. Ahora, probemos la secuencia de Fibonacci.
Respuesta rápida
La secuencia de Fibonacci comienza con 0 y 1, y cada número es la suma de los dos anteriores. La forma más sencilla de generarlo en Python es con un bucle:
n = 10
a, b = 0, 1
fibonacci_numbers = []
for _ in range(n):
fibonacci_numbers.append(str(a))
a, b = b, a + b
print(' '.join(fibonacci_numbers))
# This prints the first 10 Fibonacci numbers
# 0 1 1 2 3 5 8 13 21 34¿Qué es la secuencia de Fibonacci?
La secuencia de Fibonacci es un concepto matemático que aparece en muchas áreas de la ciencia y la naturaleza. Es una serie de números en la que cada número es la suma de los dos anteriores, comenzando por 0 y 1. Este patrón constituye la base para aplicaciones en campos como la informática y las finanzas.
Dos aspectos principales definen la secuencia de Fibonacci: la estructura recursiva de la secuencia y su relación con la proporción áurea.
Naturaleza recursiva de la sucesión de Fibonacci
La secuencia de Fibonacci comienza con 0 y 1. Cada nuevo número es la suma de los dos números anteriores. Por ejemplo:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
Y así sucesivamente.
Matemáticamente, lo escribimos como F(n) = F(n-1) + F(n-2). La secuencia se construye añadiendo repetidamente los dos últimos números. Los dos primeros números, 0 y 1, son el punto de partida o los casos base. Sin estos, la secuencia no funcionaría.
Este patrón recursivo sirve de base para algunos algoritmos en informática. Por ejemplo, la recursividad en programación funciona en esta secuencia cuando se resuelven problemas como generar números de Fibonacci o dividir tareas en partes más pequeñas y manejables.
Conexión con la proporción áurea
La sucesión de Fibonacci está estrechamente relacionada con la proporción áurea, que es un número irracional representado por φ (tu valor es aproximadamente 1,618). Si divides un número de Fibonacci por el anterior, la relación se acerca cada vez más a φ. Por ejemplo:
5 ÷ 3 ≈ 1,666
8 ÷ 5 ≈ 1,6
13 ÷ 8 ≈ 1,625
Cuanto más avanzas, más te acercas a 1,618. Esto no es una coincidencia: la proporción aparece de forma natural en la secuencia de Fibonacci debido a cómo crecen los números.
Euclides lo describió por primera vez en la antigua Grecia como la relación extrema y media. Desde entonces, se ha relacionado con patrones de la naturaleza, como las espirales de los terminales y las flores, así como con el arte y la arquitectura.

La proporción áurea en el arte. Fuente
Aplicaciones prácticas de la secuencia de Fibonacci
La secuencia de Fibonacci aparece de formas sorprendentes en muchos campos. Centrémonos en dos de sus aplicaciones más destacadas: sus patrones en la naturaleza y su uso en la informática.
Fibonacci en la naturaleza
La secuencia de Fibonacci se puede observar en toda la naturaleza. Fíjate en las flores: el número de pétalos suele coincidir con los números de Fibonacci. Por ejemplo, las margaritas pueden tener 34, 55 u 89 pétalos, y los lirios suelen tener 3, 5 u 8. Estos patrones ayudan a las plantas a crecer de manera que aprovechen al máximo la luz solar y las precipitaciones.
Las espirales de las piñas y los girasoles también siguen los números de Fibonacci. La disposición de las semillas en un girasol, por ejemplo, coincide con la secuencia. Es fascinante cómo algo tan simple como sumar dos números puede describir tanto del mundo natural.
Fibonacci en informática
La secuencia de Fibonacci también desempeña un papel fundamental en los algoritmos y las estructuras de datos. Por ejemplo, los números de Fibonacci se utilizan en algoritmos de búsqueda para descomponer problemas en partes más pequeñas de manera eficiente. La secuencia está incluso detrás de los montones de Fibonacci, un tipo de estructura de datos que se utiliza para acelerar ciertas operaciones, como encontrar la ruta más corta en una red.
Aquí tienes un ejemplo sencillo de cómo puedes generar una secuencia de Fibonacci en Python:
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n - 1) + fibonacci(n - 2)
# Example usage
fibonacci_numbers = []
for i in range(10):
fibonacci_numbers.append(str(fibonacci(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Esta función recursiva muestra cómo se construye la secuencia de Fibonacci. Aunque la recursividad es fácil de entender, también existen versiones optimizadas, como la programación dinámica, que permiten calcular los números de Fibonacci mucho más rápido.
En criptografía, los números de Fibonacci pueden ayudar a generar claves seguras. Y en inteligencia artificial, optimizan las redes neuronales para mejorar la forma en que los algoritmos aprenden y se adaptan.
Otros ejemplos comunes
Aquí hay algunos ejemplos más de cómo aparece esta secuencia en la vida cotidiana y en campos especializados:
- En el arte: La secuencia de Fibonacci ha sido utilizada por artistas y arquitectos durante siglos. Estructuras famosas como el Partenón presentan estas proporciones porque resultan naturalmente agradables a la vista.
- En la música: Los compositores utilizan los números de Fibonacci para crear ritmos y melodías. Por ejemplo, asignan notas enteras al 1, medias notas al 2 y cuartos de nota al 3 para crear patrones armoniosos.
- En el comercio: Los operadores bursátiles aplican los números de Fibonacci para analizar las tendencias del mercado. Los utilizan para predecir los posibles niveles de precios en los que las acciones podrían revertirse, lo que les ayuda a decidir cuándo comprar o vender.
- En Física: En la física cuántica, se han observado patrones de Fibonacci en las interacciones y el comportamiento de las partículas, lo que revela cómo estas secuencias aparecen incluso en las escalas más pequeñas de la naturaleza.
Implementación de la secuencia de Fibonacci en Python
Dado que Python ofrece varias formas de generar la secuencia de Fibonacci, he explicado paso a paso las más utilizadas con ejemplos.
Utilizando un método iterativo
El método iterativo es una de las formas más sencillas de generar la secuencia de Fibonacci. Utiliza un bucle para calcular cada término de la secuencia, lo que lo hace más eficiente en cuanto a memoria que los métodos recursivos. Así es como funciona:
He establecido dos variables, a y b, para 0 y 1. Estos representan los dos primeros números de la secuencia. A continuación, utilizo un bucle for para calcular los siguientes números. Actualizo a para que contenga el valor de b, y b se convierte en la suma de los anteriores a y b.
Aquí tienes un código Python para ello:
n = 10
a, b = 0, 1
fibonacci_numbers = []
for _ in range(n):
fibonacci_numbers.append(str(a))
a, b = b, a + b
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Si deseas utilizar un bucle « while » en lugar de un bucle « for », así es como puedes escribir el código:
# Number of terms to print in the Fibonacci series
n = 10
# Initialize the first two terms
a, b = 0, 1
i = 0
fibonacci_numbers = []
while i < n:
fibonacci_numbers.append(str(a))
# Update the terms
a, b = b, a + b
i += 1
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Ambos métodos son muy fáciles de entender, lo que los hace perfectos para principiantes.
Usando un método recursivo
El método recursivo es otra forma de generar números de Fibonacci. No es tan rápido como el método iterativo para secuencias más largas, pero es una forma estupenda de comprender la lógica que hay detrás de la construcción de la secuencia.
Por ejemplo, creamos una función llamada fibonacci_recursive. Esta función toma un número n como entrada. Si n es 0 o 1, la función devuelve n. Estos son los casos base que indican a la recursividad cuándo detenerse. Para cualquier otro número, la función se llama a sí misma para calcular los dos números anteriores y los suma.
Aquí está el código para esto:
def fibonacci_recursive(n):
if n <= 1:
return n
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
num_terms = 10
fibonacci_numbers = []
for i in range(num_terms):
fibonacci_numbers.append(str(fibonacci_recursive(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Este método funciona bien para secuencias pequeñas, pero puede volverse lento a medida que la secuencia crece, ya que recalcula los mismos valores varias veces.
Uso de un método recursivo optimizado con almacenamiento en caché
Para solucionar la ineficiencia de la recursividad simple, suelo utilizar el almacenamiento en caché. lru_cache, en Python, almacena los valores calculados previamente para que la función no tenga que volver a realizar el trabajo.
Así es como lo hago:
from functools import lru_cache
@lru_cache(maxsize = None)
def fib_cache(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib_cache(n-1) + fib_cache(n-2)
print(f"The Fibonacci Number is {fib_cache(10)}")
# The Fibonacci Number is 55Este enfoque combina la claridad de la recursividad con la eficiencia del almacenamiento en caché.
Formas más avanzadas de aplicar la secuencia de Fibonacci en Python
Si estás buscando otras formas de calcular los números de Fibonacci, aquí tienes algunas técnicas más avanzadas:
Exponenciación matricial
La exponenciación matricial es una de las formas más eficientes de calcular los números de Fibonacci para valores grandes de n. En lugar de recalcular los términos repetidamente, este método utiliza la multiplicación de matrices para obtener resultados en tiempo logarítmico.
Así es como lo implementé en Python:
import numpy as np
def fibonacci_matrix(n):
def matrix_power(matrix, power):
return np.linalg.matrix_power(matrix, power)
if n == 0:
return 0
matrix = np.array([[1, 1], [1, 0]])
result = matrix_power(matrix, n-1)
return result[0][0]
fibonacci_numbers = []
for i in range(10):
fibonacci_numbers.append(str(fibonacci_matrix(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34En este código, si n es 0, devuelve 0 como caso base. Para otros valores, la matriz se eleva a la potencia (n-1) utilizando la función matrix_power de numpy. El número de Fibonacci en la posición n se encuentra en el elemento superior izquierdo de la matriz resultante.
Fórmula de Binet
La fórmula de Binet calcula directamente el número de Fibonacci e nth e sin iteración ni recursividad. Se basa en la proporción áurea, φ, y utiliza una expresión matemática para calcular el resultado al instante.
La fórmula es:
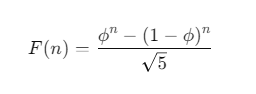
Dónde:
- φ = (1 + √5) / 2, la proporción áurea.
- 1 - φ es el conjugado de φ.
Aquí está el código Python para la fórmula de Binet:
import math
def fibonacci_binet(n):
phi = (1 + math.sqrt(5)) / 2
return round((phi ** n - (1 - phi) ** n) / math.sqrt(5))
# Find the 10th Fibonacci number
n = 10
result = fibonacci_binet(n)
print(f"The Fibonacci Number of {n}th term is {result}" )
# The Fibonacci Number of 10th term is 55En este código, la función fibonacci_binet(n) calcula el número de Fibonacci nth utilizando la fórmula de Binet. Dentro de la función, calculo phi (la proporción áurea) como (1 + math.sqrt(5)) / 2, utilizando math.sqrt() para la raíz cuadrada de 5. A continuación, se aplica la fórmula (phi ** n - (1 - phi) ** n) / math.sqrt(5) para hallar directamente el número de Fibonacci nth. A continuación, utilizo la función round() para corregir cualquier pequeña imprecisión en los números de coma flotante.
Arreglos
Incluso puedes usar arreglos para generar y almacenar toda la secuencia de Fibonacci. Esto resulta útil cuando necesitas varios términos al mismo tiempo.
Aquí está el código para esto:
def fibonacci(n):
if n <= 0:
return "Incorrect Output"
data = [0, 1] # Initialize list with first two Fibonacci terms: 0 and 1
if n > 2:
for i in range(2, n): # Start loop from the third term
data.append(data[i-1] + data[i-2]) # Calculate next term as sum of previous two
return data[n-1] # Return the nth term
print(f"Fibonacci Number: {fibonacci(10)}")
# Fibonacci Number: 34Retroceso
El backtracking es otra opción que podría utilizar, especialmente cuando quiero combinar la recursividad con la memoización para obtener un mejor rendimiento.
Aquí está el código para esto:
def fibonacci_backtracking(n, computed ={0: 0, 1: 1}):
if n in computed:
return computed[n]
computed[n] = fibonacci_backtracking(n - 1) + fibonacci_backtracking(n - 2)
return computed[n]
n = 10
result = fibonacci_backtracking(n)
print(f"The {n}th Fibonacci term is {result}")
# The 10th Fibonacci term is 55Complejidad de los algoritmos de Fibonacci en Python
¡Hemos visto bastantes ejemplos! Veamos ahora sus diferencias en términos de complejidad temporal y espacial. Como hemos mencionado, algunos métodos son rápidos pero consumen más memoria, mientras que otros son más lentos pero necesitan menos espacio. He preparado esta tabla para comparar la eficacia de cada enfoque.
| Método | Complejidad temporal | Complejidad espacial |
|---|---|---|
| Iterativo (Bucle for) | O(n) | O(1) |
| Iterativo (bucle while) | O(n) | O(1) |
| Recursividad simple | O(2ⁿ) | O(n) |
| Memorización/Almacenamiento en caché | O(n) | O(n) |
| Basado en arreglos | O(n) | O(n) |
| Método de retroceso | O(2ⁿ) | O(2ⁿ) |
| Exponenciación matricial | O(log n) | O(log n) |
En la tabla anterior, esto es lo que significa cada complejidad temporal y espacial:
-
O(n): El algoritmo recorre la secuencia una vez realizando un número fijo de operaciones para cada elemento. El tiempo que se tarda crece linealmente con el tamaño de la entrada
n. -
O(1): El número de Fibonacci se calcula utilizando un número fijo de operaciones sin iteración ni recursividad.
-
O(2n): El algoritmo realiza dos llamadas recursivas por cada entrada, lo que provoca un crecimiento exponencial del número de llamadas a la función a medida que aumenta el tamaño de la entrada (
n). -
O(log n): El tiempo de ejecución crece en proporción al logaritmo del tamaño de la entrada
n.
-
O(n): El algoritmo utiliza memoria que crece directamente con el número de entradas
n. Aquí, cada elemento requiere una cantidad fija de espacio. -
O(1): El uso de memoria permanece constante independientemente del tamaño de la entrada.
-
O(2n): Utiliza espacio exponencial debido a la creación de nuevos estados para cada rama.
-
O(log n): Las multiplicaciones de matrices intermedias utilizan memoria logarítmica.
Reflexiones finales
Como has visto, en Python se pueden calcular los números de Fibonacci utilizando muchos métodos diferentes, desde simples bucles for hasta técnicas avanzadas como la exponenciación matricial y la fórmula de Binet. Cada método tiene sus ventajas y sus inconvenientes.
Espero que hayas aprendido algo tanto sobre la secuencia de Fibonacci como sobre la programación en Python. Si deseas explorar más sobre Python y temas relacionados, consulta nuestro curso Introducción a Python. También puedes probar nuestro programa completo de programador de Python y aprender técnicas de programación, ¡e incluso empezar a desarrollar tus propios paquetes!
Soy una estratega de contenidos a la que le encanta simplificar temas complejos. He ayudado a empresas como Splunk, Hackernoon y Tiiny Host a crear contenidos atractivos e informativos para su público.
Secuencia de Fibonacci en Python Preguntas frecuentes
¿Para qué se utiliza la secuencia de Fibonacci?
La secuencia de Fibonacci se utiliza en diversos campos, como las matemáticas, la informática y los estudios sobre la naturaleza, para modelar patrones de crecimiento y optimizar algoritmos.
¿Cómo se calcula la secuencia de Fibonacci?
La secuencia de Fibonacci se calcula sumando los dos números anteriores para obtener el siguiente número, comenzando por 0 y 1.
¿Cuáles son algunos ejemplos de la secuencia de Fibonacci en la naturaleza?
Algunos ejemplos son la disposición de las hojas en un tallo, las ramas de los árboles y el patrón de diversas frutas y flores.
¿Cómo se implementa la secuencia de Fibonacci en Python?
Puedes implementarlo utilizando un enfoque iterativo o recursivo, con ejemplos de código Python disponibles en muchos tutoriales de programación.
¿Cuál es la fórmula para el enésimo término de la sucesión de Fibonacci?
El término n-ésimo se puede calcular utilizando la fórmula de Binet, que implica la proporción áurea y proporciona un método de cálculo directo.
