Cours
La suite de Fibonacci constitue une méthode intéressante pour continuer à pratiquer Python. Dans cet article, vous apprendrez à implémenter la suite de Fibonacci en Python à l'aide de différentes techniques Python, de l'écriture de fonctions efficaces et la gestion de la récursivité à l'utilisation de principes orientés objet pour des solutions plus optimisées.
Une fois que vous aurez terminé, nous vous invitons à suivre notre cours Fonctions d'écriture en Python afin de renforcer vos connaissances sur des concepts tels que la portée et la gestion des erreurs, ou à essayer notre cours Programmation orientée objet intermédiaire en Python pour en savoir plus sur l'héritage et les classes de base. Maintenant, essayons la suite de Fibonacci.
Réponse rapide
La suite de Fibonacci commence par 0 et 1, chaque nombre étant la somme des deux précédents. La manière la plus simple de le générer en Python est d'utiliser une boucle :
n = 10
a, b = 0, 1
fibonacci_numbers = []
for _ in range(n):
fibonacci_numbers.append(str(a))
a, b = b, a + b
print(' '.join(fibonacci_numbers))
# This prints the first 10 Fibonacci numbers
# 0 1 1 2 3 5 8 13 21 34Qu'est-ce que la suite de Fibonacci ?
La suite de Fibonacci est un concept mathématique qui apparaît dans de nombreux domaines scientifiques et naturels. Il s'agit d'une série de nombres où chaque nombre est la somme des deux précédents, en commençant par 0 et 1. Ce modèle constitue la base d'applications dans des domaines tels que l'informatique et la finance.
Deux aspects principaux définissent la suite de Fibonacci : la structure récursive de la suite et sa relation avec le nombre d'or.
Nature récursive de la suite de Fibonacci
La suite de Fibonacci commence par 0 et 1. Chaque nouveau nombre est la somme des deux nombres qui le précèdent. Par exemple :
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
Et ainsi de suite.
Mathématiquement, nous l'écrivons comme suit : F(n) = F(n-1) + F(n-2). La séquence se construit en ajoutant de manière répétée les deux derniers nombres. Les deux premiers nombres, 0 et 1, constituent le point de départ ou les cas de base. Sans ces éléments, la séquence ne fonctionnerait pas.
Ce modèle récursif sert de base à certains algorithmes en informatique. Par exemple, la récursivité en programmation fonctionne sur cette séquence lorsqu'il s'agit de résoudre des problèmes tels que la génération des nombres de Fibonacci ou la division de tâches en éléments plus petits et plus faciles à gérer.
Lien avec le nombre d'or
La suite de Fibonacci est étroitement liée au nombre d'or, qui est un nombre irrationnel représenté par φ (sa valeur est d'environ 1,618). Si l'on divise un nombre de Fibonacci par le nombre qui le précède, le rapport se rapproche de plus en plus de φ. Par exemple :
5 ÷ 3 ≈ 1.666
8 ÷ 5 ≈ 1.6
13 ÷ 8 ≈ 1.625
Plus vous avancez, plus vous vous rapprochez de 1,618. Ce n'est pas une coïncidence : ce rapport apparaît naturellement dans la suite de Fibonacci en raison de la manière dont les nombres augmentent.
Euclide l'a décrit pour la première fois dans la Grèce antique comme le rapport extrême et moyen. Depuis lors, il a été associé à des motifs présents dans la nature, tels que les spirales des shells et des fleurs, ainsi que dans l'art et l'architecture.

Le nombre d'or dans l'art. Source
Applications pratiques de la suite de Fibonacci
La suite de Fibonacci apparaît de manière surprenante dans de nombreux domaines. Concentrons-nous sur deux de ses applications les plus remarquables : ses motifs dans la nature et son utilisation en informatique.
Fibonacci dans la nature
La suite de Fibonacci est présente dans la nature. Observez les fleurs : le nombre de pétales correspond souvent aux nombres de Fibonacci. Par exemple, les marguerites peuvent avoir 34, 55 ou 89 pétales, et les lys en ont souvent 3, 5 ou 8. Ces modèles favorisent la croissance des plantes de manière à maximiser l'ensoleillement et les précipitations.
Les spirales des pommes de pin et des tournesols suivent également les nombres de Fibonacci. La disposition des graines dans un tournesol, par exemple, correspond à cette séquence. Il est fascinant de constater à quel point une opération aussi simple que l'addition de deux nombres peut décrire une grande partie du monde naturel.
Fibonacci en informatique
La suite de Fibonacci joue également un rôle essentiel dans les algorithmes et les structures de données. Par exemple, les nombres de Fibonacci sont utilisés dans les algorithmes de recherche pour décomposer efficacement les problèmes en parties plus petites. La séquence se trouve même derrière les tas de Fibonacci, un type de structure de données utilisé pour accélérer certaines opérations telles que la recherche du chemin le plus court dans un réseau.
Voici un exemple simple illustrant comment générer une suite de Fibonacci en Python :
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n - 1) + fibonacci(n - 2)
# Example usage
fibonacci_numbers = []
for i in range(10):
fibonacci_numbers.append(str(fibonacci(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Cette fonction récursive illustre la construction de la suite de Fibonacci. Bien que la récursivité soit facile à comprendre, il existe également des versions optimisées, telles que la programmation dynamique, qui permettent de calculer les nombres de Fibonacci beaucoup plus rapidement.
En cryptographie, les nombres de Fibonacci peuvent contribuer à générer des clés sécurisées. Dans le domaine de l'intelligence artificielle, ils optimisent les réseaux neuronaux afin d'améliorer la manière dont les algorithmes apprennent et s'adaptent.
Autres exemples courants
Voici quelques exemples supplémentaires illustrant comment cette séquence apparaît dans la vie quotidienne et dans des domaines spécialisés :
- Dans l'art : La suite de Fibonacci est utilisée par les artistes et les architectes depuis des siècles. Des structures célèbres telles que le Parthénon présentent ces proportions car elles sont naturellement agréables à l'œil.
- En musique : Les compositeurs utilisent les nombres de Fibonacci pour créer des rythmes et des mélodies. Par exemple, ils attribuent la note 1 aux notes entières, la note 2 aux demi-notes et la note 3 aux quarts de notes afin de créer des motifs harmonieux.
- Dans le domaine du trading : Les traders boursiers utilisent les nombres de Fibonacci pour analyser les tendances du marché. Ils les utilisent pour prévoir les niveaux de prix potentiels auxquels les actions pourraient s'inverser, ce qui les aide à décider quand acheter ou vendre.
- En physique : En physique quantique, des motifs de Fibonacci ont été observés dans les interactions et le comportement des particules, révélant comment ces séquences apparaissent même aux échelles les plus infimes de la nature.
Mise en œuvre de la suite de Fibonacci en Python
Étant donné que Python propose plusieurs méthodes pour générer la suite de Fibonacci, j'ai présenté les plus couramment utilisées étape par étape, accompagnées d'exemples.
Utilisation d'une méthode itérative
La méthode itérative est l'une des méthodes les plus simples pour générer la suite de Fibonacci. Il utilise une boucle pour calculer chaque terme de la séquence, ce qui le rend plus efficace en termes de mémoire que les méthodes récursives. Voici comment cela fonctionne :
J'ai défini deux variables, a et b, pour 0 et 1. Ceux-ci représentent les deux premiers nombres de la séquence. Ensuite, j'utilise une boucle « for » pour calculer les nombres suivants. Je mets à jour a pour qu'il contienne la valeur de b, et b devient la somme des valeurs précédentes a et b.
Voici un code Python pour cela :
n = 10
a, b = 0, 1
fibonacci_numbers = []
for _ in range(n):
fibonacci_numbers.append(str(a))
a, b = b, a + b
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Si vous souhaitez utiliser une boucle while au lieu d'une boucle for, voici comment écrire le code :
# Number of terms to print in the Fibonacci series
n = 10
# Initialize the first two terms
a, b = 0, 1
i = 0
fibonacci_numbers = []
while i < n:
fibonacci_numbers.append(str(a))
# Update the terms
a, b = b, a + b
i += 1
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Les deux méthodes sont extrêmement faciles à comprendre, ce qui les rend idéales pour les débutants.
Utilisation d'une méthode récursive
La méthode récursive est une autre approche pour générer les nombres de Fibonacci. Cette méthode n'est pas aussi rapide que la méthode itérative pour les séquences plus longues, mais elle constitue un excellent moyen de comprendre la logique qui sous-tend la construction de la séquence.
Par exemple, je crée une fonction appelée fibonacci_recursive. Cette fonction prend en entrée une numé n. Si n est 0 ou 1, la fonction renvoie n. Ce sont les cas de base qui indiquent à la récursivité quand s'arrêter. Pour tout autre nombre, la fonction s'appelle elle-même pour calculer les deux nombres précédents et les additionne.
Voici le code correspondant :
def fibonacci_recursive(n):
if n <= 1:
return n
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
num_terms = 10
fibonacci_numbers = []
for i in range(num_terms):
fibonacci_numbers.append(str(fibonacci_recursive(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Cette méthode est efficace pour les petites séquences, mais peut devenir lente à mesure que la séquence s'allonge, car elle recalcule les mêmes valeurs à plusieurs reprises.
Utilisation d'une méthode récursive optimisée avec mise en cache
Pour remédier à l'inefficacité de la récursivité simple, j'utilise fréquemment la mise en cache. La fonction lru_cache de Python stocke les valeurs précédemment calculées afin que la fonction n'ait pas à refaire le travail.
Voici comment je procède :
from functools import lru_cache
@lru_cache(maxsize = None)
def fib_cache(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib_cache(n-1) + fib_cache(n-2)
print(f"The Fibonacci Number is {fib_cache(10)}")
# The Fibonacci Number is 55Cette approche combine la clarté de la récursivité et l'efficacité de la mise en cache.
Méthodes plus avancées pour calculer la suite de Fibonacci en Python
Si vous recherchez d'autres méthodes pour calculer les nombres de Fibonacci, voici quelques techniques plus avancées :
Exponentiation matricielle
L'exponentiation matricielle est l'une des méthodes les plus efficaces pour calculer les nombres de Fibonacci lorsque les valeurs d'n s sont importantes. Au lieu de recalculer les termes à plusieurs reprises, cette méthode utilise la multiplication matricielle pour obtenir des résultats en temps logarithmique.
Voici comment j'ai implémenté cela en Python :
import numpy as np
def fibonacci_matrix(n):
def matrix_power(matrix, power):
return np.linalg.matrix_power(matrix, power)
if n == 0:
return 0
matrix = np.array([[1, 1], [1, 0]])
result = matrix_power(matrix, n-1)
return result[0][0]
fibonacci_numbers = []
for i in range(10):
fibonacci_numbers.append(str(fibonacci_matrix(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Dans ce code, si n correspond à 0, il renvoie ,0, etcomme cas de base. Pour les autres valeurs, la matrice est élevée à la puissance (n-1) à l'aide de la fonction matrix_power de numpy. Le nombre de Fibonacci à la position n se trouve dans l'élément supérieur gauche de la matrice résultante.
Formule de Binet
La formule de Binet permet de calculer directement le nombre de Fibonacci d'nth, sans itération ni récursivité. Il est basé sur le nombre d'or, φ, et utilise une expression mathématique pour calculer le résultat instantanément.
La formule est la suivante :
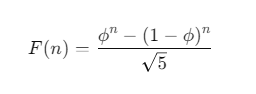
Où :
- φ = (1 + √5) / 2, le nombre d'or.
- 1 - φ est le conjugué de φ.
Voici le code Python pour la formule de Binet :
import math
def fibonacci_binet(n):
phi = (1 + math.sqrt(5)) / 2
return round((phi ** n - (1 - phi) ** n) / math.sqrt(5))
# Find the 10th Fibonacci number
n = 10
result = fibonacci_binet(n)
print(f"The Fibonacci Number of {n}th term is {result}" )
# The Fibonacci Number of 10th term is 55Dans ce code, la fonction fibonacci_binet(n) calcule le nombre de Fibonacci nth à l'aide de la formule de Binet. À l'intérieur de la fonction, je calcule phi (le nombre d'or) comme suit : (1 + math.sqrt(5)) / 2, en utilisant math.sqrt() pour la racine carrée de 5. La formule (phi ** n - (1 - phi) ** n) / math.sqrt(5) est ensuite appliquée pour déterminer directement le nombre de Fibonacci nth. Ensuite, j'utilise la fonction round() pour traiter les éventuelles petites imprécisions liées aux nombres à virgule flottante.
Tableaux
Vous pouvez également utiliser des tableaux pour générer et stocker l'intégralité de la suite de Fibonacci. Cela est utile lorsque vous avez besoin de plusieurs termes simultanément.
Voici le code correspondant :
def fibonacci(n):
if n <= 0:
return "Incorrect Output"
data = [0, 1] # Initialize list with first two Fibonacci terms: 0 and 1
if n > 2:
for i in range(2, n): # Start loop from the third term
data.append(data[i-1] + data[i-2]) # Calculate next term as sum of previous two
return data[n-1] # Return the nth term
print(f"Fibonacci Number: {fibonacci(10)}")
# Fibonacci Number: 34Retour en arrière
Le backtracking est une autre option que je pourrais utiliser, en particulier lorsque je souhaite combiner la récursivité avec la mémorisation pour améliorer les performances.
Voici le code correspondant :
def fibonacci_backtracking(n, computed ={0: 0, 1: 1}):
if n in computed:
return computed[n]
computed[n] = fibonacci_backtracking(n - 1) + fibonacci_backtracking(n - 2)
return computed[n]
n = 10
result = fibonacci_backtracking(n)
print(f"The {n}th Fibonacci term is {result}")
# The 10th Fibonacci term is 55Complexité des algorithmes de Fibonacci en Python
Nous avons examiné plusieurs exemples. Examinons maintenant leurs différences en termes de complexité temporelle et spatiale. Comme nous l'avons mentionné, certaines méthodes d's sont rapides mais utilisent davantage de mémoire, tandis que d'autres sont plus lentes mais nécessitent moins d'espace. J'ai préparé ce tableau afin de comparer l'efficacité de chaque approche.
| Méthode | Complexité temporelle | Complexité spatiale |
|---|---|---|
| Itératif (boucle for) | O(n) | O(1) |
| Itératif (boucle While) | O(n) | O(1) |
| Récursivité simple | O(2ⁿ) | O(n) |
| Mémorisation/Mise en cache | O(n) | O(n) |
| Basé sur un tableau | O(n) | O(n) |
| Méthode de retour en arrière | O(2ⁿ) | O(2ⁿ) |
| Exponentiation matricielle | O(log n) | O(log n) |
Dans le tableau ci-dessus, voici ce que signifie chaque complexité temporelle et spatiale :
-
: L'algorithme parcourt la séquence une fois en effectuant un nombre fixe d'opérations pour chaque élément. Le temps nécessaire augmente de manière linéaire avec la taille de l'entrée
n. -
O(1): Le nombre de Fibonacci est calculé à l'aide d'un nombre fixe d'opérations, sans itération ni récursivité.
-
O(2n) : L'algorithme effectue deux appels récursifs pour chaqu
n, ce qui entraîne une croissance exponentielle du nombre d'appels de fonction à mesure que l'entrée augmente. -
O(log n): La durée d'exécution augmente proportionnellement au logarithme de la taille de l'entrée
n.
-
: L'algorithme utilise une mémoire qui augmente proportionnellement au nombre d'entrées.
n. Ici, chaque élément nécessite un espace fixe. -
O(1) : L'utilisation de la mémoire reste constante quelle que soit la taille des données saisies.
-
O(2n): Il utilise un espace exponentiel en raison de la création de nouveaux états pour chaque branche.
-
O(log n): Les multiplications de matrices intermédiaires utilisent une mémoire logarithmique.
Dernières réflexions
Comme vous avez pu le constater, en Python, il est possible de calculer les nombres de Fibonacci à l'aide de nombreuses méthodes différentes, allant de simples boucles à des techniques avancées telles que l'exponentiation matricielle et la formule de Binet. Chaque méthode présente ses avantages et ses inconvénients.
J'espère que vous avez acquis des connaissances à la fois sur la suite de Fibonacci et sur la programmation Python. Si vous souhaitez approfondir vos connaissances sur Python et les sujets connexes, nous vous invitons à consulter notre cours Introduction à Python. Vous pouvez également explorer notre cursus complet de développeur Python et acquérir des techniques de programmation, voire commencer à développer vos propres packages.
Je suis un stratège du contenu qui aime simplifier les sujets complexes. J'ai aidé des entreprises comme Splunk, Hackernoon et Tiiny Host à créer un contenu attrayant et informatif pour leur public.
Séquence de Fibonacci en Python - Questions fréquentes
À quoi sert la suite de Fibonacci ?
La suite de Fibonacci est utilisée dans divers domaines, tels que les mathématiques, l'informatique et les sciences naturelles, pour modéliser des modèles de croissance et optimiser des algorithmes.
Comment la suite de Fibonacci est-elle calculée ?
La suite de Fibonacci est calculée en additionnant les deux nombres précédents pour obtenir le nombre suivant, en commençant par 0 et 1.
Quels sont les exemples de la suite de Fibonacci dans la nature ?
On peut citer comme exemples la disposition des feuilles sur une tige, la ramification des arbres et la forme de divers fruits et fleurs.
Comment implémentez-vous la suite de Fibonacci en Python ?
Vous pouvez le mettre en œuvre en utilisant une approche itérative ou récursive, avec des exemples de code Python disponibles dans de nombreux tutoriels de programmation.
Quelle est la formule pour le n-ième terme de la suite de Fibonacci ?
Le n-ième terme peut être calculé à l'aide de la formule de Binet, qui implique le nombre d'or et fournit une méthode de calcul directe.

