Notación Big O y Guía de Complejidad Temporal: Intuición y matemáticas

El análisis de la complejidad temporal proporciona una forma de analizar y predecir la eficacia de los algoritmos de una manera que es independiente tanto del lenguaje en el que los implementamos como del hardware en el que se ejecutan.

El objetivo del análisis de la complejidad temporal no es predecir el tiempo de ejecución exacto de un algoritmo, sino poder responder a estas preguntas:

1. Dados dos algoritmos que resuelven el mismo problema, ¿cuál se espera que funcione más rápido si se proporciona la misma cantidad de datos a ambos?
2. Si duplicamos los datos proporcionados al algoritmo, ¿cómo se vería afectado el tiempo de ejecución? ¿Escalará linealmente y también se duplicará? ¿Seguirá siendo igual? ¿O algo totalmente distinto?

Al final de este artículo, sabrás cómo analizar la complejidad temporal de un algoritmo y responder a estas preguntas.

¿Sigue siendo importante la complejidad temporal en 2024?

Los ordenadores son cada vez más rápidos, por lo que cabe preguntarse si ya no es necesario preocuparse por la complejidad temporal. Seguro que hoy en día un superordenador puede manejar cualquier problema independientemente del algoritmo que utilicemos para resolverlo, ¿verdad?

Bueno, no del todo. El auge de la IA se debe en gran medida a los inmensos avances en el rendimiento del hardware en los últimos años.  Sin embargo, incluso en el hardware más avanzado, problemas sencillos pueden provocar un rendimiento catastrófico si se utiliza un algoritmo lento.

Por ejemplo, imagina que utilizas un algoritmo ingenuo para ordenar una tabla de base de datos con diez millones de entradas. Incluso en un ordenador moderno, esta sencilla operación tardaría varios días en completarse, con lo que la base de datos quedaría inutilizada para cualquier aplicación práctica. En cambio, utilizando un algoritmo eficiente, podemos esperar que tarde menos de una décima de segundo.

Operaciones básicas e instrucciones básicas

Analizamos un algoritmo utilizando el modelo de Máquina de Acceso Aleatorio (RAM o RA-máquina). Este modelo supone que las siguientes operaciones duran exactamente un paso de tiempo:

• Operaciones aritméticas
• Operaciones lógicas (<, >, ==etc.)
• Declaraciones como if o return
• Acceder a una posición de memoria, como escribir o leer un valor variable

Estas operaciones se denominan operaciones básicas. Una línea de código que ejecuta un número constante de operaciones básicas se denominainstrucción básica .

Como el número de operaciones de una instrucción básica es constante, no depende de la cantidad de datos. Como lo que nos importa es cómo crece el tiempo de ejecución a medida que crece la cantidad de datos, podemos centrarnos en contar el número de instrucciones básicas que realiza el algoritmo.

Las llamadas a funciones y bucles como for y while se evalúan sumando el número de instrucciones básicas que contienen. Considera el siguiente código que suma los elementos de una lista.

def sum_list(lst):
  total = 0          # 1 instruction
  for value in lst:    
    total += value   # executed len(lst) times
  return total       # 1 instruction

Añadimos comentarios a cada línea para ayudar a visualizar el número de instrucciones básicas. Si N es la longitud de lst, entonces el número total de instrucciones básicas es 1 + N + 1 = N + 2.

Notación Big-O

Imagina que tenemos dos algoritmos de ordenación. Calculamos el número de instrucciones básicas para cada una de ellas y obtuvimos las siguientes expresiones:

A primera vista, no es obvio cuál escala mejor. La notación Big-O permite simplificar aún más estas expresiones aplicando estas simplificaciones:

1. Elimina los términos con exponentes más bajos
2. Eliminar constantes multiplicativas

Si aplicamos este proceso a ambas expresiones, obtenemos N2 en ambos casos:

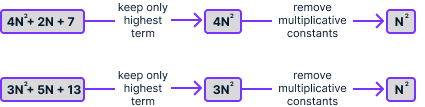
La expresión que obtenemos tras simplificar es la complejidad temporal del algoritmo, que denotamos mediante O(). En este caso, podemos escribir que 4N2 + 2N + 7 = O(N2) y 3N2 + 5N + 13 = O(N2). Esto significa que ambos algoritmos tienen la misma complejidad temporal, que es proporcional al cuadrado del número de elementos de la lista.

Anteriormente, calculamos que el algoritmo sum_list realizaba N + 2 operaciones, siendo N la longitud de la lista. Aplicando las mismas simplificaciones, obtenemos N, por lo que la complejidad temporal de sum_list es O(N).

Esto significa que el tiempo de ejecución es proporcional al tamaño de la lista. Esto es de esperar, porque al calcular la suma, duplicar el número de elementos de una lista debería requerir el doble de trabajo, no menos, ni más.

Notación Big-O: explicación intuitiva

Podemos ignorar los términos inferiores porque, a medida que N crece, su impacto en la suma total se vuelve insignificante en comparación con el término superior. El siguiente gráfico muestra la contribución de cada uno de los tres términos 4N2, 2N y 7 a la suma total.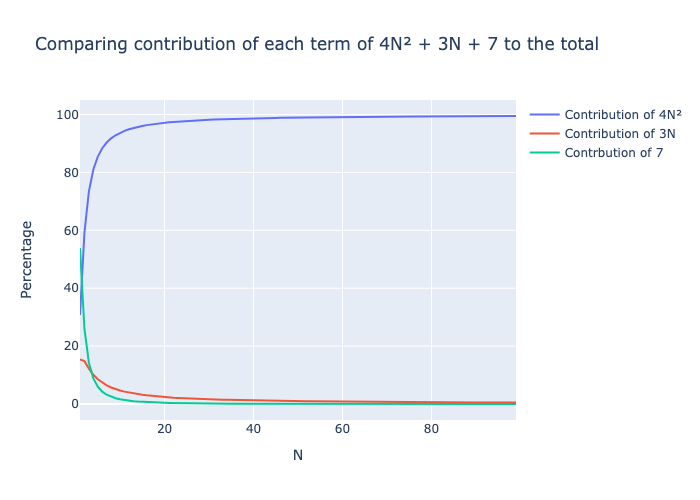

El término cuadrático 4N2 representa muy rápidamente casi el 100% del número total de operaciones, incluso para valores pequeños de N. Por tanto, cuando se trate de grandes cantidades de datos, el tiempo correspondiente a los términos de orden inferior será despreciable en comparación con los términos de orden superior.

Eliminamos la constante multiplicativa porque este valor es independiente de la cantidad de datos.

Notación Big-O: definición matemática

Para la mayoría de los fines prácticos, los pasos anteriores son suficientes para deducir con precisión la complejidad temporal de un algoritmo. Podemos contar el número de instrucciones básicas que realiza un algoritmo y obtener alguna expresión f(N). Tras aplicar los dos pasos de simplificación, obtenemos una expresión simplificada g(N). Entonces, podemos escribir que f(N) = O(g(N)). Lo leemos como "f es O grande de g".

Sin embargo, ésta no es una definición matemática formal y, en algunos casos, no es suficiente. 

La definición matemática es que una función positiva f(N) = O(g(N)) si podemos encontrar una constante C tal que, para valores grandes de N, se cumpla lo siguiente:

f(N) ≤ C × g(N)

Podemos utilizar la definición para demostrar que f(N) = 4N2 + 2N + 7 = O(N2). En este caso, podemos elegir C = 5 y ver que para cualquier N > 4, f(N) ≤ 5 × N2:

En la práctica, nos limitaremos a utilizar las reglas de simplificación anteriores.

Tipos de complejidad temporal

Ahora que entendemos lo básico de la notación Big-O, vamos a explorar las complejidades temporales más comunes y sus implicaciones, empezando por la más eficiente: el tiempo constante.

Tiempo constante: O(1)

Como su nombre indica, los algoritmos de tiempo constante tienen una complejidad temporal constante, lo que significa que su rendimiento no depende de la cantidad de datos. Estos algoritmos suelen implicar cálculos con un número fijo de entradas, como calcular la distancia entre dos puntos.

La distancia entre dos puntos se calcula calculando la raíz cuadrada de la diferencia entre las x y y de los dos puntos.

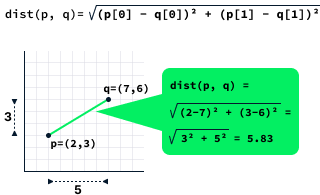
La función dist que se muestra a continuación calcula la distancia entre dos puntos. Consta de tres instrucciones básicas, que es una constante. En este caso, escribimos que la complejidad temporal es O(1).

def dist(p, q):
  dx = (p[0] - q[0]) ** 2  # 1 instruction
  dy = (p[1] - q[1]) ** 2  # 1 instruction
  return (dx + dy) ** 0.5  # 1 instruction

Curiosamente, es totalmente posible que una función muestre una complejidad temporal constante, incluso al procesar grandes conjuntos de datos. Tomemos, por ejemplo, el caso de calcular la longitud de una lista utilizando la función len. Esta operación es O(1) porque la implementación lleva internamente la cuenta del tamaño de la lista, eliminando la necesidad de contar los elementos cada vez que se solicita la longitud.

Tiempo lineal: O(N)

Ya hemos hablado anteriormente de sum_list como ejemplo de función temporal lineal. Generalmente, los algoritmos de tiempo lineal ejecutan tareas que necesitan inspeccionar cada punto de datos individualmente. Calcular el mínimo, el máximo o la media es una operación típica de esta categoría.

Practiquemos analizando la siguiente función para calcular el valor mínimo de una lista:

def minimum(lst):
  min_value = lst[0]                    # 1 instruction
  for i in range(1, len(lst)):
    min_value = min(min_value, lst[i])  # executed len(lst) - 1 times
  return min_value                      # 1 instruction

Si la lista tiene N elementos, la complejidad es 1 + (N - 1) + 1 = N + 1 = O(N).

El tiempo de ejecución de los algoritmos de tiempo lineal es directamente proporcional a la cantidad de datos. Así, si la cantidad de datos se duplica, el tiempo que tarda el algoritmo en procesarlos también debería duplicarse.

Tiempo logarítmico: O(log(N))

El juego de adivinar números consiste en intentar adivinar un número oculto entre 1 y N, con el objetivo de identificar este número con el menor número posible de aciertos. Después de cada suposición, recibimos una respuesta indicando si el número oculto es mayor, menor o igual que su suposición. Si la adivinanza es correcta, ganamos el juego; de lo contrario, seguimos adivinando.

Una estrategia eficaz para este juego es adivinar sistemáticamente el punto medio. Supongamos que N = 15. En este caso, nuestra primera suposición sería 8. Si el número secreto es menor que 8, sabemos que debe estar entre 1 y 7. Si es mayor, entonces está entre 9 y 15. Seguimos adivinando el punto medio del intervalo restante hasta que encontremos la respuesta correcta. El diagrama siguiente ilustra los posibles caminos que puede seguir esta estrategia.

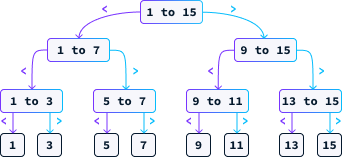
Examinemos la complejidad temporal de este planteamiento. A diferencia de los ejemplos anteriores, el número de pasos que da este algoritmo no depende únicamente del tamaño de la entrada N, ya que existe la posibilidad de acertar en el primer intento.

Al analizar estos algoritmos, nos concentramos en el peor de los casos. Por ejemplo, con N = 15, en el peor de los casos, tendríamos que hacer 4 conjeturas. Cada suposición, al ser el punto medio, elimina la mitad de las posibilidades restantes. En el peor de los casos, seguimos adivinando hasta que sólo queda una posibilidad. Por tanto, la cuestión que debemos abordar es:

¿Cuántas veces hay que dividir N entre 2 para obtener 1?

La respuesta es el logaritmo de base 2 de N, denotado como log2(N). El algoritmo utilizado para localizar el número correcto se conoce como búsqueda binaria. Dado que el número máximo de conjeturas es log2(N), podemos expresar su complejidad como O(log2(N)) o simplemente O(log(N)), ya que las constantes son insignificantes en la notación de complejidad temporal.

Debido a su tasa de crecimiento extremadamente lenta, la complejidad temporal logarítmica es muy buscada en la práctica, comportándose casi como la complejidad temporal constante. Incluso para valores grandes de N, el número total de operaciones sigue siendo notablemente bajo. Por ejemplo, aunque N sea mil millones, el número de operaciones necesarias es sólo de unas 30.

La búsqueda binaria es un algoritmo fundamental en informática con numerosas aplicaciones. Por ejemplo, en procesamiento del lenguaje naturallos correctores ortográficos y los sistemas de autocorrección pueden utilizar variantes de búsqueda binaria para identificar eficazmente posibles palabras candidatas.

Tiempo cuadrático: O(N2)

Clasificar datos es una tarea fundamental que los ordenadores deben realizar con frecuencia. Un método para ordenar una lista de N números consiste en identificar iterativamente el elemento mínimo de la lista.

def selection_sort(lst):
  sorted_lst = []              # 1 instruction
  for _ in range(len(lst)):
    minimum = min(lst)         # executed len(lst) times
    lst.remove(minimum)        # executed len(lst) times
    sorted_lst.append(minimum) # executed len(lst) times
  return sorted_lst            # 1 instruction

Para analizar la complejidad de un bucle for, evaluamos la complejidad de las instrucciones que contiene y luego multiplicamos ese resultado por el número de iteraciones que se ejecuta el bucle.

Calcular el mínimo de una lista y eliminar un elemento de una lista son operaciones O(N). La adición se realiza en tiempo constante, O(1). Por tanto, cada iteración del bucle for tiene una complejidad de O(N + N + 1) = O(2N + 1), que se simplifica a O(N). Como hay N iteraciones, la complejidad es N × O(N) = O(N2). El resto de la función selection_sort() consta de tres instrucciones simples, por lo que la complejidad global es O(N2 + 3) = O(N2).

Nuestro análisis del bucle for implicaba una simplificación excesiva. En cada iteración, eliminamos un elemento de la lista, lo que significa que no todas las iteraciones ejecutan el mismo número de instrucciones. La primera iteración ejecuta N instrucciones, la segunda ejecuta N - 1, la tercera N - 2, y este patrón continúa hasta la última iteración, que sólo ejecuta 1 instrucción.

Esto implica que la verdadera complejidad del bucle for es:

N + (N - 1) + (N - 2) + ... + 1 

Se puede demostrar que esta suma es igual a (N2 + N) / 2. Sin embargo,

(N2 + N) / 2 = ½N2 + ½N = O(N2)

Aunque hayamos contado de más, la complejidad global sigue siendo cuadrática. La función selection_sort() ejemplifica un algoritmo de ordenación más lento debido a su complejidad cuadrática, O(N2).

Las funciones con complejidad cuadrática escalan mal, lo que las hace adecuadas para listas pequeñas, pero poco prácticas para ordenar millones de puntos de datos, ya que pueden tardar días en completar la tarea. Duplicar la cantidad de datos lleva a cuadruplicar el tiempo de ejecución.

Tiempo logarítmico: O(N log(N))

Es posible idear un algoritmo para ordenar una lista con complejidad temporal O(N log(N)). Uno de estos algoritmos se llama merge sort.  No vamos a entrar en los detalles de su implementación, pero si quieres saber más sobre ella, consulta esta introducción rápida a la ordenación por fusión de este curso sobre Estructuras de Datos y Algoritmos en Python.

Como ya se ha dicho, la complejidad logarítmica se comporta en la práctica de forma similar a la complejidad constante. Por tanto, el tiempo de ejecución de un algoritmo O(N log(N)) puede ser comparable al de un algoritmo de tiempo lineal en aplicaciones del mundo real.

El siguiente gráfico muestra que N log(N) y N crecen a ritmos similares, mientras que N2 crece muy rápido, convirtiéndose rápidamente en muy lento.

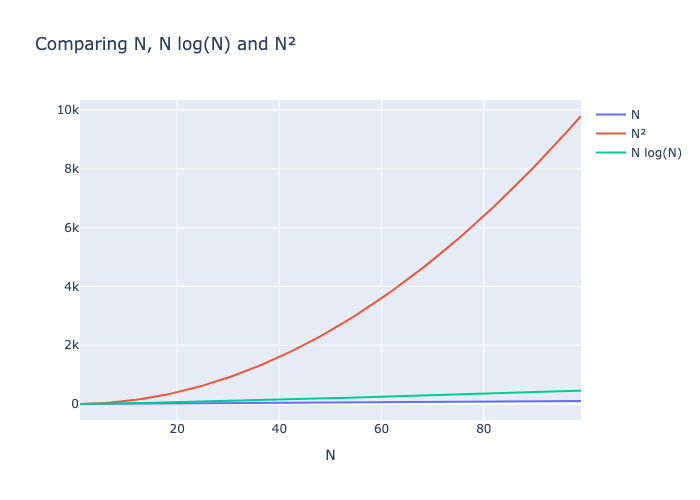
Tiempo cúbico: O(N3)

Un algoritmo de complejidad temporal cúbica muy utilizado en la IA es la multiplicación de matrices, que desempeña un papel crucial en la funcionalidad de grandes modelos lingüísticos como el GPT. Este algoritmo es fundamental para los cálculos que se realizan tanto en la fase de entrenamiento como en la de inferencia.

Para multiplicar dos matrices de N por N, A y B, necesitamos multiplicar cada fila de la primera matriz A por cada columna de la segunda matriz B. Concretamente, el valor del producto en la entrada (i, j) se determina multiplicando los elementos de la fila i de A por los elementos correspondientes de la columna j de B.

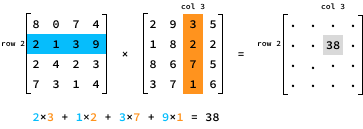
Aquí tienes una implementación en Python de la multiplicación de matrices:

def matrix_mul(A, B):
  n = len(A)                                       # 1 instruction
  res = [[0 for _ in range(n)] for _ in range(n)]  # N^2 instructions
  for i in range(n):
    for j in range(n):
      for k in range(n):
        res[i][j] += A[i][k] * B[k][j]             # executed N×N×N = N^3 times
  return res                                       # 1 instruction

En total, matrix_mul() ejecuta N3 + N2 + 2 instrucciones, por lo que su complejidad temporal es O(N3).

Alternativamente, podríamos haber analizado la complejidad razonando sobre los cálculos. El resultado de la multiplicación de matrices tiene N2 entradas. Cada entrada tarda O(N) en calcularse, por lo que la complejidad global es N2 × O(N) = O(N3).

Los algoritmos de tiempo cúbico son bastante lentos. Duplicar la cantidad de datos multiplica por ocho el tiempo de ejecución, lo que hace que estos algoritmos sean muy poco escalables. Incluso para un valor relativamente pequeño de N, el número de instrucciones explota muy rápidamente.

La multiplicación de matrices es un ejemplo de reto computacional en el que los avances en hardware han tenido un impacto significativo. Aunque existen algoritmos algo más eficientes para la multiplicación de matrices, son principalmente los avances en el diseño de chips de GPU -adaptados específicamente para realizar la multiplicación de matrices- los que han facilitado notablemente el entrenamiento de grandes modelos como el GPT en plazos razonables.

Más recientemente, los investigadores han propuesto eliminar la multiplicación matricial de los grandes modelos de aprendizaje; puedes leer más sobre esto en este artículo sobre LLMs sin MatMul: Explicación de los conceptos clave.

Complejidad temporal exponencial: O(2N) y O(N!)

Los algoritmos de tiempo exponencial suelen surgir cuando un problema se resuelve explorando todas las soluciones posibles. Considera la posibilidad de planificar una ruta para un camión de reparto que tenga que visitar N lugares de reparto. Una forma de abordar este problema es evaluar todas las órdenes de entrega posibles. El programa Python itertools paquete ofrece un método sencillo para recorrer todas las permutaciones de una lista.

import itertools
for order in itertools.permutations([1, 2, 3]):
  print(order)

(1, 2, 3)
(1, 3, 2)
(2, 1, 3)
(2, 3, 1)
(3, 1, 2)
(3, 2, 1)

El número de permutaciones de una lista de longitud N se denota por N!, que se lee como "N factorial". La función factorial presenta un crecimiento exponencial. Por ejemplo, cuando N = 13, el número de permutaciones supera los 1.000 millones.

Supongamos que los lugares de entrega se dan como una lista de puntos 2D. En ese caso, podemos determinar la secuencia de entrega que minimiza la distancia total iterando a través de todas las secuencias posibles sin perder de vista la mejor.

def optimize_route(locations):
  minimum_distance = float("inf")                  # 1 instruction
  best_order = None                                # 1 instruction
  for order in itertools.permutations(locations):  # N! iterations
    distance = 0                                   # 1 instruction, N! times
    for i in range(1, len(order)):                 
      distance += dist(order[i - 1], order[i])     # N-1 instructions, N! times
    if distance < minimum_distance:                
      distance = minimum_distance                  # 1 instruction, N! times
      best_order = order                           # 1 instruction, N! times
  return best_order                                # 1 instruction

El primer bucle for se ejecuta N! veces. Por tanto, el número de operaciones en optimize_route() es N! x (1 + N - 1 + 2) + 3 = N! x (N + 2) + 3 = N! x N + 2N! + 3.

Hemos aprendido que, al calcular la complejidad temporal, ignoramos los términos de exponente inferior. Sin embargo, en este escenario, nos encontramos con un término N!, que no es una potencia de N. Podemos refinar nuestra estrategia de simplificación optando por omitir los términos con tasas de crecimiento más lentas. La tabla siguiente enumera los términos que suelen aparecer en la complejidad temporal de un algoritmo, ordenados de menor a mayor tasa de crecimiento.

Así, podemos expresar la complejidad temporal de optimize_route() como N! x N + 2N! + 3 = O(N! x N).

Los algoritmos de complejidad en tiempo exponencial sólo suelen ser eficientes para resolver instancias muy pequeñas. Incluso con sólo 13 ubicaciones, el número de permutaciones supera los 1.000 millones, lo que hace que este algoritmo sea poco práctico para los escenarios del mundo real.

Complejidad temporal: Peor caso y mejor caso

Con el juego de adivinar números, nos centramos en la complejidad del peor caso. Al centrarnos en el peor caso, garantizamos la tasa de crecimiento del tiempo de ejecución del algoritmo.

En el mejor de los casos, adivinamos la primera vez, por lo que un análisis de complejidad en el mejor de los casos daría como resultado una complejidad O(1). Esto es exacto: en el mejor de los casos, necesitamos una sola operación constante. Sin embargo, esto no es del todo útil porque es muy poco probable.

En general, cuando analizamos la complejidad de un algoritmo, siempre nos centramos en el peor de los casos porque:

1. Garantía de cumplimiento: Al centrarnos en la complejidad del peor caso, podemos garantizar que nuestro algoritmo nunca obtendrá peores resultados que un determinado umbral. Esto es crucial para las aplicaciones que requieren un rendimiento fiable, como los sistemas en tiempo real, donde los retrasos pueden causar problemas importantes.
2. Seguridad y fiabilidad: El análisis del peor de los casos ayuda a diseñar algoritmos robustos que puedan manejar los escenarios más exigentes. Garantiza que el algoritmo seguirá funcionando dentro de unos límites aceptables incluso en las peores situaciones posibles.
3. Límite superior: Conocer la complejidad en el peor de los casos nos da un límite superior del rendimiento. Esto es útil para conocer los recursos máximos (tiempo, memoria) que puede necesitar un algoritmo.

Complejidad temporal: Implicaciones prácticas

La complejidad temporal puede parecer un tema muy teórico, pero puede resultar muy útil en la práctica.

Por ejemplo, si una función maneja sistemáticamente un conjunto de datos pequeño, un O(N2) puede ser más apropiado que un algoritmo O(N) complejo y difícil de mantener. Sin embargo, ésta debe ser una decisión deliberada para evitar que te cojan desprevenido cuando la aplicación no pueda soportar un aumento del tráfico de usuarios.

El análisis de la complejidad temporal revela que las optimizaciones menores del código tienen un efecto insignificante en el tiempo de ejecución de un algoritmo. Se consiguen mejoras significativas reduciendo fundamentalmente el número de operaciones básicas necesarias para calcular el resultado. En general, es preferible mantener un código limpio y comprensible que optimizarlo hasta hacerlo ininteligible.

Las partes más lentas del código dominarán a las demás. Suele ser inútil optimizar la parte más rápida antes de optimizar la más lenta. Por ejemplo, imagina que tenemos una función que realiza dos tareas:

def process_data(data):
  clean_data(data)
  analyze_data(data)

Si la función clean_data() tiene una complejidad O(N2) y analyze_data() tiene una complejidad O(N3), entonces reducir la complejidad de clean_data() no mejorará la complejidad global de process_data(). Es mejor centrarse en mejorar la función analyze_data().

Además, la complejidad temporal puede informar sobre las decisiones de hardware. Por ejemplo, un O(N3), a pesar de su escasa escalabilidad, podría seguir siendo lo suficientemente rápido para tareas con datos limitados si se ejecuta en un hardware superior o en un lenguaje de programación más rápido. A la inversa, si un algoritmo tiene una complejidad temporal exponencial O(2N), no bastará ninguna mejora del hardware, lo que indica la necesidad de un algoritmo más eficiente.

Conclusión

A pesar de que los ordenadores son cada vez más rápidos, tratamos con más datos que nunca. Piénsalo así: cada vez que utilizamos Internet, teléfonos inteligentes o dispositivos domésticos inteligentes, creamos toneladas de información. A medida que crece esta montaña de datos, clasificarlos y encontrar lo importante se hace más difícil. Por eso es muy importante seguir mejorando nuestras herramientas -especialmente los algoritmos- para manejar y comprender toda esta información.

El análisis de la complejidad temporal ofrece un marco sencillo para razonar sobre el tiempo de ejecución de un algoritmo. Su objetivo principal es proporcionar información sobre la tasa de crecimiento de la complejidad temporal, en lugar de predecir los tiempos exactos de ejecución. A pesar de las numerosas simplificaciones y suposiciones del modelo, ha demostrado ser extremadamente útil en la práctica, captando eficazmente la esencia de los comportamientos del tiempo de ejecución de los algoritmos.

Si quieres explorar más temas de informática, consulta mi artículo sobre Estructuras de datos: Una guía completa con ejemplos de Python.