Kurs
Einführung in Python
4 Std.
6.5M
Die Fibonacci-Folge ist eine coole Möglichkeit, um weiter Python zu üben. In diesem Artikel lernst du, wie du die Fibonacci-Folge in Python mit verschiedenen Python-Techniken umsetzt, vom Schreiben effizienter Funktionen über den Umgang mit Rekursion bis hin zur Verwendung objektorientierter Prinzipien für optimierte Lösungen.
Wenn du fertig bist, mach unseren Kurs Schreibfunktionen in Python, um Konzepte wie Geltungsbereich und Fehlerbehandlung zu vertiefen, oder probier unseren Kurs Objektorientierte Programmierung in Python für Fortgeschrittene aus, um mehr über Vererbung und Basisklassen zu lernen. Probieren wir jetzt mal die Fibonacci-Folge aus.
Schnelle Antwort
Die Fibonacci-Folge fängt mit 0 und 1 an, wobei jede Zahl die Summe der beiden vorherigen ist. Der einfachste Weg, das in Python zu machen, ist mit einer Schleife:
n = 10
a, b = 0, 1
fibonacci_numbers = []
for _ in range(n):
fibonacci_numbers.append(str(a))
a, b = b, a + b
print(' '.join(fibonacci_numbers))
# This prints the first 10 Fibonacci numbers
# 0 1 1 2 3 5 8 13 21 34Was ist die Fibonacci-Folge?
Die Fibonacci-Folge ist ein mathematisches Konzept, das in vielen Bereichen der Wissenschaft und Natur vorkommt. Es ist eine Reihe von Zahlen, bei der jede Zahl die Summe der beiden vorherigen ist, angefangen mit 0 und 1. Dieses Muster ist die Basis für Anwendungen in Bereichen wie Informatik und Finanzen.
Zwei Hauptaspekte machen die Fibonacci-Folge aus: die rekursive Struktur der Folge und ihre Verbindung zum Goldenen Schnitt.
Rekursive Natur der Fibonacci-Folge
Die Fibonacci-Folge fängt mit 0 und 1 an. Jede neue Zahl ist die Summe der beiden Zahlen davor. Zum Beispiel:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
Und so weiter.
Mathematisch gesehen schreiben wir das so: F(n) = F(n-1) + F(n-2). Die Folge entsteht, indem man immer die letzten beiden Zahlen zusammenzählt. Die ersten beiden Zahlen, 0 und 1, sind der Startpunkt oder die Basisfälle. Ohne die würde die Sequenz nicht funktionieren.
Dieses rekursive Muster ist die Grundlage für einige Algorithmen in der Informatik. Zum Beispiel wird Rekursion in der Programmierung bei dieser Sequenz benutzt, wenn man Probleme wie die Erzeugung von Fibonacci-Zahlen löst oder Aufgaben in kleinere, überschaubare Teile aufteilt.
Verbindung zum Goldenen Schnitt
Die Fibonacci-Folge hängt eng mit dem Goldenen Schnitt zusammen, einer irrationalen Zahl, die mit φ dargestellt wird (ihr Wert liegt bei etwa 1,618). Wenn du eine Fibonacci-Zahl durch die vorherige teilst, kommt das Verhältnis immer näher an φ ran. Zum Beispiel:
5 ÷ 3 ≈ 1.666
8 ÷ 5 ≈ 1,6
13 ÷ 8 ≈ 1.625
Je weiter du kommst, desto näher kommst du an 1,618heran . Das ist kein Zufall – dieses Verhältnis kommt in der Fibonacci-Folge ganz natürlich vor, weil die Zahlen so wachsen.
Euklid hat es im alten Griechenland als extremes und mittleres Verhältnis beschrieben. Seitdem wird es mit Mustern in der Natur, wie den Spiralen in shells und Blumen, sowie in der Kunst und Architektur in Verbindung gebracht.
Der Goldene Schnitt in der Kunst. Quelle
Praktische Anwendungen der Fibonacci-Folge
Die Fibonacci-Folge taucht auf überraschende Weise in vielen Bereichen auf. Schauen wir uns mal zwei der coolsten Anwendungen an: die Muster in der Natur und wie es in der Informatik genutzt wird.
Fibonacci in der Natur
Die Fibonacci-Folge findest du überall in der Natur. Schau dir Blumen an – die Anzahl der Blütenblätter passt oft zu den Fibonacci-Zahlen. Zum Beispiel können Gänseblümchen 34, 55 oder 89 Blütenblätter haben, und Lilien haben oft 3, 5 oder 8. Diese Muster helfen den Pflanzen, so zu wachsen, dass sie möglichst viel Sonnenlicht und Regen abbekommen.
Auch die Spiralen in Tannenzapfen und Sonnenblumen folgen den Fibonacci-Zahlen. Die Anordnung der Samen in einer Sonnenblume passt zum Beispiel zu dieser Reihenfolge. Es ist echt faszinierend, wie etwas so Einfaches wie das Addieren von zwei Zahlen so viel über die Natur erzählen kann.
Fibonacci in der Informatik
Die Fibonacci-Folge ist auch super wichtig für Algorithmen und Datenstrukturen. Zum Beispiel werden Fibonacci-Zahlen in Suchalgorithmen verwendet, um Probleme effizient in kleinere Teile zu zerlegen. Die Sequenz steht sogar hinter Fibonacci-Heaps, einer Art von Datenstruktur, die bestimmte Vorgänge beschleunigt, wie zum Beispiel das Finden des kürzesten Weges in einem Netzwerk.
Hier ist ein einfaches Beispiel, wie du eine Fibonacci-Folge in Python erstellen kannst:
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n - 1) + fibonacci(n - 2)
# Example usage
fibonacci_numbers = []
for i in range(10):
fibonacci_numbers.append(str(fibonacci(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Diese rekursive Funktion zeigt, wie die Fibonacci-Folge aufgebaut ist. Rekursion ist zwar leicht zu verstehen, aber es gibt auch optimierte Versionen wie die dynamische Programmierung, mit denen man Fibonacci-Zahlen viel schneller berechnen kann.
In der Kryptografie können Fibonacci-Zahlen dabei helfen, sichere Schlüssel zu generieren. Und in der künstlichen Intelligenz optimieren sie neuronale Netze, um das Lernen und die Anpassung von Algorithmen zu verbessern.
Andere gängige Beispiele
Hier sind noch ein paar Beispiele, wie diese Reihenfolge im Alltag und in speziellen Bereichen vorkommt:
- In der Kunst: Die Fibonacci-Folge wird schon seit Ewigkeiten von Künstlern und Architekten genutzt. Berühmte Bauwerke wie der Parthenon haben diese Proportionen, weil sie einfach schön anzusehen sind.
- In der Musik: Komponisten nutzen Fibonacci-Zahlen, um Rhythmen und Melodien zu machen. Zum Beispiel ordnen sie ganzen Noten den Wert 1, halben Noten den Wert 2 und Viertelnoten den Wert 3 zu, um harmonische Muster zu schaffen.
- Beim Handel: Börsenhändler nutzen Fibonacci-Zahlen, um Markttrends zu checken. Sie nutzen sie, um mögliche Kursniveaus vorherzusagen, bei denen sich die Aktien umkehren könnten, was ihnen hilft, zu entscheiden, wann sie kaufen oder verkaufen sollen.
- In der Physik: In der Quantenphysik hat man Fibonacci-Muster bei den Wechselwirkungen und dem Verhalten von Teilchen gesehen, was zeigt, wie diese Sequenzen sogar auf den kleinsten Ebenen der Natur auftauchen.
Die Fibonacci-Folge in Python umsetzen
Da Python mehrere Möglichkeiten bietet, die Fibonacci-Folge zu generieren, habe ich die am häufigsten verwendeten Methoden Schritt für Schritt mit Beispielen erklärt.
Mit einer iterativen Methode
Die iterative Methode ist eine der einfachsten Möglichkeiten, die Fibonacci-Folge zu erzeugen. Es nutzt eine Schleife, um jeden Term in der Folge zu berechnen, was es speichereffizienter macht als rekursive Methoden. So läuft's ab:
Ich habe zwei Variablen, a und b, auf 0 und 1. Das sind die ersten beiden Zahlen in der Reihe. Dann benutze ich eine Schleife for, um die nächsten Zahlen zu berechnen. Ich aktualisiere a, damit es den Wert von b enthält, und b wird zur Summe aus dem vorherigen a und b.
Hier ist ein Python-Code dafür:
n = 10
a, b = 0, 1
fibonacci_numbers = []
for _ in range(n):
fibonacci_numbers.append(str(a))
a, b = b, a + b
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Wenn du eine Schleife while anstelle einer Schleife for verwenden möchtest, kannst du den Code wie folgt schreiben:
# Number of terms to print in the Fibonacci series
n = 10
# Initialize the first two terms
a, b = 0, 1
i = 0
fibonacci_numbers = []
while i < n:
fibonacci_numbers.append(str(a))
# Update the terms
a, b = b, a + b
i += 1
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Beide Methoden sind superleicht zu verstehen, was sie perfekt für Anfänger macht.
Mit einer rekursiven Methode
Die rekursive Methode ist eine andere Möglichkeit, Fibonacci-Zahlen zu erzeugen. Bei längeren Reihen ist das nicht so schnell wie die iterative Methode, aber es ist super, um zu verstehen, wie die Reihe aufgebaut ist.
Ich mache zum Beispiel eine Funktion namens fibonacci_recursive. Diese Funktion braucht eine Zahlen n, als Eingabe. Wenn n 0 oder 1 ist, gibt die Funktion n zurück. Das sind die Basisfälle, die der Rekursion sagen, wann sie aufhören soll. Für jede andere Zahl ruft die Funktion sich selbst auf, um die beiden vorherigen Zahlen zu berechnen, und addiert sie.
Hier ist der Code dafür:
def fibonacci_recursive(n):
if n <= 1:
return n
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
num_terms = 10
fibonacci_numbers = []
for i in range(num_terms):
fibonacci_numbers.append(str(fibonacci_recursive(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34Diese Methode klappt gut bei kleinen Sequenzen, kann aber mit zunehmender Länge der Sequenz langsam werden, weil sie dieselben Werte mehrmals neu berechnet.
Mit einer optimierten rekursiven Methode mit Caching
Um die Ineffizienz der einfachen Rekursion zu beheben, nutze ich oft Caching. Pythons lru_cache speichert schon berechnete Werte, damit die Funktion die Arbeit nicht nochmal machen muss.
So mache ich das:
from functools import lru_cache
@lru_cache(maxsize = None)
def fib_cache(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib_cache(n-1) + fib_cache(n-2)
print(f"The Fibonacci Number is {fib_cache(10)}")
# The Fibonacci Number is 55Dieser Ansatz verbindet die Klarheit der Rekursion mit der Effizienz des Cachings.
Fortgeschrittenere Methoden zur Umsetzung der Fibonacci-Folge in Python
Wenn du nach anderen Möglichkeiten suchst, Fibonacci-Zahlen zu berechnen, findest du hier ein paar fortgeschrittenere Techniken:
Matrixpotenzierung
Matrixpotenzierung ist eine der besten Methoden, um Fibonacci-Zahlen für große Werte von n zu berechnen. Anstatt die Terme immer wieder neu zu berechnen, nutzt diese Methode die Matrixmultiplikation, um Ergebnisse in logarithmischer Zeit zu bekommen.
So hab ich das in Python gemacht:
import numpy as np
def fibonacci_matrix(n):
def matrix_power(matrix, power):
return np.linalg.matrix_power(matrix, power)
if n == 0:
return 0
matrix = np.array([[1, 1], [1, 0]])
result = matrix_power(matrix, n-1)
return result[0][0]
fibonacci_numbers = []
for i in range(10):
fibonacci_numbers.append(str(fibonacci_matrix(i)))
print(' '.join(fibonacci_numbers))
# 0 1 1 2 3 5 8 13 21 34In diesem Code wird, wenn n gleich 0 ist , 0 als Basisfall zurückgegeben. Für andere Werte wird die Matrix mit der Funktion matrix_power von numpy zur Potenz (n-1) erhoben. Die Fibonacci-Zahl an der Stelle n ist im Element oben links in der resultierenden Matrix zu finden.
Binet-Formel
Die Formel von Binet berechnet direkt die Fibonacci-Zahl nth ohne Iteration oder Rekursion. Es basiert auf dem Goldenen Schnitt, φ, und nutzt einen mathematischen Ausdruck, um das Ergebnis sofort zu berechnen.
Die Formel lautet:
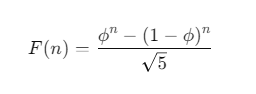
Wo:
- φ = (1 + √5) / 2Der Goldene Schnitt.
- 1 - φ ist die Konjugierte von φ.
Hier ist der Python-Code für die Binetsche Formel:
import math
def fibonacci_binet(n):
phi = (1 + math.sqrt(5)) / 2
return round((phi ** n - (1 - phi) ** n) / math.sqrt(5))
# Find the 10th Fibonacci number
n = 10
result = fibonacci_binet(n)
print(f"The Fibonacci Number of {n}th term is {result}" )
# The Fibonacci Number of 10th term is 55In diesem Code berechnet die Funktion fibonacci_binet(n) die Fibonacci-Zahl nth mit der Binetschen Formel. In der Funktion berechne ich phi (den Goldenen Schnitt) als (1 + math.sqrt(5)) / 2 und benutze math.sqrt() für die Quadratwurzel von 5. Dann wird die Formel (phi ** n - (1 - phi) ** n) / math.sqrt(5) benutzt, um die nth Fibonacci-Zahl direkt zu finden. Dann nehme ich die Funktion round(), um kleine Ungenauigkeiten bei Fließkommazahlen zu beheben.
Arrays
Du kannst sogar Arrays verwenden, um die ganze Fibonacci-Folge zu erzeugen und zu speichern. Das ist praktisch, wenn du mehrere Begriffe gleichzeitig brauchst.
Hier ist der Code dafür:
def fibonacci(n):
if n <= 0:
return "Incorrect Output"
data = [0, 1] # Initialize list with first two Fibonacci terms: 0 and 1
if n > 2:
for i in range(2, n): # Start loop from the third term
data.append(data[i-1] + data[i-2]) # Calculate next term as sum of previous two
return data[n-1] # Return the nth term
print(f"Fibonacci Number: {fibonacci(10)}")
# Fibonacci Number: 34Zurückverfolgung
Backtracking ist eine andere Möglichkeit, die ich nutzen könnte, vor allem wenn ich Rekursion mit Memoisierung kombinieren will, um die Leistung zu verbessern.
Hier ist der Code dafür:
def fibonacci_backtracking(n, computed ={0: 0, 1: 1}):
if n in computed:
return computed[n]
computed[n] = fibonacci_backtracking(n - 1) + fibonacci_backtracking(n - 2)
return computed[n]
n = 10
result = fibonacci_backtracking(n)
print(f"The {n}th Fibonacci term is {result}")
# The 10th Fibonacci term is 55Komplexität von Fibonacci-Algorithmen in Python
Wir haben jetzt schon ein paar Beispiele durch! Schauen wir uns jetzt mal die Unterschiede in Sachen Zeit- und Raumkomplexität an. Wie schon gesagt, sind manche Methoden von schnell, brauchen aber mehr Speicherplatz, während andere langsamer sind, dafür aber weniger Speicherplatz brauchen. Ich hab diese Tabelle gemacht, um zu sehen, wie gut die einzelnen Ansätze funktionieren.
| Methode | Zeitkomplexität | Raumkomplexität |
|---|---|---|
| Iterativ (For-Schleife) | O(n) | O(1) |
| Iterativ (While-Schleife) | O(n) | O(1) |
| Einfache Rekursion | O(2ⁿ) | O(n) |
| Memoization/Caching | O(n) | O(n) |
| Array-basiert | O(n) | O(n) |
| Rückverfolgungsmethode | O(2ⁿ) | O(2ⁿ) |
| Matrixpotenzierung | O(log n) | O(log n) |
In der Tabelle oben bedeutet die jeweilige Zeit- und Raumkomplexität Folgendes:
-
O(n): Der Algorithmus geht die Sequenz einmal durch, indem er für jedes Element eine feste Anzahl von Operationen macht. Die Zeit, die es braucht, steigt linear mit der Eingabegröße
n. -
O(1): Die Fibonacci-Zahl wird mit einer festen Anzahl von Schritten ohne Wiederholungen oder Rückgriffe berechnet.
-
O(2n):
nDer Algorithmus macht zwei rekursive Aufrufe für jede Eingabe, was dazu führt, dass die Anzahl der Funktionsaufrufe mit steigender Eingabe exponentiell wächst. -
O(log n): Die Laufzeit wächst proportional zum Logarithmus der Eingabegröße
n.
-
O(n): Der Algorithmus braucht Speicherplatz, der direkt mit der Anzahl der Eingaben wächst
n. Hier braucht jedes Element einen festen Platz. -
O(1): Der Speicherverbrauch bleibt unabhängig von der Eingabegröße gleich.
-
O(2n): Es braucht exponentiell viel Speicherplatz, weil für jeden Zweig neue Zustände erstellt werden.
-
O(log n): Zwischenmatrixmultiplikationen nutzen logarithmischen Speicher.
Abschließende Gedanken
Wie du gesehen hast, kannst du in Python Fibonacci-Zahlen mit vielen verschiedenen Methoden berechnen, von einfachen Schleifen bis hin zu fortgeschrittenen Techniken wie Matrixpotenzierung und der Binetschen Formel. Jede Methode hat ihre Vorteile und Nachteile.
Ich hoffe, du hast was über die Fibonacci-Folge und auch über Python-Programmierung gelernt. Wenn du mehr über Python und verwandte Themen erfahren möchtest, schau dir unseren Kurs Einführung in Python an. Du kannst auch unseren kompletten Lernpfad zum Python-Entwickler ausprobieren, Programmiertechniken lernen und sogar mit der Entwicklung deiner eigenen Pakete anfangen!
