Introducción a las funciones de activación en las redes neuronales

¿Qué son las funciones de activación?

Las funciones de activación son un componente integral de las redes neuronales que les permite aprender patrones complejos en los datos. Transforman la señal de entrada de un nodo de una red neuronal en una señal de salida que pasa a la capa siguiente. Sin funciones de activación, las redes neuronales se limitarían a modelar únicamente relaciones lineales entre entradas y salidas.

Las funciones de activación introducen no linealidades, lo que permite a las redes neuronales aprender mapeos muy complejos entre entradas y salidas.

Elegir la función de activación adecuada es crucial para entrenar redes neuronales que generalicen bien y proporcionen previsiones precisas. En este post, daremos una visión general de las funciones de activación más comunes, sus papeles y cómo seleccionar las funciones de activación adecuadas para diferentes casos de uso.

Tanto si te estás iniciando en el aprendizaje profundo como si eres un profesional experimentado, comprender a fondo las funciones de activación desarrollará tu intuición y mejorará tu aplicación de las redes neuronales.

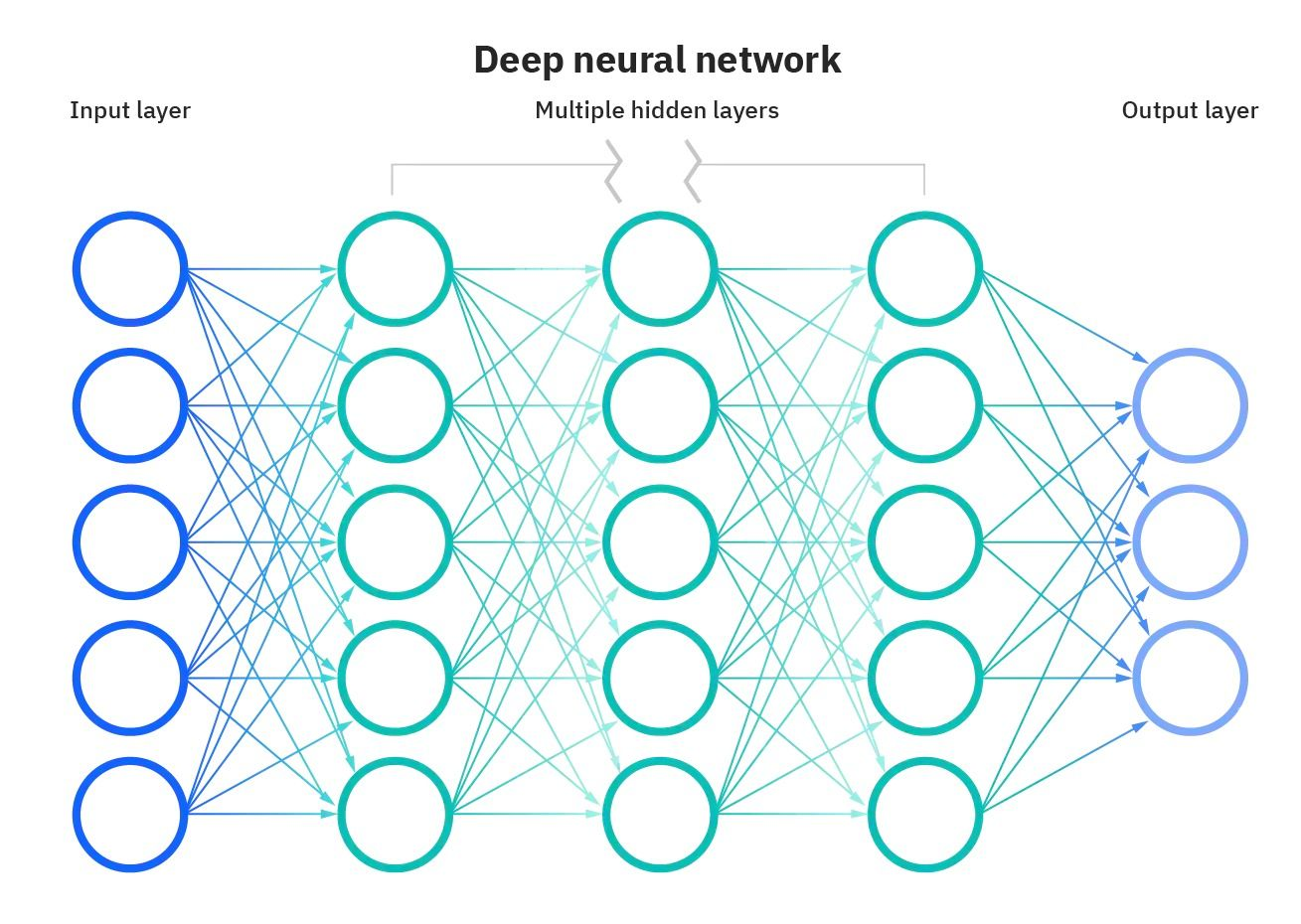
Fuente de la imagen de representación de red neuronal

¿Por qué son esenciales las funciones de activación?

Sin funciones de activación, las redes neuronales solo consistirían en operaciones lineales como la multiplicación de matrices. Todas las capas realizarían transformaciones lineales de la entrada, y no se introducirían no linealidades.

La mayoría de los datos del mundo real son no lineales. Por ejemplo, las relaciones entre los precios de la vivienda y el tamaño, los ingresos y las compras, etc., son no lineales. Si las redes neuronales no tuvieran funciones de activación, no podrían aprender los complejos patrones no lineales que existen en los datos del mundo real.

Las funciones de activación permiten a las redes neuronales aprender estas relaciones no lineales introduciendo comportamientos no lineales mediante funciones de activación. Esto aumenta enormemente la flexibilidad y la potencia de las redes neuronales para modelar datos complejos y matizados.

Tipos de funciones de activación

Las redes neuronales aprovechan diferentes tipos de funciones de activación para introducir no linealidades y permitir el aprendizaje de patrones complejos. Cada función de activación tiene sus propias propiedades y es adecuada para determinados casos de uso.

Por ejemplo, la función sigmoide es ideal para los problemas de clasificación binaria, softmax es útil para la previsión multiclase y ReLU ayuda a superar el problema de desvanecimiento de gradiente.

Utilizar la función de activación adecuada para la tarea conduce a un entrenamiento más rápido y a un mejor rendimiento.

Veamos algunas de las funciones de activación comunes:

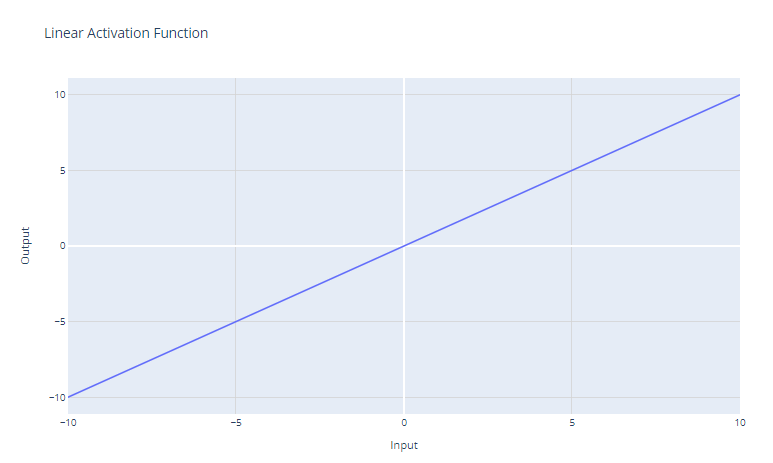
La función de activación lineal es la función de activación más sencilla, definida como:

f(x) = x

Simplemente devuelve la entrada x como salida. Gráficamente, es una línea recta con una pendiente de 1.

El principal caso de uso de la función de activación lineal es en la capa de salida de una red neuronal utilizada para la regresión. Para los problemas de regresión en los que queremos prever un valor numérico, utilizar una función de activación lineal en la capa de salida garantiza que la red neuronal produzca un valor numérico. La función de activación lineal no reduce ni transforma la salida, por lo que se devuelve el valor real previsto.

Sin embargo, la función de activación lineal rara vez se utiliza en las capas ocultas de las redes neuronales. Esto se debe a que no proporciona ninguna no linealidad. El objetivo de las capas ocultas es aprender combinaciones no lineales de las características de entrada. Utilizar una activación lineal todo el tiempo restringiría el modelo a aprender solo transformaciones lineales de la entrada.

Activación sigmoide

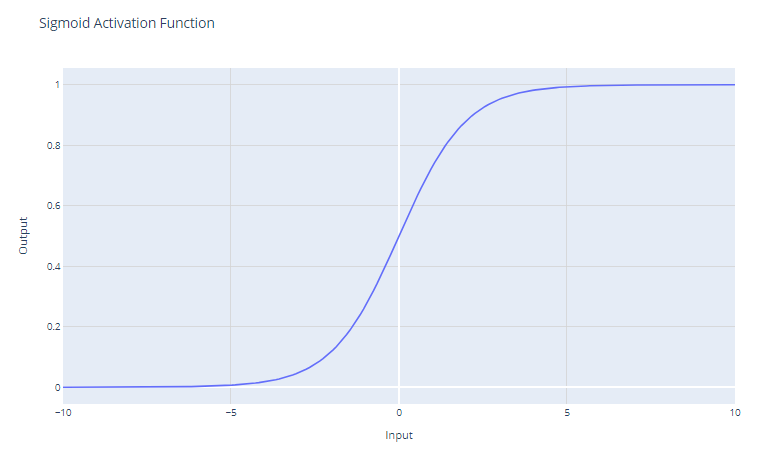
La función de activación sigmoide, a menudo representada como σ(x), es una función infinitamente diferenciable históricamente importante en el desarrollo de las redes neuronales. La función de activación sigmoide tiene la forma matemática:

f(x) = 1/(1 + e^-x)

Toma una entrada de valor real y la reduce a un valor entre 0 y 1. La función sigmoide tiene una curva en forma de "S" que tiende a 0 para los números negativos grandes y a 1 para los números positivos grandes. Los resultados pueden interpretarse fácilmente como probabilidades, lo que la hace natural para los problemas de clasificación binaria.

Las unidades sigmoides fueron populares en las primeras redes neuronales, ya que el gradiente es más fuerte cuando la salida de la unidad está cerca de 0,5, lo que permite un entrenamiento eficaz por retropropagación. Sin embargo, las unidades sigmoides sufren el problema de "desvanecimiento de gradiente", que dificulta el aprendizaje en las redes neuronales profundas.

A medida que los valores de entrada se vuelven significativamente positivos o negativos, la función se satura en 0 o 1, con una pendiente extremadamente plana. En estas regiones, el gradiente es muy próximo a cero. Esto da lugar a cambios muy pequeños en los pesos durante la retropropagación, sobre todo para las neuronas de las primeras capas de las redes profundas, lo que hace que el aprendizaje sea penosamente lento o incluso lo detenga. Esto se conoce como el problema de desvanecimiento de gradiente en las redes neuronales.

El principal caso de uso de la función sigmoide es como activación de la capa de salida de los modelos de clasificación binaria. Reduce la salida a un valor de probabilidad entre 0 y 1, que puede interpretarse como la probabilidad de que la entrada pertenezca a una clase determinada.

Activación de tangente hiperbólica (tanh)

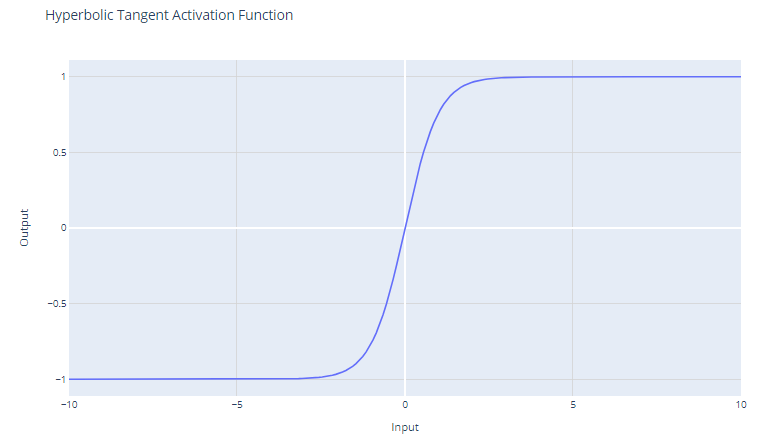
La función de activación de tangente hiperbólica (tanh) se define como:

f(x) = (e^x - e^ - x)/(e^x + e^ - x)

La función tanh produce valores en el intervalo de -1 a +1. Esto significa que puede tratar valores negativos con más eficacia que la función sigmoide, que tiene un intervalo de 0 a 1.

A diferencia de la función sigmoide, tanh está centrada en cero, lo que significa que su resultado es simétrico alrededor del origen del sistema de coordenadas. Esto suele considerarse una ventaja porque puede ayudar a que el algoritmo de aprendizaje converja más rápidamente.

Como el resultado de tanh oscila entre -1 y +1, tiene gradientes más fuertes que la función sigmoide. Los gradientes más fuertes suelen dar lugar a un aprendizaje y una convergencia más rápidos durante el entrenamiento, porque tienden a ser más resistentes frente al problema de desvanecimiento de gradiente que los gradientes de la función sigmoide.

A pesar de estas ventajas, la función tanh sigue sufriendo el problema de desvanecimiento de gradiente. Durante la retropropagación, los gradientes de la función tanh pueden llegar a ser muy pequeños (próximos a cero). Esta cuestión es especialmente problemática para las redes profundas con muchas capas; los gradientes de la función de pérdida pueden llegar a ser demasiado pequeños para realizar cambios significativos en los pesos durante el entrenamiento, ya que se retropropagan a las capas iniciales. Esto puede ralentizar drásticamente el proceso de entrenamiento y provocar malas propiedades de convergencia.

La función tanh se utiliza con frecuencia en las capas ocultas de una red neuronal. Debido a su naturaleza centrada en cero, cuando los datos también se normalizan para que tengan media cero, puede resultar un entrenamiento más eficiente.

Si hay que elegir entre la función sigmoide y la función tanh y no se tiene ninguna razón específica para preferir una a la otra, tanh suele ser la mejor opción por las razones antes mencionadas. Sin embargo, la decisión también puede verse influida por el caso de uso concreto y el comportamiento de la red durante los experimentos de entrenamiento iniciales.

Puedes construir una red neuronal sencilla desde cero utilizando PyTorch siguiendo nuestro tutorial de Kurtis Pykes o, si eres un usuario avanzado, nuestro curso de aprendizaje profundo con PyTorch es para ti.

Activación de unidad lineal rectificada (ReLU)

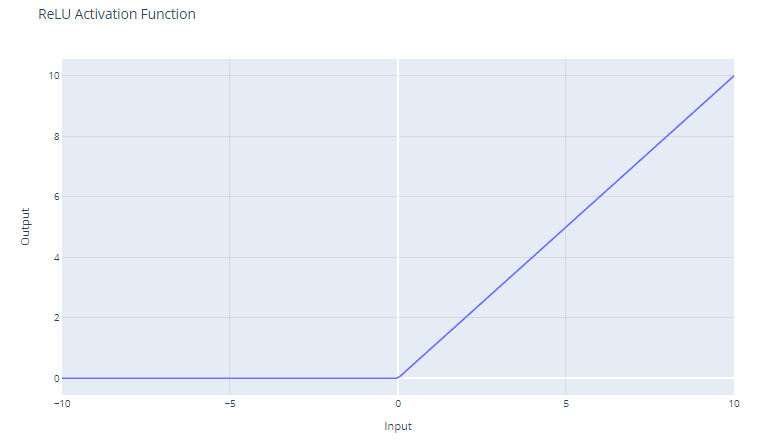
La función de activación de unidad lineal rectificada (ReLU) tiene la forma:

f(x) = max(0, x)

Umbraliza la entrada en cero, devolviendo 0 para valores negativos y la propia entrada para valores positivos.

Para entradas mayores que 0, ReLU actúa como una función lineal con un gradiente de 1. Esto significa que no modifica la escala de las entradas positivas y permite que el gradiente pase sin cambios durante la retropropagación. Esta propiedad es fundamental para mitigar el problema de desvanecimiento de gradiente.

Aunque ReLU es lineal para la mitad de su espacio de entrada, técnicamente es una función no lineal porque tiene un punto no diferenciable en x=0, donde cambia bruscamente con respecto a x. Esta no linealidad permite a las redes neuronales aprender patrones complejos

Como ReLU produce cero para todas las entradas negativas, conduce naturalmente a activaciones dispersas; en cualquier momento, solo se activa un subconjunto de neuronas, lo que conduce a una computación más eficiente.

La función ReLU es computacionalmente poco costosa porque implica un simple umbral en cero. Esto permite a las redes escalar a muchas capas sin un aumento significativo de la carga computacional, en comparación con funciones más complejas como la función tanh o la sigmoide.

Activación softmax

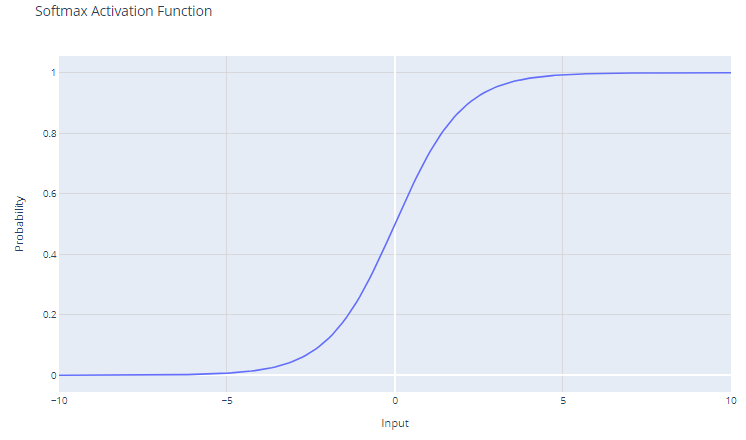
La función de activación softmax, también conocida como función exponencial normalizada, es especialmente útil en el contexto de los problemas de clasificación multiclase. Esta función opera sobre un vector, a menudo denominado logits, que representa las previsiones o las puntuaciones brutas de cada clase calculadas por las capas anteriores de una red neuronal.

Para un vector de entrada x con elementos x1, x2, ..., xC, la función softmax se define como:

f(xi) = e^xi/Σj e^xj

El resultado de la función softmax es una distribución de probabilidad cuya suma es uno. Cada elemento del resultado representa la probabilidad de que la entrada pertenezca a una clase determinada.

El uso de la función exponencial garantiza que todos los valores de salida sean no negativos. Esto es crucial porque las probabilidades no pueden ser negativas.

Softmax amplifica las diferencias en el vector de entrada. Incluso pequeñas diferencias en los valores de entrada pueden dar lugar a diferencias sustanciales en las probabilidades de salida, con los valores de entrada más altos tendiendo a dominar en la distribución de probabilidad resultante.

Softmax se suele utilizar en la capa de salida de una red neuronal cuando la tarea consiste en clasificar una entrada en una de varias (más de dos) categorías posibles (clasificación multiclase).

Las probabilidades producidas por la función softmax pueden interpretarse como puntuaciones de confianza para cada clase, lo que proporciona información sobre la certeza del modelo en cuanto a sus previsiones.

Como softmax amplifica las diferencias, puede ser sensible a los valores atípicos o extremos. Por ejemplo, si el vector de entrada tiene un valor muy grande, softmax puede "reducir" las probabilidades de otras clases, dando lugar a un modelo demasiado confiado.

Elección de la función de activación adecuada

La elección de la función de activación depende del tipo de problema que intentes resolver. Aquí tienes algunas pautas:

Para la clasificación binaria:

Utiliza la función de activación sigmoide en la capa de salida. Reducirá las salidas a un valor entre 0 y 1, que representa las probabilidades de las dos clases.

Para la clasificación multiclase:

Utiliza la función de activación softmax en la capa de salida. Dará como resultado distribuciones de probabilidad sobre todas las clases.

Si no estás seguro:

Utiliza la función de activación ReLU en las capas ocultas. ReLU es la función de activación predeterminada más común y suele ser una buena elección.

Conclusión

Hemos explorado el papel fundamental que desempeñan las funciones de activación en el entrenamiento de las redes neuronales. Hemos visto que no son meros extras opcionales, sino elementos esenciales que permiten a las redes neuronales captar y modelar la complejidad inherente a los datos del mundo real. Desde la sencilla pero eficaz ReLU hasta las interpretaciones probabilísticas que proporciona la función softmax, cada función de activación tiene su lugar y su propósito dentro de las distintas capas de una red y en diversos dominios de problemas.

A medida que las redes neuronales sigan evolucionando, la exploración de las funciones de activación se ampliará sin duda, e incluirá posiblemente nuevas formas que aborden retos específicos de las arquitecturas emergentes. Sin embargo, es probable que los principios y funciones tratados en este blog sigan siendo el núcleo del diseño de redes neuronales en un futuro próximo.

La selección cuidadosa de las funciones de activación es un acto de equilibrio (una mezcla de comprensión científica e intuición ingeniosa) que puede afectar significativamente al rendimiento de las redes neuronales.

¿Estás interesado en el aprendizaje profundo con el marco Keras? Consulta nuestro curso Introducción al aprendizaje profundo con Keras.