Curso
En este tutorial, verá cómo puede utilizar un modelo de series temporales conocido como Memoria a Largo Plazo. Los modelos LSTM son potentes, especialmente para retener una memoria a largo plazo, por diseño, como verás más adelante. En este tutorial abordará los siguientes temas:
- Comprenda por qué tendría que ser capaz de predecir los movimientos de las cotizaciones bursátiles;
- Descargue los datos - Utilizará datos bursátiles recopilados de Yahoo Finanzas;
- Dividir los datos de entrenamiento-prueba y también realizar alguna normalización de los datos;
- Repase y aplique algunas técnicas de promediación que pueden utilizarse para realizar predicciones con un paso de antelación;
- Motivar y discutir brevemente un modelo LSTM ya que permite predecir más de un paso por delante;
- Predecir y visualizar el futuro mercado bursátil con datos actuales
Si no estás familiarizado con el aprendizaje profundo o las redes neuronales, deberías echar un vistazo a nuestro curso Aprendizaje profundo en Python. Cubre los conceptos básicos, así como la forma de construir una red neuronal por su cuenta en Keras. Se trata de un paquete diferente a TensorFlow, que se utilizará en este tutorial, pero la idea es la misma.
¿Por qué se necesitan modelos de series temporales?
Le gustaría modelizar correctamente los precios de las acciones para que, como comprador de acciones, pueda decidir razonablemente cuándo comprarlas y cuándo venderlas para obtener beneficios. Aquí es donde entra en juego la modelización de series temporales. Se necesitan buenos modelos de aprendizaje automático que puedan observar el historial de una secuencia de datos y predecir correctamente cuáles van a ser los elementos futuros de la secuencia.
Advertencia: Las cotizaciones bursátiles son muy imprevisibles y volátiles. Esto significa que no existen patrones coherentes en los datos que permitan modelizar los precios de las acciones a lo largo del tiempo de forma casi perfecta. No lo tome de mí, tómelo del economista de la Universidad de Princeton Burton Malkiel, que argumenta en su libro de 1973, "A Random Walk Down Wall Street", que si el mercado es realmente eficiente y el precio de una acción refleja todos los factores inmediatamente en cuanto se hacen públicos, un mono con los ojos vendados lanzando dardos a una lista de acciones de un periódico debería hacerlo tan bien como cualquier profesional de la inversión.
Sin embargo, no vayamos hasta el final creyendo que se trata sólo de un proceso estocástico o aleatorio y que no hay esperanza para el aprendizaje automático. Veamos si al menos puedes modelar los datos, de modo que las predicciones que hagas se correlacionen con el comportamiento real de los datos. En otras palabras, no necesita los valores exactos de las acciones en el futuro, sino los movimientos del precio de las acciones (es decir, si van a subir o bajar en un futuro próximo).
# Make sure that you have all these libaries available to run the code successfully
from pandas_datareader import data
import matplotlib.pyplot as plt
import pandas as pd
import datetime as dt
import urllib.request, json
import os
import numpy as np
import tensorflow as tf # This code has been tested with TensorFlow 1.6
from sklearn.preprocessing import MinMaxScalerDescargar los datos
Utilizará datos de las siguientes fuentes:
-
Alpha Vantage Stock API. Antes de empezar, sin embargo, necesitará una clave API, que puede obtener gratuitamente aquí. Después, puedes asignar esa tecla a la variable
api_key. En este tutorial, recuperaremos 20 años de datos históricos de las acciones de American Airlines. Como lectura opcional, puede consultar esta guía de iniciación a la API de valores para conocer las mejores prácticas de trabajo con datos históricos del mercado. -
Utiliza los datos de esta página. Deberá copiar la carpeta Stocks del archivo zip en la carpeta de inicio de su proyecto.
Las cotizaciones bursátiles son muy variadas. Lo son,
- Abierto: Cotización de apertura del día
- Cerrar: Cotización de cierre del día
- Alta: Cotización más alta de los datos
- Bajo: Cotización más baja del día
Obtener datos de Alphavantage
Primero cargará los datos de Alpha Vantage. Como va a utilizar los precios de la bolsa de American Airlines para hacer sus predicciones, ponga el ticker en "AAL". Además, también se define un url_string, que devolverá un archivo JSON con todos los datos bursátiles de American Airlines de los últimos 20 años, y un file_to_save, que será el archivo en el que se guardarán los datos. Utilizarás la variable ticker que definiste anteriormente para ayudar a nombrar este archivo.
A continuación, vas a especificar una condición: si aún no has guardado los datos, seguirás adelante y tomarás los datos de la URL que estableciste en url_string; Almacenarás los valores de fecha, bajo, alto, volumen, cierre, apertura en un pandas DataFrame df y lo guardarás en file_to_save. Sin embargo, si los datos ya están ahí, bastará con cargarlos desde el CSV.
Obtener datos de Kaggle
Los datos encontrados en Kaggle son una colección de archivos csv y no tienes que hacer ningún preprocesamiento, por lo que puedes cargar directamente los datos en un Pandas DataFrame.
data_source = 'kaggle' # alphavantage or kaggle
if data_source == 'alphavantage':
# ====================== Loading Data from Alpha Vantage ==================================
api_key = '<your API key>'
# American Airlines stock market prices
ticker = "AAL"
# JSON file with all the stock market data for AAL from the last 20 years
url_string = "https://www.alphavantage.co/query?function=TIME_SERIES_DAILY&symbol=%s&outputsize=full&apikey=%s"%(ticker,api_key)
# Save data to this file
file_to_save = 'stock_market_data-%s.csv'%ticker
# If you haven't already saved data,
# Go ahead and grab the data from the url
# And store date, low, high, volume, close, open values to a Pandas DataFrame
if not os.path.exists(file_to_save):
with urllib.request.urlopen(url_string) as url:
data = json.loads(url.read().decode())
# extract stock market data
data = data['Time Series (Daily)']
df = pd.DataFrame(columns=['Date','Low','High','Close','Open'])
for k,v in data.items():
date = dt.datetime.strptime(k, '%Y-%m-%d')
data_row = [date.date(),float(v['3. low']),float(v['2. high']),
float(v['4. close']),float(v['1. open'])]
df.loc[-1,:] = data_row
df.index = df.index + 1
print('Data saved to : %s'%file_to_save)
df.to_csv(file_to_save)
# If the data is already there, just load it from the CSV
else:
print('File already exists. Loading data from CSV')
df = pd.read_csv(file_to_save)
else:
# ====================== Loading Data from Kaggle ==================================
# You will be using HP's data. Feel free to experiment with other data.
# But while doing so, be careful to have a large enough dataset and also pay attention to the data normalization
df = pd.read_csv(os.path.join('Stocks','hpq.us.txt'),delimiter=',',usecols=['Date','Open','High','Low','Close'])
print('Loaded data from the Kaggle repository')
Data saved to : stock_market_data-AAL.csv
Exploración de datos
Aquí imprimirá los datos recogidos en el DataFrame. También debe asegurarse de que los datos están ordenados por fecha, ya que el orden de los datos es crucial en la modelización de series temporales.
# Sort DataFrame by date
df = df.sort_values('Date')
# Double check the result
df.head()
| Fecha | Abrir | Alta | Bajo | Cerrar | |
|---|---|---|---|---|---|
| 0 | 1970-01-02 | 0.30627 | 0.30627 | 0.30627 | 0.30627 |
| 1 | 1970-01-05 | 0.30627 | 0.31768 | 0.30627 | 0.31385 |
| 2 | 1970-01-06 | 0.31385 | 0.31385 | 0.30996 | 0.30996 |
| 3 | 1970-01-07 | 0.31385 | 0.31385 | 0.31385 | 0.31385 |
| 4 | 1970-01-08 | 0.31385 | 0.31768 | 0.31385 | 0.31385 |
Visualización de datos
Ahora veamos qué tipo de datos tienes. Quiere datos con varios patrones que se produzcan a lo largo del tiempo.
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),(df['Low']+df['High'])/2.0)
plt.xticks(range(0,df.shape[0],500),df['Date'].loc[::500],rotation=45)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.show()
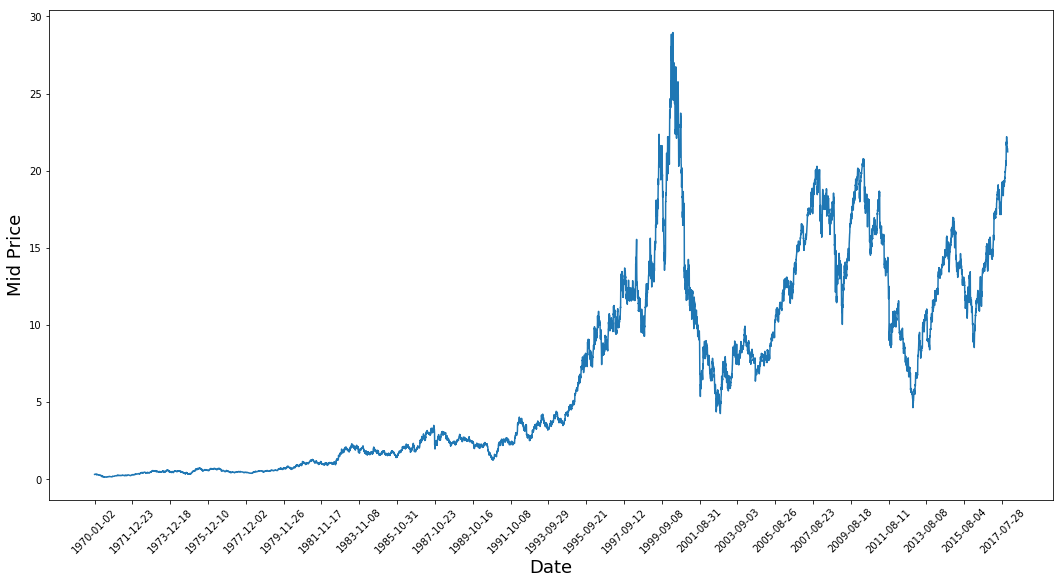
Este gráfico ya dice muchas cosas. La razón específica por la que elegí esta empresa en lugar de otras es que este gráfico está repleto de diferentes comportamientos de los precios de las acciones a lo largo del tiempo. De este modo, el aprendizaje será más sólido y podrá comprobar la calidad de las predicciones en distintas situaciones.
Otra cosa que hay que observar es que los valores cercanos a 2017 son mucho más altos y fluctúan más que los valores cercanos a la década de 1970. Por lo tanto, debe asegurarse de que los datos se comportan en rangos de valores similares a lo largo de todo el periodo de tiempo. De ello se encargará durante la fase de normalización de los datos.
Dividir los datos en un conjunto de entrenamiento y un conjunto de prueba
Utilizará el precio medio calculado tomando la media de los precios más altos y más bajos registrados en un día.
# First calculate the mid prices from the highest and lowest
high_prices = df.loc[:,'High'].as_matrix()
low_prices = df.loc[:,'Low'].as_matrix()
mid_prices = (high_prices+low_prices)/2.0
Ahora puede dividir los datos de entrenamiento y los datos de prueba. Los datos de entrenamiento serán los primeros 11.000 puntos de datos de la serie temporal y el resto serán datos de prueba.
train_data = mid_prices[:11000]
test_data = mid_prices[11000:]
Normalización de los datos
Ahora necesita definir un escalador para normalizar los datos. MinMaxScalar escala todos los datos para que estén en la región de 0 y 1. También puede remodelar los datos de entrenamiento y de prueba para que tengan la forma [data_size, num_features].
# Scale the data to be between 0 and 1
# When scaling remember! You normalize both test and train data with respect to training data
# Because you are not supposed to have access to test data
scaler = MinMaxScaler()
train_data = train_data.reshape(-1,1)
test_data = test_data.reshape(-1,1)
Debido a la observación que hizo anteriormente, es decir, que los distintos periodos de tiempo de los datos tienen distintos rangos de valores, normaliza los datos dividiendo la serie completa en ventanas. Si no lo hace, los datos anteriores serán cercanos a 0 y no aportarán mucho valor al proceso de aprendizaje. Aquí se elige un tamaño de ventana de 2500.
Consejo: cuando elija el tamaño de la ventana, asegúrese de que no es demasiado pequeño, ya que cuando se realiza la normalización por ventanas, puede introducirse una interrupción al final de cada ventana, ya que cada ventana se normaliza de forma independiente.
En este ejemplo, 4 puntos de datos se verán afectados por esto. Pero dado que tienes 11.000 puntos de datos, 4 puntos no causarán ningún problema.
# Train the Scaler with training data and smooth data
smoothing_window_size = 2500
for di in range(0,10000,smoothing_window_size):
scaler.fit(train_data[di:di+smoothing_window_size,:])
train_data[di:di+smoothing_window_size,:] = scaler.transform(train_data[di:di+smoothing_window_size,:])
# You normalize the last bit of remaining data
scaler.fit(train_data[di+smoothing_window_size:,:])
train_data[di+smoothing_window_size:,:] = scaler.transform(train_data[di+smoothing_window_size:,:])
Devolver a los datos la forma de [data_size]
# Reshape both train and test data
train_data = train_data.reshape(-1)
# Normalize test data
test_data = scaler.transform(test_data).reshape(-1)
Ahora puede suavizar los datos utilizando la media móvil exponencial. De este modo, se elimina la irregularidad inherente a los datos de las cotizaciones bursátiles y se obtiene una curva más suave.
Tenga en cuenta que sólo debe suavizar los datos de entrenamiento.
# Now perform exponential moving average smoothing
# So the data will have a smoother curve than the original ragged data
EMA = 0.0
gamma = 0.1
for ti in range(11000):
EMA = gamma*train_data[ti] + (1-gamma)*EMA
train_data[ti] = EMA
# Used for visualization and test purposes
all_mid_data = np.concatenate([train_data,test_data],axis=0)
Predicción anticipada mediante promediado
Los mecanismos de promediación permiten predecir (a menudo con un paso de tiempo de antelación) representando el precio futuro de las acciones como una media de los precios de las acciones observados anteriormente. Hacer esto para más de un paso temporal puede producir resultados bastante malos. A continuación veremos dos técnicas de promediación: la media estándar y la media móvil exponencial. Evaluará cualitativa (inspección visual) y cuantitativamente (error cuadrático medio) los resultados producidos por los dos algoritmos.
El Error Cuadrático Medio (ECM) puede calcularse tomando el Error Cuadrático entre el valor real en un paso adelante y el valor predicho y promediándolo sobre todas las predicciones.
Media estándar
Se puede entender la dificultad de este problema intentando primero modelarlo como un problema de cálculo medio. En primer lugar, intentará predecir las cotizaciones bursátiles futuras (por ejemplo, xt+1 ) como media de las cotizaciones bursátiles observadas anteriormente dentro de una ventana de tamaño fijo (por ejemplo, xt-N, ..., xt) (digamos, los 100 días anteriores). A continuación, probará con un método un poco más sofisticado de "media móvil exponencial" y verá lo bien que funciona. A continuación, pasará al "santo grial" de la predicción de series temporales: los modelos de memoria a largo plazo.
Primero verás cómo funciona la media normal. Eso es lo que tú dices,
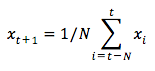
En otras palabras, se dice que la predicción a $t+1$ es el valor medio de todos los precios de las acciones observados dentro de una ventana de $t$ a $t-N$.
window_size = 100
N = train_data.size
std_avg_predictions = []
std_avg_x = []
mse_errors = []
for pred_idx in range(window_size,N):
if pred_idx >= N:
date = dt.datetime.strptime(k, '%Y-%m-%d').date() + dt.timedelta(days=1)
else:
date = df.loc[pred_idx,'Date']
std_avg_predictions.append(np.mean(train_data[pred_idx-window_size:pred_idx]))
mse_errors.append((std_avg_predictions[-1]-train_data[pred_idx])**2)
std_avg_x.append(date)
print('MSE error for standard averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for standard averaging: 0.00418
Eche un vistazo a los resultados promediados a continuación. Sigue bastante de cerca el comportamiento real de las acciones. A continuación, se estudiará un método de predicción más preciso de un solo paso.
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),all_mid_data,color='b',label='True')
plt.plot(range(window_size,N),std_avg_predictions,color='orange',label='Prediction')
#plt.xticks(range(0,df.shape[0],50),df['Date'].loc[::50],rotation=45)
plt.xlabel('Date')
plt.ylabel('Mid Price')
plt.legend(fontsize=18)
plt.show()
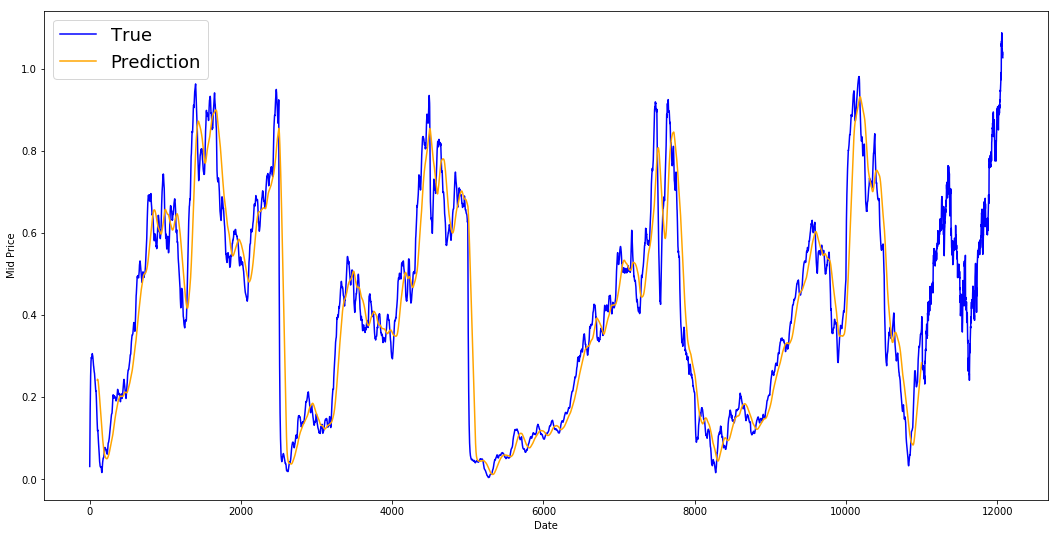
Entonces, ¿qué dicen los gráficos anteriores (y el MSE)?
Parece que no es un modelo demasiado malo para predicciones muy cortas (con un día de antelación). Dado que los precios de las acciones no cambian de 0 a 100 de la noche a la mañana, este comportamiento es sensato. A continuación, veremos una técnica de promediación más sofisticada conocida como media móvil exponencial.
Media móvil exponencial
Es posible que haya visto algunos artículos en Internet en los que se utilizan modelos muy complejos y se predice casi con exactitud el comportamiento del mercado bursátil. Pero, ¡cuidado! Son meras ilusiones ópticas y no se deben al aprendizaje de algo útil. A continuación verá cómo puede reproducir ese comportamiento con un sencillo método de promediación.
En el método de media móvil exponencial, se calcula $x_{t+1}$ como,
- $x\_{t+1} = EMA\_{t} = \gamma \times EMA_{t-1} + (1-\gamma) x_t$ donde $EMA_0 = 0$ y $EMA$ es el valor de la media móvil exponencial que mantiene en el tiempo.
La ecuación anterior básicamente calcula la media móvil exponencial de $t+1$ paso de tiempo y utiliza que como la predicción de un paso por delante. $\gamma$ decide cuál es la contribución de la predicción más reciente a la EMA. Por ejemplo, una $\gamma=0,1$ introduce sólo el 10% del valor actual en la EMA. Como sólo se toma una fracción muy pequeña de los más recientes, permite conservar valores mucho más antiguos que se vieron muy al principio de la media. Vea lo bien que se ve cuando se utiliza para predecir un paso por delante a continuación.
window_size = 100
N = train_data.size
run_avg_predictions = []
run_avg_x = []
mse_errors = []
running_mean = 0.0
run_avg_predictions.append(running_mean)
decay = 0.5
for pred_idx in range(1,N):
running_mean = running_mean*decay + (1.0-decay)*train_data[pred_idx-1]
run_avg_predictions.append(running_mean)
mse_errors.append((run_avg_predictions[-1]-train_data[pred_idx])**2)
run_avg_x.append(date)
print('MSE error for EMA averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for EMA averaging: 0.00003
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),all_mid_data,color='b',label='True')
plt.plot(range(0,N),run_avg_predictions,color='orange', label='Prediction')
#plt.xticks(range(0,df.shape[0],50),df['Date'].loc[::50],rotation=45)
plt.xlabel('Date')
plt.ylabel('Mid Price')
plt.legend(fontsize=18)
plt.show()
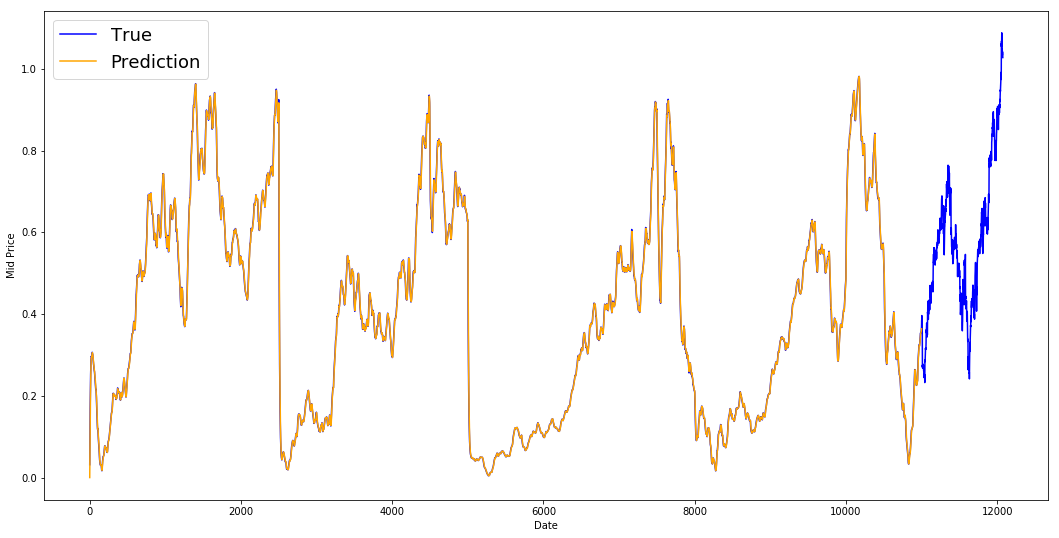
Si la media móvil exponencial es tan buena, ¿por qué se necesitan modelos mejores?
Se ve que se ajusta a una línea perfecta que sigue la distribución True (y se justifica por el muy bajo MSE). En la práctica, no se puede hacer mucho sólo con el valor bursátil del día siguiente. Personalmente, lo que me gustaría saber no es el precio exacto de la bolsa para el día siguiente, sino si los precios de la bolsa subirán o bajarán en los próximos 30 días. Intenta hacerlo y pondrás en evidencia la incapacidad del método EMA.
Ahora intentará hacer predicciones en ventanas (digamos que predice la ventana de los próximos 2 días, en lugar de sólo el día siguiente). Entonces te darás cuenta de lo mal que puede ir la EMA. He aquí un ejemplo:
Predecir más de un paso en el futuro
Para concretar, supongamos valores, digamos $x_t=0,4$, $EMA=0,5$ y $\gamma = 0,5$.
- Digamos que obtiene la salida con la siguiente ecuación
- Xt+1 = EMAt = γ × EMAt-1 + (1 - γ)Xt
- Por tanto, xt+1 = 0,5 × 0,5 + (1-0,5) × 0,4 = 0,45
- Por tanto, Xt+1 = EMAt = 0,45
- Así que la siguiente predicción Xt+2 se convierte en,
- Xt+2 = γ × EMAt + (1-γ)Xt+1
- Que es Xt+2 = γ × EMA_t + (1-γ) EMAt = EMAt
- O, en este ejemplo, Xt+2 = Xt+1 = 0,45
Así que no importa cuántos pasos predigas en el futuro, seguirás obteniendo la misma respuesta para todos los pasos de predicción futuros.
Una solución que le proporcionará información útil es recurrir a algoritmos basados en el impulso. Hacen predicciones basándose en si los valores recientes pasados estaban subiendo o bajando (no los valores exactos). Por ejemplo, dirán que es probable que el precio del día siguiente sea más bajo, si los precios han estado bajando durante los últimos días, lo que suena razonable. Sin embargo, utilizará un modelo más complejo: un modelo LSTM.
Estos modelos han irrumpido con fuerza en el ámbito de la predicción de series temporales, porque son muy buenos modelizando datos de series temporales. Verás si realmente hay patrones ocultos en los datos que puedas explotar.
Introducción a los LSTM: Predicción de movimientos bursátiles a largo plazo
Los modelos de memoria a corto plazo son modelos de series temporales extremadamente potentes. Pueden predecir un número arbitrario de pasos en el futuro. Un módulo (o célula) LSTM tiene 5 componentes esenciales que le permiten modelar datos tanto a largo como a corto plazo.
- Estado de la célula (ct) - Representa la memoria interna de la célula que almacena tanto la memoria a corto plazo como la memoria a largo plazo.
- Estado oculto (ht): es la información del estado de salida calculada en función de la entrada actual, el estado oculto anterior y la entrada de la celda actual, que finalmente se utiliza para predecir los precios futuros de la bolsa. Además, el estado oculto puede decidir recuperar sólo los tipos de memoria a corto o largo plazo, o ambos, almacenados en el estado celular para realizar la siguiente predicción.
- Puerta de entrada (it) - Decide cuánta información de la entrada actual fluye al estado de la célula.
- Puerta de olvido (ft) - Decide cuánta información de la entrada actual y del estado anterior de la célula fluye al estado actual de la célula.
- Puerta de salida (ot) - Decide cuánta información del estado actual de la célula fluye al estado oculto, de modo que si es necesario LSTM sólo puede recoger las memorias a largo plazo o las memorias a corto plazo y las memorias a largo plazo.
A continuación se muestra una célula.
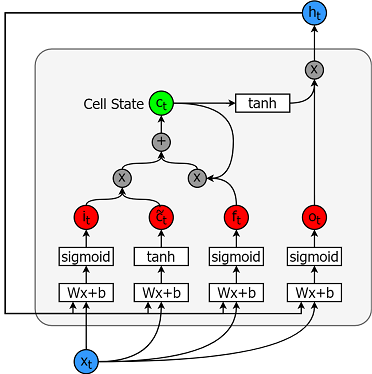
Y las ecuaciones para calcular cada una de estas entidades son las siguientes.
- it = σ(WixXt + Wihht-1 +bi)
- $\tilde{c}\_t = \sigma(W\_{cx}x\_t + W\_{ch}h_{t-1} + b_c)$
- $f\_t = \sigma(W\_{fx}x\_t + W\_{fh}h_{t-1}+b_f)$
- $c_t = f\_t c\_{t-1} + i_t \tilde{c}_t$
- $o\_t = \sigma(W\_{ox}x\_t + W\_{oh}h_{t-1}+b_o)$
- $h_t = o_t tanh(c_t)$
Para una mejor comprensión (más técnica) de los LSTM, puede consultar este artículo.
TensorFlow proporciona una buena sub API (llamada RNN API) para implementar modelos de series temporales. Lo utilizarás para tus implementaciones.
Generador de datos
Primero va a implementar un generador de datos para entrenar su modelo. Este generador de datos tendrá un método llamado .unroll_batches(...) que dará como salida un conjunto de lotes num_unrollings de datos de entrada obtenidos secuencialmente, donde un lote de datos es de tamaño [batch_size, 1]. Cada lote de datos de entrada tendrá su correspondiente lote de datos de salida.
Por ejemplo, si num_unrollings=3 y batch_size=4 un conjunto de lotes desenrollados podría tener este aspecto,
- datos de entrada: $[x_0,x_10,x_20,x_30], [x_1,x_11,x_21,x_31], [x_2,x_12,x_22,x_32]$
- datos de salida: $[x_1,x_11,x_21,x_31], [x_2,x_12,x_22,x_32], [x_3,x_13,x_23,x_33]$
Aumento de datos
También para hacer su modelo robusto que no hará que la salida para $x\_t$ siempre $x\_{t+1}$. En su lugar, muestreará aleatoriamente una salida del conjunto $x\_{t+1},x\_{t+2},\ldots,x_{t+N}$ donde $N$ es un tamaño de ventana pequeño.
Aquí estás haciendo la siguiente suposición:
- $x\_{t+1},x\_{t+2},\ldots,x_{t+N}$ no estarán muy lejos unos de otros
Personalmente, creo que es una hipótesis razonable para predecir el movimiento de las acciones.
A continuación se ilustra visualmente cómo se crea un lote de datos.
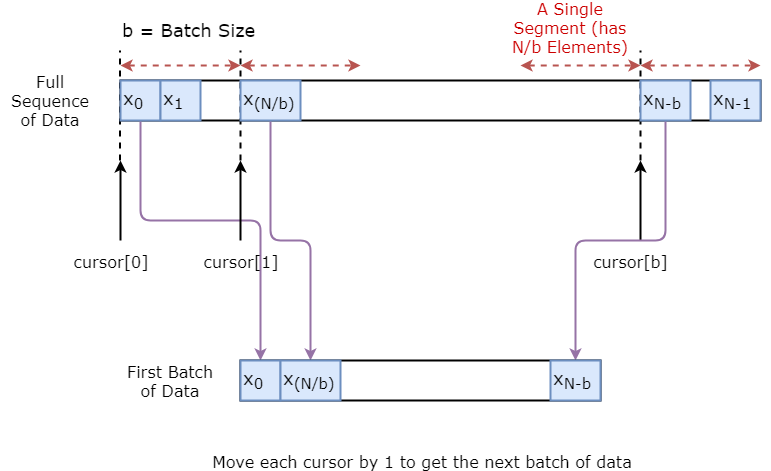
class DataGeneratorSeq(object):
def __init__(self,prices,batch_size,num_unroll):
self._prices = prices
self._prices_length = len(self._prices) - num_unroll
self._batch_size = batch_size
self._num_unroll = num_unroll
self._segments = self._prices_length //self._batch_size
self._cursor = [offset * self._segments for offset in range(self._batch_size)]
def next_batch(self):
batch_data = np.zeros((self._batch_size),dtype=np.float32)
batch_labels = np.zeros((self._batch_size),dtype=np.float32)
for b in range(self._batch_size):
if self._cursor[b]+1>=self._prices_length:
#self._cursor[b] = b * self._segments
self._cursor[b] = np.random.randint(0,(b+1)*self._segments)
batch_data[b] = self._prices[self._cursor[b]]
batch_labels[b]= self._prices[self._cursor[b]+np.random.randint(0,5)]
self._cursor[b] = (self._cursor[b]+1)%self._prices_length
return batch_data,batch_labels
def unroll_batches(self):
unroll_data,unroll_labels = [],[]
init_data, init_label = None,None
for ui in range(self._num_unroll):
data, labels = self.next_batch()
unroll_data.append(data)
unroll_labels.append(labels)
return unroll_data, unroll_labels
def reset_indices(self):
for b in range(self._batch_size):
self._cursor[b] = np.random.randint(0,min((b+1)*self._segments,self._prices_length-1))
dg = DataGeneratorSeq(train_data,5,5)
u_data, u_labels = dg.unroll_batches()
for ui,(dat,lbl) in enumerate(zip(u_data,u_labels)):
print('\n\nUnrolled index %d'%ui)
dat_ind = dat
lbl_ind = lbl
print('\tInputs: ',dat )
print('\n\tOutput:',lbl)
Unrolled index 0
Inputs: [0.03143791 0.6904868 0.82829314 0.32585657 0.11600105]
Output: [0.08698314 0.68685144 0.8329321 0.33355275 0.11785509]
Unrolled index 1
Inputs: [0.06067836 0.6890754 0.8325337 0.32857886 0.11785509]
Output: [0.15261841 0.68685144 0.8325337 0.33421066 0.12106793]
Unrolled index 2
Inputs: [0.08698314 0.68685144 0.8329321 0.33078218 0.11946969]
Output: [0.11098009 0.6848606 0.83387965 0.33421066 0.12106793]
Unrolled index 3
Inputs: [0.11098009 0.6858036 0.83294916 0.33219692 0.12106793]
Output: [0.132895 0.6836884 0.83294916 0.33219692 0.12288672]
Unrolled index 4
Inputs: [0.132895 0.6848606 0.833369 0.33355275 0.12158521]
Output: [0.15261841 0.6836884 0.83383167 0.33355275 0.12230608]
Definición de hiperparámetros
En esta sección, definirá varios hiperparámetros. D es la dimensionalidad de la entrada. Es sencillo, ya que se toma el precio anterior de la acción como entrada y se predice el siguiente, que debería ser 1.
Luego tienes num_unrollings, este es un hiperparámetro relacionado con la retropropagación a través del tiempo (BPTT) que se utiliza para optimizar el modelo LSTM. Denota cuántos pasos de tiempo continuo se consideran para un único paso de optimización. En lugar de optimizar el modelo considerando un único paso temporal, se optimiza la red considerando num_unrollings pasos temporales. Cuanto más grande, mejor.
Luego tienes la batch_size. El tamaño del lote es el número de muestras de datos que se consideran en un único paso temporal.
A continuación se define num_nodes que representa el número de neuronas ocultas en cada celda. Puedes ver que hay tres capas de LSTMs en este ejemplo.
D = 1 # Dimensionality of the data. Since your data is 1-D this would be 1
num_unrollings = 50 # Number of time steps you look into the future.
batch_size = 500 # Number of samples in a batch
num_nodes = [200,200,150] # Number of hidden nodes in each layer of the deep LSTM stack we're using
n_layers = len(num_nodes) # number of layers
dropout = 0.2 # dropout amount
tf.reset_default_graph() # This is important in case you run this multiple times
Definición de entradas y salidas
A continuación se definen los marcadores de posición para las entradas y etiquetas de entrenamiento. Esto es muy sencillo, ya que tiene una lista de marcadores de posición de entrada, donde cada marcador de posición contiene un único lote de datos. Y la lista tiene num_unrollings marcadores de posición, que se utilizarán a la vez para un solo paso de optimización.
# Input data.
train_inputs, train_outputs = [],[]
# You unroll the input over time defining placeholders for each time step
for ui in range(num_unrollings):
train_inputs.append(tf.placeholder(tf.float32, shape=[batch_size,D],name='train_inputs_%d'%ui))
train_outputs.append(tf.placeholder(tf.float32, shape=[batch_size,1], name = 'train_outputs_%d'%ui))
Definición de los parámetros de las capas LSTM y de regresión
Tendrá tres capas de LSTMs y una capa de regresión lineal, denotadas por w y b, que toma la salida de la última celda de Memoria a Largo Corto Plazo y emite la predicción para el siguiente paso de tiempo. Puede utilizar MultiRNNCell en TensorFlow para encapsular los tres objetos LSTMCell que ha creado. Además, puede tener el abandono implementado células LSTM, ya que mejoran el rendimiento y reducir el sobreajuste.
lstm_cells = [
tf.contrib.rnn.LSTMCell(num_units=num_nodes[li],
state_is_tuple=True,
initializer= tf.contrib.layers.xavier_initializer()
)
for li in range(n_layers)]
drop_lstm_cells = [tf.contrib.rnn.DropoutWrapper(
lstm, input_keep_prob=1.0,output_keep_prob=1.0-dropout, state_keep_prob=1.0-dropout
) for lstm in lstm_cells]
drop_multi_cell = tf.contrib.rnn.MultiRNNCell(drop_lstm_cells)
multi_cell = tf.contrib.rnn.MultiRNNCell(lstm_cells)
w = tf.get_variable('w',shape=[num_nodes[-1], 1], initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable('b',initializer=tf.random_uniform([1],-0.1,0.1))
Cálculo de la salida LSTM y alimentación a la capa de regresión para obtener la predicción final.
En esta sección, primero se crean las variables de TensorFlow (c y h) que contendrán el estado de la celda y el estado oculto de la celda de Memoria Larga a Corto Plazo. Luego se transforma la lista de train_inputs para que tenga la forma de [num_unrollings, batch_size, D], esto es necesario para calcular las salidas con la función tf.nn.dynamic_rnn. A continuación, se calculan las salidas LSTM con la función tf.nn.dynamic_rnn y se vuelve a dividir la salida en una lista de tensores num_unrolling. la pérdida entre las predicciones y los precios reales de las acciones.
# Create cell state and hidden state variables to maintain the state of the LSTM
c, h = [],[]
initial_state = []
for li in range(n_layers):
c.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
h.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
initial_state.append(tf.contrib.rnn.LSTMStateTuple(c[li], h[li]))
# Do several tensor transofmations, because the function dynamic_rnn requires the output to be of
# a specific format. Read more at: https://www.tensorflow.org/api_docs/python/tf/nn/dynamic_rnn
all_inputs = tf.concat([tf.expand_dims(t,0) for t in train_inputs],axis=0)
# all_outputs is [seq_length, batch_size, num_nodes]
all_lstm_outputs, state = tf.nn.dynamic_rnn(
drop_multi_cell, all_inputs, initial_state=tuple(initial_state),
time_major = True, dtype=tf.float32)
all_lstm_outputs = tf.reshape(all_lstm_outputs, [batch_size*num_unrollings,num_nodes[-1]])
all_outputs = tf.nn.xw_plus_b(all_lstm_outputs,w,b)
split_outputs = tf.split(all_outputs,num_unrollings,axis=0)
Cálculo de pérdidas y optimizador
Ahora, calcularás la pérdida. Sin embargo, debe tener en cuenta que existe una característica única a la hora de calcular la pérdida. Para cada lote de predicciones y salidas verdaderas, se calcula el Error Cuadrático Medio. Y se suman (no se promedian) todas estas pérdidas medias al cuadrado. Por último, define el optimizador que vas a utilizar para optimizar la red neuronal. En este caso, puede utilizar Adam, que es un optimizador muy reciente y de buen rendimiento.
# When calculating the loss you need to be careful about the exact form, because you calculate
# loss of all the unrolled steps at the same time
# Therefore, take the mean error or each batch and get the sum of that over all the unrolled steps
print('Defining training Loss')
loss = 0.0
with tf.control_dependencies([tf.assign(c[li], state[li][0]) for li in range(n_layers)]+
[tf.assign(h[li], state[li][1]) for li in range(n_layers)]):
for ui in range(num_unrollings):
loss += tf.reduce_mean(0.5*(split_outputs[ui]-train_outputs[ui])**2)
print('Learning rate decay operations')
global_step = tf.Variable(0, trainable=False)
inc_gstep = tf.assign(global_step,global_step + 1)
tf_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
tf_min_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
learning_rate = tf.maximum(
tf.train.exponential_decay(tf_learning_rate, global_step, decay_steps=1, decay_rate=0.5, staircase=True),
tf_min_learning_rate)
# Optimizer.
print('TF Optimization operations')
optimizer = tf.train.AdamOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 5.0)
optimizer = optimizer.apply_gradients(
zip(gradients, v))
print('\tAll done')
Defining training Loss
Learning rate decay operations
TF Optimization operations
All done
Cálculos relacionados con la predicción
Aquí se definen las operaciones de TensorFlow relacionadas con la predicción. En primer lugar, defina un marcador de posición para alimentar la entrada (sample_inputs), después, de forma similar a la etapa de entrenamiento, defina las variables de estado para la predicción (sample_c y sample_h). Finalmente se calcula la predicción con la función tf.nn.dynamic_rnn y luego se envía la salida a través de la capa de regresión (w y b). También debe definir la operación reset_sample_state, que restablece el estado de la celda y el estado oculto. Debe ejecutar esta operación al principio, cada vez que realice una secuencia de predicciones.
print('Defining prediction related TF functions')
sample_inputs = tf.placeholder(tf.float32, shape=[1,D])
# Maintaining LSTM state for prediction stage
sample_c, sample_h, initial_sample_state = [],[],[]
for li in range(n_layers):
sample_c.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
sample_h.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
initial_sample_state.append(tf.contrib.rnn.LSTMStateTuple(sample_c[li],sample_h[li]))
reset_sample_states = tf.group(*[tf.assign(sample_c[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)],
*[tf.assign(sample_h[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)])
sample_outputs, sample_state = tf.nn.dynamic_rnn(multi_cell, tf.expand_dims(sample_inputs,0),
initial_state=tuple(initial_sample_state),
time_major = True,
dtype=tf.float32)
with tf.control_dependencies([tf.assign(sample_c[li],sample_state[li][0]) for li in range(n_layers)]+
[tf.assign(sample_h[li],sample_state[li][1]) for li in range(n_layers)]):
sample_prediction = tf.nn.xw_plus_b(tf.reshape(sample_outputs,[1,-1]), w, b)
print('\tAll done')
Defining prediction related TF functions
All done
Ejecución del LSTM
Aquí entrenará y predecirá los movimientos del precio de las acciones durante varias épocas y verá si las predicciones mejoran o empeoran con el tiempo. Sigue el siguiente procedimiento.
- Definir un conjunto de puntos de partida (
test_points_seq) en la serie temporal para evaluar el modelo. - Para cada época
- Para la longitud de secuencia completa de los datos de entrenamiento
- Desenrolle un conjunto de lotes
num_unrollings - Entrenar la red neuronal con los lotes desenrollados
- Desenrolle un conjunto de lotes
- Calcular la pérdida media de formación
- Para cada punto de partida del conjunto de pruebas
- Actualizar el estado LSTM iterando a través de los puntos de datos anteriores
num_unrollingsencontrados antes del punto de prueba. - Hacer predicciones para
n_predict_oncepasos continuamente, utilizando la predicción anterior como la entrada actual - Calcule la pérdida de MSE entre los puntos
n_predict_oncepredichos y los precios reales de las acciones en esos momentos.
- Actualizar el estado LSTM iterando a través de los puntos de datos anteriores
- Para la longitud de secuencia completa de los datos de entrenamiento
epochs = 30
valid_summary = 1 # Interval you make test predictions
n_predict_once = 50 # Number of steps you continously predict for
train_seq_length = train_data.size # Full length of the training data
train_mse_ot = [] # Accumulate Train losses
test_mse_ot = [] # Accumulate Test loss
predictions_over_time = [] # Accumulate predictions
session = tf.InteractiveSession()
tf.global_variables_initializer().run()
# Used for decaying learning rate
loss_nondecrease_count = 0
loss_nondecrease_threshold = 2 # If the test error hasn't increased in this many steps, decrease learning rate
print('Initialized')
average_loss = 0
# Define data generator
data_gen = DataGeneratorSeq(train_data,batch_size,num_unrollings)
x_axis_seq = []
# Points you start your test predictions from
test_points_seq = np.arange(11000,12000,50).tolist()
for ep in range(epochs):
# ========================= Training =====================================
for step in range(train_seq_length//batch_size):
u_data, u_labels = data_gen.unroll_batches()
feed_dict = {}
for ui,(dat,lbl) in enumerate(zip(u_data,u_labels)):
feed_dict[train_inputs[ui]] = dat.reshape(-1,1)
feed_dict[train_outputs[ui]] = lbl.reshape(-1,1)
feed_dict.update({tf_learning_rate: 0.0001, tf_min_learning_rate:0.000001})
_, l = session.run([optimizer, loss], feed_dict=feed_dict)
average_loss += l
# ============================ Validation ==============================
if (ep+1) % valid_summary == 0:
average_loss = average_loss/(valid_summary*(train_seq_length//batch_size))
# The average loss
if (ep+1)%valid_summary==0:
print('Average loss at step %d: %f' % (ep+1, average_loss))
train_mse_ot.append(average_loss)
average_loss = 0 # reset loss
predictions_seq = []
mse_test_loss_seq = []
# ===================== Updating State and Making Predicitons ========================
for w_i in test_points_seq:
mse_test_loss = 0.0
our_predictions = []
if (ep+1)-valid_summary==0:
# Only calculate x_axis values in the first validation epoch
x_axis=[]
# Feed in the recent past behavior of stock prices
# to make predictions from that point onwards
for tr_i in range(w_i-num_unrollings+1,w_i-1):
current_price = all_mid_data[tr_i]
feed_dict[sample_inputs] = np.array(current_price).reshape(1,1)
_ = session.run(sample_prediction,feed_dict=feed_dict)
feed_dict = {}
current_price = all_mid_data[w_i-1]
feed_dict[sample_inputs] = np.array(current_price).reshape(1,1)
# Make predictions for this many steps
# Each prediction uses previous prediciton as it's current input
for pred_i in range(n_predict_once):
pred = session.run(sample_prediction,feed_dict=feed_dict)
our_predictions.append(np.asscalar(pred))
feed_dict[sample_inputs] = np.asarray(pred).reshape(-1,1)
if (ep+1)-valid_summary==0:
# Only calculate x_axis values in the first validation epoch
x_axis.append(w_i+pred_i)
mse_test_loss += 0.5*(pred-all_mid_data[w_i+pred_i])**2
session.run(reset_sample_states)
predictions_seq.append(np.array(our_predictions))
mse_test_loss /= n_predict_once
mse_test_loss_seq.append(mse_test_loss)
if (ep+1)-valid_summary==0:
x_axis_seq.append(x_axis)
current_test_mse = np.mean(mse_test_loss_seq)
# Learning rate decay logic
if len(test_mse_ot)>0 and current_test_mse > min(test_mse_ot):
loss_nondecrease_count += 1
else:
loss_nondecrease_count = 0
if loss_nondecrease_count > loss_nondecrease_threshold :
session.run(inc_gstep)
loss_nondecrease_count = 0
print('\tDecreasing learning rate by 0.5')
test_mse_ot.append(current_test_mse)
print('\tTest MSE: %.5f'%np.mean(mse_test_loss_seq))
predictions_over_time.append(predictions_seq)
print('\tFinished Predictions')
Initialized
Average loss at step 1: 1.703350
Test MSE: 0.00318
Finished Predictions
...
...
...
Average loss at step 30: 0.033753
Test MSE: 0.00243
Finished Predictions
Visualización de las predicciones
Puedes ver cómo la pérdida de MSE disminuye con la cantidad de entrenamiento. Es una buena señal de que el modelo está aprendiendo algo útil. Para cuantificar sus resultados, puede comparar la pérdida de MSE de la red con la pérdida de MSE que obtuvo al hacer la media estándar (0,004). Puedes ver que el LSTM lo hace mejor que el promedio estándar. Y usted sabe que el promedio estándar (aunque no es perfecto) siguió razonablemente los verdaderos movimientos de los precios de las acciones.
best_prediction_epoch = 28 # replace this with the epoch that you got the best results when running the plotting code
plt.figure(figsize = (18,18))
plt.subplot(2,1,1)
plt.plot(range(df.shape[0]),all_mid_data,color='b')
# Plotting how the predictions change over time
# Plot older predictions with low alpha and newer predictions with high alpha
start_alpha = 0.25
alpha = np.arange(start_alpha,1.1,(1.0-start_alpha)/len(predictions_over_time[::3]))
for p_i,p in enumerate(predictions_over_time[::3]):
for xval,yval in zip(x_axis_seq,p):
plt.plot(xval,yval,color='r',alpha=alpha[p_i])
plt.title('Evolution of Test Predictions Over Time',fontsize=18)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.xlim(11000,12500)
plt.subplot(2,1,2)
# Predicting the best test prediction you got
plt.plot(range(df.shape[0]),all_mid_data,color='b')
for xval,yval in zip(x_axis_seq,predictions_over_time[best_prediction_epoch]):
plt.plot(xval,yval,color='r')
plt.title('Best Test Predictions Over Time',fontsize=18)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.xlim(11000,12500)
plt.show()
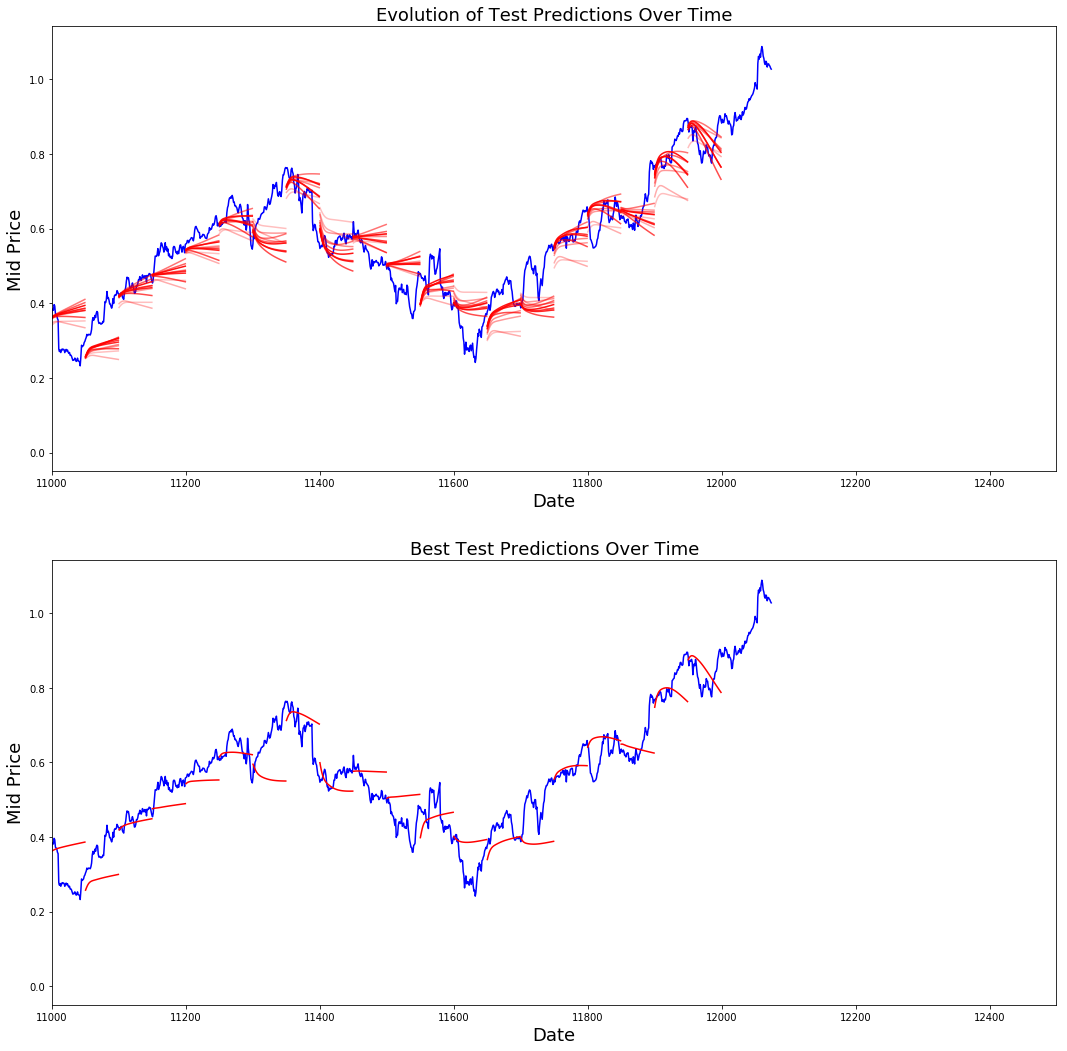
Aunque no son perfectas, las LSTM parecen capaces de predecir correctamente el comportamiento del precio de las acciones la mayor parte del tiempo. Tenga en cuenta que está haciendo predicciones aproximadamente en el rango de 0 y 1,0 (es decir, no los precios reales de las acciones). Esto está bien, porque estás prediciendo el movimiento del precio de las acciones, no los precios en sí.
Observaciones finales
Espero que este tutorial te haya resultado útil. Debo mencionar que fue una experiencia gratificante para mí. En este tutorial, aprendí lo difícil que puede ser crear un modelo capaz de predecir correctamente los movimientos de los precios de las acciones. Empezaste con una motivación de por qué necesitas modelar los precios de las acciones. A continuación, se ofrece una explicación y un código para descargar los datos. A continuación, has estudiado dos técnicas de promediación que permiten hacer predicciones un paso en el futuro. A continuación has visto que estos métodos son inútiles cuando necesitas predecir más de un paso en el futuro. A continuación, se discutió cómo se pueden utilizar los LSTM para hacer predicciones a muchos pasos en el futuro. Por último, ha visualizado los resultados y ha visto que su modelo (aunque no es perfecto) es bastante bueno a la hora de predecir correctamente los movimientos del precio de las acciones.
Si desea obtener más información sobre el aprendizaje profundo, asegúrese de echar un vistazo a nuestro curso Aprendizaje profundo en Python. Cubre los conceptos básicos, así como la forma de construir una red neuronal por su cuenta en Keras. Se trata de un paquete diferente a TensorFlow, que se utilizará en este tutorial, pero la idea es la misma.
A continuación, expongo varias conclusiones de este tutorial.
-
Predecir el precio y el movimiento de las acciones es una tarea extremadamente difícil. Personalmente, no creo que haya que dar por sentado ninguno de los modelos de predicción bursátil que existen y confiar ciegamente en ellos. Sin embargo, los modelos pueden predecir correctamente el movimiento del precio de las acciones la mayoría de las veces, pero no siempre.
-
No se deje engañar por los artículos por ahí que muestra las curvas de predicción que se superpone perfectamente los precios de las acciones reales. Esto se puede reproducir con una simple técnica de promediado y en la práctica es inútil. Lo más sensato es predecir los movimientos del precio de las acciones.
-
Los hiperparámetros del modelo son extremadamente sensibles a los resultados que se obtienen. Por lo tanto, una muy buena cosa a hacer sería ejecutar alguna técnica de optimización de hiperparámetros (por ejemplo, búsqueda de cuadrícula / búsqueda aleatoria) en los hiperparámetros. A continuación enumero algunos de los hiperparámetros más críticos
- El ritmo de aprendizaje del optimizador
- Número de capas y número de unidades ocultas en cada capa
- El optimizador. Encontré a Adam para llevar a cabo la mejor
- Tipo de modelo. Puede probar GRU/ LSTM estándar/ LSTM con Peepholes y evaluar la diferencia de rendimiento.
-
¡En este tutorial has hecho algo defectuoso (debido al pequeño tamaño de los datos)! Es decir, has utilizado la pérdida de la prueba para decaer la tasa de aprendizaje. De este modo, se filtra indirectamente información sobre el conjunto de pruebas en el procedimiento de formación. Una forma mejor de manejar esto es tener un conjunto de validación separado (aparte del conjunto de prueba) y decaer la tasa de aprendizaje con respecto al rendimiento del conjunto de validación.
Si quieres ponerte en contacto conmigo, envíame un correo electrónico a thushv@gmail.com o conéctate conmigo en LinkedIn.
Referencias
He consultado este repositorio para entender cómo utilizar los LSTM para predecir acciones. Pero los detalles pueden ser muy diferentes de la implementación que se encuentra en la referencia.


