Tutorial de PyTorch: Construir una red neuronal sencilla desde cero

En este tutorial de PyTorch, cubriremos las funciones básicas de las redes neuronales y construiremos las nuestras desde cero. El objetivo principal de este artículo es demostrar los fundamentos de PyTorch, una biblioteca de tensores de aprendizaje profundo optimizada, y proporcionarte información detallada sobre el funcionamiento de las redes neuronales. 

Nota: Consulta este DataCamp Workspace para seguir el código escrito en este artículo.

¿Qué son las redes neuronales? 

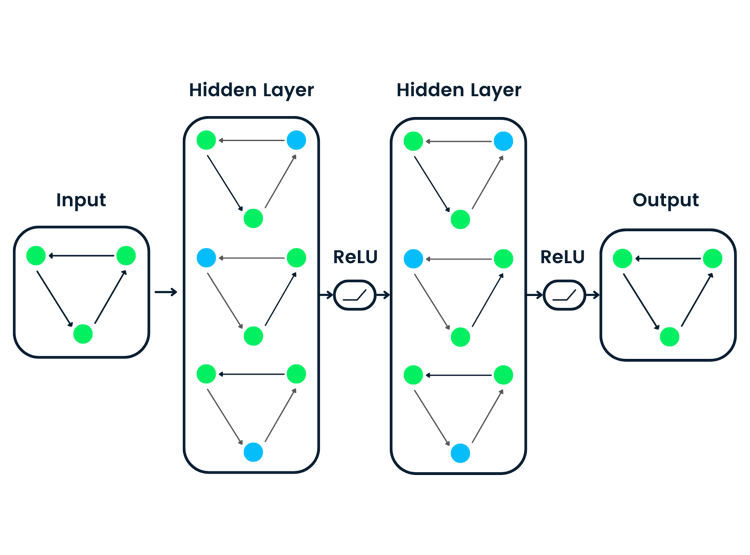
Las redes neuronales también se denominan redes neuronales artificiales (ANN). La arquitectura constituye la base del aprendizaje profundo, que no es más que un subconjunto del machine learning que se ocupa de algoritmos que se inspiran en la estructura y la función del cerebro humano.  En pocas palabras, las redes neuronales constituyen la base de arquitecturas que imitan la forma en que las neuronas biológicas se señalan. 

En consecuencia, a menudo encontrarás recursos que dedican los primeros cinco minutos a trazar la estructura neuronal del cerebro humano para ayudarte a conceptualizar visualmente cómo funciona una red neuronal. Sin embargo, cuando no dispones de cinco minutos extra, es más fácil definir una red neuronal como una función que asigna entradas a salidas deseadas. 

La arquitectura genérica de la red neuronal consiste en lo siguiente

• Capa de entrada: Los datos se introducen en la red mediante la capa de entrada. El número de neuronas de la capa de entrada es equivalente al número de características de los datos. Técnicamente, la capa de entrada no se considera una de las capas de la red, porque en este punto no se produce computación. 
• Capa oculta: Las capas situadas entre las capas de entrada y salida se denominan capas ocultas. Una red puede tener un número arbitrario de capas ocultas: cuantas más capas ocultas haya, más compleja será la red. 
• Capa de salida: La capa de salida se utiliza para hacer una predicción. 
• Neuronas: Cada capa tiene un conjunto de neuronas que interactúan con neuronas de otras capas. 
• Función de activación: Realiza transformaciones no lineales para ayudar al modelo a aprender patrones complejos a partir de los datos. 

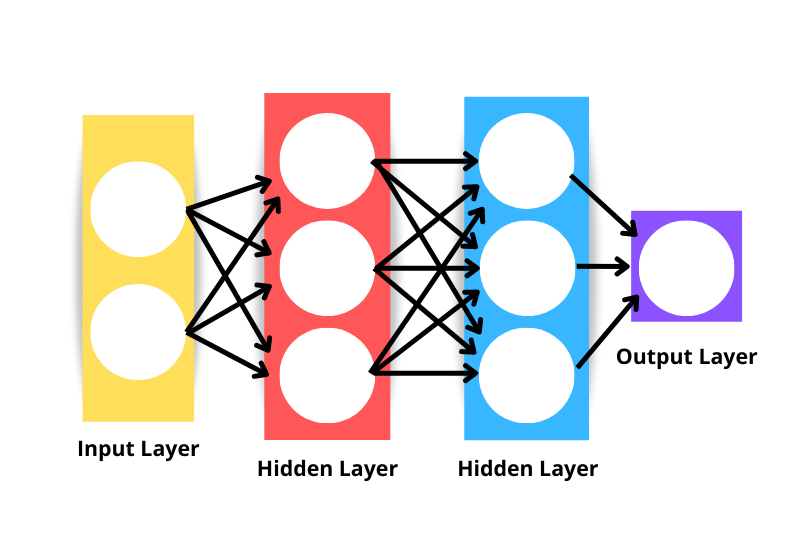
Observa que la red neuronal mostrada en la imagen anterior se consideraría una red neuronal de tres capas y no de cuatro, porque no incluimos la capa de entrada como capa. Por tanto, el número de capas de una red es el número de capas ocultas más la capa de salida.

¿Cómo funcionan las redes neuronales? 

Vamos a descomponer el algoritmo en componentes menores para comprender mejor cómo funcionan las redes neuronales.

Inicialización del peso

La inicialización del peso es el primer componente de la arquitectura de la red neuronal. Los pesos iniciales los fijamos para definir el punto de partida del proceso de optimización del modelo de red neuronal. 

La forma en que fijamos nuestros pesos es importante, sobre todo cuando construimos redes profundas. Esto se debe a que las redes profundas son más propensas a sufrir el problema de explosión o desvanecimiento de gradiente. Los problemas de desvanecimiento o explosión de gradiente son dos conceptos que quedan fuera del alcance de este artículo, pero ambos describen una situación en la que el algoritmo no consigue aprender. 

Aunque la inicialización del peso no resuelve completamente el problema de desvanecimiento o explosión de gradiente, sin duda contribuye a prevenirlo. 

He aquí algunos enfoques comunes de inicialización del peso: 

Inicialización cero

Inicialización cero significa que los pesos se inicializan como cero. No es una buena solución, ya que nuestra red neuronal no rompería la simetría: no aprendería. 

Siempre que se utilice un valor constante para inicializar los pesos de una red neuronal, podemos esperar que su rendimiento sea deficiente, ya que todas las capas aprenderán lo mismo. Si todas las salidas de las unidades ocultas tienen la misma influencia en el coste, los gradientes serán idénticos. 

Inicialización aleatoria

La inicialización aleatoria rompe la simetría, lo que significa que es mejor que la inicialización cero, pero algunos factores pueden determinar la calidad general del modelo. 

Por ejemplo, si los pesos se inicializan aleatoriamente con valores grandes, podemos esperar que cada multiplicación de matrices dé como resultado un valor mucho mayor. Cuando se aplica una función de activación sigmoide en estas situaciones, el resultado es un valor próximo a uno, lo que ralentiza el aprendizaje.

Otra situación en la que la inicialización aleatoria puede causar problemas es si los pesos se inicializan aleatoriamente con valores pequeños. En este caso, cada multiplicación de matrices producirá valores significativamente menores, y aplicando una función sigmoide se obtendrá un valor más próximo a cero, lo que también ralentiza el aprendizaje. 

Inicialización de Xavier/Glorot 

Una inicialización de Xavier o Glorot (se le da cualquiera de los dos nombres) es un enfoque heurístico utilizado para inicializar los pesos. Es habitual ver este enfoque de inicialización siempre que se aplica una función de activación tanh o sigmoide a la media ponderada. El enfoque se propuso por primera vez en 2010 en un trabajo de investigación titulado Understanding the difficulty of training deep feedforward neural networks, de Xavier Glorot y Yoshua Bengio. El objetivo de esta técnica de inicialización es mantener igual la varianza en toda la red para evitar el problema de explosión o desvanecimiento de gradiente. 

Inicialización de He/Kaiming 

La inicialización de He o Kaiming es otro enfoque heurístico. La diferencia de las heurísticas de He y Xavier es que la inicialización de He utiliza un factor de escala diferente para los pesos que tiene en cuenta la no linealidad de las funciones de activación. 

Por tanto, cuando se utiliza la función de activación ReLU en las capas, la inicialización de He es el enfoque recomendado. Puedes obtener más información sobre este enfoque en Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, de He et al.

Propagación hacia delante

Las redes neuronales funcionan tomando una media ponderada más un término de sesgo y aplicando una función de activación para añadir una transformación no lineal. En la formulación de la media ponderada, cada peso determina la importancia de cada característica (es decir, cuánto contribuye a predecir la salida).

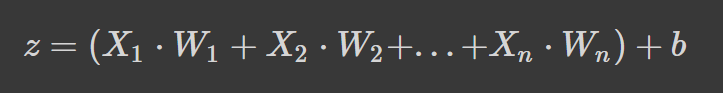
La fórmula anterior es la media ponderada más un término de sesgo donde 

• z es la suma ponderada de la entrada de una neurona
• Wn indica los pesos
• Xn indica las variables independientes, y
• b es el término de sesgo.

Si la fórmula te resulta familiar, es porque se trata de una regresión lineal. Sin introducir la no linealidad en las neuronas, tendríamos la regresión lineal, que es un modelo sencillo. La transformación no lineal permite a nuestra red neuronal aprender patrones complejos. 

Funciones de activación

Ya hemos aludido a algunas funciones de activación en la sección de inicialización del peso, pero ahora ya conoces su importancia en la arquitectura de una red neuronal.

Profundicemos en algunas funciones de activación habituales que es probable que veas cuando leas artículos de investigación y el código de otras personas.  

Sigmoide

La función sigmoide se caracteriza por una curva en forma de S delimitada entre los valores cero y uno. Es una función diferenciable, lo que significa que la pendiente de la curva puede encontrarse en dos puntos cualesquiera, y monótona, lo que significa que no es totalmente creciente ni decreciente. Normalmente utilizarás la función de activación sigmoide para los problemas de clasificación binaria.

He aquí cómo puedes visualizar tu propia función sigmoide utilizando Python: 

# Sigmoid function in Python
import matplotlib.pyplot as plt
import numpy as np




x = np.linspace(-5, 5, 50)
z = 1/(1 + np.exp(-x))




plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()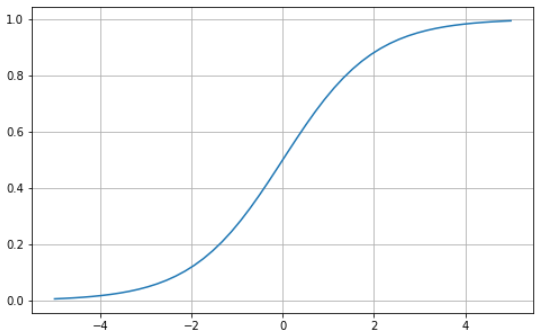

Tanh

La tangente hiperbólica (tanh) tiene la misma curva en forma de S que la función sigmoide, pero los valores están acotados entre -1 y 1. Así, las entradas pequeñas se asignan más cerca de -1, y las entradas mayores se asignan más cerca de 1.

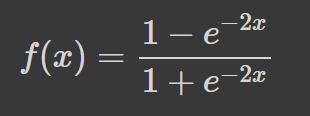
Aquí tienes un ejemplo de función tanh visualizada con Python: 

# tanh function in Python
import matplotlib.pyplot as plt
import numpy as np




x = np.linspace(-5, 5, 50)
z = np.tanh(x)


plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()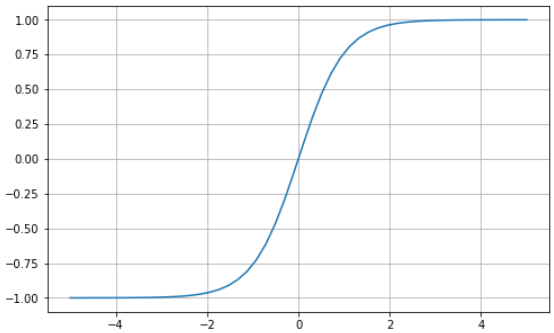

SoftMax

La función SoftMax se utiliza generalmente como función de activación en la capa de salida. Es una generalización de la función sigmoide a varias dimensiones. Por tanto, se utiliza en redes neuronales para predecir la pertenencia a clases con más de dos etiquetas. 

Unidad lineal rectificada (ReLU)

Utilizar la función sigmoide o tanh para construir redes neuronales profundas es arriesgado, ya que es más probable que sufran el problema de desvanecimiento de gradiente. La función de activación de unidad lineal rectificada (ReLU) surgió como solución a este problema y suele ser la función de activación predeterminada de varias redes neuronales. 

Aquí tienes un ejemplo visual de la función ReLU utilizando Python: 

# ReLU in Python
import matplotlib.pyplot as plt
import numpy as np


x = np.linspace(-5, 5, 50)
z = [max(0, i) for i in x]


plt.subplots(figsize=(8, 5))
plt.plot(x, z)
plt.grid()
plt.show()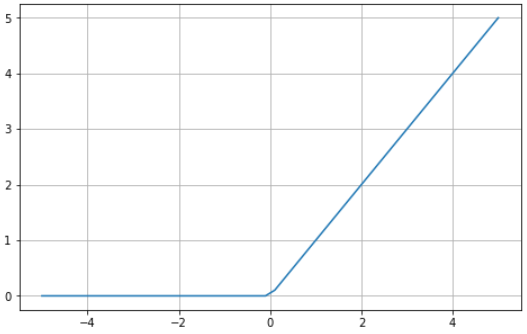

ReLU está acotada entre cero e infinito: observa que, para valores de entrada menores o iguales que cero, la función devuelve cero y, para valores superiores a cero, la función devuelve el valor de entrada proporcionado (es decir, si introduces dos, se devolverá dos). En definitiva, la función ReLU se comporta de forma muy similar a una función lineal, por lo que es mucho más fácil de optimizar e implementar. 

El proceso que va de la capa de entrada a la de salida se conoce como paso hacia delante o propagación hacia delante. Durante esta fase, las salidas generadas por el modelo se utilizan para computar una función de coste que determine el rendimiento de la red neuronal después de cada iteración. A continuación, esta información se transmite de nuevo al modelo para corregir los pesos, de modo que el modelo pueda hacer mejores predicciones, en un proceso conocido como propagación hacia atrás de los errores. 

Propagación hacia atrás de los errores

Al final del primer paso hacia delante, la red hace predicciones utilizando los pesos inicializados, que no están ajustados. Por tanto, es muy probable que las predicciones que haga el modelo no sean exactas. Utilizando la pérdida calculada a partir de la propagación hacia delante, volvemos a pasar la información por la red para ajustar los pesos en un proceso conocido como propagación hacia atrás de los errores. 

En definitiva, utilizamos la función de optimización para identificar los pesos que pueden reducir la tasa de error, haciendo que el modelo sea más fiable y aumentando su capacidad de generalización a nuevas instancias. Las matemáticas que explican cómo funciona esto están fuera del alcance de este artículo, pero, si te interesan, puedes aprender más sobre la propagación hacia atrás de los errores en nuestro curso Introducción al aprendizaje profundo en Python.

Tutorial de PyTorch: Un recorrido paso a paso para construir una red neuronal desde cero

En esta sección del artículo, construiremos un modelo sencillo de red neuronal artificial utilizando la biblioteca PyTorch. Consulta este DataCamp Workspace para seguir el código

PyTorch es una de las bibliotecas más populares para el aprendizaje profundo. Proporciona una experiencia de depuración mucho más directa que TensorFlow. Tiene otras ventajas, como el entrenamiento distribuido, un ecosistema robusto, compatibilidad con la nube, escritura de código listo para producción, etc. Puedes aprender más sobre PyTorch en el programa Introducción al aprendizaje profundo con PyTorch. 

Entremos en el tutorial. 

Definición y preparación de datos 

El conjunto de datos que utilizaremos en nuestro tutorial es make_circles de scikit-learn: consulta la documentación. Es un conjunto de datos de juguetes que contiene un círculo grande con un círculo menor en un plano bidimensional y dos características. Para nuestra demostración, utilizamos 10 000 muestras y añadimos una desviación típica de 0,05 de ruido gaussiano a los datos. 

Antes de construir nuestra red neuronal, es una práctica recomendada dividir nuestros datos en conjuntos de entrenamiento y de prueba para poder evaluar el rendimiento del modelo en datos no vistos.

import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

# Create a dataset with 10,000 samples.
X, y = make_circles(n_samples = 10000,
                    noise= 0.05,
                    random_state=26)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.33, random_state=26)

# Visualize the data.
fig, (train_ax, test_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(10, 5))
train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Spectral)
train_ax.set_title("Training Data")
train_ax.set_xlabel("Feature #0")
train_ax.set_ylabel("Feature #1")

test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
test_ax.set_xlabel("Feature #0")
test_ax.set_title("Testing data")
plt.show()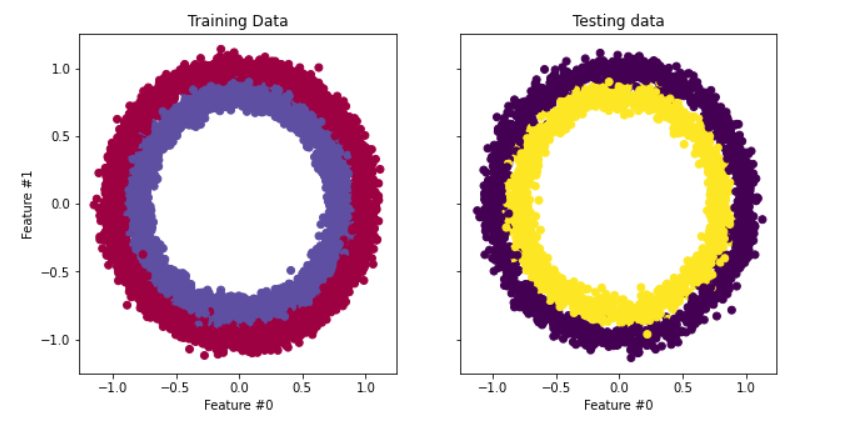

El siguiente paso es convertir los datos de entrenamiento y prueba de matrices NumPy a tensores PyTorch. Para ello, vamos a crear un conjunto de datos personalizado para nuestros archivos de entrenamiento y de prueba. También vamos a aprovechar el módulo Dataloader de PyTorch para poder entrenar nuestros datos por lotes. Aquí tienes el código: 

import warnings
warnings.filterwarnings("ignore")

!pip install torch -q

import torch
import numpy as np
from torch.utils.data import Dataset, DataLoader

# Convert data to torch tensors
class Data(Dataset):
    def __init__(self, X, y):
        self.X = torch.from_numpy(X.astype(np.float32))
        self.y = torch.from_numpy(y.astype(np.float32))
        self.len = self.X.shape[0]
       
    def __getitem__(self, index):
        return self.X[index], self.y[index]
   
    def __len__(self):
        return self.len
   
batch_size = 64

# Instantiate training and test data
train_data = Data(X_train, y_train)
train_dataloader = DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)

test_data = Data(X_test, y_test)
test_dataloader = DataLoader(dataset=test_data, batch_size=batch_size, shuffle=True)

# Check it's working
for batch, (X, y) in enumerate(train_dataloader):
    print(f"Batch: {batch+1}")
    print(f"X shape: {X.shape}")
    print(f"y shape: {y.shape}")
    break


"""
Batch: 1
X shape: torch.Size([64, 2])
y shape: torch.Size([64])
"""

Ahora pasemos a implementar y entrenar nuestra red neuronal. 

Implementación de redes neuronales y entrenamiento de modelos

Vamos a implementar una red neuronal sencilla de dos capas que utiliza la función de activación ReLU (torch.nn.functional.relu). Para ello, vamos a crear una clase llamada NeuralNetwork que hereda de nn.Module, que es la clase básica para todos los módulos de redes neuronales construidos en PyTorch. 

Aquí tienes el código: 

import torch
from torch import nn
from torch import optim

input_dim = 2
hidden_dim = 10
output_dim = 1

class NeuralNetwork(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(NeuralNetwork, self).__init__()
        self.layer_1 = nn.Linear(input_dim, hidden_dim)
        nn.init.kaiming_uniform_(self.layer_1.weight, nonlinearity="relu")
        self.layer_2 = nn.Linear(hidden_dim, output_dim)
       
    def forward(self, x):
        x = torch.nn.functional.relu(self.layer_1(x))
        x = torch.nn.functional.sigmoid(self.layer_2(x))

        return x
       
model = NeuralNetwork(input_dim, hidden_dim, output_dim)
print(model)


"""
NeuralNetwork(
  (layer_1): Linear(in_features=2, out_features=10, bias=True)
  (layer_2): Linear(in_features=10, out_features=1, bias=True)
)
"""

Y eso es todo. 

Para entrenar el modelo, debemos definir una función de pérdida para calcular los gradientes y un optimizador para actualizar los parámetros. Para nuestra demostración, vamos a utilizar entropía cruzada binaria y descenso de gradiente estocástico con una tasa de aprendizaje de 0,1. 

learning_rate = 0.1

loss_fn = nn.BCELoss()

optimizer = torch.optim.SGD(model.parameters(), lr=lea

Entrenemos nuestro modelo

num_epochs = 100
loss_values = []


for epoch in range(num_epochs):
    for X, y in train_dataloader:
        # zero the parameter gradients
        optimizer.zero_grad()
       
        # forward + backward + optimize
        pred = model(X)
        loss = loss_fn(pred, y.unsqueeze(-1))
        loss_values.append(loss.item())
        loss.backward()
        optimizer.step()

print("Training Complete")

"""
Training Complete
"""

Como hemos seguido los valores de pérdida, podemos visualizar la pérdida del modelo a lo largo del tiempo. 

step = np.linspace(0, 100, 10500)

fig, ax = plt.subplots(figsize=(8,5))
plt.plot(step, np.array(loss_values))
plt.title("Step-wise Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.show()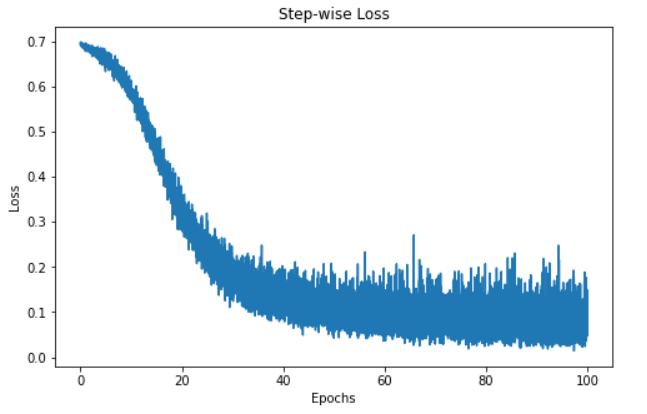

La visualización anterior muestra la pérdida de nuestro modelo a lo largo de 100 epochs. La pérdida empieza en 0,7 y disminuye de forma gradual, lo que nos informa de que nuestro modelo ha ido mejorando sus predicciones con el tiempo. Sin embargo, el modelo parece estancarse en torno a la marca de 60 epochs, lo que puede deberse a diferentes razones, como que el modelo se encuentre en la región de un mínimo local o global de la función de pérdida. 

Sin embargo, el modelo se ha entrenado y está listo para hacer predicciones sobre nuevas instancias; veamos cómo hacerlo en la siguiente sección.

Predicciones y evaluación de modelos

Hacer predicciones con nuestra red neuronal PyTorch es bastante sencillo. 

"""
We're not training so we don't need to calculate the gradients for our outputs
"""
with torch.no_grad():
    for X, y in test_dataloader:
        outputs = model(X)
        predicted = np.where(outputs < 0.5, 0, 1)
        predicted = list(itertools.chain(*predicted))
        y_pred.append(predicted)
        y_test.append(y)
        total += y.size(0)
        correct += (predicted == y.numpy()).sum().item()

print(f'Accuracy of the network on the 3300 test instances: {100 * correct // total}%')

"""
Accuracy of the network on the 3300 test instances: 97%
"""

Nota: Cada ejecución del código produciría una salida diferente, por lo que es posible que no obtengas los mismos resultados. 

El código anterior recorre en bucle los lotes de prueba, que se almacenan en la variable test_dataloader, sin calcular los gradientes. A continuación, predecimos las instancias del lote y almacenamos los resultados en una variable llamada Outputs. A continuación, determinamos establecer todos los valores menores que 0,5 en 0 y los iguales o mayores que 0,5 en 1. A continuación, estos valores se añaden a una lista para nuestras predicciones.

Después, añadimos las predicciones reales de las instancias del lote a una variable llamada Total. A continuación, calculamos el número de predicciones correctas identificando el número de predicciones iguales a las clases reales y sumándolas. El número total de predicciones correctas de cada lote se incrementa y se almacena en nuestra variable correcta.

Para calcular la exactitud del modelo global, multiplicamos el número de predicciones correctas por 100 (para obtener un porcentaje) y, a continuación, lo dividimos entre el número de instancias de nuestro conjunto de prueba. Nuestro modelo tuvo una exactitud del 97 %. Profundizamos más utilizando la matriz de confusión y classification_report de scikit-learn para comprender mejor el rendimiento de nuestro modelo.

from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix

import seaborn as sns


y_pred = list(itertools.chain(*y_pred))
y_test = list(itertools.chain(*y_test))


print(classification_report(y_test, y_pred))

"""
              precision    recall  f1-score   support

        0.0       0.98      0.97      0.98      1635
        1.0       0.98      0.98      0.98      1665

    accuracy                           0.98      3300
  macro avg       0.98      0.98      0.98      3300
weighted avg       0.98      0.98      0.98      3300

"""




cf_matrix = confusion_matrix(y_test, y_pred)

plt.subplots(figsize=(8, 5))

sns.heatmap(cf_matrix, annot=True, cbar=False, fmt="g")

plt.show()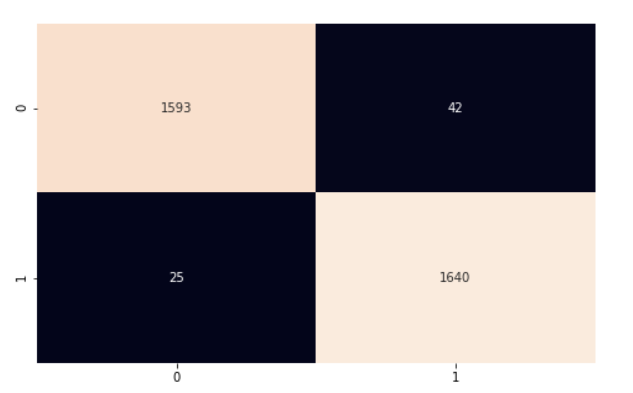

Nuestro modelo funciona bastante bien. Te animo a que explores el código y realices algunos cambios para recordar lo que hemos tratado en este artículo.  

En este tutorial de PyTorch, tratamos los fundamentos de las redes neuronales y utilizamos PyTorch, una biblioteca de Python para el aprendizaje profundo, para implementar nuestra red. Utilizamos el conjunto de datos del círculo de scikit-learn para entrenar una red neuronal de dos capas para la clasificación. A continuación, hicimos predicciones sobre los datos y evaluamos nuestros resultados utilizando el parámetro de exactitud.