Regresión lineal múltiple en R: tutorial con ejemplos

Los métodos de regresión se utilizan en distintos sectores para comprender qué variables influyen en un determinado tema de interés. 

Por ejemplo, los economistas pueden utilizarlos para analizar la relación entre el gasto de los consumidores y el crecimiento del producto interior bruto (PIB). Los funcionarios de la sanidad pública podrían querer comprender los costes de los individuos en función de su información histórica. En ambos casos, la atención no se centra en predecir escenarios individuales, sino en obtener una visión general de la relación global.

En este artículo, empezaremos por proporcionar una comprensión general de las regresiones. A continuación, explicaremos en qué se diferencian las regresiones lineales simples y múltiples, antes de sumergirnos en las implementaciones técnicas y proporcionar herramientas que te ayuden a comprender e interpretar los resultados de la regresión.

¿Qué es la regresión lineal múltiple?

Entendamos primero qué es una regresión lineal simple antes de sumergirnos en la regresión lineal múltiple, que no es más que una extensión de la regresión lineal simple.

Regresión lineal simple

Una regresión lineal simple pretende modelizar la relación entre la magnitud de una única variable independiente X y una variable dependiente Y, e intenta estimar exactamente cuánto cambiará Y cuando X cambie en una cantidad determinada. 

• La variable independiente X, también llamada predictor, es la variable utilizada para hacer la predicción. 
• La variable dependiente Y, también llamada respuesta, es la que intentamos predecir.

El aspecto "lineal" de la regresión lineal es que estamos intentando predecir Y a partir de X mediante la siguiente ecuación "lineal". 

Y = b0 + b1X 

• b0 es el intercepto de la recta de regresión, que corresponde al valor predicho cuando X es nulo. 
• b1 es la pendiente de la recta de regresión.

Entonces, ¿qué pasa con la regresión lineal múltiple?

Se trata del uso de la regresión lineal con múltiples variables, y la ecuación es:

Y = b0 + b1X1 + b2X2 + b3X3 + … + bnXn + e

• Y y b0 son los mismos que en el modelo de regresión lineal simple. 
• b1X1 representa el coeficiente de regresión (b1) sobre la primera variable independiente (X1). El mismo análisis se aplica a todos los demás coeficientes y variables de regresión. 
• e es el error del modelo (residuos), que define cuánta variación se introduce en el modelo al estimar Y.

Puede que no siempre obtengamos una línea recta en un caso de regresión múltiple. Sin embargo, podemos controlar la forma de la línea ajustando un modelo más apropiado. 

Estos son algunos de los elementos clave computados por la regresión lineal múltiple para encontrar la línea de mejor ajuste para cada predictor.

• Los coeficientes estimados para cada predictor. 
• R cuadrado del modelo, que corresponde a la proporción de varianza explicada por el modelo, y mide la fuerza de la relación entre el modelo y la variable dependiente Y en una cómoda escala de 0 a 100 %. 
• El valor p y la estadística t de cada coeficiente de regresión del modelo. Estas dos métricas se consideran el espejo la una de la otra, y miden hasta qué punto un coeficiente dado es estadísticamente significativo. Cuanto mayor sea el estadístico t (que va con el valor p cercano a 0), más significativo es el predictor, lo que significa que ese predictor debe mantenerse en el modelo. Por otra parte, una estadística t muy baja (valor p más alto) significa que el predictor debe descartarse.

Los supuestos de la regresión lineal múltiple

Un aspecto importante a la hora de construir un modelo de regresión lineal múltiple es asegurarse de que se cumplen los siguientes supuestos clave.

• Los valores individuales se distribuyen normalmente. Esto puede comprobarse mediante un gráfico de probabilidad normal o un histograma.
• Debe existir una relación lineal entre las variables dependientes e independientes. Esto puede ilustrarse mediante gráficos de dispersión que muestren una relación lineal o curvilínea.
• La multicolinealidad es otro supuesto, que significa que las variables independientes no están muy correlacionadas entre sí. La multicolinealidad dificulta la identificación de las variables que explican mejor la variable dependiente. Este supuesto se verifica con una matriz de correlaciones bivariadas de Pearson entre todas las variables independientes. Si no hay colinealidad en los datos, todos los valores deben ser inferiores a 0,8. 
• La homocedasticidad supone que la varianza de los errores residuales es similar según el valor de cada variable independiente. Una forma de comprobarlo es mediante un gráfico de los valores predichos frente a los valores residuales estandarizados, para ver si los puntos se distribuyen por igual en todos los valores de las variables independientes.

En los próximos apartados, abordaremos algunos de estos supuestos.

Guía paso a paso de la regresión lineal múltiple en R

En esta sección, nos sumergiremos en la implementación técnica de un modelo de regresión lineal múltiple con el lenguaje de programación R. 

Utilizaremos el conjunto de datos de rotación de clientes del espacio de trabajo de DataCamp para estimar el valor del cliente.

¿Qué entendemos por valor para el cliente? Básicamente, determina el valor que tiene un producto o servicio para un cliente, y podemos calcularlo de la siguiente manera: 

Customer Value = Benefit — Cost. Donde Beneficio y Coste son, respectivamente, el beneficio y el coste de un producto o un servicio. 

Este valor es mayor si la empresa puede ofrecer a los consumidores mayores beneficios y menores costes o, idealmente, una combinación de ambos.

Este análisis podría ayudar a la empresa a identificar la oportunidad de orientación más prometedora o la siguiente mejor acción en función del valor de un cliente determinado.

Exploración rápida de datos

Echemos un vistazo rápido al conjunto de datos para poder aplicar el preprocesamiento pertinente antes de ajustar el modelo.

churn_data = read_csv('data/customer_churn.csv', show_col_types = FALSE)
# Look at the first 6 observations
head(churn_data)
# Check the dimension
dim(churn_data)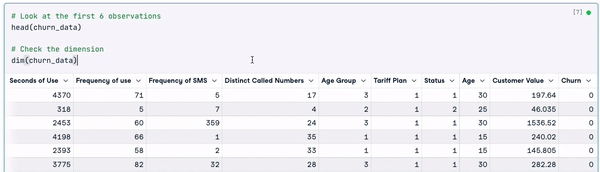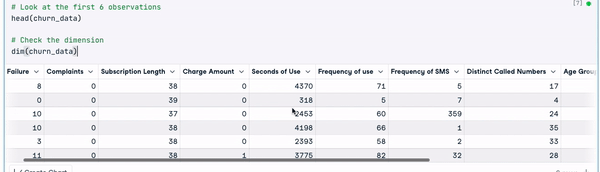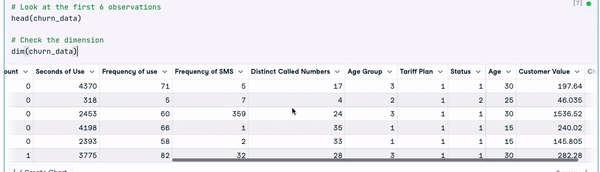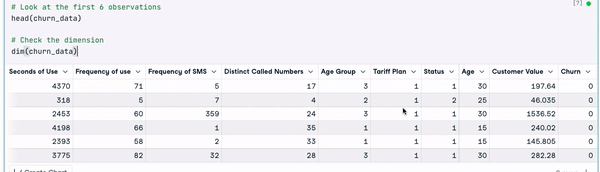

Primeras 6 filas de datos (animación del autor)

A partir de los resultados anteriores, podemos observar que el conjunto de datos tiene 3150 observaciones y 14 columnas. 

Sin embargo, al basarnos en el enunciado del problema, no necesitaremos la columna churn porque ahora nos enfrentamos a un problema de regresión.

Antes de ajustar el modelo, vamos a preprocesar los nombres de las columnas y sustituir los espacios en los nombres de las columnas por guiones bajos para evitar escribir cada vez las comillas dobles alrededor de los nombres de las variables.

# Change the column names
names(churn_data) = gsub(" ", "_", names(churn_data))

head(churn_data)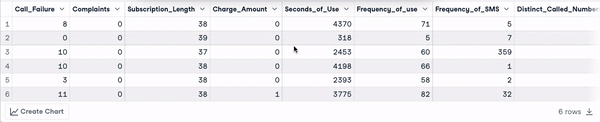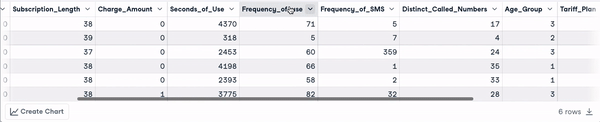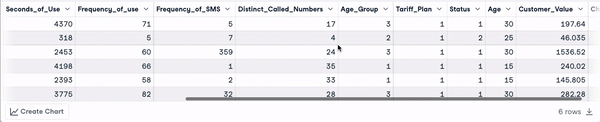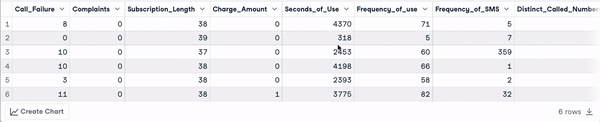

Primeras 6 filas tras la transformación de los nombres de las columnas (animación del autor)

Con estos datos recién formateados, podemos ajustarlos al marco de regresión múltiple mediante la función lm() de R de la siguiente manera:

# Fit the multiple linear regression model
cust_value_model = lm(formula = Customer_Value ~ Call_Failure + 

                     Complaints + Subscription_Length + Charge_Amount +    

                     Seconds_of_Use +Frequency_of_use + Frequency_of_SMS +
                    Distinct_Called_Numbers + Age_Group + Tariff_Plan +
                    Status + Age,data = churn_data)

Entendamos lo que acabamos de hacer aquí.

La función lm() tiene el siguiente formato: lm(formula = Y ~Sum(Xi), data = our_data)

• Y es la columna Customer_Value porque es la que intentamos estimar.
• Sum(Xi) representa la expresión de la suma en la ecuación de regresión lineal múltiple. 
• our_data is the churn_data.

Puedes obtener más información en nuestro curso Regresión intermedia en R. 

Una alternativa al uso de R es la Regresión intermedia con modelos estadísticos en Python. Ambos te ayudan a aprender la regresión lineal y logística con múltiples variables explicativas.

¿Qué nos dice el modelo de regresión lineal múltiple?

Ahora que hemos construido el modelo, el siguiente paso es comprobar los supuestos e interpretar los resultados. Para simplificar, no cubriremos todos los aspectos.

Distribución de los residuos del modelo 

Esto se puede mostrar en R mediante la función hist().

# Get the model residuals
model_residuals = cust_value_model$residuals

# Plot the result
hist(model_residuals)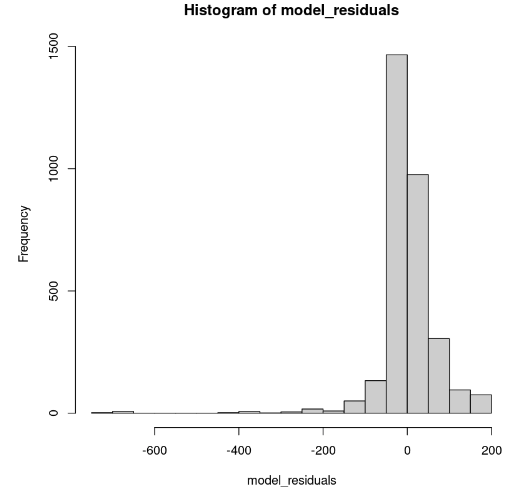

Distribución de los residuos del modelo (imagen del autor)

El histograma parece sesgado hacia la izquierda, por lo que no podemos concluir la normalidad con suficiente confianza. En lugar del histograma, veamos los residuos a lo largo del gráfico normal Q-Q. Si hay normalidad, los valores deben seguir una línea recta.

# Plot the residuals
qqnorm(model_residuals)
# Plot the Q-Q line
qqline(model_residuals)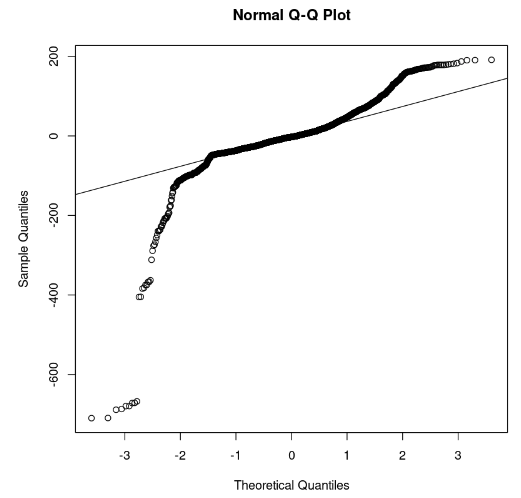

Gráfico Q-Q y residuos (imagen del autor)

En el gráfico podemos observar que algunas partes de los residuos se sitúan en una línea recta. Entonces podemos suponer que los residuos del modelo no siguen una distribución normal.  

Comprobación del supuesto de multicolinealidad 

Esto se hace mediante el siguiente código R. Pero antes tenemos que eliminar la columna Customer_Value.

# Install and load the ggcorrplot package
install.packages("ggcorrplot")
library(ggcorrplot)

# Remove the Customer Value column
reduced_data <- subset(churn_data, select = -Customer_Value)

# Compute correlation at 2 decimal places
corr_matrix = round(cor(reduced_data), 2)

# Compute and show the  result
ggcorrplot(corr_matrix, hc.order = TRUE, type = "lower",
          lab = TRUE)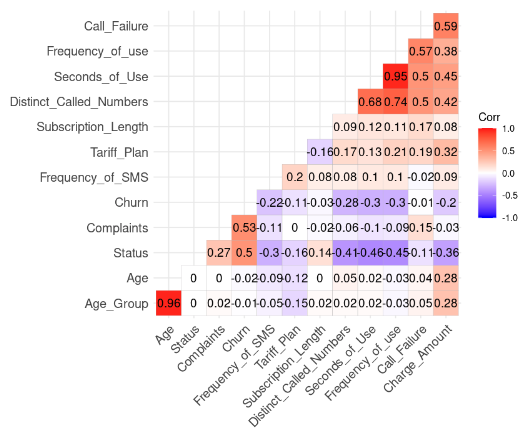

Resultado de la correlación de los datos (imagen del autor)

Podemos observar dos correlaciones fuertes porque su valor es superior a 0,8. 

• Age y Age_Group: 0,96
• Frequency_of_Use y Second_of_Use: 0,95

Este resultado tiene sentido porque Age_Group se calcula a partir de Age. Además, el número total de segundos (Second_of_Use) se obtiene a partir del número total de llamadas (Frequency_of_Use). 

En este caso, podemos deshacernos del Age_Group y del Second_of_Use en el conjunto de datos. 

Intentemos construir un segundo modelo sin esas dos variables.

second_model = lm(formula = Customer_Value ~ Call_Failure + Complaints +
                    Subscription_Length + Charge_Amount +
                    Frequency_of_use + Frequency_of_SMS +
                    Distinct_Called_Numbers + Tariff_Plan +
                    Status + Age,
                    data = churn_data)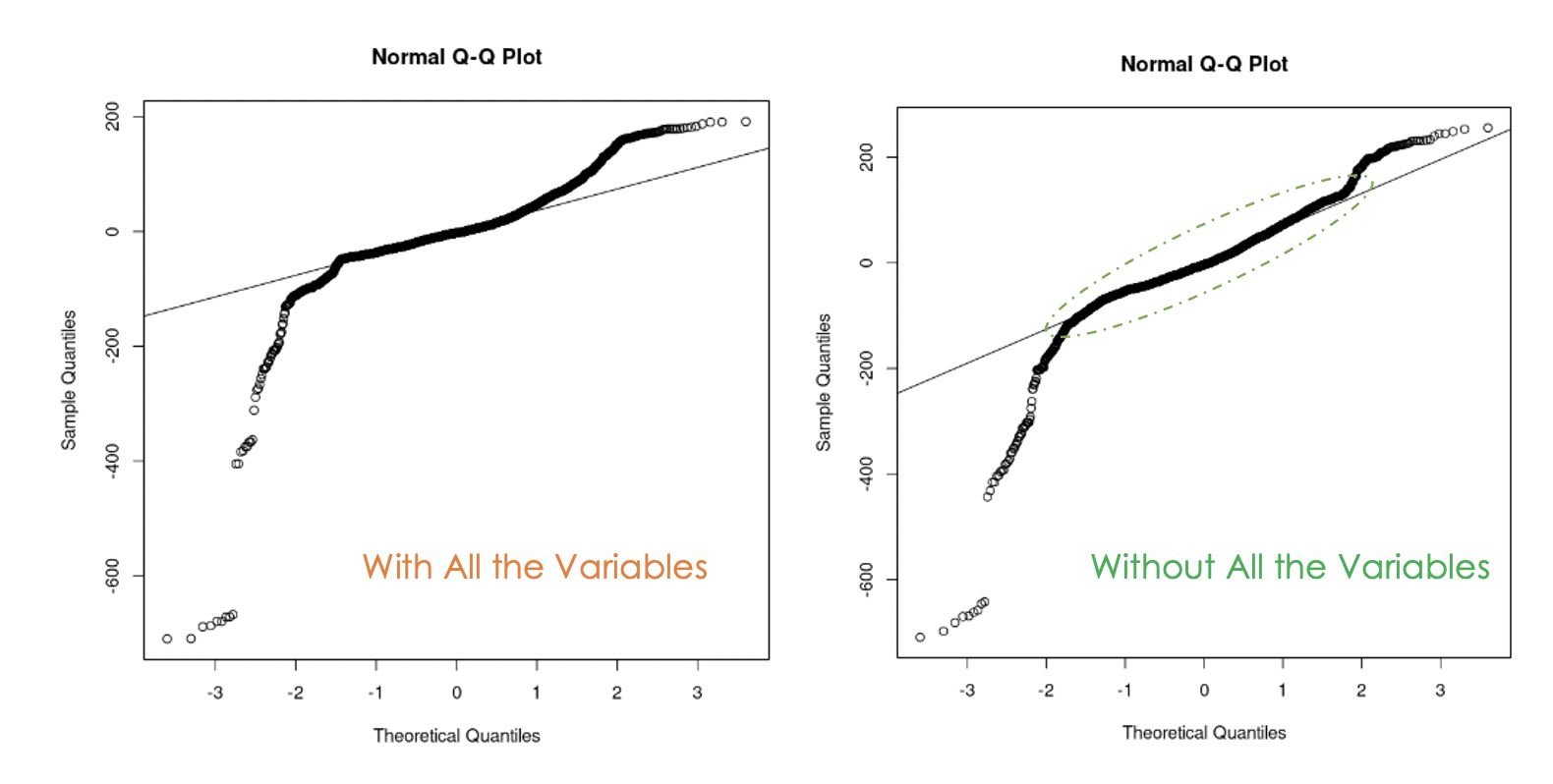

Gráficos Q-Q del primer modelo (izquierda) y del segundo modelo (derecha)

Podemos observar que deshacerse de la multicolinealidad en los datos fue útil porque, con el segundo modelo, más valores residuales están en la línea recta en comparación con el primer modelo.

¿Cómo saber cuál de los dos modelos es mejor? 

Una forma de responder a esta pregunta es realizar una prueba de análisis de la varianza (ANOVA) de los dos modelos. Contrasta la hipótesis nula(H0), según la cual las variables que eliminamos anteriormente no tienen significación, con la hipótesis alternativa(H1), según la cual esas variables son significativas. 

Si el nuevo modelo es una mejora del modelo original, entonces no rechazamos H0. Si no es así, significa que esas variables eran significativas; por tanto, rechazamos H0. 

He aquí la expresión general: anova(original_model, new_model)

# Anova test
anova(cust_value_model, second_model)

Resultado de la prueba ANOVA (imagen del autor)

A partir del resultado del ANOVA, observamos que el valor p (8,0893e-316) es muy pequeño (inferior a 0,05), por lo que rechazamos la hipótesis nula, lo que significa que el segundo modelo no es una mejora del primero. 

Otra forma de ver las variables importantes del modelo es mediante una prueba de significación. 

Una variable será significativa si su valor p es inferior a 0,05. Este resultado puede generarse mediante la función summary(). Además de proporcionar esa información sobre el modelo, también muestra el R cuadrado ajustado, que evalúa el rendimiento de los modelos entre sí.

# Print the result of the model
summary(cust_value_model)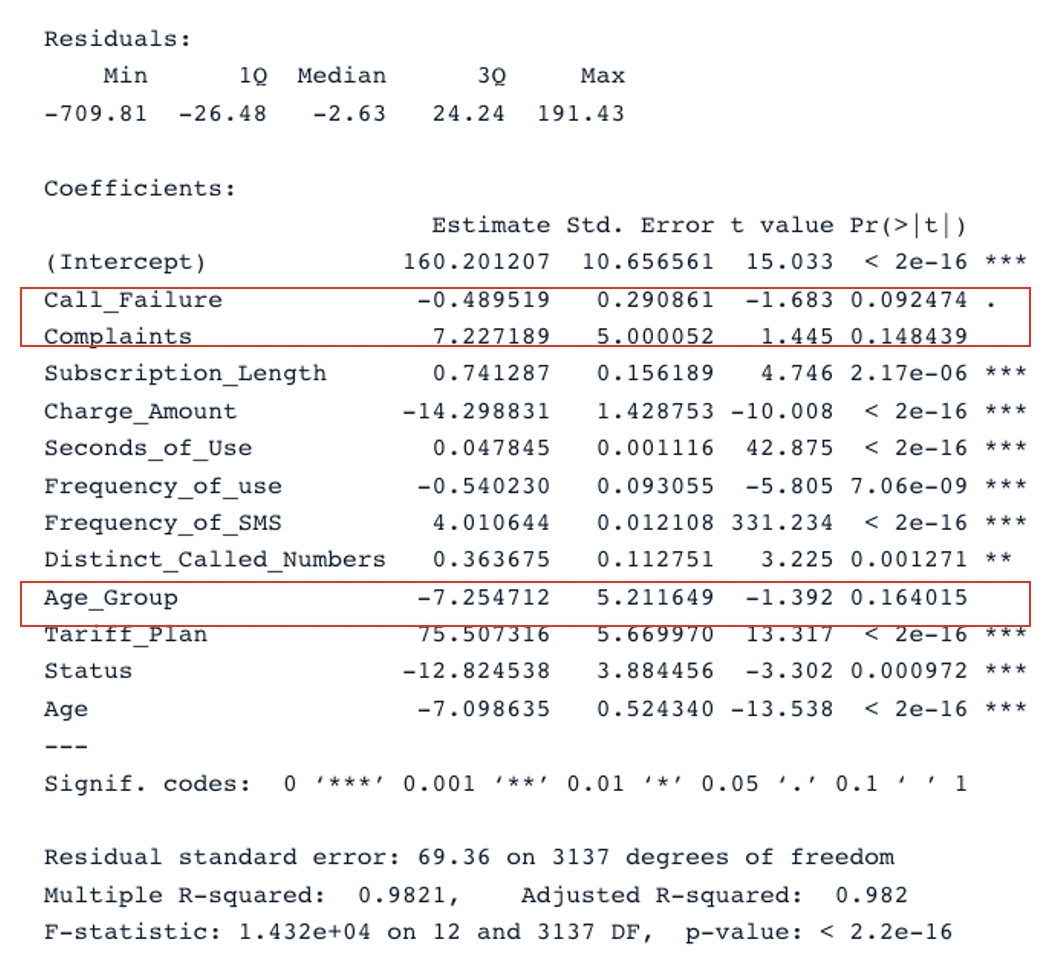

Resultado resumido del modelo original con todos los predictores (imagen del autor)

Tenemos dos secciones clave en la tabla: Residuals y Coefficients. Los gráficos Q-Q ofrecen la misma información que la sección Residuals. En la sección Coefficients, Call_Failure, Complaints y Age_Group no se consideran significativos por el modelo porque su valor p es superior a 0,05. Conservarlos no aporta ningún valor adicional al modelo.

Aplicando el mismo análisis al segundo modelo, obtenemos este resultado:

summary(second_model)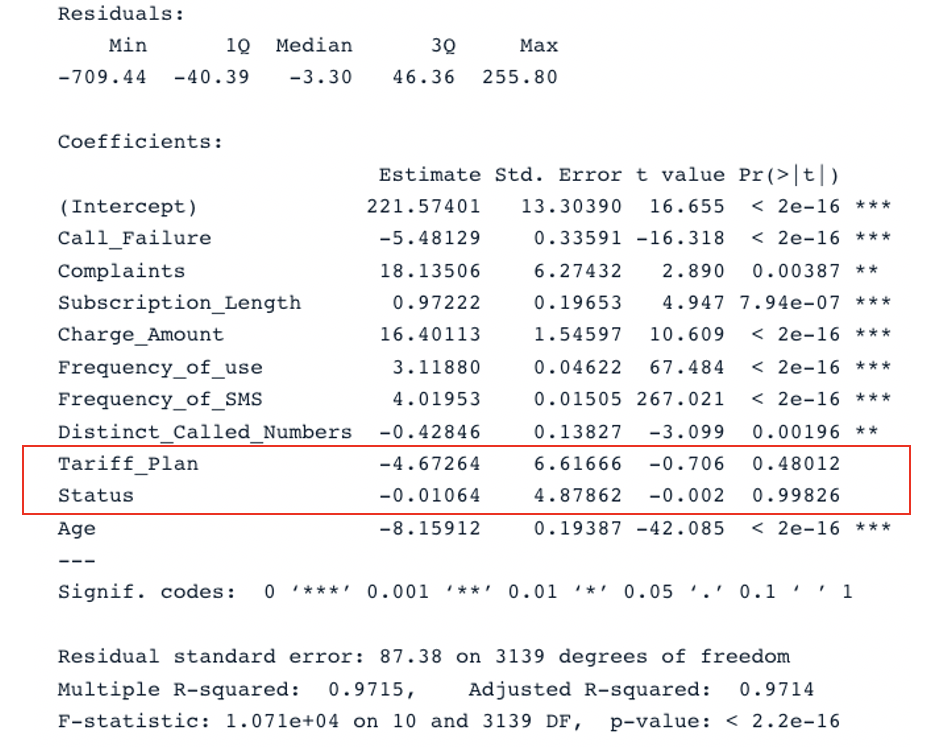

Resultado resumido del segundo modelo con todos los predictores (imagen del autor)

El modelo original tiene un R cuadrado ajustado de 0,98, que es superior al R cuadrado ajustado del segundo modelo (0,97). Esto significa que el modelo original con todos los predictores es mejor que el segundo modelo.

Mejorar el modelo de regresión lineal múltiple

El siguiente paso lógico de este análisis es eliminar las variables no significativas y ajustar el modelo para ver si mejora el rendimiento.

Otra estrategia para elegir eficazmente los predictores relevantes es mediante el Criterio de Información de Akaike (AIC). 

Empieza con todas las características y, a continuación, elimina gradualmente los peores predictores de uno en uno hasta encontrar el mejor modelo. Cuanto menor sea la puntuación AIC, mejor será el modelo. Esto puede hacerse utilizando la función stepAIC().

Conclusión

En este tutorial se han tratado los principales aspectos de las regresiones lineales múltiples y se han explorado algunas estrategias para construir modelos robustos. 

Esperamos que este tutorial te proporcione los conocimientos necesarios para obtener información procesable de tus datos. Puedes intentar mejorar estos modelos aplicando distintos enfoques utilizando el código fuente disponible en nuestro espacio de trabajo.