Matriz de correlaciones en Excel: Guía completa para crear e interpretar

La disponibilidad de las funciones incorporadas y los complementos de Excel significa que ahora es posible realizar en Excel incluso los análisis más avanzados. Como profesional principiante de la ciencia de datos, familiarizarse con Excel para diversas técnicas analíticas se ha convertido en algo crucial.

Este tutorial introducirá el concepto estadístico de correlación, sus diferentes tipos y sus aplicaciones. Tras introducir las funciones incorporadas y los complementos pertinentes, tomaremos datos de muestra para crear, visualizar e interpretar la matriz de correlaciones de Excel.

¿Qué es una Matriz de Correlaciones?

La correlación es una medida estadística que describe en qué medida dos o más variables están relacionadas entre sí. Indica la fuerza y la dirección de una relación entre variables.

Cuando las variables están correlacionadas, significa que los cambios en una variable están asociados a los cambios en otra, ya sea positiva o negativamente:

• Correlación positiva: Cuando dos variables aumentan o disminuyen juntas, están correlacionadas positivamente. Por ejemplo, la estatura y el peso suelen estar correlacionados positivamente; a medida que aumenta la estatura, el peso tiende a aumentar también.
• Correlación negativa: Cuando una variable aumenta mientras la otra disminuye. Por ejemplo, la velocidad a la que circula un vehículo y el tiempo que tarda en llegar a un destino; a medida que aumenta la velocidad, disminuye el tiempo empleado.

Los coeficientes de correlación son medidas numéricas que cuantifican la fuerza y la dirección de esta relación. Este grado de correlación puede medirse mediante distintas herramientas estadísticas, siendo el coeficiente de correlación de Pearson la más habitual.

Comprender el coeficiente de Pearson

El coeficiente de correlación de Pearson, a menudo denominado simplemente "r de Pearson", es una medida de la correlación lineal entre dos variables 𝑋 y 𝑌. Cuantifica el grado en que una relación entre estas variables puede describirse mediante una línea recta.

El coeficiente de correlación de Pearson se calcula como la covarianza de las dos variables dividida por el producto de sus desviaciones típicas. Matemáticamente, se expresa como:

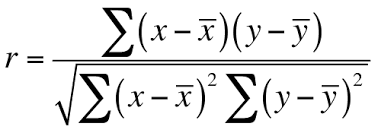
Observa que 𝑋‾y 𝑌‾ son las medias de las variables 𝑋 y 𝑌, respectivamente.

El valor del coeficiente calculado oscilará entre -1 y +1, donde:

• +1 indica una relación lineal positiva perfecta: A medida que aumenta una variable, la otra aumenta de forma perfectamente lineal.
• -1 indica una relación lineal negativa perfecta: A medida que una variable aumenta, la otra disminuye de forma perfectamente lineal.
• 0 indica que no hay correlación lineal: No existe una relación lineal entre las variables.

Visualmente, así es como se verán los distintos tipos de correlaciones:

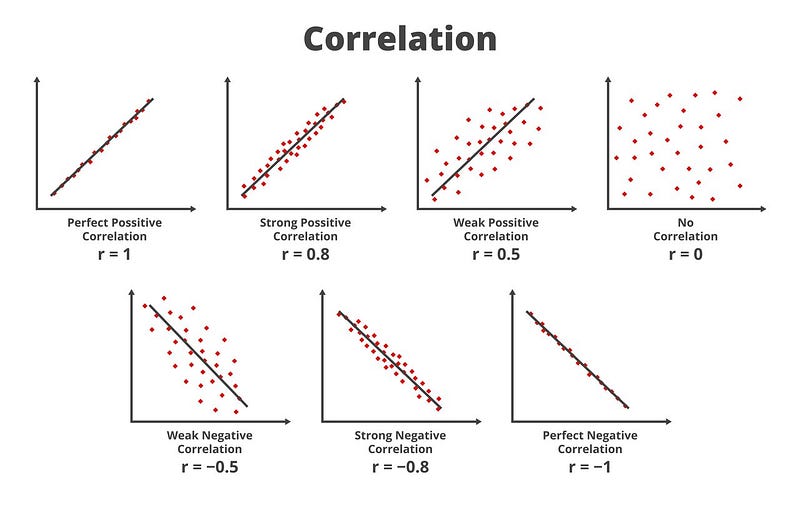Representación visual de las correlacionesRepresentación de las correlaciones(Fuente)

Ahora que hemos comprendido términos como correlación y coeficientes de correlación, vamos a entender cómo se reúne todo en una matriz de correlaciones.

Una matriz de correlaciones es una tabla que muestra los coeficientes de correlación entre múltiples variables. Cada celda de la matriz representa la correlación entre dos variables.

Esta matriz es una herramienta útil para analizar la fuerza y la dirección de las relaciones entre variables en el análisis estadístico de datos. Más allá de este uso obvio de la matriz de correlaciones, se utiliza para diversas aplicaciones en ciencia de datos, finanzas, estudios de mercado, etc.

Algunas de estas aplicaciones son:

• En la ciencia de datos, la utilizamos para seleccionar o excluir características (variables) de los modelos basándonos en sus relaciones. Los rasgos muy correlacionados pueden causar multicolinealidad en los modelos de regresión, lo que podría sesgar los resultados. Al identificar estas correlaciones, reducimos la redundancia y mejoramos el rendimiento del modelo.
• En finanzas, las matrices de correlación se utilizan para comprender cómo se mueven los distintos activos entre sí. Esto es crucial para la diversificación de la cartera y la gestión del riesgo, ya que ayuda a seleccionar activos que no estén fuertemente correlacionados, reduciendo así potencialmente el riesgo.
• Las empresas utilizan matrices de correlación para encontrar relaciones entre distintos comportamientos de los consumidores, valoraciones de productos y variables demográficas. Esto ayuda a mejorar la orientación y el posicionamiento de los productos. Veremos un ejemplo similar más adelante en este tutorial.

Ahora que hemos comprendido el concepto de correlación, sus cálculos y sus aplicaciones, vamos a sumergirnos en su aplicación en Excel.

Matriz de correlaciones: Funciones y complementos relevantes en Excel

Dos herramientas que utilizaremos para calcular matrices de correlación en Excel son la función CORREL y el complemento Analysis ToolPak.

Función CORREL

La función CORREL de Excel proporciona un método sencillo para calcular el coeficiente de correlación de Pearson entre dos conjuntos de datos.

La sintaxis de la función CORREL es:

CORREL(array1, array2)

donde:

• array1: Es el rango de celdas que contiene el primer conjunto de datos/columna.
• array2: Es el rango de celdas que contiene el segundo conjunto de datos/columna.

Cada matriz debe tener el mismo número de elementos. Excel te devolverá el coeficiente de correlación de estas matrices, que oscila entre -1 y +1.

Analysis ToolPak

Para un análisis estadístico más exhaustivo, que incluya la generación de una matriz de correlación completa entre varias variables, puede ser útil el paquete de herramientas de análisis de Excel.

Puede que el Paquete de Herramientas de Análisis no esté necesariamente activado en tu documento Excel. Comprueba si el icono "Análisis de datos" está visible en la esquina derecha, debajo de la pestaña "Datos", como se muestra a continuación.

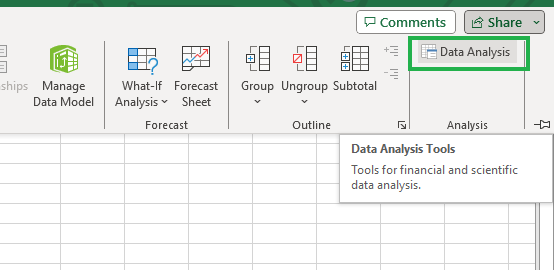
Conjunto de herramientas de análisis en Excel.

Si no puedes verlo, no te preocupes; sigue los pasos que se indican a continuación y podrás activar el Paquete de herramientas de análisis.

• Haz clic en File en el menú, y luego selecciona Options.

Seleccionando Opciones en la pestaña Archivo.

• En el cuadro de diálogo Excel Options, selecciona Add-ins.

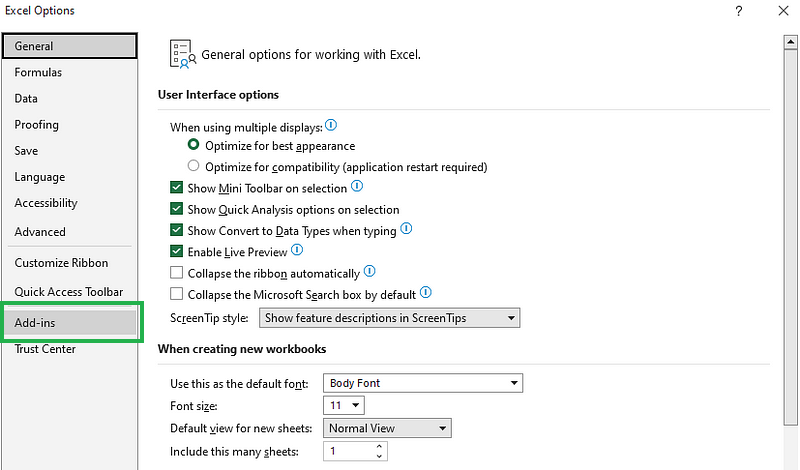
Selecciona Complementos en el cuadro de diálogo Opciones de Excel.

• En el cuadro Manage de la parte inferior de la vista, selecciona Excel Add-ins y haz clic en Go.

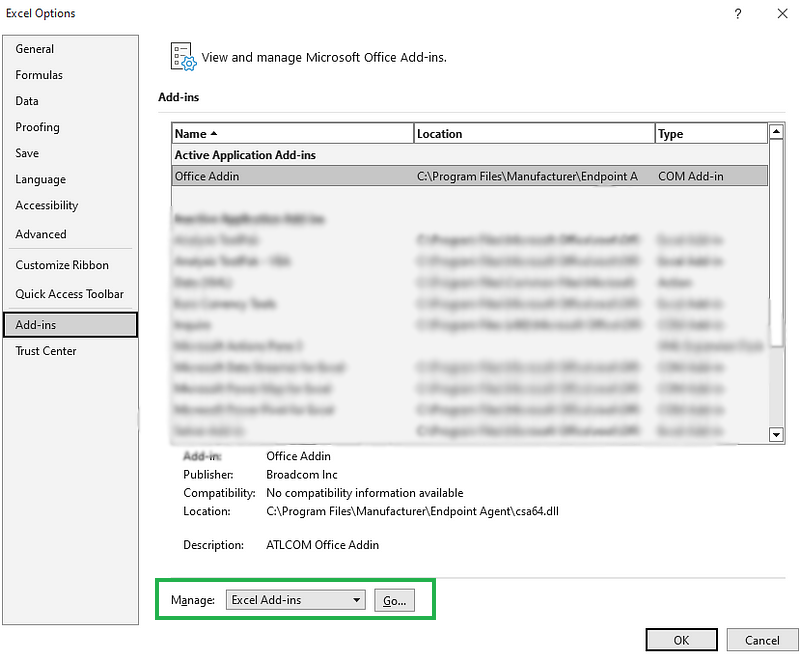
Gestionar complementos de Excel.

• En la casilla Add-Ins, marca Analysis ToolPak y luego haz clic en OK.

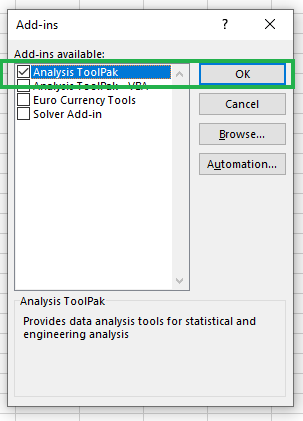
Habilitación del Conjunto de Herramientas de Análisis.

Deberías poder ver el icono "Análisis de datos" en la pestaña Data, en el grupo Analysis, si has seguido las instrucciones y lo has activado correctamente.

Como verás más adelante, Analysis ToolPak hace que el proceso de cálculo de la matriz de correlaciones sea mucho más fácil y sencillo.

Cómo crear una matriz de correlaciones en Excel: Un ejemplo

Considera un escenario en el que eres analista de datos en una empresa líder de bienes de consumo con múltiples tiendas en todo el país. La empresa ha recopilado datos sobre ventas y demografía de los clientes.

Tu objetivo es comprender las relaciones entre las características de los clientes y sus pautas de compra. Este análisis tratará de encontrar productos que se compren habitualmente juntos y explorar cómo influyen diversos factores demográficos en las tendencias de venta.

Has decidido utilizar una matriz de correlaciones para el análisis. Se te han proporcionado los siguientes datos de muestra de 10 clientes en un archivo Excel:

Datos de muestra de una empresa líder en bienes de consumo.

Las columnas son:

• ID de cliente: Identificador único para cada cliente.
• La edad: Edad del cliente en años.
• Ingresos anuales (K$): Los ingresos anuales del cliente en miles de dólares.
• Frecuencia de visitas (al mes): Con qué frecuencia visita el cliente la tienda cada mes.
• Gasto por visita ($): Cantidad media de dinero gastada por el cliente en cada visita a la tienda.
• Electrónica ($) / Ropa ($) / Comestibles ($): Cantidad gastada en diferentes categorías de productos por visita.

Correlaciones manuales mediante la función CORREL

Aquí tienes los pasos a seguir para calcular el coeficiente de correlación de Pearson en Excel:

• Paso 1: Selecciona la celda adecuada que forma la parte de la matriz de correlaciones. Aquí seleccionamos, B16.

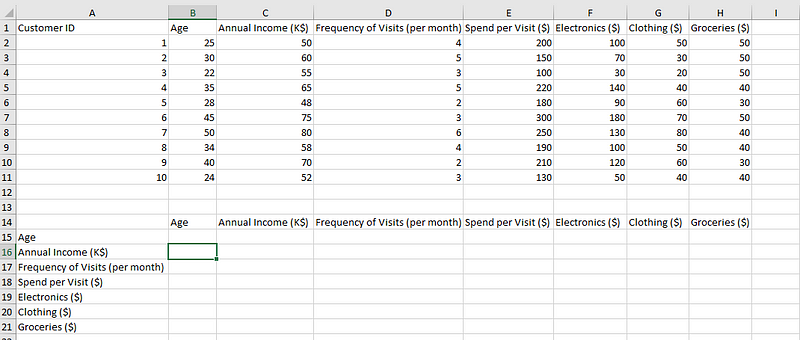
Seleccionar una celda para calcular la correlación.

• Paso 2: Escribe la siguiente fórmula que utiliza la función CORREL. Primero calcularemos la correlación entre Edad e Ingresos anuales.

=CORREL(B2:B11,C2:C11)

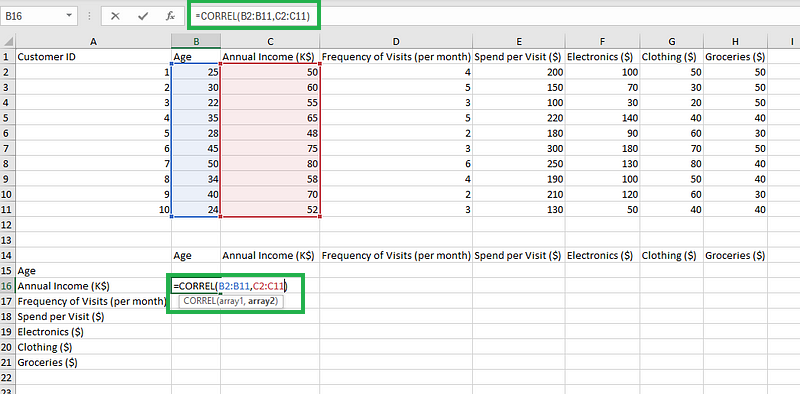
Escribe la fórmula.

• Paso 3: Introduce la celda y repite el proceso para el resto de combinaciones de columnas.

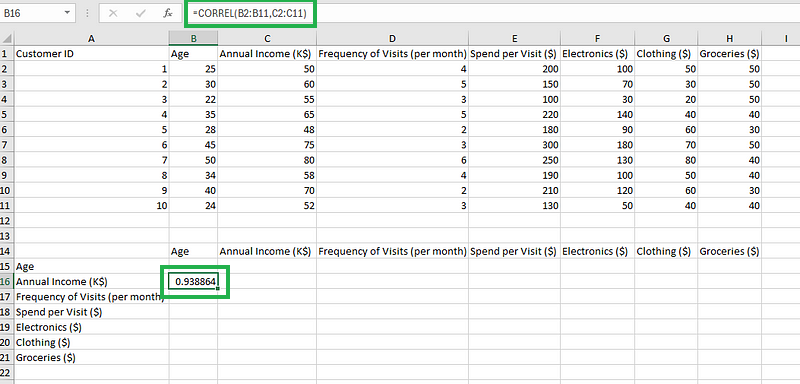
Cálculo de la correlación.

Como ves, calcular manualmente los valores de correlación para cada combinación de columnas podría resultar tedioso, sobre todo cuando aumenta el número de columnas de los datos.

También tenemos la opción de utilizar la función OFFSET para automatizar los cambios en los rangos de celdas para rellenar los valores de los coeficientes en la tabla.

Aunque es importante saber que la función CORREL existe y es útil para calcular correlaciones individuales, cuando se considera una matriz de correlaciones completa, el Paquete de Herramientas de Análisis es mucho más fácil y rápido, por lo que se recomienda.

Matriz de correlaciones mediante la herramienta de análisis

Estos son los pasos que debes seguir para crear la matriz de correlaciones:

• Paso 1: Haz clic en el icono Análisis de Datos de la pestaña Datos.

Haciendo clic en el icono Análisis de Datos.

• Paso 2: Selecciona la opción "Correlación" y haz clic en "Aceptar".

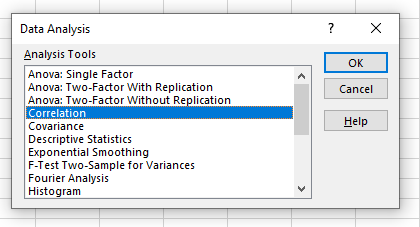
Seleccionando la opción de correlación.

• Paso 3: Proporciona el rango de entrada, incluyendo los nombres de las Columnas. Marca la opción "Etiquetas en la primera fila". Para el rango de salida, selecciona cualquier celda en la que quieras mostrar los resultados, por ejemplo $A$14, aquí. Por último, pulsa OK.

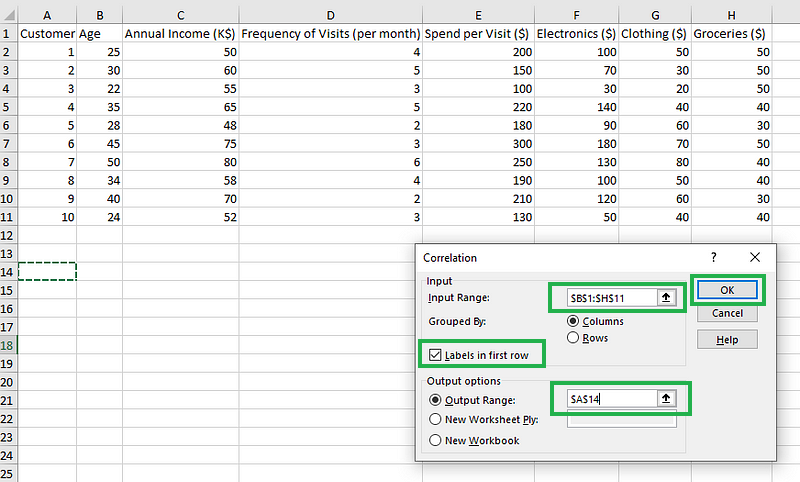
Rellenar los detalles de las correlaciones utilizando el complemento Analysis Toolpak.

Deberías poder ver la matriz de correlaciones como se muestra a continuación:

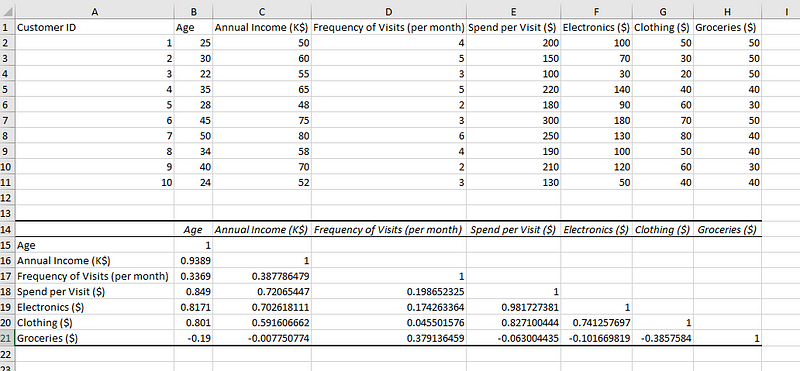
Datos con su matriz de correlaciones.

El valor de correlación de cualquier columna consigo misma es 1, lo que significa una correlación perfecta consigo misma. La matriz tiene todas las columnas presentes también en la fila, creando todas las combinaciones de columnas entre sí. La diagonal superior derecha de la matriz está vacía, ya que se parecerá exactamente a las combinaciones de la diagonal inferior izquierda.

Hemos creado con éxito la matriz de correlaciones en Excel. Ahora, es el momento de comprender lo que significan esos valores y convertir esas cifras en ideas.

Cómo interpretar una matriz de correlación en Excel

Aunque interpretar la matriz de correlaciones que vimos antes no es demasiado difícil, se nos va de las manos cuando aumenta el número de columnas. Es imposible repasar cada combinación cuando el número de columnas es elevado.

Necesitamos un mecanismo para identificar rápidamente las correlaciones más significativas entre todas las combinaciones posibles de la matriz de correlaciones.

El formato condicional de estas celdas en una matriz de correlaciones ayuda a interpretar mejor la matriz de correlaciones, dirigiendo nuestra atención a las celdas más significativas (tonos más oscuros) de la matriz de correlaciones.

He aquí los pasos para codificar por colores la matriz de correlaciones en Microsoft Excel:

• Paso 1: Resalta la matriz de correlaciones (sólo los números), y haz clic en Formato condicional en la pestaña "Inicio". Haz clic en "Nueva regla", como se muestra a continuación.

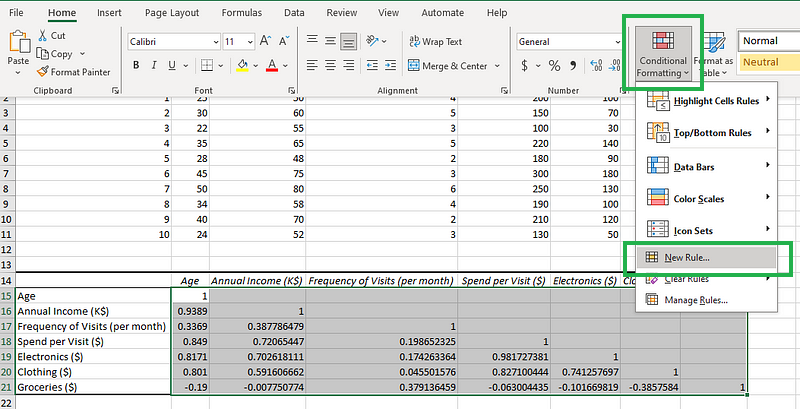
Haciendo clic en el icono "Formato condicional".

• Paso 2: Después del paso 1, deberías ver un cuadro de diálogo como el que se muestra en el diagrama siguiente. Primero, selecciona "Formatear todas las celdas en función de sus valores" y establece el estilo de formato en "Escala de 3 colores". Tres colores son ideales porque pueden denotar correlaciones positivas, negativas y neutras según corresponda. Por último, establece el Tipo, el Valor y el Color como se muestra en el diagrama siguiente.

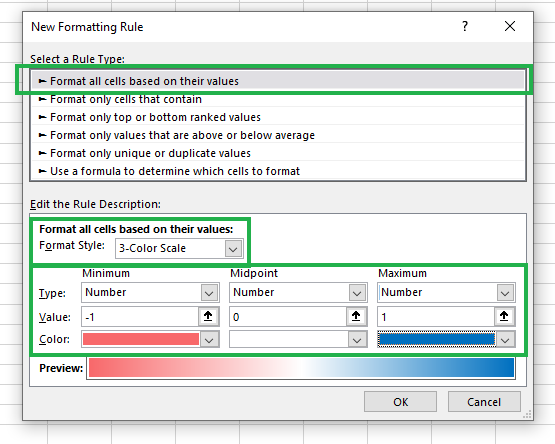
Crear una nueva regla de formato condicional.

Verás un resultado como el que se muestra a continuación:

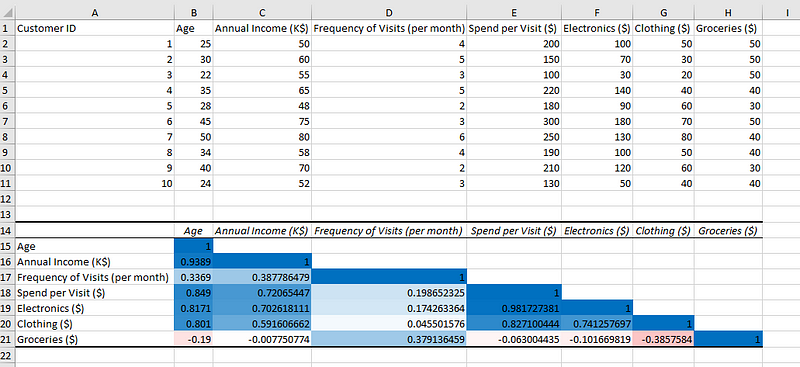
Datos de muestra, con matriz de correlación codificada por colores.

Eso es. Hemos añadido colores para visualizar mejor la matriz de correlaciones.

Una vez codificada por colores la matriz de correlaciones para su comprensión visual, podemos deducir lo siguiente de los resultados obtenidos:

• La edad está fuertemente correlacionada de forma positiva con los ingresos anuales, lo que significa que cuanto mayores son los clientes, mayor es su poder adquisitivo.
• La cantidad gastada en comestibles está correlacionada negativamente con todas las variables excepto con la frecuencia de visitas de los clientes, que está correlacionada positivamente, lo que significa que es probable que los clientes compren más comestibles cuando visitan más la tienda.
• Las categorías de ropa y aparatos electrónicos tienen una fuerte correlación positiva, por lo que puede ser una buena idea tener cerca estas dos categorías de artículos para aumentar las ventas.
• Las categorías de ropa y comestibles tienen una correlación negativa, lo que significa que es mejor no tener estas categorías cerca en las tiendas físicas.

La clave para interpretar la matriz de correlaciones es observar la dirección y la fuerza del valor en la matriz y retroceder hasta las columnas asociadas a él.

Observa que, en nuestras explicaciones, nunca hemos afirmado que los clientes de más edad obtengan ingresos anuales más elevados debido a su mayor edad, ni que las mayores ventas de ropa provoquen menores ventas de comestibles. Esto se debe a que, correlación no es causalidad, un error popular.

Sólo podemos interpretar la existencia (o inexistencia) de una relación entre dos variables, pero nunca que una variable esté provocando un cambio en la otra variable, mediante un análisis correlacional. Para determinar una relación de causalidad, necesitamos realizar experimentos específicos, y puedes aprender más sobre ello en nuestra Correlación vs. Causalidad. Tutorial de causalidad.

Reflexiones finales

Este tutorial introduce el concepto de correlación, el coeficiente de Pearson, su expresión matemática, los distintos tipos de correlaciones y cómo identificarlas en función de la dirección y la fuerza de los coeficientes de correlación.

A continuación, cambiamos nuestro enfoque hacia la aplicación, donde tomamos datos de muestra, creamos, visualizamos con formato condicional e interpretamos la matriz de correlaciones. También nos fijamos en los conceptos erróneos a la hora de interpretar la matriz de correlaciones.

¡Tu aprendizaje no tiene por qué acabar aquí! Si estás interesado en implementar correlaciones utilizando otros lenguajes de programación, las siguientes guías te serán de utilidad:

• Tutorial de Correlación en R
• Tutorial de correlación en Python
• SQL Correlation Course

Para consolidar tus conocimientos técnicos relacionados, consulta nuestros cursos de Probabilidad y Estadística para principiantes. Alternativamente, si te sientes seguro con los conceptos técnicos pero quieres mejorar tus habilidades de aplicación práctica en Excel, deberías consultar el curso de Fundamentos de Excel.