Matriz de correlação no Excel: Um guia completo para criar e interpretar

A disponibilidade das funções integradas e dos suplementos do Excel significa que até mesmo as análises mais avançadas agora são possíveis no Excel. Como um profissional iniciante em ciência de dados, é fundamental que você se familiarize com o Excel para várias técnicas de análise.

Este tutorial apresentará o conceito estatístico de correlação, seus diferentes tipos e suas aplicações. Depois de apresentar as funções internas e os suplementos relevantes, usaremos dados de amostra para criar, visualizar e interpretar a matriz de correlação do Excel.

O que é uma matriz de correlação?

A correlação é uma medida estatística que descreve o grau em que duas ou mais variáveis estão relacionadas entre si. Indica a força e a direção de um relacionamento entre variáveis.

Quando as variáveis estão correlacionadas, isso significa que as alterações em uma variável estão associadas a alterações em outra, seja positiva ou negativamente:

• Correlação positiva: Quando duas variáveis aumentam ou diminuem juntas, elas estão positivamente correlacionadas. Por exemplo, a altura e o peso são normalmente correlacionados positivamente; à medida que a altura aumenta, o peso tende a aumentar também.
• Correlação negativa: Quando uma variável aumenta e a outra diminui. Por exemplo, a velocidade com que um veículo viaja e o tempo que leva para chegar a um destino; à medida que a velocidade aumenta, o tempo gasto diminui.

Os coeficientes de correlação são medidas numéricas que quantificam a força e a direção dessa relação. Esse grau de correlação pode ser medido usando diferentes ferramentas estatísticas, sendo o coeficiente de correlação de Pearson o mais comum.

Entendendo o coeficiente de Pearson

O coeficiente de correlação de Pearson, geralmente chamado simplesmente de "r de Pearson", é uma medida da correlação linear entre duas variáveis 𝑋 e 𝑌. Ele quantifica o grau em que uma relação entre essas variáveis pode ser descrita por meio de uma linha reta.

O coeficiente de correlação de Pearson é calculado como a covariância das duas variáveis dividida pelo produto de seus desvios padrão. Matematicamente, isso é expresso como:

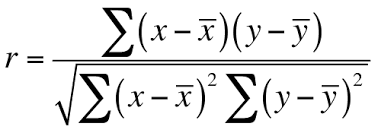
Observe que 𝑋‾e 𝑌‾ são as médias das variáveis 𝑋 e 𝑌, respectivamente.

O valor do coeficiente calculado varia de -1 a +1, sendo que:

• +1 indica uma relação linear positiva perfeita: À medida que uma variável aumenta, a outra variável aumenta de forma perfeitamente linear.
• -1 indica uma relação linear negativa perfeita: À medida que uma variável aumenta, a outra variável diminui de forma perfeitamente linear.
• 0 indica que não há correlação linear: Não há relação linear entre as variáveis.

Visualmente, você verá como os diferentes tipos de correlações se parecerão:

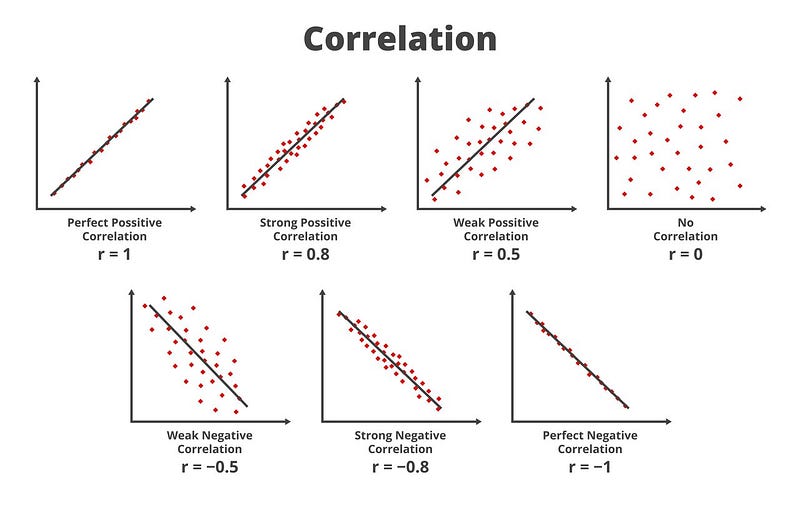Representação das correlações(Fonte)

Agora que você já entendeu termos como correlação e coeficientes de correlação, vamos entender como tudo isso se resume em uma matriz de correlação.

Uma matriz de correlação é uma tabela que exibe os coeficientes de correlação entre várias variáveis. Cada célula da matriz representa a correlação entre duas variáveis.

Essa matriz é uma ferramenta útil para analisar a força e a direção das relações entre as variáveis na análise de dados estatísticos. Além desse uso óbvio da matriz de correlação, ela é usada para várias aplicações em ciência de dados, finanças, pesquisa de mercado e muito mais.

Alguns desses aplicativos são:

• Na ciência de dados, usamos esse recurso para selecionar ou excluir recursos (variáveis) de modelos com base em seus relacionamentos. Recursos altamente correlacionados podem causar multicolinearidade nos modelos de regressão, o que pode distorcer os resultados. Ao identificar essas correlações, reduzimos a redundância e melhoramos o desempenho do modelo.
• Em finanças, as matrizes de correlação são usadas para entender como diferentes ativos se movem em relação uns aos outros. Isso é crucial para a diversificação do portfólio e para o gerenciamento de riscos, pois ajuda a selecionar ativos que não estão fortemente correlacionados, reduzindo assim potencialmente o risco.
• As empresas usam matrizes de correlação para encontrar relações entre diferentes comportamentos do consumidor, classificações de produtos e variáveis demográficas. Isso ajuda a melhorar o direcionamento e o posicionamento dos produtos. Veremos um exemplo semelhante mais adiante neste tutorial.

Agora que você já entendeu o conceito de correlação, seus cálculos e suas aplicações, vamos nos aprofundar em sua implementação no Excel.

Matriz de correlação: Funções e suplementos relevantes no Excel

Duas ferramentas que usaremos para calcular as matrizes de correlação no Excel são a função CORREL e o suplemento Analysis ToolPak.

Função CORREL

A função CORREL no Excel fornece um método simples para calcular o coeficiente de correlação de Pearson entre dois conjuntos de dados.

A sintaxe da função CORREL é:

CORREL(array1, array2)

onde:

• array1: Esse é o intervalo de células que contém o primeiro conjunto de dados/coluna.
• array2: Esse é o intervalo de células que contém o segundo conjunto de dados/coluna.

Cada matriz deve ter o mesmo número de elementos. O Excel retornará o coeficiente de correlação para essas matrizes, que varia de -1 a +1.

Analysis ToolPak

Para uma análise estatística mais abrangente, incluindo a geração de uma matriz de correlação completa entre diversas variáveis, o Analysis ToolPak no Excel pode ser útil.

O Analysis Toolpak pode não estar necessariamente habilitado em seu documento do Excel. Verifique se o ícone "Análise de dados" está visível no canto direito da guia "Dados", conforme mostrado abaixo.

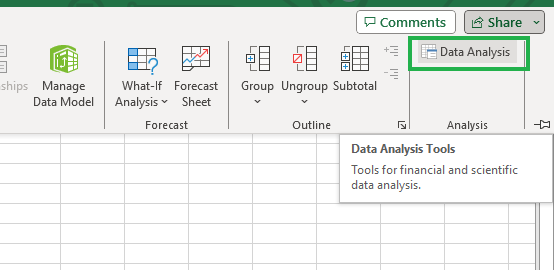
Analysis Toolpak no Excel.

Se você não conseguir visualizá-lo, não se preocupe; siga as etapas abaixo e você poderá ativar o Analysis ToolPak.

• Clique em File no menu e, em seguida, selecione Options.

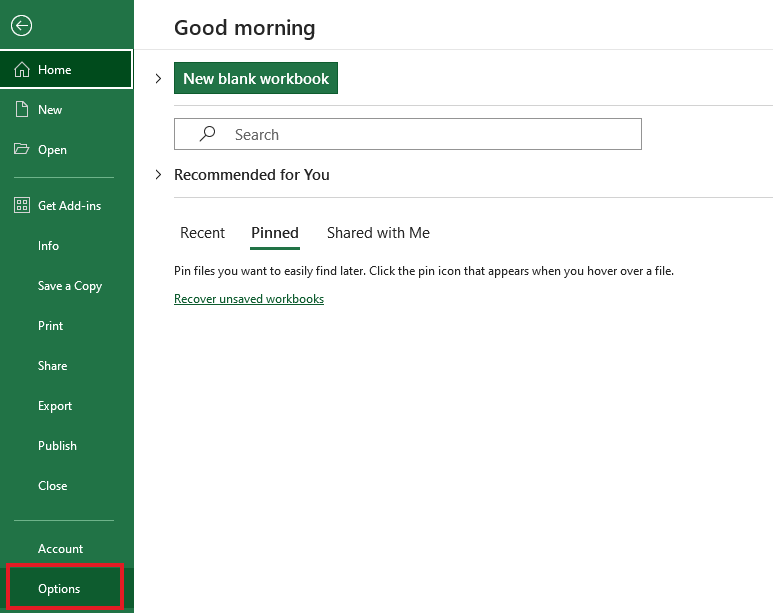
Selecionando opções na guia Arquivo.

• Na caixa de diálogo Excel Options, selecione Add-ins.

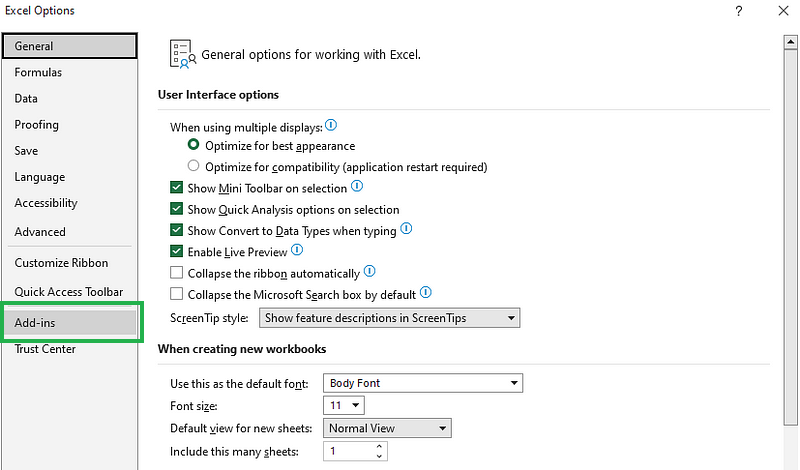
Selecione Suplementos na caixa de diálogo Opções do Excel.

• Na caixa Manage na parte inferior da visualização, selecione Excel Add-ins e clique em Go.

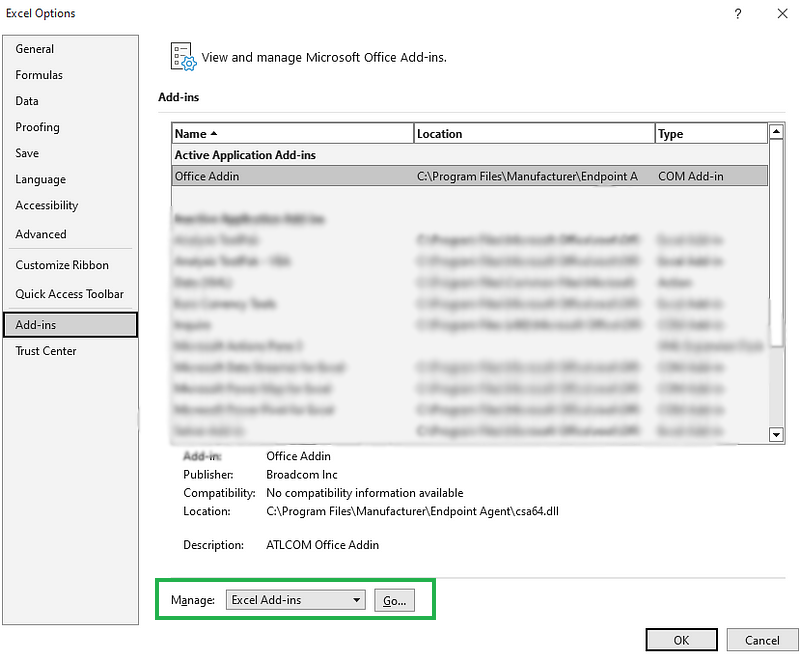
Gerenciar suplementos do Excel.

• Na caixa Add-Ins, marque Analysis ToolPak e, em seguida, clique em OK.

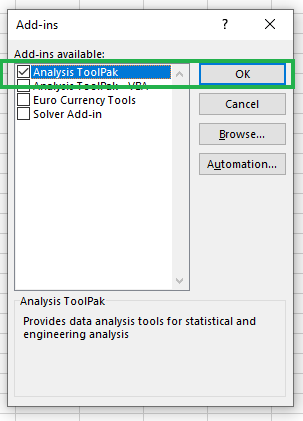
Ativação do Analysis Toolpak.

Você deverá ver o ícone "Data Analysis" na guia Data, no grupo Analysis, se tiver seguido as instruções e o ativado corretamente.

Como você verá mais adiante, o Analysis ToolPak torna o processo de cálculo da matriz de correlação muito mais fácil e direto.

Como criar uma matriz de correlação no Excel: Um exemplo

Considere um cenário em que você é um analista de dados em uma empresa líder de bens de consumo com várias lojas em todo o país. A empresa compilou dados sobre vendas e dados demográficos dos clientes.

Seu objetivo é entender as relações entre as características dos clientes e seus padrões de compra. Essa análise terá como objetivo encontrar produtos que são comumente comprados juntos e explorar como vários fatores demográficos afetam as tendências de vendas.

Você decidiu usar uma matriz de correlação para a análise. Os seguintes dados de amostra de 10 clientes foram fornecidos a você em um arquivo do Excel:

Amostra de dados de uma empresa líder em bens de consumo.

As colunas são:

• ID do cliente: Identificador exclusivo para cada cliente.
• Idade: Idade do cliente em anos.
• Renda anual (K$): A renda anual do cliente em milhares de dólares.
• Frequência de visitas (por mês): Com que frequência o cliente visita a loja a cada mês.
• Gastos por visita ($): Valor médio de dinheiro gasto pelo cliente por visita à loja.
• Eletrônicos ($) / Roupas ($) / Mercearia ($): Valor gasto em diferentes categorias de produtos por visita.

Correlações manuais usando a função CORREL

Aqui estão as etapas que você deve seguir para calcular o coeficiente de correlação de Pearson no Excel:

• Etapa 1: Selecione a célula apropriada que forma a parte da matriz de correlação. Aqui, selecionamos B16.

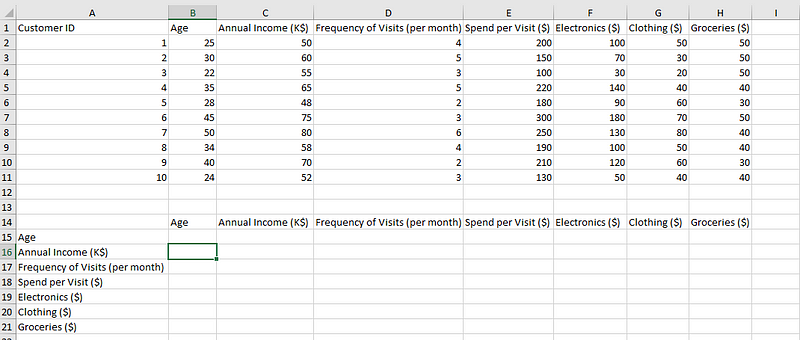
Selecionando uma célula para calcular a correlação.

• Etapa 2: Digite a seguinte fórmula que utiliza a função CORREL. Primeiro, calcularemos a correlação entre idade e renda anual.

=CORREL(B2:B11,C2:C11)

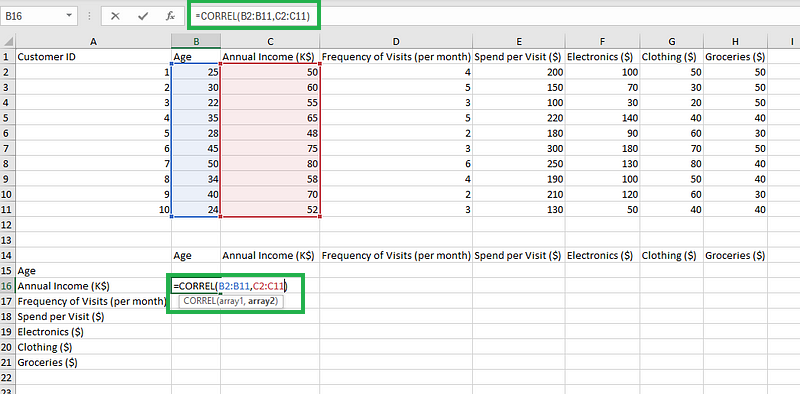
Digitando a fórmula.

• Etapa 3: Insira a célula e repita o processo para todas as outras combinações de colunas.

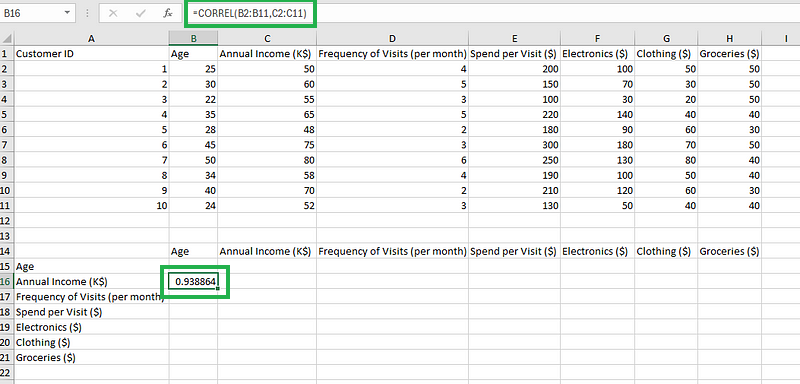
Cálculo da correlação.

Como você pode ver, calcular os valores de correlação manualmente para cada combinação de colunas pode se tornar tedioso, especialmente quando o número de colunas nos dados aumenta.

Também temos a opção de utilizar a função OFFSET para automatizar as alterações nos intervalos de células para preencher os valores de coeficiente na tabela.

Embora seja importante que você saiba que a função CORREL existe e é útil para calcular correlações individuais, ao considerar uma matriz de correlação inteira, o Analysis Toolpak é muito mais fácil e rápido, por isso é recomendado.

Matriz de correlação usando o Analysis Toolpak

Aqui estão as etapas que você deve seguir para criar a matriz de correlação:

• Etapa 1: Clique no ícone Análise de dados na guia Dados.

Clicando no ícone Análise de dados.

• Etapa 2: Selecione a opção "Correlation" (Correlação) e clique em "OK".

Selecionando a opção de correlação.

• Etapa 3: Forneça o intervalo de entrada, incluindo os nomes das colunas. Marque a opção "Rótulos na primeira linha". Para o intervalo de saída, selecione qualquer célula em que você queira exibir os resultados, como $A$14, aqui. Por fim, pressione OK.

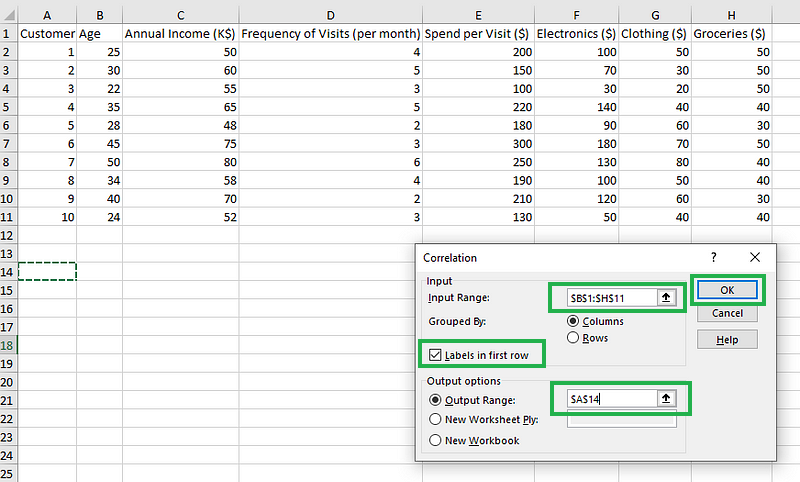
Preenchendo os detalhes das correlações usando o suplemento Analysis Toolpak.

Você poderá ver a matriz de correlação conforme mostrado abaixo:

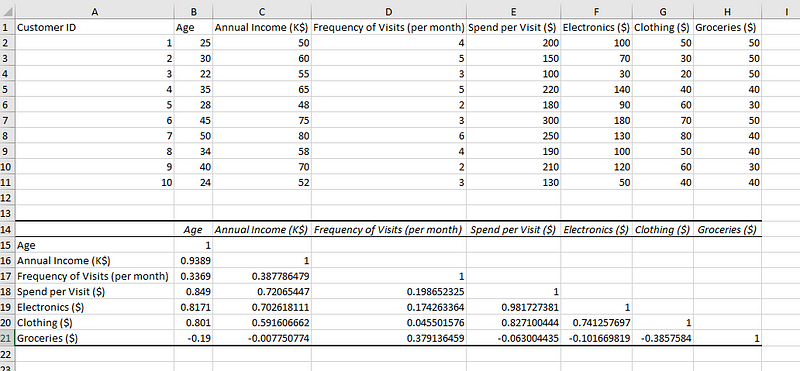
Dados com sua matriz de correlação.

O valor da correlação de qualquer coluna com ela mesma é 1, o que significa uma correlação perfeita com ela mesma. A matriz também tem todas as colunas presentes na linha, criando todas as combinações de colunas entre si. A diagonal superior direita da matriz está vazia, pois ela se assemelhará exatamente às combinações da diagonal inferior esquerda.

Criamos com sucesso a matriz de correlação no Excel. Agora, é hora de entender o que esses valores significam e converter esses números em insights.

Como interpretar uma matriz de correlação no Excel

Embora a interpretação da matriz de correlação que vimos acima não seja muito difícil, ela fica fora de controle quando o número de colunas aumenta. É impossível passar por todas as combinações quando o número de colunas é alto.

Precisamos de um mecanismo para identificar rapidamente as correlações mais significativas em meio a todas as combinações possíveis na matriz de correlação.

A formatação condicional dessas células em uma matriz de correlação ajuda a interpretar melhor a matriz de correlação, direcionando nosso foco para as células mais significativas (tons mais escuros) na matriz de correlação.

Aqui estão as etapas para você codificar por cores a matriz de correlação no Microsoft Excel:

• Etapa 1: Destaque a matriz de correlação (somente os números) e clique em Formatação condicional na guia "Home". Clique em "New Rule" (Nova regra), conforme mostrado abaixo.

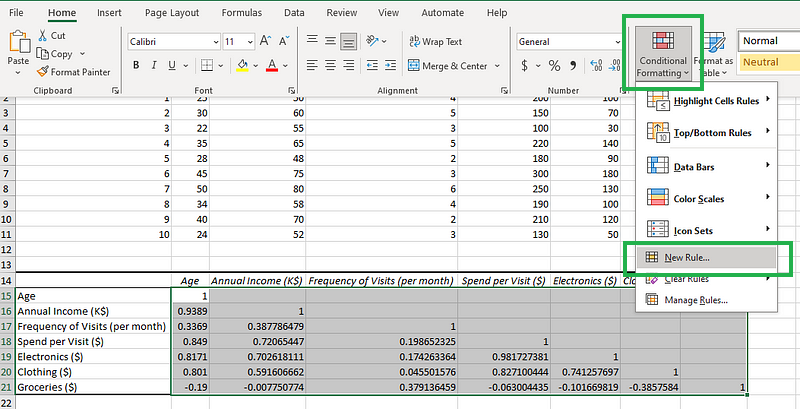
Clicar no ícone "Formatação condicional".

• Etapa 2: Após a etapa 1, você deverá ver uma caixa de diálogo como a mostrada no diagrama abaixo. Primeiro, selecione "Formatar todas as células com base em seus valores" e defina o estilo de formatação como "Escala de 3 cores". Três cores são ideais porque podem denotar correlações positivas, negativas e neutras de acordo. Por fim, defina o Tipo, o Valor e a Cor, conforme mostrado no diagrama abaixo.

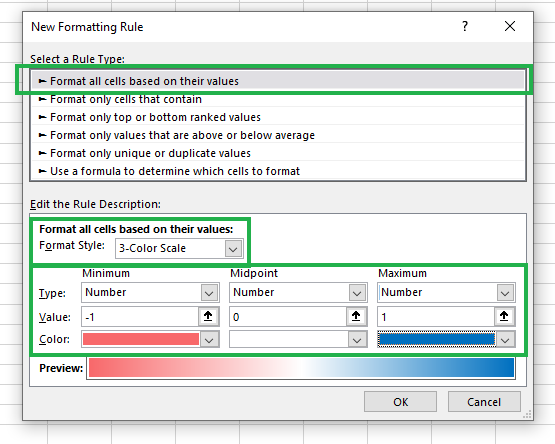
Criando uma nova regra de formatação condicional.

Você verá um resultado como o mostrado abaixo:

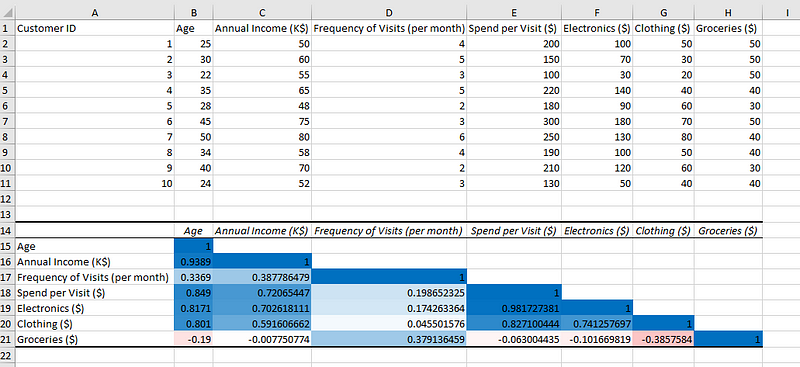
Dados de amostra, com matriz de correlação codificada por cores.

É isso aí! Adicionamos cores para que você possa visualizar melhor a matriz de correlação.

Depois de codificar a matriz de correlação por cores para compreensão visual, podemos inferir o seguinte a partir dos resultados que obtivemos:

• A idade está fortemente correlacionada de forma positiva com a renda anual, o que significa que quanto mais velhos forem os clientes, maior será seu poder de compra.
• O valor gasto em mantimentos está negativamente correlacionado com todas as variáveis, exceto com a frequência de visitas dos clientes, que está positivamente correlacionada, o que significa que os clientes provavelmente comprarão mais mantimentos quando visitarem mais a loja.
• As categorias de roupas e aparelhos eletrônicos têm uma forte correlação positiva, portanto, pode ser uma boa ideia manter essas duas categorias de itens próximas para aumentar as vendas.
• As categorias de roupas e mantimentos têm uma correlação negativa, o que significa que é melhor não manter essas categorias próximas nas lojas físicas.

O segredo para interpretar a matriz de correlação é observar a direção e a força do valor na matriz e voltar às colunas associadas a ele.

Observe que, em nossas explicações, nunca afirmamos que os clientes mais velhos recebem uma renda anual mais alta devido à sua idade mais avançada ou que as vendas mais altas de roupas causarão vendas mais baixas de mantimentos. Isso ocorre porque correlação não é causalidade, um equívoco popular.

Só podemos interpretar a existência (ou não) de uma relação entre duas variáveis, mas nunca que uma variável está causando uma mudança na outra variável, por meio de uma análise correlacional. Para determinar uma relação de causa e efeito, precisamos realizar experimentos específicos, e você pode saber mais sobre isso em em Correlação vs. Tutorial de causalidade.

Considerações finais

Este tutorial apresentou o conceito de correlação, o coeficiente de Pearson, sua expressão matemática, diferentes tipos de correlações e como identificá-las com base na direção e na força dos coeficientes de correlação.

Em seguida, mudamos nosso foco para a implementação, onde pegamos dados de amostra, criamos, visualizamos com formatação condicional e interpretamos a matriz de correlação. Também analisamos as concepções errôneas ao interpretar a matriz de correlação.

Seu aprendizado não precisa terminar aqui! Se você estiver interessado em implementar correlações usando outras linguagens de programação, os guias a seguir serão úteis:

• Tutorial de correlação do R
• Tutorial de correlação do Python
• Curso de Correlação de SQL

Para solidificar seu conhecimento técnico relacionado, confira nossos cursos de Probabilidade e Estatística para iniciantes. Como alternativa, se você se sente confiante com os conceitos técnicos, mas deseja aprimorar suas habilidades de implementação prática no Excel, deve conferir o programa Excel Fundamentals.