Korrelationsmatrix in Excel: Ein kompletter Leitfaden zum Erstellen und Interpretieren

Die Verfügbarkeit der in Excel integrierten Funktionen und Add-ins bedeutet, dass selbst die fortschrittlichsten Analysen jetzt in Excel möglich sind. Als Anfänger in der Datenwissenschaft ist es wichtig, sich mit Excel für verschiedene Analysetechniken vertraut zu machen.

In diesem Tutorium wird das statistische Konzept der Korrelation, seine verschiedenen Arten und seine Anwendungen vorgestellt. Nach einer Einführung in relevante integrierte Funktionen und Add-ins werden wir anhand von Beispieldaten die Excel-Korrelationsmatrix erstellen, visualisieren und interpretieren.

Was ist eine Korrelationsmatrix?

Die Korrelation ist ein statistisches Maß, das beschreibt, inwieweit zwei oder mehr Variablen miteinander verbunden sind. Sie gibt die Stärke und Richtung einer Beziehung zwischen Variablen an.

Wenn Variablen miteinander korreliert sind, bedeutet das, dass Veränderungen in einer Variable mit Veränderungen in einer anderen verbunden sind - entweder positiv oder negativ:

• Positive Korrelation: Wenn zwei Variablen gemeinsam steigen oder fallen, sind sie positiv korreliert. Zum Beispiel sind Größe und Gewicht in der Regel positiv korreliert; wenn die Größe zunimmt, nimmt auch das Gewicht tendenziell zu.
• Negative Korrelation: Wenn eine Variable steigt, während die andere sinkt. Zum Beispiel die Geschwindigkeit, mit der ein Fahrzeug fährt, und die Zeit, die es braucht, um ein Ziel zu erreichen; je höher die Geschwindigkeit, desto kürzer die Zeit.

Korrelationskoeffizienten sind numerische Maße, die die Stärke und Richtung dieser Beziehung quantifizieren. Der Grad der Korrelation kann mit verschiedenen statistischen Instrumenten gemessen werden, wobei der Pearson-Korrelationskoeffizient am häufigsten verwendet wird.

Den Pearson-Koeffizienten verstehen

Der Pearson-Korrelationskoeffizient, oft auch einfach als "Pearson's r" bezeichnet, ist ein Maß für die lineare Korrelation zwischen zwei Variablen 𝑋 und 𝑌. Er gibt an, inwieweit eine Beziehung zwischen diesen Variablen durch eine gerade Linie beschrieben werden kann.

Der Pearson-Korrelationskoeffizient wird berechnet als die Kovarianz der beiden Variablen geteilt durch das Produkt ihrer Standardabweichungen. Mathematisch lässt sich das so ausdrücken:

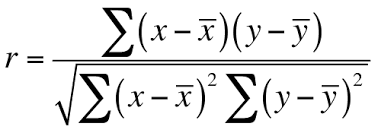
Beachte, dass 𝑋‾und 𝑌‾ die Mittelwerte der Variablen 𝑋 bzw. 𝑌 sind.

Der Wert des berechneten Koeffizienten liegt zwischen -1 und +1, wobei:

• +1 bedeutet eine perfekte positive lineare Beziehung: Wenn eine Variable ansteigt, steigt die andere Variable auf vollkommen lineare Weise.
• -1 bedeutet eine perfekte negative lineare Beziehung: Wenn eine Variable ansteigt, nimmt die andere Variable ganz linear ab.
• 0 bedeutet, dass keine lineare Korrelation besteht: Es gibt keine lineare Beziehung zwischen den Variablen.

Hier siehst du, wie die verschiedenen Arten von Korrelationen aussehen werden:

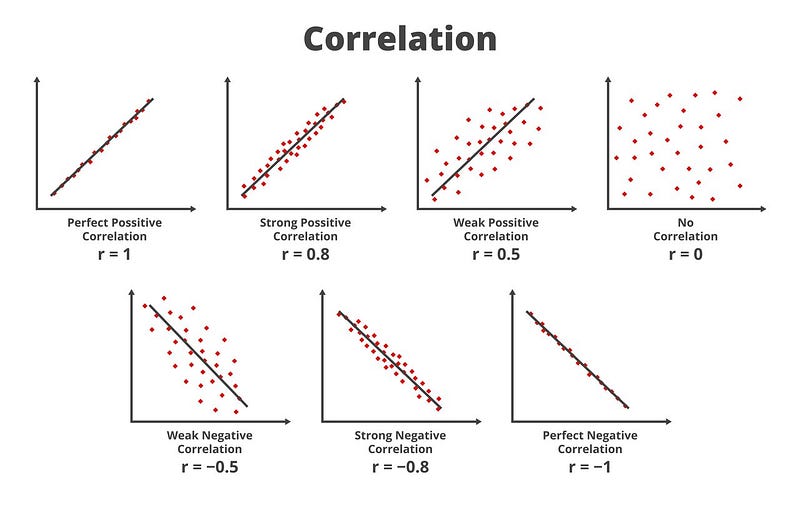Darstellung von Korrelationen(Quelle)

Nachdem wir nun Begriffe wie Korrelation und Korrelationskoeffizienten verstanden haben, wollen wir nun verstehen, wie sich das Ganze zu einer Korrelationsmatrix zusammensetzt.

Eine Korrelationsmatrix ist eine Tabelle, die die Korrelationskoeffizienten zwischen mehreren Variablen anzeigt. Jede Zelle in der Matrix stellt die Korrelation zwischen zwei Variablen dar.

Diese Matrix ist ein nützliches Instrument, um die Stärke und Richtung der Beziehungen zwischen den Variablen in der statistischen Datenanalyse zu analysieren. Neben dieser offensichtlichen Verwendung der Korrelationsmatrix wird sie für verschiedene Anwendungen in der Datenwissenschaft, im Finanzwesen, in der Marktforschung und in anderen Bereichen eingesetzt.

Einige dieser Anwendungen sind:

• In der Datenwissenschaft verwenden wir sie, um Merkmale (Variablen) auf der Grundlage ihrer Beziehungen aus Modellen auszuwählen oder auszuschließen. Stark korrelierte Merkmale können in Regressionsmodellen Multikollinearität verursachen, was die Ergebnisse verfälschen kann. Indem wir diese Korrelationen identifizieren, reduzieren wir Redundanzen und verbessern die Modellleistung.
• In der Finanzwelt werden Korrelationsmatrizen verwendet, um zu verstehen, wie sich verschiedene Vermögenswerte im Verhältnis zueinander bewegen. Dies ist für die Portfoliodiversifizierung und das Risikomanagement von entscheidender Bedeutung, denn es hilft bei der Auswahl von Vermögenswerten, die nicht stark korreliert sind, und reduziert so potenziell das Risiko.
• Unternehmen nutzen Korrelationsmatrizen, um Beziehungen zwischen verschiedenen Verbraucherverhaltensweisen, Produktbewertungen und demografischen Variablen zu finden. Dies hilft, die Ausrichtung und Positionierung von Produkten zu verbessern. Ein ähnliches Beispiel werden wir später in diesem Lernprogramm sehen.

Nachdem wir nun das Konzept der Korrelation, seine Berechnungen und seine Anwendungen verstanden haben, wollen wir uns mit seiner Umsetzung in Excel beschäftigen.

Correlation Matrix: Relevante Funktionen und Add-ins in Excel

Zwei Tools, die wir zur Berechnung von Korrelationsmatrizen in Excel verwenden werden, sind die CORREL-Funktion und das Analysis ToolPak Add-in.

CORREL Funktion

Die CORREL-Funktion in Excel bietet eine einfache Methode, um den Pearson-Korrelationskoeffizienten zwischen zwei Datensätzen zu berechnen.

Die Syntax für die CORREL-Funktion lautet:

CORREL(array1, array2)

wo:

• array1: Dies ist der Bereich der Zellen, der den ersten Datensatz/die erste Spalte enthält.
• array2: Dies ist der Bereich der Zellen, der den zweiten Datensatz/die zweite Spalte enthält.

Jedes Feld muss die gleiche Anzahl von Elementen haben. Excel gibt den Korrelationskoeffizienten für diese Arrays zurück, der von -1 bis +1 reicht.

Analyse-ToolPak

Für umfassendere statistische Analysen, einschließlich der Erstellung einer vollständigen Korrelationsmatrix für mehrere Variablen, kann das Analysis ToolPak in Excel hilfreich sein.

Das Analysis Toolpak muss nicht unbedingt in deinem Excel-Dokument aktiviert sein. Überprüfe, ob das Symbol "Datenanalyse" in der rechten Ecke unter der Registerkarte "Daten" sichtbar ist, wie unten dargestellt.

Analysis Toolpak in Excel.

Wenn du es nicht sehen kannst, mach dir keine Sorgen. Folge den folgenden Schritten und du kannst das Analyse-ToolPak aktivieren.

• Klicke im Menü auf File und wähle dann Options.

Auswahl der Optionen auf der Registerkarte Datei.

• Im Dialogfeld Excel Options wählst du Add-ins.

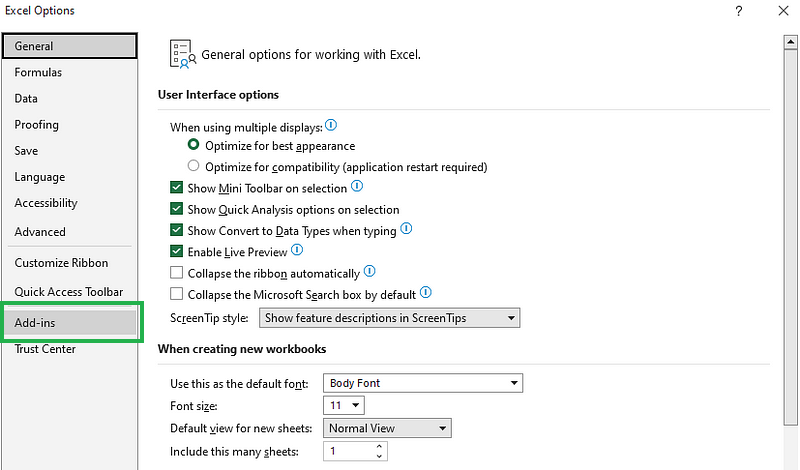
Wählen Sie im Dialogfeld Excel-Optionen die Option Add-Ins.

• Wähle im Feld Manage am unteren Rand der Ansicht Excel Add-ins aus und klicke auf Go.

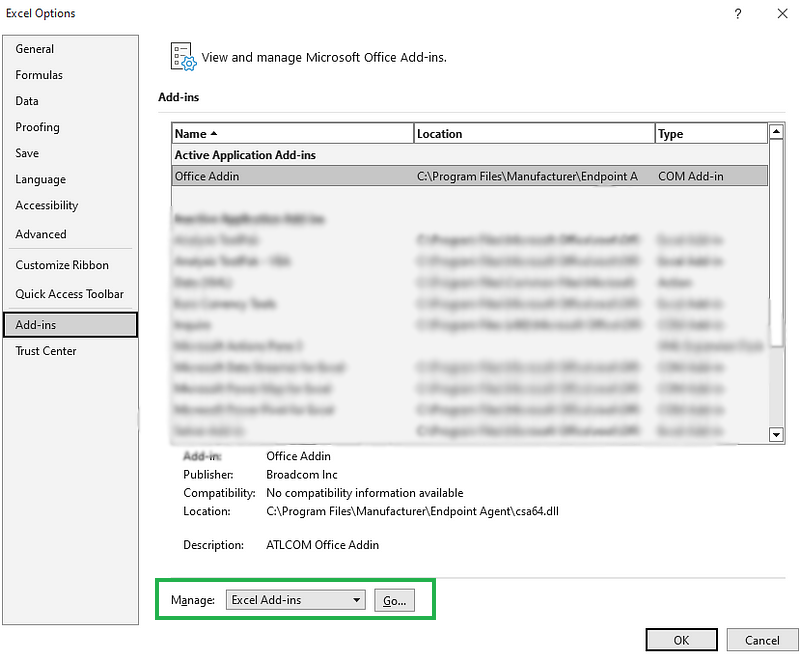
Verwalten von Excel-Add-ins.

• Klicke im Feld Add-Ins auf Analysis ToolPak und dann auf OK.

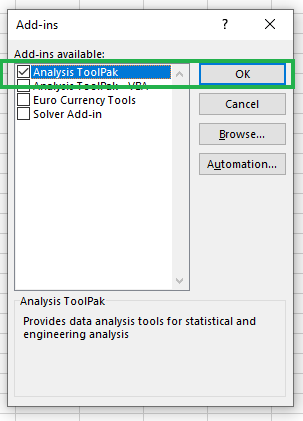
Enabling Analysis Toolpak.

Du solltest das Symbol "Datenanalyse" unter der Registerkarte Data in der Gruppe Analysis sehen können, wenn du die Anweisungen befolgt und es richtig aktiviert hast.

Wie du später sehen wirst, ist die Berechnung der Korrelationsmatrix mit dem Analysis ToolPak viel einfacher und unkomplizierter.

Wie man eine Korrelationsmatrix in Excel erstellt: Ein Beispiel

Stell dir ein Szenario vor, in dem du Datenanalyst bei einem führenden Konsumgüterunternehmen mit mehreren Filialen im ganzen Land bist. Das Unternehmen hat Daten über Verkäufe und demografische Daten der Kunden zusammengestellt.

Dein Ziel ist es, die Zusammenhänge zwischen Kundenmerkmalen und ihrem Kaufverhalten zu verstehen. Ziel dieser Analyse ist es, Produkte zu finden, die häufig zusammen gekauft werden, und zu untersuchen, wie verschiedene demografische Faktoren die Verkaufstrends beeinflussen.

Du hast dich entschieden, eine Korrelationsmatrix für die Analyse zu verwenden. Die folgenden Beispieldaten von 10 Kunden wurden dir in einer Excel-Datei zur Verfügung gestellt:

Beispieldaten von einem führenden Konsumgüterunternehmen.

Die Spalten sind:

• Kunden-ID: Einzigartige Kennung für jeden Kunden.
• Alter: Alter des Kunden in Jahren.
• Jahreseinkommen (K$): Das Jahreseinkommen des Kunden in Tausend Dollar.
• Häufigkeit der Besuche (pro Monat): Wie oft der Kunde den Laden pro Monat besucht.
• Ausgaben pro Besuch ($): Der durchschnittliche Geldbetrag, den der Kunde pro Ladenbesuch ausgibt.
• Elektronik ($) / Kleidung ($) / Lebensmittel ($): Betrag, der pro Besuch für verschiedene Produktkategorien ausgegeben wird.

Korrelationen manuell mit der CORREL-Funktion

Hier sind die Schritte, die du zur Berechnung des Pearson-Korrelationskoeffizienten in Excel befolgen musst:

• Schritt 1: Wähle die entsprechende Zelle aus, die den Teil der Korrelationsmatrix bildet. Hier wählen wir, B16.

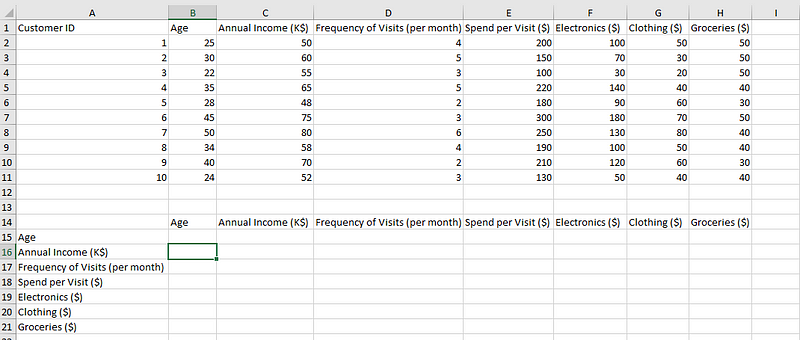
Wähle eine Zelle aus, um die Korrelation zu berechnen.

• Schritt 2: Gib die folgende Formel ein, die die Funktion CORREL verwendet. Wir berechnen zunächst die Korrelation zwischen Alter und Jahreseinkommen.

=CORREL(B2:B11,C2:C11)

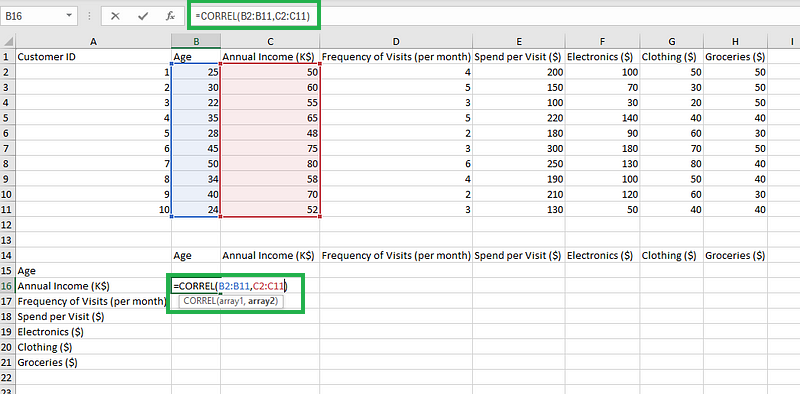
Tippe die Formel ein.

• Schritt 3: Gib die Zelle ein und wiederhole den Vorgang für alle anderen Kombinationen von Spalten.

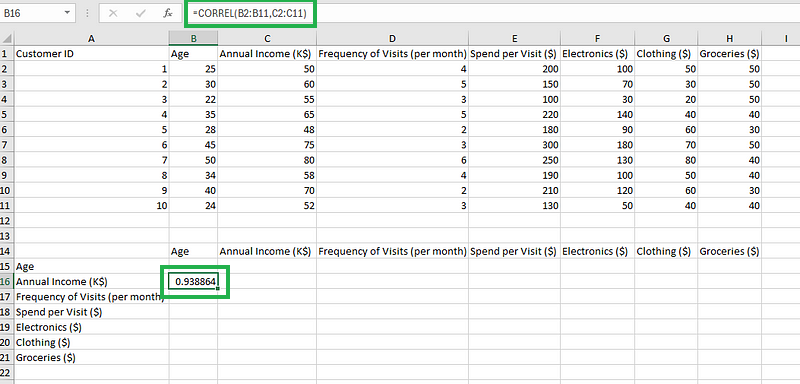
Berechne die Korrelation.

Wie du siehst, kann die manuelle Berechnung der Korrelationswerte für jede Spaltenkombination mühsam werden, besonders wenn die Anzahl der Spalten in den Daten steigt.

Wir haben auch die Möglichkeit, die Funktion OFFSET zu verwenden, um die Änderungen in den Zellbereichen zu automatisieren und die Koeffizientenwerte in die Tabelle einzutragen.

Es ist zwar wichtig zu wissen, dass es die CORREL-Funktion gibt und dass sie nützlich ist, wenn du einzelne Korrelationen berechnest, aber wenn du eine ganze Korrelationsmatrix betrachtest, ist das Analysis Toolpak viel einfacher und schneller und wird daher empfohlen.

Korrelationsmatrix mit Analysis Toolpak

Hier sind die Schritte, die du befolgen solltest, um die Korrelationsmatrix zu erstellen:

• Schritt 1: Klicke auf das Symbol "Datenanalyse" unter der Registerkarte "Daten".

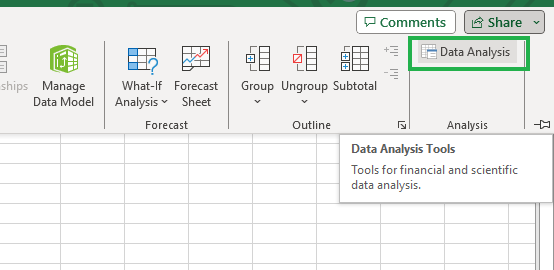
Klicke auf das Symbol Datenanalyse.

• Schritt 2: Wähle die Option "Korrelation" und klicke auf "OK".

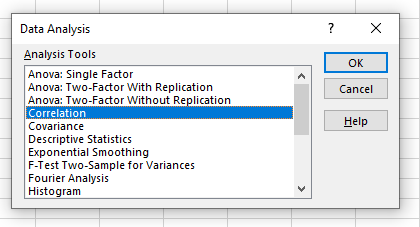
Wähle die Option Korrelation aus.

• Schritt 3: Gib den Eingabebereich an, einschließlich der Spaltennamen. Aktiviere die Option "Etiketten in der ersten Zeile". Als Ausgabebereich wählst du eine beliebige Zelle aus, in der du die Ergebnisse anzeigen möchtest, z.B. $A$14. Zum Schluss drückst du OK.

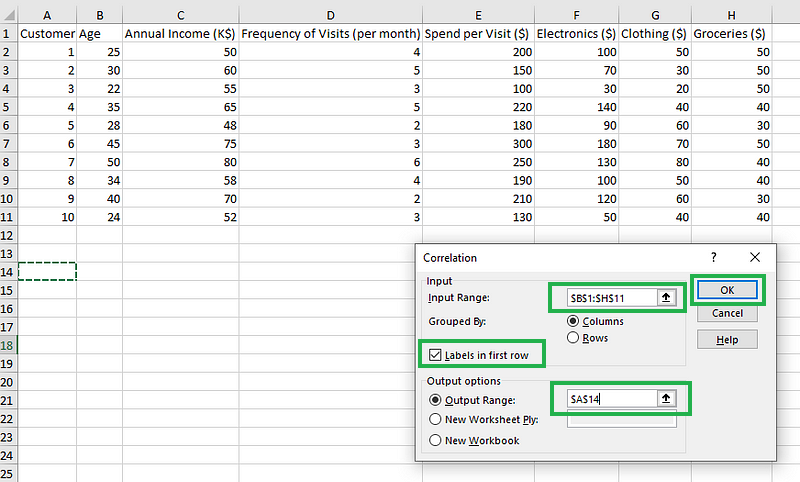
Fülle die Details für Korrelationen mit dem Analysis Toolpak Add-in aus.

Du solltest die Korrelationsmatrix wie unten abgebildet sehen können:

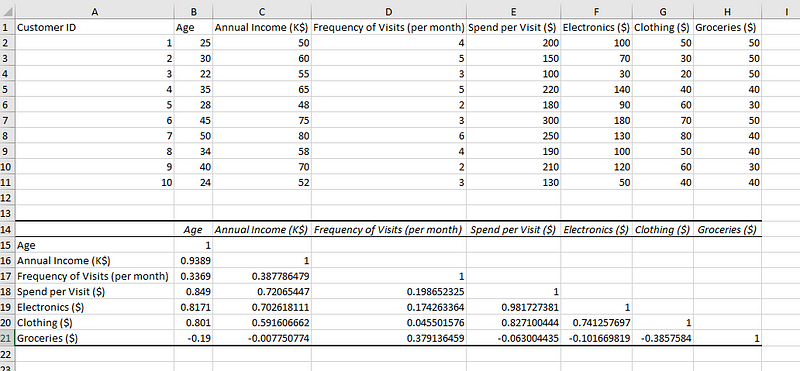
Daten mit ihrer Korrelationsmatrix.

Der Korrelationswert für jede Spalte mit sich selbst ist 1, was eine perfekte Korrelation mit sich selbst bedeutet. Die Matrix hat alle Spalten, die auch in der Zeile vorhanden sind, und bildet alle Kombinationen von Spalten miteinander. Die obere rechte Diagonale der Matrix ist leer, da sie genau den Kombinationen der unteren linken Diagonale entspricht.

Wir haben die Korrelationsmatrix erfolgreich in Excel erstellt. Jetzt ist es an der Zeit zu verstehen, was diese Werte bedeuten und diese Zahlen in Erkenntnisse umzuwandeln.

So interpretierst du eine Korrelationsmatrix in Excel

Die Interpretation der Korrelationsmatrix, die wir oben gesehen haben, ist zwar nicht allzu schwierig, aber sie gerät außer Kontrolle, wenn die Anzahl der Spalten steigt. Es ist unmöglich, jede Kombination durchzugehen, wenn die Anzahl der Spalten hoch ist.

Wir brauchen einen Mechanismus, um die wichtigsten Korrelationen unter allen möglichen Kombinationen in der Korrelationsmatrix schnell zu identifizieren.

Die bedingte Formatierung dieser Zellen in einer Korrelationsmatrix hilft dabei, die Korrelationsmatrix besser zu interpretieren, indem sie unseren Fokus auf die wichtigsten Zellen (dunklere Schattierungen) in der Korrelationsmatrix lenkt.

Hier sind die Schritte zur Farbcodierung der Korrelationsmatrix in Microsoft Excel:

• Schritt 1: Markiere die Korrelationsmatrix (nur die Zahlen) und klicke unter der Registerkarte "Home" auf "Bedingte Formatierung". Klicke auf "Neue Regel" (siehe unten).

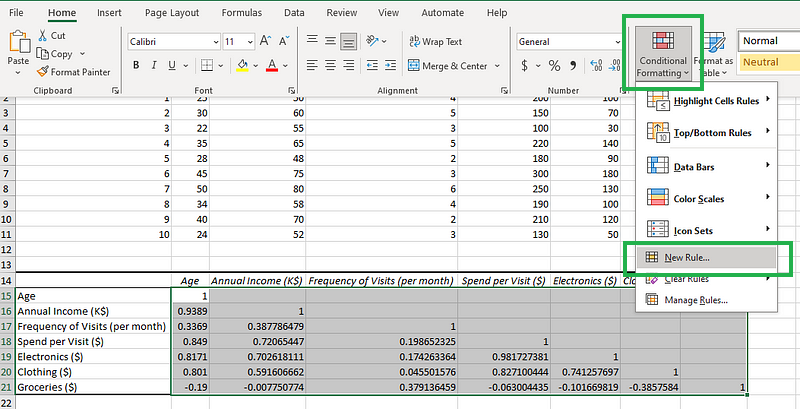
Klicke auf das Symbol "Bedingte Formatierung".

• Schritt 2: Nach Schritt 1 solltest du ein Dialogfeld sehen, wie in der Abbildung unten dargestellt. Wähle zunächst "Alle Zellen auf der Grundlage ihrer Werte formatieren" und stelle die Formatvorlage auf "3-Farben-Skala". Drei Farben sind ideal, weil sie positive, negative und neutrale Korrelationen entsprechend kennzeichnen können. Zum Schluss stellst du den Typ, den Wert und die Farbe ein, wie im Diagramm unten gezeigt.

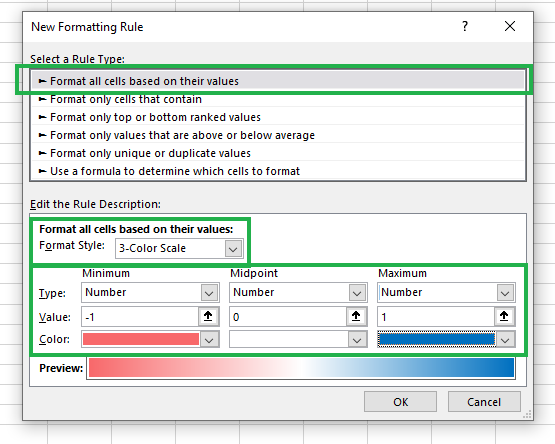
Erstellen einer neuen bedingten Formatierungsregel.

Du erhältst eine Ausgabe wie unten abgebildet:

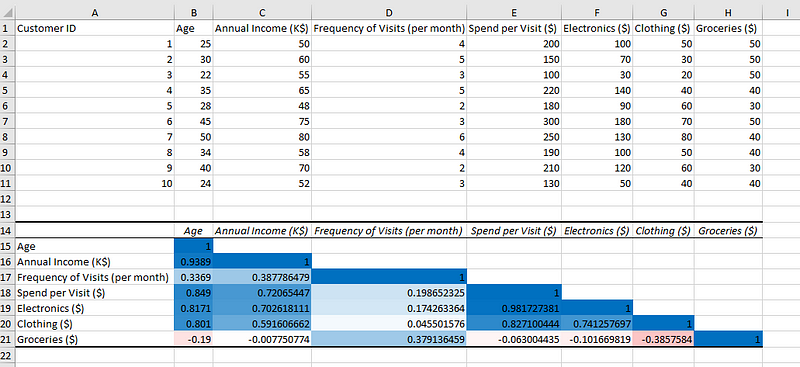
Beispieldaten, mit farbkodierter Korrelationsmatrix.

Das war's! Wir haben Farben hinzugefügt, um die Korrelationsmatrix besser zu visualisieren.

Nachdem wir die Korrelationsmatrix zum besseren Verständnis farblich kodiert haben, können wir aus den erhaltenen Ergebnissen Folgendes ableiten:

• Das Alter ist stark positiv mit dem Jahreseinkommen korreliert, d.h. je älter die Kunden sind, desto stärker ist ihre Kaufkraft.
• Der Betrag, der für Lebensmittel ausgegeben wird, ist mit allen Variablen negativ korreliert, außer mit der Häufigkeit der Kundenbesuche, die positiv korreliert ist, was bedeutet, dass die Kunden wahrscheinlich mehr Lebensmittel kaufen, wenn sie den Laden öfter besuchen.
• Die Kategorien Kleidung und elektronische Geräte weisen eine starke positive Korrelation auf, so dass es eine gute Idee sein kann, diese beiden Kategorien von Artikeln in der Nähe zu haben, um den Umsatz zu steigern.
• Die Kategorien Kleidung und Lebensmittel weisen eine negative Korrelation auf, was bedeutet, dass es am besten ist, diese Kategorien nicht in der Nähe der physischen Läden zu haben.

Der Schlüssel zur Interpretation der Korrelationsmatrix liegt darin, die Richtung und Stärke des Wertes in der Matrix zu beobachten und zu den dazugehörigen Spalten zurückzugehen.

Beachte, dass wir in unseren Erklärungen nie behauptet haben, dass ältere Kunden aufgrund ihres höheren Alters ein höheres Jahreseinkommen haben oder dass ein höherer Verkauf von Kleidung zu einem geringeren Verkauf von Lebensmitteln führt. Denn Korrelation ist nicht gleich Kausalität - ein weit verbreiteter Irrglaube.

Durch eine Korrelationsanalyse können wir nur das Vorhandensein (oder Nichtvorhandensein) einer Beziehung zwischen zwei Variablen interpretieren, aber niemals, dass eine Variable eine Veränderung in der anderen Variable verursacht. Um einen kausalen Zusammenhang festzustellen, müssen wir bestimmte Experimente durchführen. Mehr darüber erfährst du auf in unserem Artikel Korrelation vs. Kausalität. Tutorial zur Verursachung.

Schlussgedanken

In diesem Tutorium wurden das Konzept der Korrelation, der Pearson-Koeffizient, sein mathematischer Ausdruck, verschiedene Arten von Korrelationen und ihre Identifizierung anhand der Richtung und Stärke der Korrelationskoeffizienten vorgestellt.

Dann haben wir uns auf die Umsetzung konzentriert, indem wir Beispieldaten genommen, die Korrelationsmatrix erstellt, mit bedingter Formatierung visualisiert und interpretiert haben. Wir haben uns auch die Missverständnisse bei der Interpretation der Korrelationsmatrix angesehen.

Dein Lernen muss hier nicht enden! Wenn du daran interessiert bist, Korrelationen mit anderen Programmiersprachen zu implementieren, werden dir die folgenden Anleitungen helfen:

• R Korrelation Tutorial
• Python Korrelationstutorial
• SQL-Korrelationskurs

Um dein technisches Wissen zu festigen, schau dir unsere einsteigerfreundlichen Kurse in Probabilistik & Statistik an. Wenn du dich mit den technischen Konzepten sicher fühlst, aber deine praktischen Umsetzungsfähigkeiten in Excel verbessern möchtest, solltest du dir den Lernpfad Excel Fundamentals ansehen.