Implémentation de l'algorithme de Dijkstra en Python : Un tutoriel étape par étape

Pourquoi apprendre l'algorithme de Dijkstra ?

L'algorithme de Dijkstra est l'algorithme de référence pour trouver le chemin le plus court entre deux points d'un réseau, ce qui a de nombreuses applications. Elle est fondamentale en informatique et en théorie des graphes. Comprendre et apprendre à le mettre en œuvre ouvre les portes à des algorithmes et des applications graphiques plus avancés.

Il enseigne également une approche précieuse de la résolution de problèmes grâce à son algorithme gourmand, qui consiste à faire le choix optimal à chaque étape sur la base des informations actuelles.

Cette compétence est transférable à d'autres algorithmes d'optimisation. L'algorithme de Dijkstra n'est peut-être pas le plus efficace dans tous les cas de figure, mais il peut constituer une bonne base de référence pour résoudre les problèmes de la "distance la plus courte".

Voici quelques exemples :

• Systèmes de navigation GPS pour trouver l'itinéraire le plus rapide
• Acheminement des paquets de données dans les réseaux informatiques
• Les services de livraison optimisent leurs itinéraires pour plus d'efficacité
• Réseaux sociaux (suggestion de connexions)
• Finance (recherche de voies d'investissement optimales)
• Gestion de projet (trouver le flux de travail le plus efficace)

Même si vous n'êtes intéressé par aucune de ces choses, l'implémentation de l'algorithme de Dijkstra en Python vous permettra de mettre en pratique des concepts importants tels que :

• Classes Python
• Compréhension des dictionnaires
• Compréhension de listes
• Files d'attente prioritaires

Concepts clés liés aux graphiques

Pour mettre en œuvre l'algorithme de Dijkstra en Python, nous devons rafraîchir quelques concepts essentiels de la théorie des graphes. Tout d'abord, nous avons les graphiques eux-mêmes :

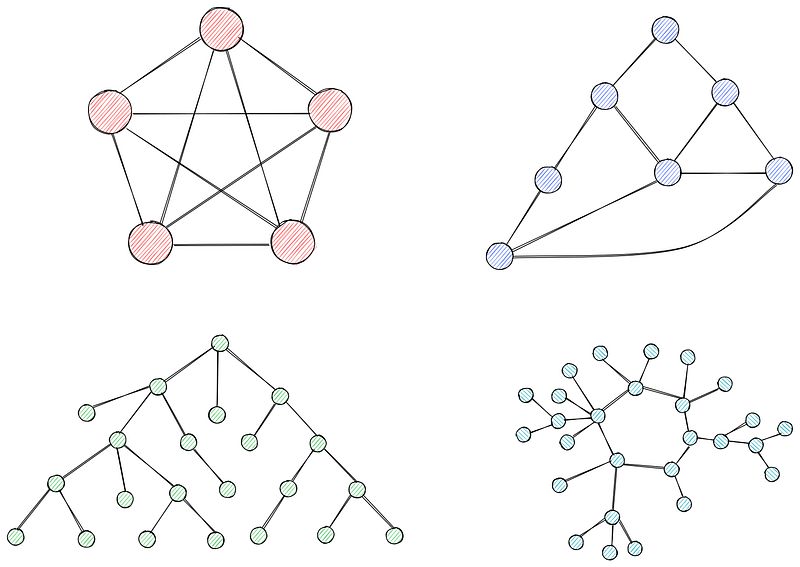
Les graphes sont des collections de nœuds (sommets) reliés par des arêtes. Les nœuds représentent les entités ou les points d'un réseau, tandis que les arêtes représentent la connexion ou les relations entre eux.

Les graphiques peuvent être pondérés ou non pondérés. Dans les graphes non pondérés, toutes les arêtes ont le même poids (souvent fixé à 1). Dans les graphes pondérés (vous l'avez deviné), chaque arête est associée à un poids, qui représente souvent le coût, la distance ou le temps.

Nous utiliserons des graphes pondérés dans ce cours car ils sont nécessaires à l'algorithme de Dijkstra.

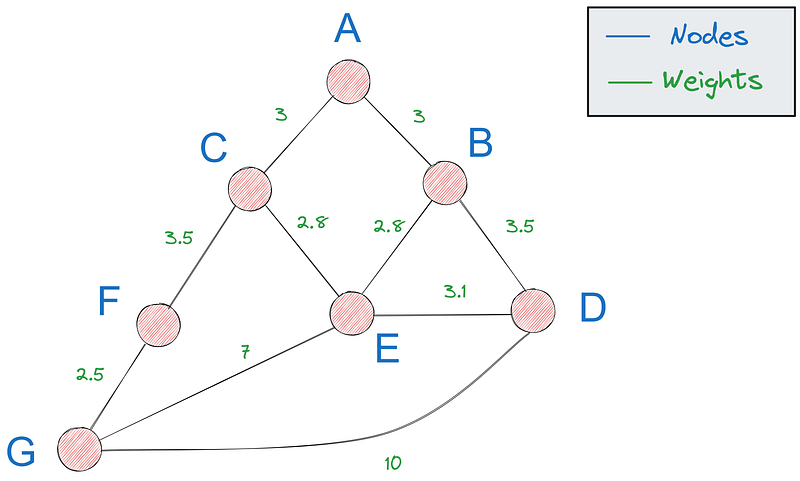
Dans un graphique, un chemin est une séquence de nœuds reliés par des arêtes, commençant et se terminant à des nœuds spécifiques. Le chemin le plus court, qui nous intéresse dans ce tutoriel, est le chemin dont le poids total (distance, coût, etc.) est le plus faible.

L'algorithme de Dijkstra expliqué visuellement

Pour le reste du tutoriel, nous utiliserons le dernier graphique que nous avons vu :

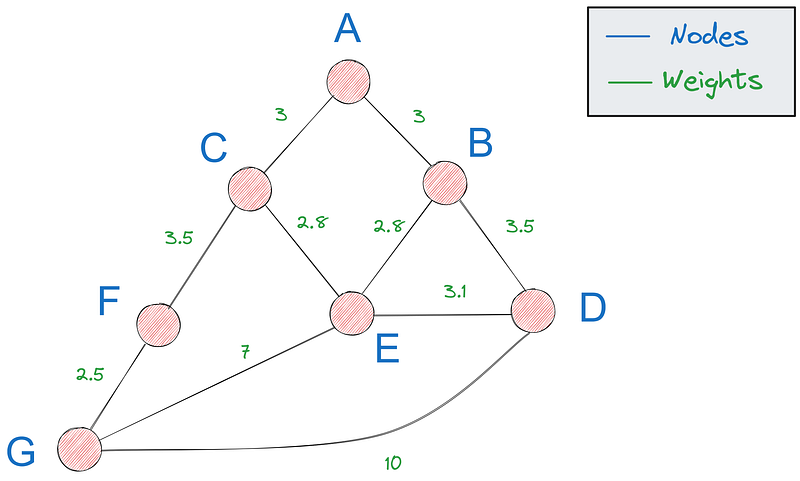
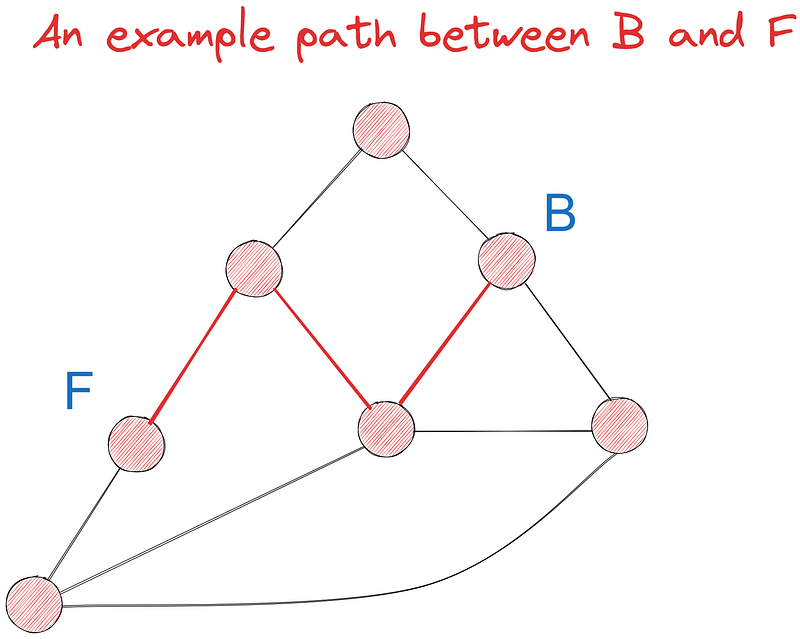
Essayons de trouver le chemin le plus court entre les points B et F à l'aide de l'algorithme de Dijkstra parmi au moins sept chemins possibles. Dans un premier temps, nous effectuerons la tâche visuellement et la mettrons en œuvre dans le code plus tard.

Tout d'abord, nous initialisons l'algorithme comme suit :

1. Nous définissons B comme le nœud racine (source).
2. Nous fixons les distances entre B et tous les autres nœuds à l'infini en tant que valeurs initiales et provisoires de la distance. Nous avons fixé la valeur de B à 0 car il s'agit de la distance à elle-même :

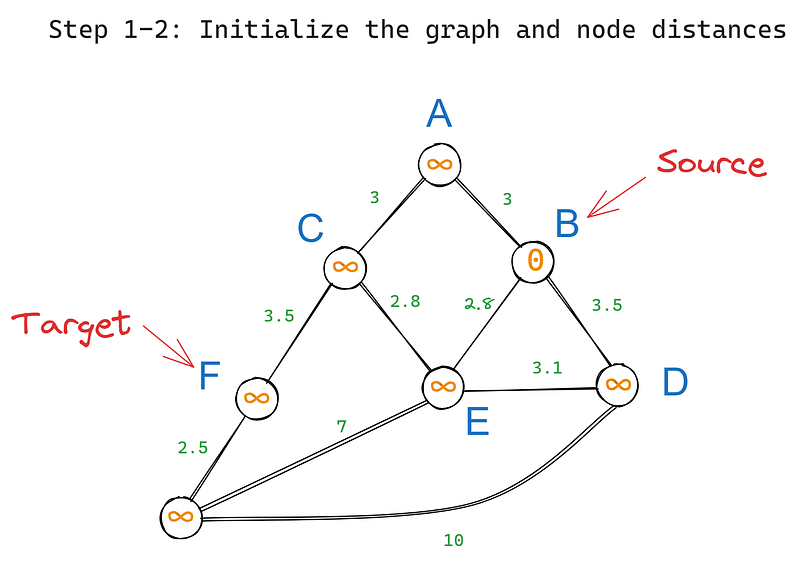
Ensuite, nous exécutons les étapes suivantes de manière itérative :

1. Choisissez le nœud ayant la plus petite valeur comme "nœud actuel" et visitez tous ses nœuds voisins. Lorsque nous visitons chaque voisin, nous mettons à jour leurs valeurs provisoires de l'infini à leurs poids d'arête en commençant par le nœud source.
2. Une fois que tous les voisins du nœud actuel ont été visités, nous marquons le nœud actuel comme "visité". Une fois qu'un nœud est marqué "visité", sa valeur correspond déjà au chemin le plus court à partir de la cible.
3. L'algorithme revient à l'étape 1 et choisit le nœud ayant la plus petite valeur.

Dans notre graphe, B a trois voisins - A, D et E. Visitons chacun d'entre eux en commençant par le nœud racine et mettons à jour leurs valeurs (itération 1) en fonction des poids de leurs arêtes :

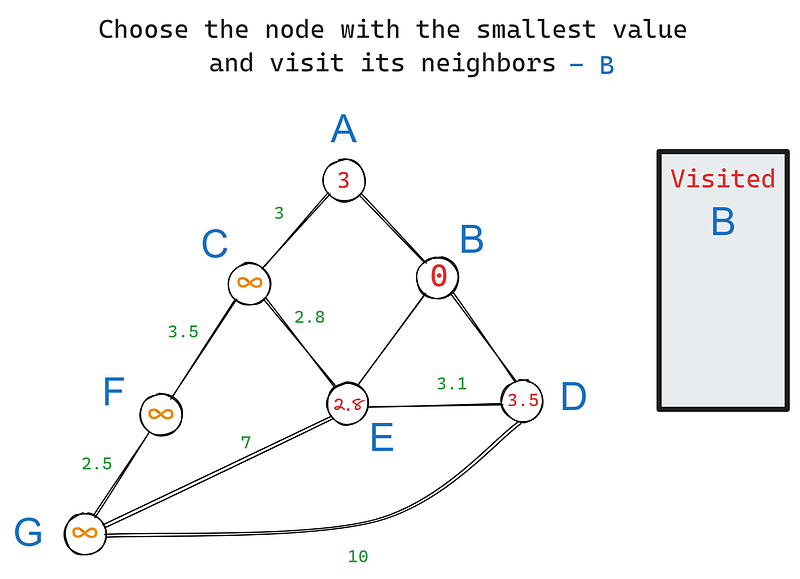
Dans l'itération 2, nous choisissons à nouveau le nœud ayant la plus petite valeur, cette fois - E. Ses voisins sont C, D et G. B est exclu parce que nous l'avons déjà visité. Ses voisins sont C, D et G. B est exclu car nous l'avons déjà visité. Mettons à jour les valeurs des voisins de E :

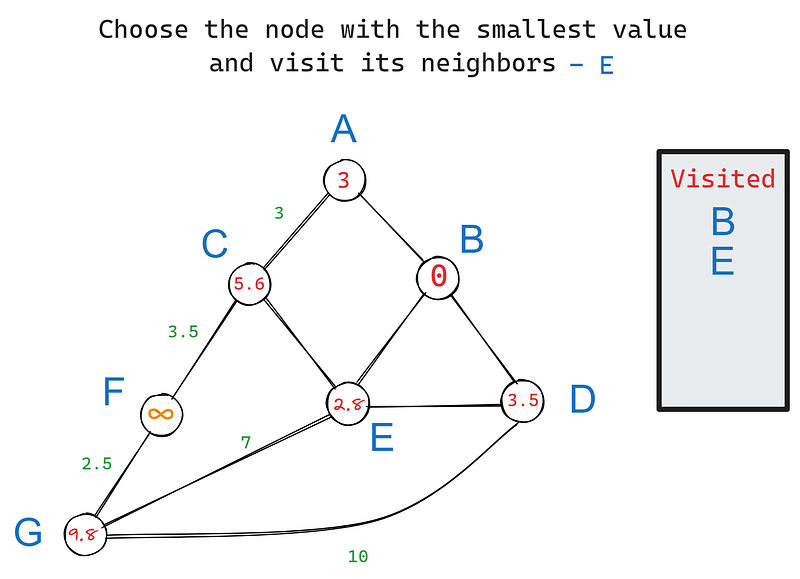
Nous fixons la valeur de C à 5,6 parce que sa valeur est la somme cumulée des poids de B à C. Il en va de même pour G. Cependant, si vous le remarquez, la valeur de D reste à 3,5 alors qu'elle aurait dû être de 3,5 + 2,8 = 6,3, comme pour les autres nœuds.

La règle est la suivante : si la nouvelle somme cumulée est supérieure à la valeur actuelle du nœud, nous ne la mettons pas à jour, car le nœud indique déjà la distance la plus courte vers la racine. Dans ce cas, la valeur actuelle de D (3,5) indique déjà la distance la plus courte vers B car ils sont voisins.

Nous continuons ainsi jusqu'à ce que tous les nœuds aient été visités. Lorsque cela se produira enfin, nous disposerons de la distance la plus courte entre B et chaque nœud et nous pourrons simplement rechercher la valeur de B à F.

En résumé, les étapes sont les suivantes :

1. Initialiser le graphe avec le nœud source qui prend la valeur 0 et tous les autres nœuds à l'infini. Commencez par la source en tant que "nœud actuel".
2. Visitez tous les nœuds voisins du nœud actuel et mettez à jour leurs valeurs en fonction de la somme cumulative des poids (distances) par rapport à la source. Si la valeur actuelle d'un voisin est inférieure à la somme cumulée, elle reste inchangée. Marquez le "nœud actuel" comme terminé.
3. Marquez le nœud de valeur minimale inachevé comme "nœud courant".
4. Répétez les étapes 2 et 3 jusqu'à ce que tous les nœuds soient terminés.

Implémentation pas à pas de l'algorithme de Dijkstra en Python

Maintenant, pour solidifier votre compréhension de l'algorithme de Dijkstra, nous allons apprendre à le mettre en œuvre en Python, étape par étape.

Comprendre les graphes comme des dictionnaires

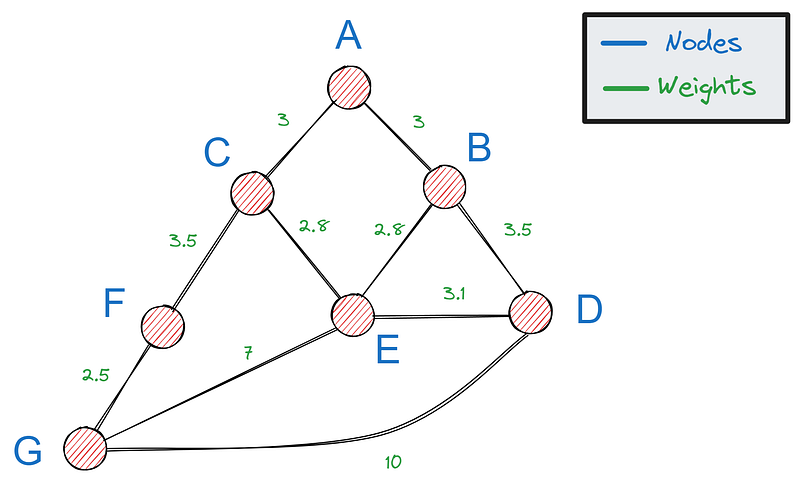
Tout d'abord, nous avons besoin d'un moyen de représenter les graphes en Python - l'option la plus populaire est l'utilisation d'un dictionnaire. S'il s'agit de notre graphique :

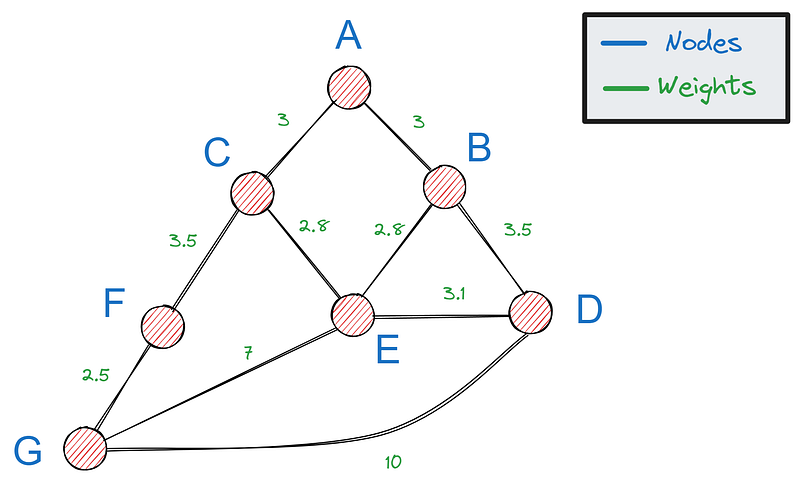
Nous pouvons le représenter par le dictionnaire suivant :

graph = {
   "A": {"B": 3, "C": 3},
   "B": {"A": 3, "D": 3.5, "E": 2.8},
   "C": {"A": 3, "E": 2.8, "F": 3.5},
   "D": {"B": 3.5, "E": 3.1, "G": 10},
   "E": {"B": 2.8, "C": 2.8, "D": 3.1, "G": 7},
   "F": {"G": 2.5, "C": 3.5},
   "G": {"F": 2.5, "E": 7, "D": 10},
}

Chaque clé du dictionnaire est un nœud et chaque valeur est un dictionnaire contenant les voisins de la clé et les distances par rapport à celle-ci. Notre graphe comporte sept nœuds, ce qui signifie que le dictionnaire doit avoir sept clés.

D'autres sources font souvent référence au dictionnaire ci-dessus en tant que liste d'adjacence de dictionnaire. Nous nous en tiendrons désormais à ce terme.

1. Création d'un Graph classe

Pour rendre notre code plus modulaire et plus facile à suivre, nous allons implémenter une simple classe Graph pour représenter les graphes. Sous le capot, il utilisera une liste d'adjacence dictionnaire. Il disposera également d'une méthode permettant d'ajouter facilement des connexions entre deux nœuds :

class Graph:
   def __init__(self, graph: dict = {}):
       self.graph = graph  # A dictionary for the adjacency list

   def add_edge(self, node1, node2, weight):
       if node1 not in self.graph:  # Check if the node is already added
           self.graph[node1] = {}  # If not, create the node
       self.graph[node1][node2] = weight  # Else, add a connection to its neighbor

En utilisant cette classe, nous pouvons construire notre graphe de manière itérative à partir de zéro, comme suit :

G = Graph()

# Add A and its neighbors
G.add_edge("A", "B", 3)
G.add_edge("A", "C", 3)

# Add B and its neighbors
G.add_edge("B", "A", 3)
G.add_edge("B", "D", 3.5)
G.add_edge("B", "E", 2.8)

...

Nous pouvons également transmettre directement une liste d'adjacence de dictionnaire, ce qui est une méthode plus rapide :

# Use the dictionary we defined earlier
G = Graph(graph=graph)

G.graph

{'A': {'B': 3, 'C': 3},
'B': {'A': 3, 'D': 3.5, 'E': 2.8},
'C': {'A': 3, 'E': 2.8, 'F': 3.5},
'D': {'B': 3.5, 'E': 3.1, 'G': 10},
'E': {'B': 2.8, 'C': 2.8, 'D': 3.1, 'G': 7},
'F': {'G': 2.5, 'C': 3.5},
'G': {'F': 2.5, 'E': 7, 'D': 10}}

2. Utilisation d'un dictionnaire pour stocker les distances par rapport à la source

Nous créons une autre méthode de classe - cette fois pour l'algorithme lui-même -shortest_distances:

class Graph:
   def __init__(self, graph: dict = {}):
       self.graph = graph

   # The add_edge method omitted for space

   def shortest_distances(self, source: str):
       # Initialize the values of all nodes with infinity
       distances = {node: float("inf") for node in self.graph}
       distances[source] = 0  # Set the source value to 0

       ...

La première chose que nous faisons dans la méthode est de définir un dictionnaire qui contient des paires nœud-valeur. Ce dictionnaire est mis à jour chaque fois que nous visitons un nœud et ses voisins. Comme nous l'avons mentionné dans l'explication visuelle de l'algorithme, les valeurs initiales de tous les nœuds sont fixées à l'infini, tandis que la valeur de la source est de 0.

Lorsque nous aurons fini d'écrire la méthode, ce dictionnaire sera renvoyé, et il contiendra les distances les plus courtes vers tous les nœuds à partir de la source. Nous pourrons trouver la distance de B à F de cette manière :

# Sneak-peek - find the shortest paths from B
distances = G.shortest_distances("B")

to_F = distances["F"]
print(f"The shortest distance from B to F is {to_F}")

3. Utilisation d'une file d'attente prioritaire pour itérer sur les nœuds

Il nous faut maintenant un moyen de parcourir les nœuds du graphe en suivant les règles de l'algorithme de Dijkstra. Si vous vous en souvenez, à chaque itération, nous devons choisir le nœud ayant la plus petite valeur et visiter ses voisins.

Vous pourriez dire que nous pouvons simplement passer en boucle sur les clés du dictionnaire :

for node in graph.keys():
   ...

Cette méthode ne fonctionne pas car elle ne permet pas de trier les nœuds en fonction de leur valeur. De simples tableaux ne suffiront donc pas. Pour résoudre cette partie du problème, nous utiliserons ce que l'on appelle une file d'attente prioritaire.

Une file d'attente prioritaire est semblable à une liste ordinaire (tableau), mais chacun de ses éléments possède une valeur supplémentaire représentant sa priorité. Il s'agit d'un exemple de file d'attente prioritaire :

pq = [(3, "A"), (1, "C"), (7, "D")]

Cette file d'attente contient trois éléments - A, C et D - et chacun d'eux possède une valeur de priorité qui détermine la manière dont les opérations sont effectuées dans la file d'attente. Python fournit une bibliothèque heapq intégrée pour travailler avec les files d'attente prioritaires :

from heapq import heapify, heappop, heappush

La bibliothèque a trois fonctions qui nous intéressent :

• heapify: Transforme une liste de tuples avec des paires priorité-valeur en une file d'attente prioritaire.
• heappush: Ajoute un élément à la file d'attente avec la priorité qui lui est associée.
• heappop: Supprime et renvoie l'élément ayant la plus haute priorité (l'élément ayant la plus petite valeur).

pq = [(3, "A"), (1, "C"), (7, "D")]

# Convert into a queue object
heapify(pq)

# Return the highest priority value
heappop(pq)

(1, 'C')

Comme vous pouvez le voir, après avoir converti pq en file d'attente à l'aide de heapify, nous avons pu extraire C en fonction de sa priorité. Essayons de pousser une valeur :

heappush(pq, (0, "B"))

heappop(pq)

(0, 'B')

La file d'attente est correctement mise à jour en fonction de la priorité du nouvel élément car heappop a renvoyé le nouvel élément avec une priorité de 0.

Notez qu'une fois qu'un élément est sorti, il ne fait plus partie de la file d'attente.

Pour en revenir à notre algorithme, après avoir initialisé distances, nous créons une nouvelle file d'attente prioritaire qui ne contient initialement que le nœud source :

class Graph:
   def __init__(self, graph: dict = {}):
       self.graph = graph

   def shortest_distances(self, source: str):
       # Initialize the values of all nodes with infinity
       distances = {node: float("inf") for node in self.graph}
       distances[source] = 0  # Set the source value to 0

       # Initialize a priority queue
       pq = [(0, source)]
       heapify(pq)

       # Create a set to hold visited nodes
       visited = set()

La priorité de chaque élément à l'intérieur de pq sera sa valeur actuelle. Nous initialisons également un ensemble vide pour enregistrer les nœuds visités.

4. L'algorithme de Dijkstra en tant que while boucle

Nous commençons maintenant à parcourir tous les nœuds non visités à l'aide d'une boucle while:

class Graph:
   def __init__(self, graph: dict = {}):
       self.graph = graph

   def shortest_distances(self, source: str):
       # Initialize the values of all nodes with infinity
       distances = {node: float("inf") for node in self.graph}
       distances[source] = 0  # Set the source value to 0

       # Initialize a priority queue
       pq = [(0, source)]
       heapify(pq)

       # Create a set to hold visited nodes
       visited = set()

       while pq:  # While the priority queue isn't empty
           current_distance, current_node = heappop(
               pq
           )  # Get the node with the min distance

           if current_node in visited:
               continue  # Skip already visited nodes
           visited.add(current_node)  # Else, add the node to visited set

Tant que la file d'attente des priorités n'est pas vide, nous continuons d'extraire le nœud le plus prioritaire (avec la valeur minimale) et d'extraire sa valeur et son nom vers current_distance et current_node. Si le site current_node se trouve à l'intérieur du site visited, nous l'ignorons. Dans le cas contraire, nous le marquons comme visité, puis nous passons à la visite de ses voisins :

while pq:  # While the priority queue isn't empty
   current_distance, current_node = heappop(pq)

   if current_node in visited:
       continue 
   visited.add(current_node)

   for neighbor, weight in self.graph[current_node].items():
       # Calculate the distance from current_node to the neighbor
       tentative_distance = current_distance + weight
       if tentative_distance < distances[neighbor]:
           distances[neighbor] = tentative_distance
           heappush(pq, (tentative_distance, neighbor))

return distances

Pour chaque voisin, nous calculons la distance provisoire par rapport au nœud actuel en ajoutant la valeur actuelle du voisin au poids de l'arête de connexion. Ensuite, nous vérifions si la distance est inférieure à la distance du voisin dans distances. Si c'est le cas, nous mettons à jour le dictionnaire distances et ajoutons le voisin avec sa distance provisoire à la file d'attente prioritaire.

C'est tout ! Nous avons mis en œuvre l'algorithme de Dijkstra. Testons-le :

G = Graph(graph)

distances = G.shortest_distances("B")
print(distances, "\n")

to_F = distances["F"]
print(f"The shortest distance from B to F is {to_F}")

{'A': 3, 'B': 0, 'C': 5.6, 'D': 3.5, 'E': 2.8, 'F': 9.1, 'G': 9.8}

The shortest distance from B to F is 9.1

La distance de B à F est donc de 9,1. Mais attendez : de quel chemin s'agit-il ?

5. Construire le chemin le plus court

Nous ne disposons donc que des distances les plus courtes et non des chemins, ce qui donne à notre graphique l'allure suivante :

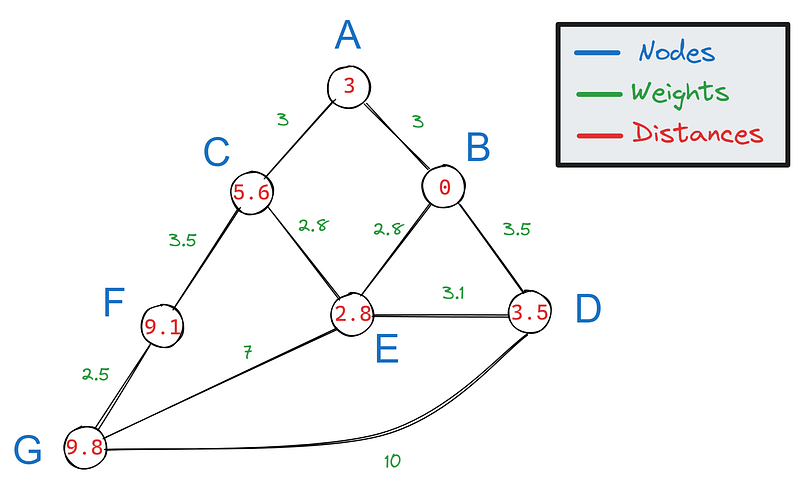
Pour construire le chemin le plus court à partir de la distance la plus courte calculée, nous pouvons revenir sur nos pas à partir de la cible. Pour chaque arête connectée à F, nous soustrayons son poids :

1. 9.1–3.5 = 5.6
2. 9.1–2.5 = 6.5

Ensuite, nous vérifions si l'un des résultats correspond à la valeur des voisins de F. Seul 5,6 correspond à la valeur de C, ce qui signifie que C fait partie du chemin le plus court.

Nous répétons ce processus pour les voisins de C, A et E :

1. 5.6–3 = 2.6
2. 5.6–2.8 = 2.8

Puisque 2,8 correspond à la valeur de E, il fait partie du chemin le plus court. E est également le voisin de B, ce qui fait que le chemin le plus court entre B et F est BECF.

Ajoutons la mise en œuvre de ce processus à notre classe. Le code lui-même est un peu différent de l'explication ci-dessus car il trouve les chemins les plus courts entre B et tous les autres nœuds, et pas seulement F.

Il le fait également en sens inverse, mais l'idée est la même.

Ajoutez les lignes de code suivantes à la fin de la méthode shortest_distances en supprimant l'ancienne déclaration return:

predecessors = {node: None for node in self.graph}

for node, distance in distances.items():
   for neighbor, weight in self.graph[node].items():
       if distances[neighbor] == distance + weight:
           predecessors[neighbor] = node

return distances, predecessors

Lorsque le code est exécuté, le dictionnaire predecessors contient le parent immédiat de chaque nœud impliqué dans le chemin le plus court vers la source. Essayons :

G = Graph(graph)

distances, predecessors = G.shortest_distances("B")

print(predecessors)

{'A': 'B', 'B': None, 'C': 'E', 'D': 'B', 'E': 'B', 'F': 'C', 'G': 'E'}

Commençons par trouver manuellement le chemin le plus court à l'aide du dictionnaire predecessors en remontant à partir de F :

# Check the predecessor of F
predecessors["F"]

'C'  # It is C

# Check the predecessor of C
predecessors["C"]

'E'  # It is E

# Check the predecessor of E
predecessors["E"]

'B'  # It is B

Nous y voilà ! Le dictionnaire indique correctement que le chemin le plus court entre B et F est BECF.

Mais nous avons trouvé la méthode de manière semi-manuelle. Nous voulons une méthode qui renvoie automatiquement le chemin le plus court construit à partir du dictionnaire predecessors, de n'importe quelle source à n'importe quelle cible. Nous définissons cette méthode comme shortest_path (ajoutez-la à la fin de la classe) :

def shortest_path(self, source: str, target: str):
   # Generate the predecessors dict
   _, predecessors = self.shortest_distances(source)

   path = []
   current_node = target

   # Backtrack from the target node using predecessors
   while current_node:
       path.append(current_node)
       current_node = predecessors[current_node]

   # Reverse the path and return it
   path.reverse()

   return path

En utilisant la fonction shortest_distances, nous générons le dictionnaire predecessors. Ensuite, nous lançons une boucle while qui revient en arrière d'un nœud à partir du nœud actuel à chaque itération jusqu'à ce que le nœud source soit atteint. Ensuite, nous renvoyons la liste inversée, qui contient le chemin de la source à la cible.

Testons-le :

G = Graph(graph)

G.shortest_path("B", "F")

['B', 'E', 'C', 'F']

Cela fonctionne ! Essayons-en un autre :

G.shortest_path("A", "G")

['A', 'C', 'F', 'G']

Comme la pluie.

Conclusion

Dans ce tutoriel, nous avons appris l'un des algorithmes les plus fondamentaux de la théorie des graphes, celui de Dijkstra. Il s'agit souvent de l'algorithme de référence pour trouver le chemin le plus court entre deux points dans des structures graphiques. En raison de sa simplicité, il trouve des applications dans de nombreuses industries telles que :

• Logistique et transport
• Réseaux et télécommunications
• Fabrication et robotique
• Finance et investissement
• Urbanisme

J'espère que la mise en œuvre de l'algorithme de Dijkstra en Python a éveillé votre intérêt pour le monde merveilleux des algorithmes de graphes. Si vous souhaitez en savoir plus, je vous recommande vivement les ressources suivantes :

• Cours d'introduction à l'analyse des réseaux en Python
• Cours sur les structures de données et les algorithmes en Python