El aprendizaje automático consiste en predecir y clasificar datos y, para ello, se emplean diversos modelos de aprendizaje automático en función del conjunto de datos. Los modelos de aprendizaje automático se parametrizan para que su comportamiento pueda ajustarse a un problema determinado. Estos modelos pueden tener muchos parámetros y encontrar la mejor combinación de parámetros puede tratarse como un problema de búsqueda. Pero este mismo término llamado parámetro puede parecerte desconocido si eres nuevo en el aprendizaje automático aplicado. Pero no te preocupes. Lo conocerás en el primer lugar de este blog, y también descubrirás cuál es la diferencia entre un parámetro y un hiperparámetro de un modelo de aprendizaje automático. Este blog consta de las siguientes secciones:
- ¿Qué es un parámetro en un modelo de aprendizaje automático?
- ¿Qué es un hiperparámetro en un modelo de aprendizaje automático?
- ¿Por qué es vital optimizar/ajustar los hiperparámetros para mejorar el rendimiento de tu modelo?
- Dos estrategias sencillas para optimizar/ajustar los hiperparámetros
- Un caso práctico sencillo en Python con las dos estrategias
¡Saltemos directamente a la primera sección!
¿Qué es un parámetro en un modelo de aprendizaje automático?
Un parámetro del modelo es una variable de configuración interna al modelo cuyo valor puede estimarse a partir de los datos dados.
- El modelo los necesita para hacer predicciones.
- Sus valores definen la habilidad del modelo en tu problema.
- Se estiman o aprenden a partir de los datos.
- A menudo no son fijados manualmente por el profesional.
- A menudo se guardan como parte del modelo aprendido.
Por lo tanto, lo que debes aprender de los puntos anteriores es que los parámetros son cruciales para los algoritmos de aprendizaje automático. Además, son la parte del modelo que se aprende a partir de los datos históricos de entrenamiento. Profundicemos un poco más. Piensa en los parámetros de las funciones que utilizas al programar en general. Puedes pasar un parámetro a una función. En este caso, un parámetro es un argumento de función que puede tener uno o varios valores. En el aprendizaje automático, el modelo concreto que utilizas es la función y requiere parámetros para hacer una predicción sobre nuevos datos. El hecho de que un modelo tenga un número fijo o variable de parámetros determina si puede denominarse "paramétrico" o "no paramétrico".
Algunos ejemplos de parámetros del modelo son
- Los pesos en una red neuronal artificial.
- Los vectores de soporte en una máquina de vectores de soporte.
- Los coeficientes de una regresión lineal o de una regresión logística.
¿Qué es un hiperparámetro en un modelo de aprendizaje automático?
Un hiperparámetro del modelo es una configuración externa al modelo y cuyo valor no puede estimarse a partir de los datos.
- A menudo se utilizan en los procesos para ayudar a estimar los parámetros del modelo.
- A menudo los especifica el profesional.
- A menudo pueden fijarse utilizando la heurística.
- A menudo se ajustan para un determinado problema de modelado predictivo.
No puedes conocer el mejor valor para un hiperparámetro del modelo en un problema determinado. Puedes utilizar reglas empíricas, copiar valores utilizados en otras ediciones o buscar el mejor valor por ensayo y error. Cuando se ajusta un algoritmo de aprendizaje automático para un problema concreto, en esencia se están ajustando los hiperparámetros del modelo para descubrir los parámetros del modelo que dan lugar a las predicciones más hábiles.
Según un libro muy popular llamado "Applied Predictive Modelling" - "Muchos modelos tienen parámetros importantes que no pueden estimarse directamente a partir de los datos. Por ejemplo, en el modelo de clasificación K-vecino más próximo... Este tipo de parámetro del modelo se denomina parámetro de ajuste porque no se dispone de una fórmula analítica para calcular un valor adecuado."
A menudo se hace referencia a los hiperparámetros del modelo como parámetros del modelo, lo que puede crear confusión. Una buena regla general para superar esta confusión es la siguiente: "Si tienes que especificar manualmente un parámetro del modelo, probablemente se trate de un hiperparámetro del modelo. "Algunos ejemplos de hiperparámetros del modelo son:
- El ritmo de aprendizaje para entrenar una red neuronal.
- Los hiperparámetros C y sigma para las máquinas de vectores soporte.
- La k en vecinos k más próximos.
En la siguiente sección, descubrirás la importancia del conjunto adecuado de valores de hiperparámetros en un modelo de aprendizaje automático.
Cursos populares de aprendizaje automático
Introducción al Aprendizaje Profundo en Python
Importancia del conjunto adecuado de valores de hiperparámetros en un modelo de aprendizaje automático
La mejor forma de pensar en los hiperparámetros es como los ajustes de un algoritmo que pueden ajustarse para optimizar el rendimiento, igual que puedes girar los mandos de una radio AM para obtener una señal clara. Al crear un modelo de aprendizaje automático, se te presentarán opciones de diseño sobre cómo definir la arquitectura de tu modelo. A menudo, no sabes de inmediato cuál debe ser la arquitectura óptima para un modelo determinado, y por eso te gustaría poder explorar un abanico de posibilidades. En un auténtico aprendizaje automático, lo ideal sería que pidieras a la máquina que realizara esta exploración y seleccionara automáticamente la arquitectura óptima del modelo.
En la sección del caso práctico verás cómo la elección correcta de los valores de los hiperparámetros afecta al rendimiento de un modelo de aprendizaje automático. En este contexto, elegir el conjunto adecuado de valores suele denominarse "optimización de hiperparámetros" o "ajuste de hiperparámetros".
Dos estrategias sencillas para optimizar/ajustar los hiperparámetros:
Los modelos pueden tener muchos hiperparámetros y encontrar la mejor combinación de parámetros puede tratarse como un problema de búsqueda.
Aunque actualmente existen muchos algoritmos de optimización/ajuste de hiperparámetros, en este post se analizan dos estrategias sencillas: 1. búsqueda de cuadrícula y 2. búsqueda de cuadrícula. Búsqueda aleatoria.
Búsqueda en cuadrícula de hiperparámetros:
La búsqueda en cuadrícula es un enfoque de la sintonización de hiperparámetros que construirá y evaluará metódicamente un modelo para cada combinación de parámetros del algoritmo especificados en una cuadrícula.
Consideremos el siguiente ejemplo:
Supongamos que un modelo de aprendizaje automático X toma los hiperparámetros a1, a2 y a3. En la búsqueda de cuadrícula, primero defines el intervalo de valores para cada uno de los hiperparámetros a1, a2 y a3. Puedes considerarlo como una matriz de valores para cada uno de los hiperparámetros. Ahora la técnica de búsqueda en cuadrícula construirá muchas versiones de X con todas las combinaciones posibles de los valores de los hiperparámetros (a1, a2 y a3) que definiste en primer lugar. Este intervalo de valores de los hiperparámetros se denomina cuadrícula.
Supongamos que has definido la cuadrícula como:
a1 = [0,1,2,3,4,5]
a2 = [10,20,30,40,5,60]
a3 = [105,105,110,115,120,125]
Ten en cuenta que la matriz de valores que definas para los hiperparámetros debe ser legítima, en el sentido de que no puedes introducir valores de tipo flotante en la matriz si el hiperparámetro sólo admite valores enteros.
Ahora, la búsqueda de cuadrícula comenzará su proceso de construcción de varias versiones de X con la cuadrícula que acabas de definir.
Empezará con la combinación [0,10,105], y terminará con [5,60,125]. Recorrerá todas las combinaciones intermedias entre estas dos, lo que hace que la búsqueda en cuadrícula sea muy costosa computacionalmente.
Veamos la otra técnica de búsqueda Búsqueda aleatoria:
Búsqueda aleatoria de hiperparámetros:
La idea de la búsqueda aleatoria de hiperparámetros fue propuesta por James Bergstra y Yoshua Bengio. Puedes consultar el documento original aquí.
La búsqueda aleatoria difiere de la búsqueda en cuadrícula. En que ya no proporcionas un conjunto discreto de valores a explorar para cada hiperparámetro, sino que proporcionas una distribución estadística para cada hiperparámetro de la que se pueden muestrear valores aleatoriamente.
Antes de seguir adelante, entendamos qué significan distribución y muestreo:
En Estadística, por distribución se entiende esencialmente una disposición de los valores de una variable que muestra su frecuencia de aparición observada o teórica.
Por otra parte, el muestreo es un término utilizado en estadística. Es el proceso de elegir una muestra representativa de una población objetivo y recoger datos de esa muestra para comprender algo sobre la población en su conjunto.
Ahora volvamos de nuevo al concepto de búsqueda aleatoria.
Definirás una distribución de muestreo para cada hiperparámetro. También puedes definir cuántas iteraciones quieres realizar cuando busques el modelo óptimo. En cada iteración, los valores de los hiperparámetros del modelo se establecerán muestreando las distribuciones definidas. Uno de los principales respaldos teóricos para motivar el uso de una búsqueda aleatoria en lugar de una búsqueda cuadriculada es el hecho de que, en la mayoría de los casos, los hiperparámetros no son igual de importantes. Según el documento original:
"....para la mayoría de los conjuntos de datos sólo importan realmente unos pocos de los hiperparámetros, pero que distintos hiperparámetros son importantes en distintos conjuntos de datos. Este fenómeno hace que la búsqueda en cuadrícula sea una mala elección para configurar algoritmos para nuevos conjuntos de datos."
En la siguiente figura, estamos buscando sobre un espacio de hiperparámetros en el que uno de ellos tiene una influencia significativamente mayor en la optimización de la puntuación del modelo: las distribuciones que se muestran en cada eje representan la puntuación del modelo. En cada caso, evaluamos nueve modelos diferentes. La estrategia de búsqueda en cuadrícula pasa por alto descaradamente el modelo óptimo y gasta tiempo redundante explorando el parámetro sin importancia. Durante esta búsqueda en cuadrícula, aislamos cada hiperparámetro y buscamos el mejor valor posible, manteniendo constantes todos los demás hiperparámetros. En los casos en que el hiperparámetro estudiado tiene poco efecto en la puntuación del modelo resultante, esto supone un esfuerzo inútil. Por el contrario, la búsqueda aleatoria tiene un poder exploratorio mucho mayor y puede centrarse en encontrar el valor óptimo del hiperparámetro crítico.
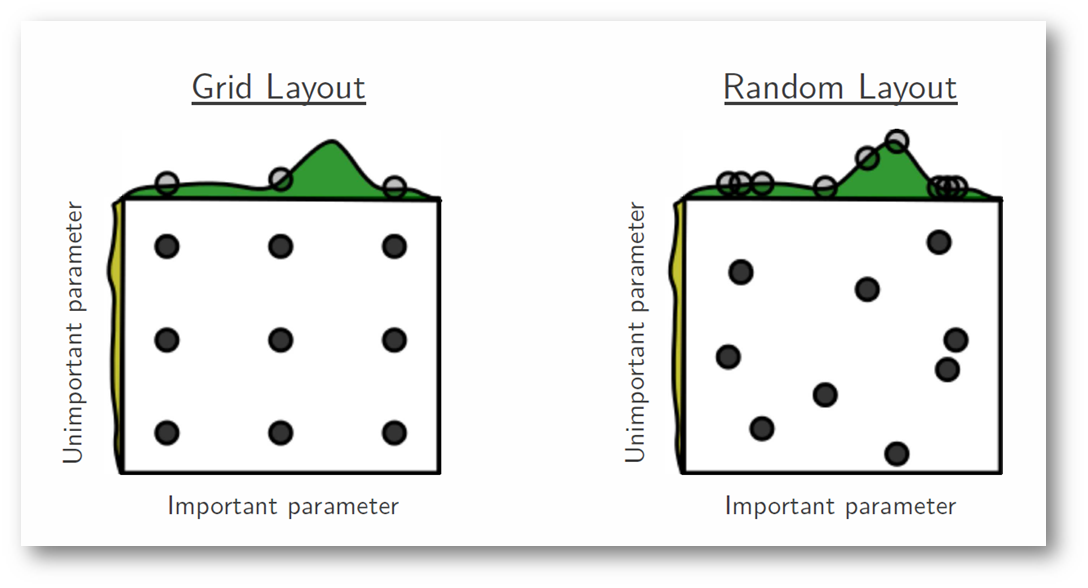
En las secciones siguientes, verás la búsqueda en cuadrícula y la búsqueda aleatoria en acción con Python. También podrás decidir cuál es mejor en cuanto a eficacia y eficiencia.
Caso práctico en Python
El ajuste de hiperparámetros es un paso final en el proceso de aprendizaje automático aplicado antes de presentar los resultados.
Utilizarás el conjunto de datos de diabetes de los indios Pima. El conjunto de datos corresponde a un problema de clasificación en el que tienes que hacer predicciones sobre si una persona va a padecer diabetes dadas las 8 características del conjunto de datos. Puedes encontrar la descripción completa del conjunto de datos aquí.
Hay un total de 768 observaciones en el conjunto de datos. Tu primera tarea es cargar el conjunto de datos para poder continuar. Pero antes vamos a importar las dependencias que vas a necesitar.
# Dependencies
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
Ahora que las dependencias están importadas, vamos a cargar el conjunto de datos de los indios Pima en un objeto Dataframe con la famosa biblioteca Pandas.
data = pd.read_csv("diabetes.csv") # Make sure the .csv file and the notebook are residing on the same directory otherwise supply an absolute path of the .csv file
El conjunto de datos se carga correctamente en los datos del objeto Dataframe. Ahora, echemos un vistazo a los datos.
data.head()

Así que puedes 8 características diferentes etiquetadas en los resultados de 1 y 0, donde 1 significa que la observación tiene diabetes, y 0 denota que la observación no tiene diabetes. Se sabe que el conjunto de datos tiene valores perdidos. Concretamente, faltan observaciones para algunas columnas que están marcadas como valor cero. Podemos corroborarlo por la definición de esas columnas, y el conocimiento del dominio de que un valor cero no es válido para esas medidas, por ejemplo, cero para el índice de masa corporal o la tensión arterial no es válido.
(Los valores perdidos crean muchos problemas cuando intentas construir un modelo de aprendizaje automático. En este caso, utilizarás un clasificador de Regresión Logística para predecir los pacientes que tienen diabetes o no. Ahora bien, la Regresión Logística no puede tratar los problemas de los valores perdidos. )
(Si quieres un repaso rápido sobre la Regresión Logística, puedes consultar aquí).
Vamos a obtener algunas estadísticas sobre los datos con la utilidad describe() de Pandas.
data.describe()

Esto es útil.
Podemos ver que hay columnas que tienen un valor mínimo de cero (0). En algunas columnas, un valor de cero no tiene sentido e indica un valor no válido o que falta.
En concreto, las siguientes columnas tienen un valor mínimo cero no válido:
- Concentración plasmática de glucosa
- Tensión arterial diastólica
- Espesor del pliegue cutáneo del tríceps
- Insulina sérica en 2 horas
- Índice de masa corporal
Ahora tienes que identificar y marcar los valores como ausentes. Confirmémoslo mirando los datos sin procesar, el ejemplo imprime las 20 primeras filas de datos.
data.head(20)

Puedes ver el 0 en varias columnas, ¿verdad?
Puedes obtener un recuento del número de valores perdidos en cada una de estas columnas. Puedes hacerlo marcando como Verdadero todos los valores del subconjunto del Marco de datos que te interese que tengan valores cero. A continuación, puedes contar el número de valores verdaderos de cada columna. Para ello, tendrás que volver a importar los datos sin los nombres de las columnas.
data = pd.read_csv("https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv",header=None)
print((data[[1,2,3,4,5]] == 0).sum())
1 5
2 35
3 227
4 374
5 11
dtype: int64
Puedes ver que las columnas 1,2 y 5 sólo tienen unos pocos valores cero, mientras que las columnas 3 y 4 muestran muchos más, casi la mitad de las filas. Aunque en la columna 0 faltan varios valores, eso es natural. La columna 8 denota la variable objetivo, por lo que los "0" en ella son naturales.
Esto pone de manifiesto que pueden ser necesarias distintas estrategias de "valores perdidos" para distintas columnas, por ejemplo, para garantizar que aún queda un número suficiente de registros para entrenar un modelo predictivo.
En Python, concretamente en Pandas, NumPy y Scikit-Learn, los valores perdidos se marcan como NaN.
Los valores con un valor NaN se ignoran en operaciones como suma, recuento, etc.
Puedes marcar valores como NaN fácilmente con el Pandas DataFrame utilizando la función replace() en un subconjunto de las columnas que te interesen.
Después de marcar los valores perdidos, puedes utilizar la función isnull() para marcar todos los valores NaN del conjunto de datos como Verdaderos y obtener un recuento de los valores perdidos de cada columna.
# Mark zero values as missing or NaN
data[[1,2,3,4,5]] = data[[1,2,3,4,5]].replace(0, np.NaN)
# Count the number of NaN values in each column
print(data.isnull().sum())
0 0
1 5
2 35
3 227
4 374
5 11
6 0
7 0
8 0
dtype: int64
Puedes ver que las columnas 1:5 tienen el mismo número de valores perdidos que los valores cero identificados anteriormente. Esto es señal de que has marcado correctamente los valores perdidos identificados.
Este es un resumen útil. Pero os gustaría ver los datos reales para confirmar que no os habéis engañado.
A continuación se muestra el mismo ejemplo, excepto que imprimes las 5 primeras filas de datos.
data.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148.0 | 72.0 | 35.0 | NaN | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85.0 | 66.0 | 29.0 | NaN | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183.0 | 64.0 | NaN | NaN | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89.0 | 66.0 | 23.0 | 94.0 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137.0 | 40.0 | 35.0 | 168.0 | 43.1 | 2.288 | 33 | 1 |
De los datos brutos se desprende claramente que marcar los valores perdidos tuvo el efecto deseado. Ahora, imputarás los valores que faltan. Imputar se refiere a utilizar un modelo para sustituir los valores que faltan. Aunque existen varias soluciones para imputar los valores perdidos, utilizarás la imputación de la media, que consiste en sustituir los valores perdidos de una columna por la media de esa columna concreta. Hagámoslo con la utilidad fillna() de Pandas.
# Fill missing values with mean column values
data.fillna(data.mean(), inplace=True)
# Count the number of NaN values in each column
print(data.isnull().sum())
0 0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
dtype: int64
Salud. Ya has resuelto el problema del valor perdido. Ahora vamos a utilizar estos datos para construir un modelo de Regresión Logística utilizando scikit-learn.
En primer lugar, verás el modelo con algunos valores aleatorios de los hiperparámetros. A continuación, construirás otros dos modelos de Regresión Logística con dos estrategias diferentes: Búsqueda en cuadrícula y Búsqueda aleatoria.
# Split dataset into inputs and outputs
values = data.values
X = values[:,0:8]
y = values[:,8]
# Initiate the LR model with random hyperparameters
lr = LogisticRegression(penalty='l1',dual=False,max_iter=110)
Has creado el modelo de Regresión Logística con algunos valores aleatorios de hiperparámetros. Los hiperparámetros que has utilizado son:
- pena : Sirve para especificar la norma utilizada en la penalización (regularización).
- dual : Formulación dual o primal. La formulación dual sólo se aplica para la penalización l2 con el solucionador liblineal. Prefiere dual=False cuando n_muestras > n_características.
- max_iter : Número máximo de iteraciones necesarias para converger.
Más adelante, en el caso práctico, optimizarás/ajustarás estos hiperparámetros para ver el cambio en los resultados.
# Pass data to the LR model
lr.fit(X,y)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=110, multi_class='ovr', n_jobs=1,
penalty='l1', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
Es hora de comprobar la puntuación de precisión.
lr.score(X,y)
0.7747395833333334
En el paso anterior, aplicaste tu modelo LR a los mismos datos y evaluaste su puntuación. Pero siempre es necesario validar la estabilidad de tu modelo de aprendizaje automático. No puedes ajustar el modelo a tus datos de entrenamiento y esperar que funcione con precisión para los datos reales que nunca ha visto antes. Necesitas algún tipo de garantía de que tu modelo ha obtenido correctamente la mayoría de los patrones de los datos.
Pues bien, la validación cruzada está ahí para rescatarte. No entraré en detalles al respecto, ya que está fuera del alcance de este blog. Pero este post hace un trabajo muy fino.
# You will need the following dependencies for applying Cross-validation and evaluating the cross-validated score
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
# Build the k-fold cross-validator
kfold = KFold(n_splits=3, random_state=7)
Has indicado n_splits como 3, lo que básicamente lo convierte en una validación cruzada triple. También has indicado el estado_aleatorio como 7. Esto es sólo para reproducir los resultados. También podrías haber proporcionado cualquier valor entero. Ahora, apliquemos esto.
result = cross_val_score(lr, X, y, cv=kfold, scoring='accuracy')
print(result.mean())
0.765625
Puedes ver que hay una ligera disminución en la puntuación. De todos modos, puedes hacerlo mejor con el ajuste / optimización de hiperparámetros.
Vamos a construir otro modelo LR, pero esta vez se afinará su hiperparámetro. Primero harás esta búsqueda en la cuadrícula.
Primero vamos a importar las dependencias que necesitarás. Scikit-learn proporciona una utilidad llamada GridSearchCV para ello.
from sklearn.model_selection import GridSearchCV
Vamos a definir los valores de cuadrícula de los hiperparámetros que has utilizado anteriormente.
dual=[True,False]
max_iter=[100,110,120,130,140]
param_grid = dict(dual=dual,max_iter=max_iter)
Has definido la cuadrícula. Vamos a ejecutar la búsqueda de cuadrícula sobre ellos y ver los resultados con el tiempo de ejecución.
import time
lr = LogisticRegression(penalty='l2')
grid = GridSearchCV(estimator=lr, param_grid=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
grid_result = grid.fit(X, y)
# Summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
Best: 0.752604 using {'dual': False, 'max_iter': 100}
Execution time: 0.3954019546508789 ms
También puedes definir una rejilla mayor de hiperparámetros y aplicar la búsqueda en rejilla.
dual=[True,False]
max_iter=[100,110,120,130,140]
C = [1.0,1.5,2.0,2.5]
param_grid = dict(dual=dual,max_iter=max_iter,C=C)
lr = LogisticRegression(penalty='l2')
grid = GridSearchCV(estimator=lr, param_grid=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
grid_result = grid.fit(X, y)
# Summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
Best: 0.763021 using {'C': 2.0, 'dual': False, 'max_iter': 100}
Execution time: 0.793781042098999 ms
Puedes ver un aumento en la puntuación de precisión, pero también hay un crecimiento suficiente en el tiempo de ejecución. Cuanto mayor sea la cuadrícula, mayor será el tiempo de ejecución.
Volvamos a ejecutarlo todo, pero esta vez con la búsqueda aleatoria. Scikit-learn proporciona RandomSearchCV para hacerlo. Como de costumbre, tendrás que importar las dependencias necesarias para ello.
from sklearn.model_selection import RandomizedSearchCV
random = RandomizedSearchCV(estimator=lr, param_distributions=param_grid, cv = 3, n_jobs=-1)
start_time = time.time()
random_result = random.fit(X, y)
# Summarize results
print("Best: %f using %s" % (random_result.best_score_, random_result.best_params_))
print("Execution time: " + str((time.time() - start_time)) + ' ms')
Best: 0.763021 using {'max_iter': 100, 'dual': False, 'C': 2.0}
Execution time: 0.28888916969299316 ms
¡Woah! La búsqueda aleatoria dio la misma precisión, pero en mucho menos tiempo.
Esto es todo por lo que respecta a la parte del caso práctico. Ahora, ¡vamos a terminar!
Conclusión y lecturas complementarias
En este tutorial, has aprendido sobre los parámetros y los hiperparámetros de un modelo de aprendizaje automático y también sobre sus diferencias. También conocerás el papel que desempeña la optimización de hiperparámetros en la construcción de modelos eficientes de aprendizaje automático. Has construido un sencillo clasificador de Regresión Logística en Python con la ayuda de scikit-learn.
Has ajustado los hiperparámetros con la búsqueda en cuadrícula y la búsqueda aleatoria y has visto cuál funciona mejor.
Además, viste pequeños pasos de preprocesamiento de datos (como el tratamiento de los valores perdidos) que son necesarios antes de introducir tus datos en el modelo de aprendizaje automático. También has cubierto la validación cruzada.
Son muchas cosas que asimilar, y todas ellas son igual de importantes en tu viaje por la ciencia de datos. Te dejo con algunas lecturas adicionales que puedes hacer.
Otras lecturas:
- Problemas en la optimización de hiperparámetros
- Optimización de hiperparámetros con técnicas de soft computing
- Búsqueda aleatoria para la optimización de hiperparámetros
A los que estén un poco más avanzados, les recomiendo encarecidamente que lean este artículo para optimizar eficazmente los hiperparámetros de las redes neuronales. enlace
Si quieres aprender más sobre Aprendizaje Automático, sigue los siguientes cursos de DataCamp: