Teorema de Pitágoras: Explorando la relación fundamental de la geometría

El teorema de Pitágoras es algo más que un elemento básico de la geometría del bachillerato; es una piedra angular del álgebra lineal, que constituye la base para comprender las normas vectoriales, la ortogonalidad y las proyecciones en espacios de dimensiones superiores. Estos conceptos no sólo son fundamentales para la teoría, sino que también tienen aplicaciones prácticas en la ciencia de datos, donde sustentan los algoritmos del aprendizaje automático y la reducción de la dimensionalidad.

En este artículo, empezaré por el principio y repasaré los fundamentos del teorema de Pitágoras, y poco a poco iré avanzando hacia las aplicaciones más avanzadas y menos conocidas del teorema en dimensiones superiores, incluido su papel en el análisis de conjuntos de datos complejos, la optimización de modelos de aprendizaje automático y la visualización de relaciones geométricas en los flujos de trabajo de la ciencia de datos. Si quieres explorar más a fondo estas conexiones y ver cómo se aplican en la práctica, nuestro curso de Álgebra Lineal para la Ciencia de Datos en R ofrece un enfoque práctico para tender un puente entre la teoría y los problemas de datos del mundo real.

Introducción al Teorema de Pitágoras

Imagínate el antiguo Egipto, donde los arquitectos y constructores se enfrentaban a un reto irresistible: crear ángulos rectos perfectos para sus magníficas estructuras. ¿Su ingeniosa solución? Una cuerda simple marcada con 12 secciones iguales. Formando un triángulo con lados de 3, 4 y 5 unidades, descubrieron que podían crear ángulos rectos perfectos siempre.

El teorema de Pitágoras es una de las relaciones más elegantes y prácticas de las matemáticas. Aunque tradicionalmente se atribuye al antiguo matemático griego Pitágoras (570-495 a.C.), las pruebas sugieren que este principio fundamental era conocido por varias civilizaciones antiguas, como la babilónica y la china, más de un milenio antes de que Pitágoras lo demostrara sistemáticamente.

Fórmula del Teorema de Pitágoras

El teorema de Pitágoras expresa una relación clara: en cualquier triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (c) es igual a la suma de los cuadrados de los otros dos lados (a y b). Esta relación aparece en la famosa ecuación

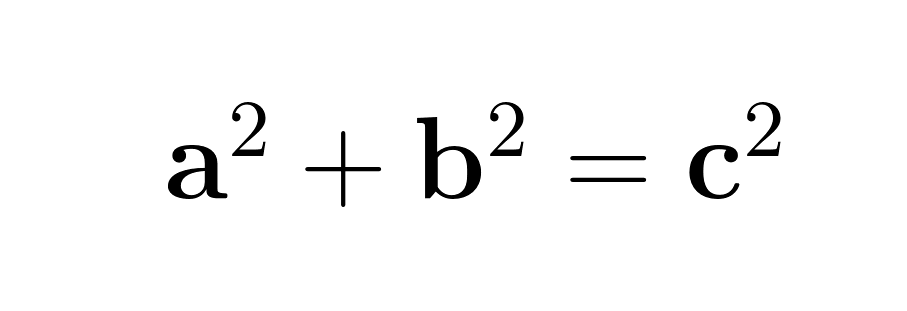
Dónde:

• a y b son las longitudes de los dos catetos (los lados adyacentes al ángulo recto)
• c es la longitud de la hipotenusa (el lado más largo, opuesto al ángulo recto)

Pruebas del Teorema de Pitágoras

Comprender las diferentes demostraciones del teorema de Pitágoras ayuda a revelar por qué esta relación es válida en todas las matemáticas. Exploremos algunos enfoques distintos para demostrar este teorema.

Demostraciones geométricas del teorema de Pitágoras

A lo largo de la historia, los matemáticos han desarrollado numerosas pruebas geométricas del teorema de Pitágoras, cada una de las cuales ofrece una visión única de esta relación fundamental. Exploremos uno de los enfoques visualmente más llamativos, sin dejar de reconocer la rica variedad de demostraciones geométricas disponibles.

La prueba de construcción cuadrada

Una demostración geométrica clásica, popularizada en los Elementosde Euclides , sigue siendo una de las demostraciones visualmente más convincentes del teorema. Funciona así:

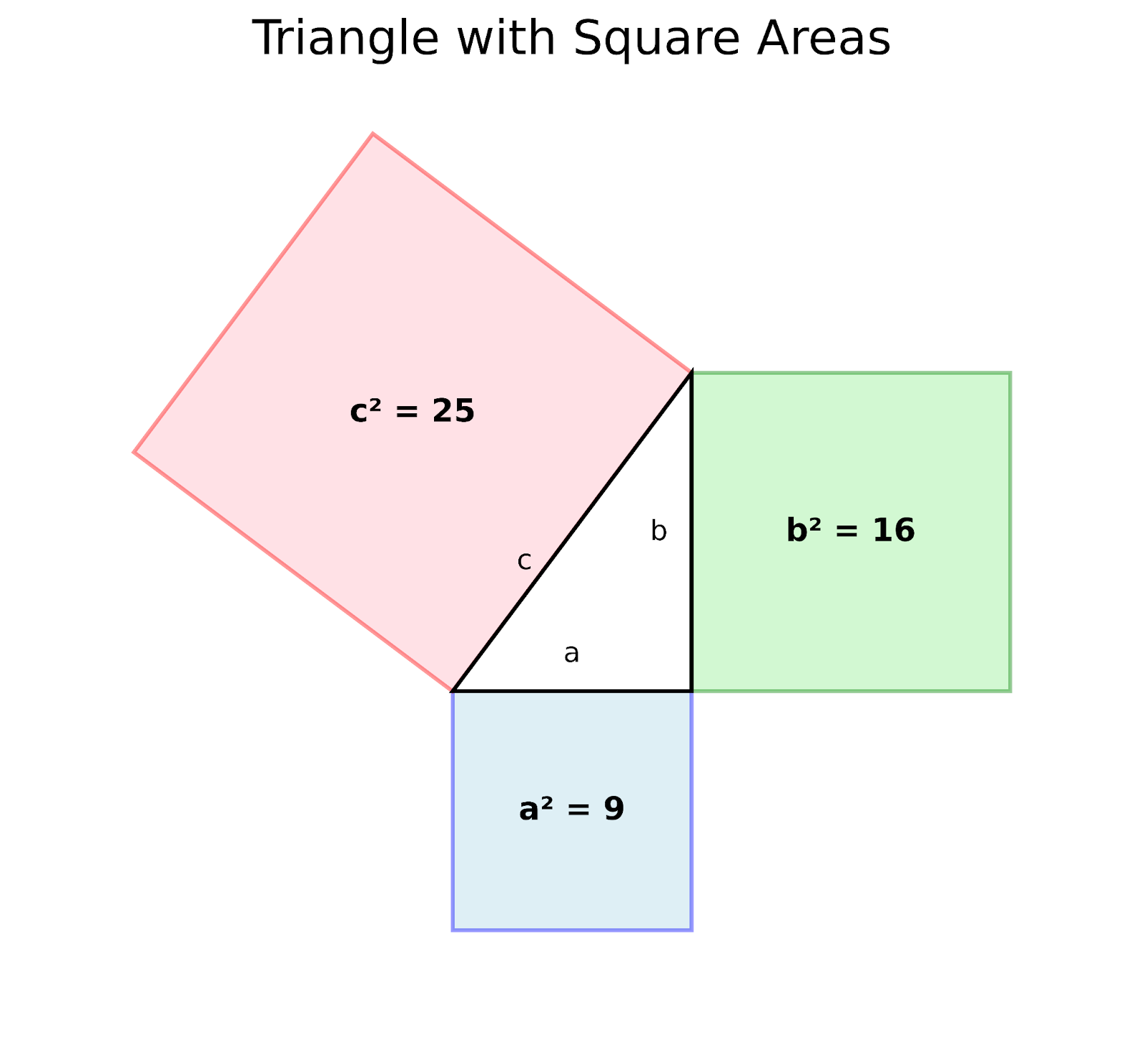
Demostración geométrica del teorema de Pitágoras. Imagen del autor

La construcción comienza con un triángulo rectángulo donde: 

1. Los dos lados perpendiculares se denominan "a" y "b" (los catetos)
2. El lado más largo "c" es la hipotenusa
3. Se dibujan cuadrados a lo largo de cada lado del triángulo

Los cuadrados coloreados representan visualmente: 

• El cuadrado azul tiene un área ^a² o 9
• El cuadrado verde tiene un área ^b² o 16
• El cuadrado rosa tiene un área ^c² o 25

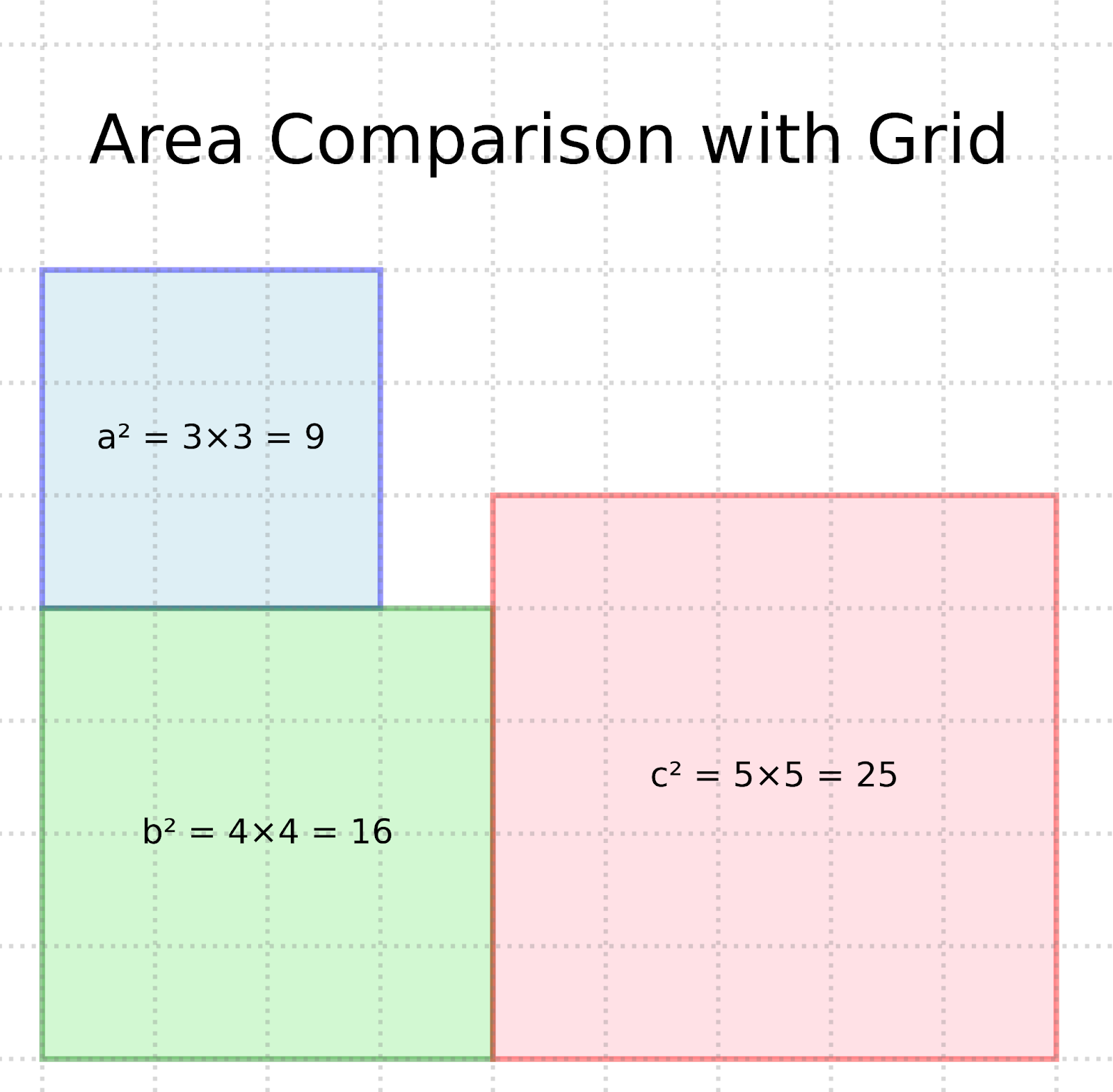
Representación en cuadrícula del teorema de Pitágoras. Imagen del autor

La visualización de la cuadrícula demuestra la igualdad ^a² + ^b² = ^c² mostrando que: 

• El cuadrado azul mide 3×3 = 9 unidades cuadradas (^a²) 
• El cuadrado verde mide 4×4 = 16 unidades cuadradas (^b²) 
• Juntas, estas superficies suman 25 unidades cuadradas 
• El cuadrado rosa mide 5×5 = 25 unidades cuadradas (^c²) 

La brillantez de esta demostración reside en su claridad visual: puedes ver literalmente que el área del cuadrado de la hipotenusa es igual a la suma de las áreas de los otros dos cuadrados: 9 + 16 = 25.

Otros enfoques geométricos notables

La verdad geométrica del teorema puede demostrarse mediante otros métodos, entre ellos:

• Prueba del semicírculo: Utilizando la relación entre los semicírculos trazados en cada lado del triángulo rectángulo
• Método del paralelogramo: Mostrar la equivalencia de áreas mediante rectas paralelas y triángulos semejantes
• Prueba basada en la similitud: Utilizando las propiedades de los triángulos semejantes creados por la altitud a la hipotenusa

Demostraciones algebraicas del teorema de Pitágoras

El ámbito algebraico ofrece enfoques igualmente diversos para demostrar este teorema. Aquí tienes una elegante demostración, seguida de referencias a otros métodos algebraicos significativos.

Enfoque de triángulos similares

Esta prueba aprovecha el poder de las relaciones proporcionales: 

1. Empieza con un triángulo rectángulo de altura h y base b
2. Expresa la hipotenusa c mediante la altura y la base: ^c² = ^h² + ^b²
3. Utiliza triángulos semejantes para demostrar que los lados correspondientes son proporcionales
4. Mediante manipulación algebraica, llega a ^a² + ^b² = ^c²

Otras demostraciones algebraicas

El teorema puede verificarse mediante diversas técnicas algebraicas, entre ellas:

• Identidad pitagórica: Utilizando relaciones trigonométricas (^cos²θ+ ^sin²θ= 1)
• Expansión cuadrática: Expansión de cuadrados perfectos y diferencia de cuadrados
• Álgebra vectorial: Utilizar las propiedades del producto punto y las magnitudes vectoriales
• Derivación de la fórmula de la distancia: Trabajar hacia atrás a partir de la fórmula de la distancia en geometría de coordenadas
• Métodos matriciales: Utilizar el álgebra lineal y las matrices de transformación

Cada método de demostración, ya sea geométrico o algebraico, ilumina diferentes aspectos de esta relación fundamental, contribuyendo a nuestra comprensión más profunda de la verdad matemática. Estos diversos enfoques también demuestran la naturaleza interconectada de las distintas ramas de las matemáticas, desde la geometría básica hasta el álgebra avanzada.

Otras pruebas notables

El teorema de Pitágoras ha inspirado cientos de pruebas únicas a lo largo de la historia, cada una de las cuales ofrece nuevas perspectivas:

1. La prueba de Einstein: Un Albert Einstein adolescente descubrió una demostración utilizando las propiedades de los triángulos semejantes
2. La prueba del presidente Garfield (1876): James Garfield, vigésimo presidente de EE.UU., creó una prueba utilizando un trapecio
3. The Johnson-Jackson Proof (2023): Dos estudiantes de último curso de secundaria, Calcea Johnson y Ne'Kiya Jackson, de la Academia St. Mary de Nueva Orleans, han hecho historia en las matemáticas al desarrollar una nueva prueba utilizando la trigonometría. Su enfoque innovador suscitó debates sobre los fundamentos de las pruebas matemáticas y las relaciones entre la geometría y la trigonometría. El logro demuestra que, incluso después de miles de años, este teorema fundamental sigue aportando nuevos conocimientos matemáticos.

Triples pitagóricos y generalizaciones

¿Qué son los triples pitagóricos?

Al explorar el teorema de Pitágoras, descubrimos conjuntos de tres números enteros que satisfacen la ecuación ^a² + ^b² = ^c². Estos conjuntos se llaman triples pitagóricos. El ejemplo más familiar es (3, 4, 5), que quizá reconozcas de nuestra historia inicial sobre los constructores egipcios.

Veamos algunos triples pitagóricos comunes:

• (3, 4, 5): 3^² + 4^² = 9 + 16 = 25 = 5^²
• (5, 12, 13): 5^² + 12^² = 25 + 144 = 169 = 13^²
• (8, 15, 17): 8^² + 15^² = 64 + 225 = 289 = 17^²

Curiosamente, cualquier triple pitagórico multiplicado por un número entero crea otro triple válido. Por ejemplo, duplicando (3, 4, 5) obtenemos (6, 8, 10).

Generalizaciones del teorema de Pitágoras

El teorema de Pitágoras se extiende más allá de los triángulos rectángulos de forma fascinante:

1. Dimensiones superiores: El concepto se expande a tres dimensiones como la fórmula de la distancia en el espacio 3D: ^d² = ^x² + ^y² + ^z²
2. Geometría no euclidiana: En geometría esférica, como el cálculo de distancias en la superficie terrestre, el teorema se transforma en nuevas relaciones en las que la suma de los cuadrados no siempre es igual. Como se muestra en la siguiente ilustración, el teorema de Pitágoras funciona bien en superficies planas. Pero, cuando pasamos a superficies curvas, necesitamos una fórmula distinta llamada ley esférica de los cosenos: cos(c) = cos(a)cos(b) + sen(a)sen(b)cos(C), donde c es la longitud del lado y C es el ángulo opuesto a él.

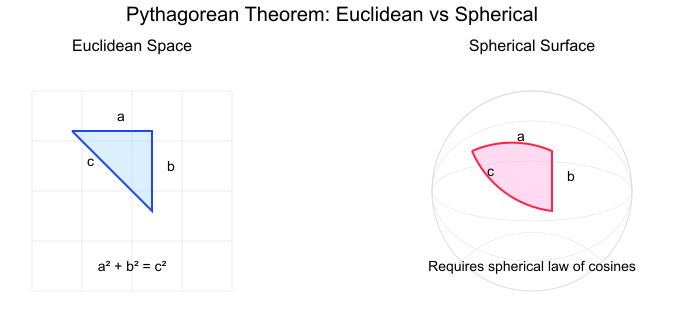
Teorema de Pitágoras en espacios euclidianos y no euclidianos. Imagen del autor

3. La Ley de los Cosenos: Esta generalización sirve para cualquier triángulo, no sólo los rectángulos: ^c² = ^a² + ^b² - 2ab cos(C) Cuando el ángulo C es de 90°, cos(C) = 0, y volvemos a nuestro conocido teorema de Pitágoras.

Estas generalizaciones revelan cómo una simple relación entre los lados de un triángulo rectángulo abre puertas a la comprensión del espacio, la distancia y la geometría en contextos más amplios.

El Teorema de Pitágoras en Programación y Ciencia de Datos

Medidas de distancia en el aprendizaje automático

El teorema de Pitágoras constituye la base de la distancia euclídea, una métrica muy utilizada en el aprendizaje automático. Cuando un algoritmo necesita determinar lo similares o diferentes que son dos puntos de datos, suele utilizar este principio. Aquí exploraremos una implementación básica, y para una exploración completa de las métricas de distancia y sus aplicaciones, encontrarás nuestro Comprender la distancia euclídea: De la teoría a la práctica especialmente valioso.

Considera un ejemplo sencillo: comparar casas en función de su tamaño (eje x) y su precio (eje y). La distancia euclidiana entre dos casas en este espacio de características nos dice lo parecidas que son:

import numpy as np

def euclidean_distance(point1, point2):
    return np.sqrt(np.sum((point1 - point2) ** 2))

# Example: Two houses
house1 = np.array([1500, 300000])  # 1500 sq ft, $300,000
house2 = np.array([2000, 450000])  # 2000 sq ft, $450,000
distance = euclidean_distance(house1, house2)

Esta métrica de distancia resulta especialmente potente en los sistemas de recomendación y en los algoritmos de agrupación, donde ayuda a identificar patrones y a agrupar elementos similares. Por ejemplo, Netflix utiliza cálculos de distancia similares para sugerir películas en función de los patrones de visionado, y las plataformas de comercio electrónico los emplean para recomendar productos en función de las preferencias del usuario.

Aplicaciones en álgebra lineal

El teorema nos ayuda a comprender las operaciones vectoriales, sobre todo a calcular magnitudes vectoriales y determinar la ortogonalidad:

def vector_magnitude(vector):
    """Calculate the length (magnitude) of a vector"""
    return np.sqrt(np.sum(vector ** 2))

# Example: 3D vector
vector = np.array([3, 4, 5])
magnitude = vector_magnitude(vector)

Este concepto se extiende a las redes neuronales, en las que el cálculo de las magnitudes vectoriales ayuda:

• Normalizar las características de entrada
• Cálculo de magnitudes de gradiente durante el entrenamiento
• Medición de las distribuciones del peso del modelo

Estas operaciones vectoriales forman la base de las arquitecturas modernas de aprendizaje profundo, donde la capacidad de medir y manipular espacios de alta dimensión se convierte en algo fundamental para tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y los sistemas autónomos. La elegante simplicidad del teorema de Pitágoras sigue impulsando algunas de las aplicaciones de IA más sofisticadas de la actualidad.

Optimización en algoritmos

El teorema de Pitágoras es fundamental en los algoritmos de optimización, especialmente en el descenso gradiente. Cuando buscamos la ruta más corta hacia un valor mínimo, a menudo nos basamos en cálculos de distancia informados por este teorema. Esta técnica de optimización impulsa el aprendizaje automático moderno. Si estás deseando profundizar en el conocimiento de su mecánica y aplicaciones, nuestro tutorial Gradient Descent in Machine Learning proporciona una amplia exploración de esta potente técnica matemática. 

Las aplicaciones de optimización del teorema se extienden a diversos ámbitos. En los problemas de flujo de red, ayuda a determinar las rutas óptimas para la transmisión de datos. Al minimizar distancias en problemas espaciales, el teorema guía a los algoritmos para encontrar soluciones eficientes. En el aprendizaje automático, es especialmente valioso para optimizar los parámetros del modelo durante el entrenamiento, ayudando a los algoritmos a converger en las predicciones más precisas posibles.

Conclusión

El teorema de Pitágoras tiende un puente entre la sabiduría antigua y la innovación moderna. Desde los constructores egipcios que creaban ángulos rectos perfectos hasta los científicos de datos que calculan distancias en espacios de alta dimensión, esta relación matemática sigue revelando nuevas aplicaciones. La sencilla fórmula ^a² + ^b² = ^c² abre las puertas a la comprensión de complejas verdades geométricas, que conducen desde mediciones básicas de triángulos hasta sofisticados algoritmos de aprendizaje automático.

Si quieres dar el siguiente paso en la aplicación de estas ideas, nuestro curso Diseño de flujos de trabajo de aprendizaje automático en Python proporciona una guía práctica para integrar principios matemáticos como éstos en los conductos de aprendizaje automático del mundo real.