Teorema de Pitágoras: Explorando a relação fundamental da geometria

O teorema de Pitágoras é mais do que apenas um elemento básico da geometria do ensino médio; ele é a pedra fundamental da álgebra linear, formando a base para a compreensão das normas vetoriais, da ortogonalidade e das projeções em espaços de dimensões maiores. Esses conceitos não são apenas fundamentais para a teoria, mas também têm aplicações práticas na ciência de dados, onde sustentam algoritmos de aprendizado de máquina e redução de dimensionalidade.

Neste artigo, começarei pelo início e analisarei os conceitos básicos do teorema de Pitágoras e, aos poucos, avançarei para as aplicações mais avançadas e menos conhecidas do teorema em dimensões mais altas, incluindo sua função na análise de conjuntos de dados complexos, otimização de modelos de aprendizado de máquina e visualização de relações geométricas em fluxos de trabalho de ciência de dados. Se você deseja explorar mais essas conexões e ver como elas se aplicam na prática, nosso curso Álgebra Linear para Ciência de Dados em R oferece uma abordagem prática para unir a teoria aos problemas de dados do mundo real.

Introdução ao teorema de Pitágoras

Imagine o Egito antigo, onde os arquitetos e construtores enfrentavam um desafio irresistível: criar ângulos retos perfeitos para suas estruturas magníficas. Sua solução engenhosa? Uma corda simples marcada com 12 seções iguais. Ao formar um triângulo com lados de 3, 4 e 5 unidades, eles descobriram que poderiam criar ângulos retos perfeitos todas as vezes.

O teorema de Pitágoras é uma das relações mais elegantes e práticas da matemática. Embora tradicionalmente creditado ao antigo matemático grego Pitágoras (570-495 a.C.), as evidências sugerem que esse princípio fundamental era conhecido por várias civilizações antigas, incluindo os babilônios e os chineses, mais de um milênio antes de Pitágoras prová-lo sistematicamente.

A fórmula do teorema de Pitágoras

O teorema de Pitágoras expressa uma relação clara: em qualquer triângulo retângulo, o quadrado do comprimento da hipotenusa (c) é igual à soma dos quadrados dos outros dois lados (a e b). Essa relação aparece na famosa equação:

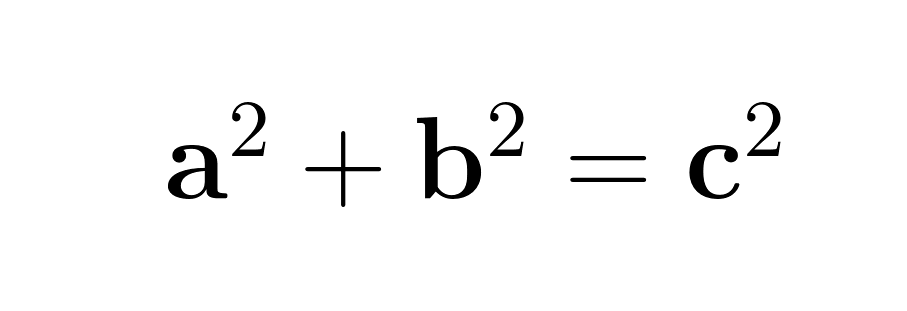
Onde:

• a e b são os comprimentos das duas pernas (os lados adjacentes ao ângulo reto)
• c é o comprimento da hipotenusa (o lado mais longo, oposto ao ângulo reto)

Provas do teorema de Pitágoras

Compreender as diferentes provas do teorema de Pitágoras ajuda a revelar por que essa relação é verdadeira em toda a matemática. Vamos explorar algumas abordagens diferentes para provar esse teorema.

Provas geométricas do teorema de Pitágoras

Ao longo da história, os matemáticos desenvolveram inúmeras provas geométricas do teorema de Pitágoras, cada uma oferecendo percepções únicas sobre essa relação fundamental. Vamos explorar uma das abordagens mais impressionantes visualmente, reconhecendo a grande variedade de demonstrações geométricas disponíveis.

A prova de construção quadrada

Uma prova geométrica clássica, popularizada em Euclid's Elements (Elementosde Euclides ), continua sendo uma das demonstrações visualmente mais atraentes do teorema. Veja como isso funciona:

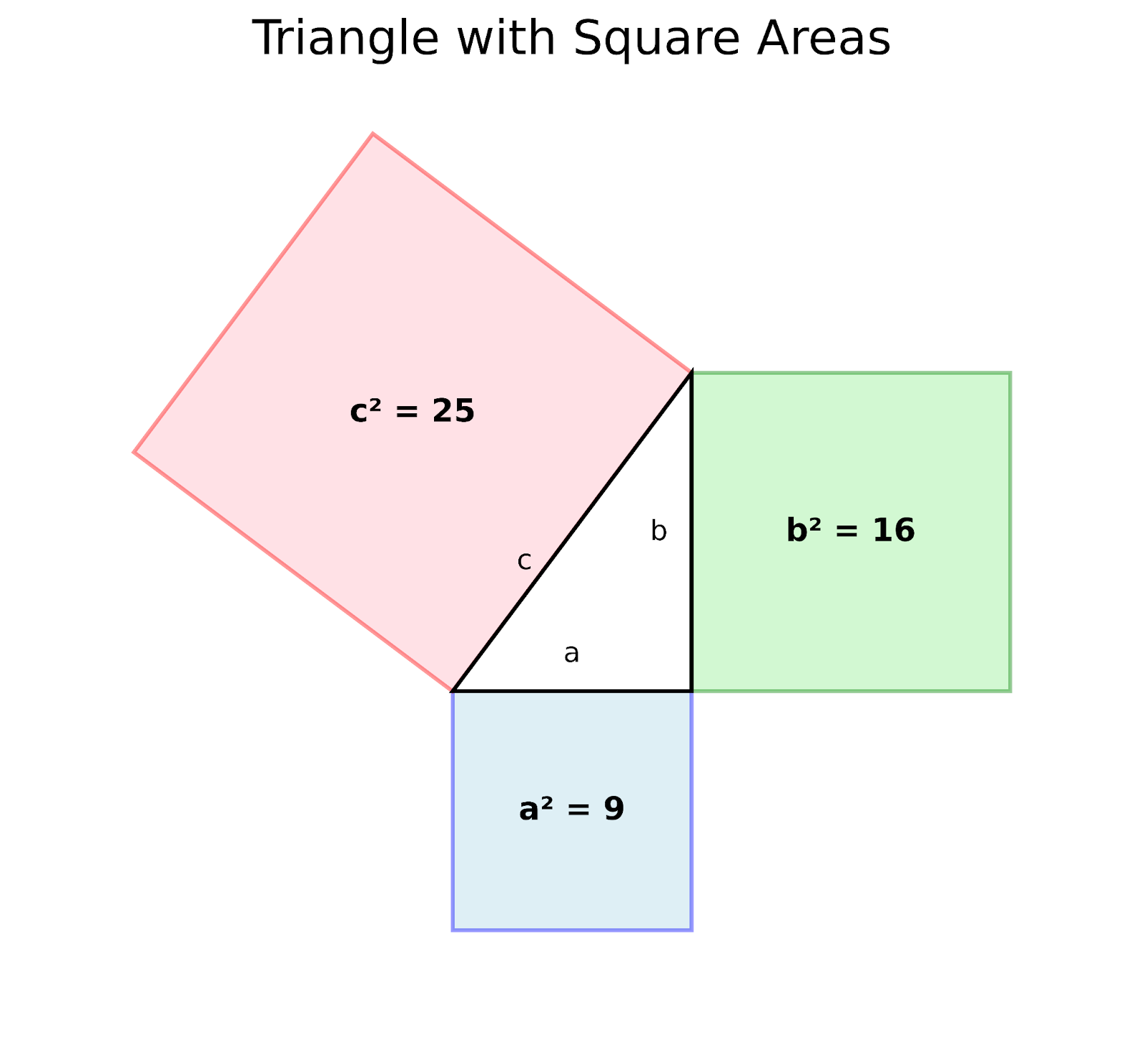
Prova geométrica do teorema de Pitágoras. Imagem por autor

A construção começa com um triângulo retângulo em que você tem um triângulo retângulo: 

1. Os dois lados perpendiculares são rotulados como 'a' e 'b' (as pernas)
2. O lado mais longo "c" é a hipotenusa
3. Os quadrados são desenhados ao longo de cada lado do triângulo

Os quadrados coloridos representam visualmente: 

• O quadrado azul tem área ^a² ou 9
• O quadrado verde tem área ^b² ou 16
• O quadrado rosa tem área ^c² ou 25

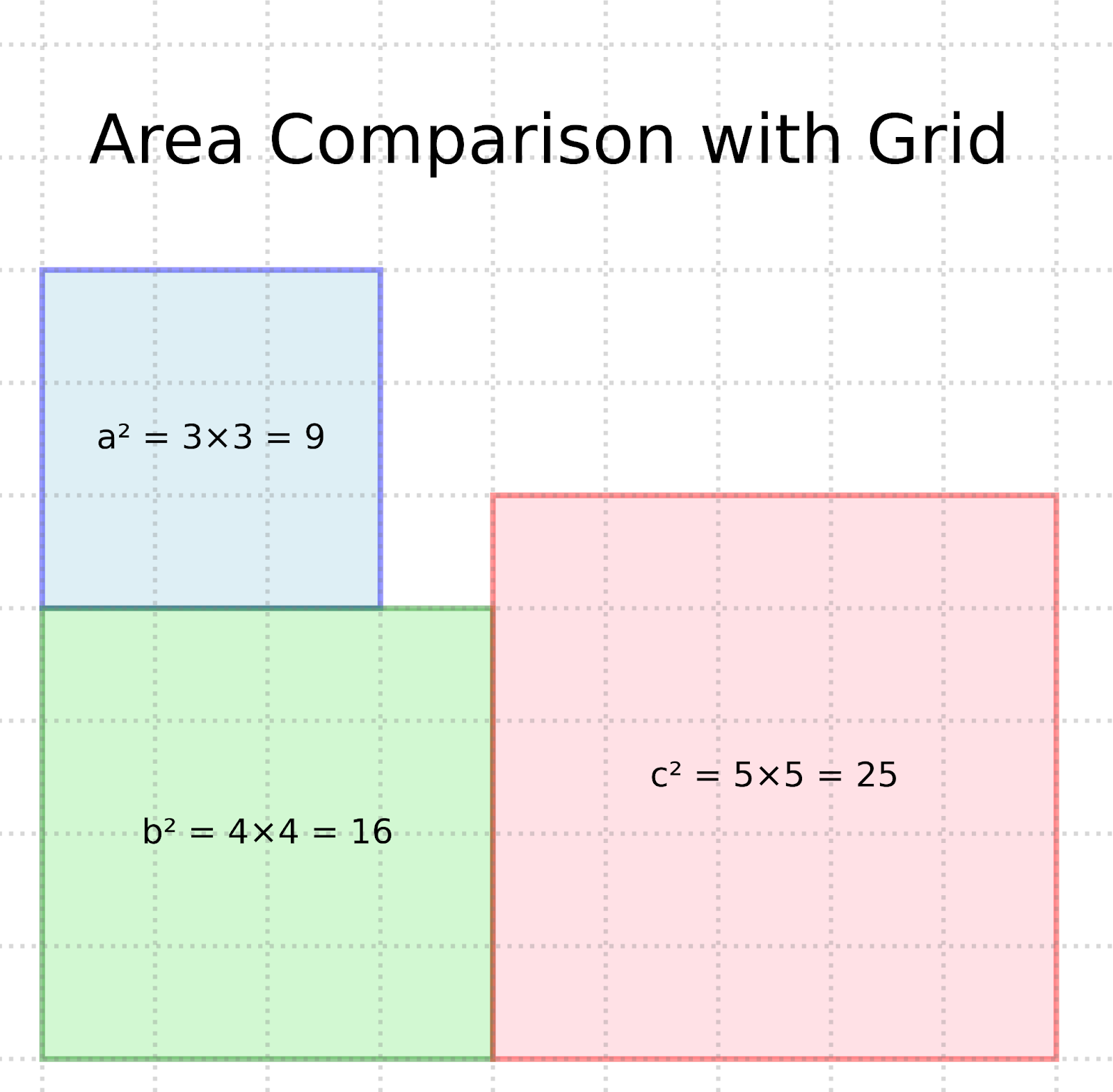
Representação em grade do teorema de Pitágoras. Imagem por autor

A visualização da grade demonstra a igualdade ^a² + ^b² = ^c², mostrando que 

• O quadrado azul mede 3×3 = 9 unidades quadradas (^a²) 
• O quadrado verde mede 4×4 = 16 unidades quadradas (^b²) 
• Juntas, essas áreas somam 25 unidades quadradas 
• O quadrado rosa mede 5×5 = 25 unidades quadradas (^c²) 

O brilhantismo dessa prova está em sua clareza visual - você pode literalmente ver que a área do quadrado na hipotenusa é igual à soma das áreas dos outros dois quadrados: 9 + 16 = 25.

Outras abordagens geométricas notáveis

A verdade geométrica do teorema pode ser demonstrada por meio de vários outros métodos, inclusive:

• Prova de semicírculo: Usando a relação entre os semicírculos desenhados em cada lado do triângulo retângulo
• Método do paralelogramo: Mostrar a equivalência de áreas usando linhas paralelas e triângulos semelhantes
• Prova baseada em similaridade: Usando as propriedades de triângulos semelhantes criados pela altitude da hipotenusa

Provas algébricas do teorema de Pitágoras

O domínio algébrico oferece abordagens igualmente diversas para provar esse teorema. Aqui está uma demonstração elegante, seguida de referências a outros métodos algébricos significativos.

Abordagem de triângulos semelhantes

Essa prova aproveita o poder das relações proporcionais: 

1. Comece com um triângulo retângulo com altura h e base b
2. Expresse a hipotenusa c usando a altura e a base: ^c² = ^h² + ^b²
3. Use triângulos semelhantes para mostrar que os lados correspondentes são proporcionais
4. Por meio de manipulação algébrica, você chegará a ^a² + ^b² = ^c²

Outras demonstrações algébricas

O teorema pode ser verificado por meio de várias técnicas algébricas, incluindo:

• Identidade pitagórica: Usando relações trigonométricas (^cos²θ+ ^sin²θ= 1)
• Expansão quadrática: Expansão de quadrados perfeitos e diferença de quadrados
• Álgebra vetorial: Utilizar as propriedades do produto escalar e as magnitudes vetoriais
• Derivação da fórmula da distância: Trabalhando de trás para frente a partir da fórmula de distância na geometria de coordenadas
• Métodos de matriz: Usando álgebra linear e matrizes de transformação

Cada método de prova, seja ele geométrico ou algébrico, ilumina diferentes aspectos dessa relação fundamental, contribuindo para nossa compreensão mais profunda da verdade matemática. Essas várias abordagens também demonstram a natureza interconectada de diferentes ramos da matemática, desde a geometria básica até a álgebra avançada.

Outras provas notáveis

O teorema de Pitágoras inspirou centenas de provas únicas ao longo da história, cada uma oferecendo novas percepções:

1. Prova de Einstein: Albert Einstein, ainda adolescente, descobriu uma prova usando as propriedades de triângulos semelhantes
2. Prova do Presidente Garfield (1876): James Garfield, o 20º presidente dos EUA, criou uma prova usando um trapézio
3. The Johnson-Jackson Proof (2023): Duas alunas do último ano do ensino médio, Calcea Johnson e Ne'Kiya Jackson, da St. Mary's Academy em Nova Orleans, fizeram história na matemática ao desenvolver uma nova prova usando trigonometria. Sua abordagem inovadora gerou discussões sobre os fundamentos das provas matemáticas e as relações entre geometria e trigonometria. A conquista demonstra que, mesmo depois de milhares de anos, esse teorema fundamental continua a produzir novas percepções matemáticas.

Triplos pitagóricos e generalizações

O que são os triplos pitagóricos?

Ao explorar o teorema de Pitágoras, descobrimos conjuntos de três números inteiros que satisfazem a equação ^a² + ^b² = ^c². Esses conjuntos são chamados de triplos pitagóricos. O exemplo mais familiar é (3, 4, 5), que você talvez reconheça da nossa história inicial sobre os construtores egípcios.

Vamos dar uma olhada em alguns triplos pitagóricos comuns:

• (3, 4, 5): 3^² + 4^² = 9 + 16 = 25 = 5^²
• (5, 12, 13): 5^² + 12^² = 25 + 144 = 169 = 13^²
• (8, 15, 17): 8^² + 15^² = 64 + 225 = 289 = 17^²

É interessante notar que qualquer triplo pitagórico multiplicado por um número inteiro cria outro triplo válido. Por exemplo, ao dobrar (3, 4, 5), você obtém (6, 8, 10).

Generalizações do teorema de Pitágoras

O teorema de Pitágoras vai além dos triângulos retângulos de maneiras fascinantes:

1. Dimensões superiores: O conceito se expande para três dimensões como a fórmula da distância no espaço 3D: ^d² = ^x² + ^y² + ^z²
2. Geometria não euclidiana: Na geometria esférica, como o cálculo de distâncias na superfície da Terra, o teorema se transforma em novas relações em que a soma dos quadrados nem sempre é igual. Conforme mostrado na ilustração abaixo, o teorema de Pitágoras funciona bem em superfícies planas. Mas, quando passamos para superfícies curvas, precisamos de uma fórmula diferente chamada lei esférica dos cossenos: cos(c) = cos(a)cos(b) + sin(a)sin(b)cos(C), em que c é o comprimento do lado e C é o ângulo oposto a ele.

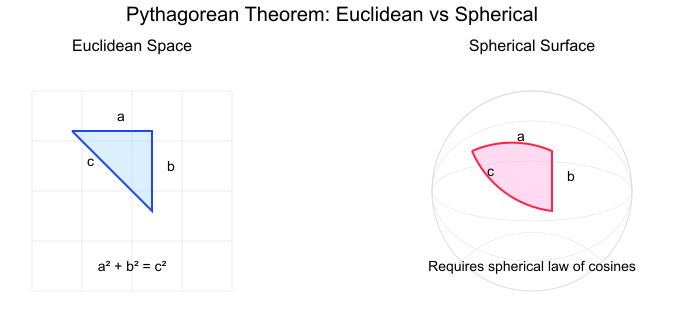
Teorema de Pitágoras em espaços euclidianos e não euclidianos. Imagem do autor

3. A lei dos cossenos: Essa generalização funciona para qualquer triângulo, não apenas para os triângulos retângulos: ^c² = ^a² + ^b² - 2ab cos(C) Quando o ângulo C é de 90°, cos(C) = 0, e você obtém o conhecido teorema de Pitágoras.

Essas generalizações revelam como uma simples relação entre os lados de um triângulo retângulo abre portas para a compreensão do espaço, da distância e da geometria em contextos mais amplos.

O teorema de Pitágoras na programação e na ciência de dados

Medidas de distância no aprendizado de máquina

O teorema de Pitágoras forma a base da distância euclidiana, uma métrica amplamente usada no aprendizado de máquina. Quando um algoritmo precisa determinar a semelhança ou a diferença entre dois pontos de dados, ele geralmente usa esse princípio. Vamos explorar uma implementação básica aqui e, para uma exploração completa das métricas de distância e suas aplicações, você encontrará nosso site Understanding Euclidean Distance: From Theory to Practice particularmente valioso.

Considere um exemplo simples: comparar casas com base em seu tamanho (eixo x) e preço (eixo y). A distância euclidiana entre duas casas nesse espaço de recursos nos diz o quanto elas são semelhantes:

import numpy as np

def euclidean_distance(point1, point2):
    return np.sqrt(np.sum((point1 - point2) ** 2))

# Example: Two houses
house1 = np.array([1500, 300000])  # 1500 sq ft, $300,000
house2 = np.array([2000, 450000])  # 2000 sq ft, $450,000
distance = euclidean_distance(house1, house2)

Essa métrica de distância torna-se particularmente poderosa em sistemas de recomendação e algoritmos de agrupamento, onde ajuda a identificar padrões e agrupar itens semelhantes. Por exemplo, a Netflix usa cálculos de distância semelhantes para sugerir filmes com base em padrões de visualização, e as plataformas de comércio eletrônico os utilizam para recomendar produtos com base nas preferências do usuário.

Aplicações em álgebra linear

O teorema nos ajuda a entender as operações vetoriais, especialmente no cálculo de magnitudes vetoriais e na determinação da ortogonalidade:

def vector_magnitude(vector):
    """Calculate the length (magnitude) of a vector"""
    return np.sqrt(np.sum(vector ** 2))

# Example: 3D vector
vector = np.array([3, 4, 5])
magnitude = vector_magnitude(vector)

Esse conceito se estende às redes neurais, nas quais o cálculo das magnitudes dos vetores ajuda:

• Normalização de recursos de entrada
• Cálculo de magnitudes de gradiente durante o treinamento
• Medição das distribuições de peso do modelo

Essas operações vetoriais formam a base das arquiteturas modernas de aprendizagem profunda, em que a capacidade de medir e manipular espaços de alta dimensão torna-se fundamental para tarefas como reconhecimento de imagens, processamento de linguagem natural e sistemas autônomos. A simplicidade elegante do teorema de Pitágoras continua a alimentar alguns dos aplicativos de IA mais sofisticados da atualidade.

Otimização em algoritmos

O teorema de Pitágoras é fundamental para os algoritmos de otimização, especialmente na descida de gradiente. Quando buscamos o caminho mais curto para um valor mínimo, frequentemente dependemos de cálculos de distância informados por esse teorema. Essa técnica de otimização impulsiona o aprendizado de máquina moderno. Se você deseja aprofundar seu conhecimento sobre sua mecânica e aplicações, nosso tutorial Gradient Descent in Machine Learning oferece uma ampla exploração dessa poderosa técnica matemática. 

As aplicações de otimização do teorema se estendem por vários domínios. Em problemas de fluxo de rede, ele ajuda a determinar os caminhos ideais para a transmissão de dados. Ao minimizar as distâncias em problemas espaciais, o teorema orienta os algoritmos a encontrar soluções eficientes. No aprendizado de máquina, ele é particularmente valioso para otimizar os parâmetros do modelo durante o treinamento, ajudando os algoritmos a convergir para as previsões mais precisas possíveis.

Conclusão

O teorema de Pitágoras une a sabedoria antiga à inovação moderna. De construtores egípcios criando ângulos retos perfeitos a cientistas de dados calculando distâncias em espaços de alta dimensão, essa relação matemática continua a revelar novas aplicações. A fórmula simples ^a² + ^b² = ^c² abre as portas para a compreensão de verdades geométricas complexas, desde medições básicas de triângulos até algoritmos sofisticados de aprendizado de máquina.

Se você deseja dar o próximo passo na aplicação dessas ideias, nosso curso Projetando fluxos de trabalho de aprendizado de máquina em Python oferece um guia prático para integrar princípios matemáticos como esses em pipelines de aprendizado de máquina do mundo real.