Théorème de Pythagore : Explorer la relation fondamentale de la géométrie

Le théorème de Pythagore est plus qu'un simple élément de base de la géométrie au lycée ; c'est une pierre angulaire de l'algèbre linéaire, qui constitue la base de la compréhension des normes vectorielles, de l'orthogonalité et des projections dans des espaces de plus grande dimension. Ces concepts sont non seulement fondamentaux pour la théorie, mais ils ont également des applications pratiques dans la science des données, où ils sous-tendent les algorithmes d'apprentissage automatique et de réduction de la dimensionnalité.

Dans cet article, je commencerai par le début et passerai en revue les bases du théorème de Pythagore, puis j'aborderai progressivement les applications plus avancées et moins connues du théorème dans des dimensions supérieures, notamment son rôle dans l'analyse d'ensembles de données complexes, l'optimisation des modèles d'apprentissage automatique et la visualisation des relations géométriques dans les flux de travail de la science des données. Si vous souhaitez approfondir ces liens et voir comment ils s'appliquent en pratique, notre cours d' algèbre linéaire pour la science des données en R propose une approche pratique pour faire le lien entre la théorie et les problèmes de données du monde réel.

Introduction au théorème de Pythagore

Imaginez l'Égypte ancienne, où les architectes et les bâtisseurs étaient confrontés à un défi de taille : créer des angles droits parfaits pour leurs magnifiques structures. Leur solution ingénieuse ? Une corde simple marquée de 12 sections égales. En formant un triangle avec des côtés de 3, 4 et 5 unités, ils ont découvert qu'ils pouvaient créer des angles droits parfaits à chaque fois.

Le théorème de Pythagore est l'une des relations mathématiques les plus élégantes et les plus pratiques. Bien qu'il soit traditionnellement attribué au mathématicien grec Pythagore (570-495 avant notre ère), il semble que ce principe fondamental ait été connu de plusieurs civilisations anciennes, dont les Babyloniens et les Chinois, plus d'un millénaire avant que Pythagore ne le démontre de manière systématique.

Formule du théorème de Pythagore

Le théorème de Pythagore exprime une relation claire : dans tout triangle droit, le carré de la longueur de l'hypoténuse (c) est égal à la somme des carrés des deux autres côtés (a et b). Cette relation apparaît dans la célèbre équation :

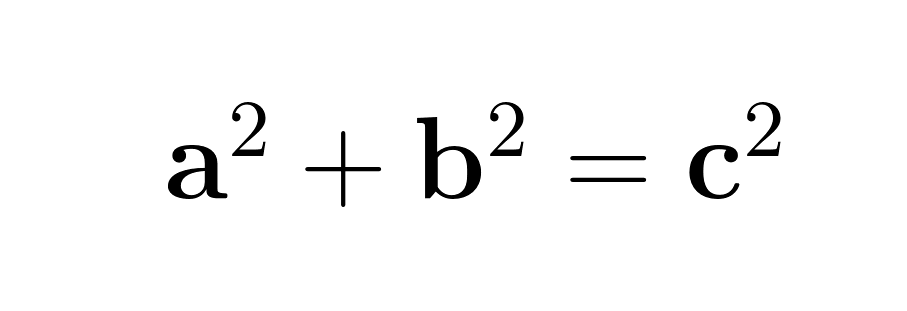
Où ?

• a et b sont les longueurs des deux branches (les côtés adjacents à l'angle droit)
• c est la longueur de l'hypoténuse (le côté le plus long, opposé à l'angle droit)

Preuves du théorème de Pythagore

Comprendre les différentes preuves du théorème de Pythagore permet de comprendre pourquoi cette relation est vraie dans toutes les mathématiques. Examinons quelques approches distinctes pour prouver ce théorème.

Preuves géométriques du théorème de Pythagore

Tout au long de l'histoire, les mathématiciens ont élaboré de nombreuses preuves géométriques du théorème de Pythagore, chacune offrant un aperçu unique de cette relation fondamentale. Explorons l'une des approches les plus visuellement frappantes, tout en reconnaissant la grande variété de démonstrations géométriques disponibles.

La preuve de construction carrée

Une preuve géométrique classique, popularisée dans les Éléments d'Euclide , reste l'une des démonstrations les plus visuellement convaincantes du théorème. Voici comment cela fonctionne :

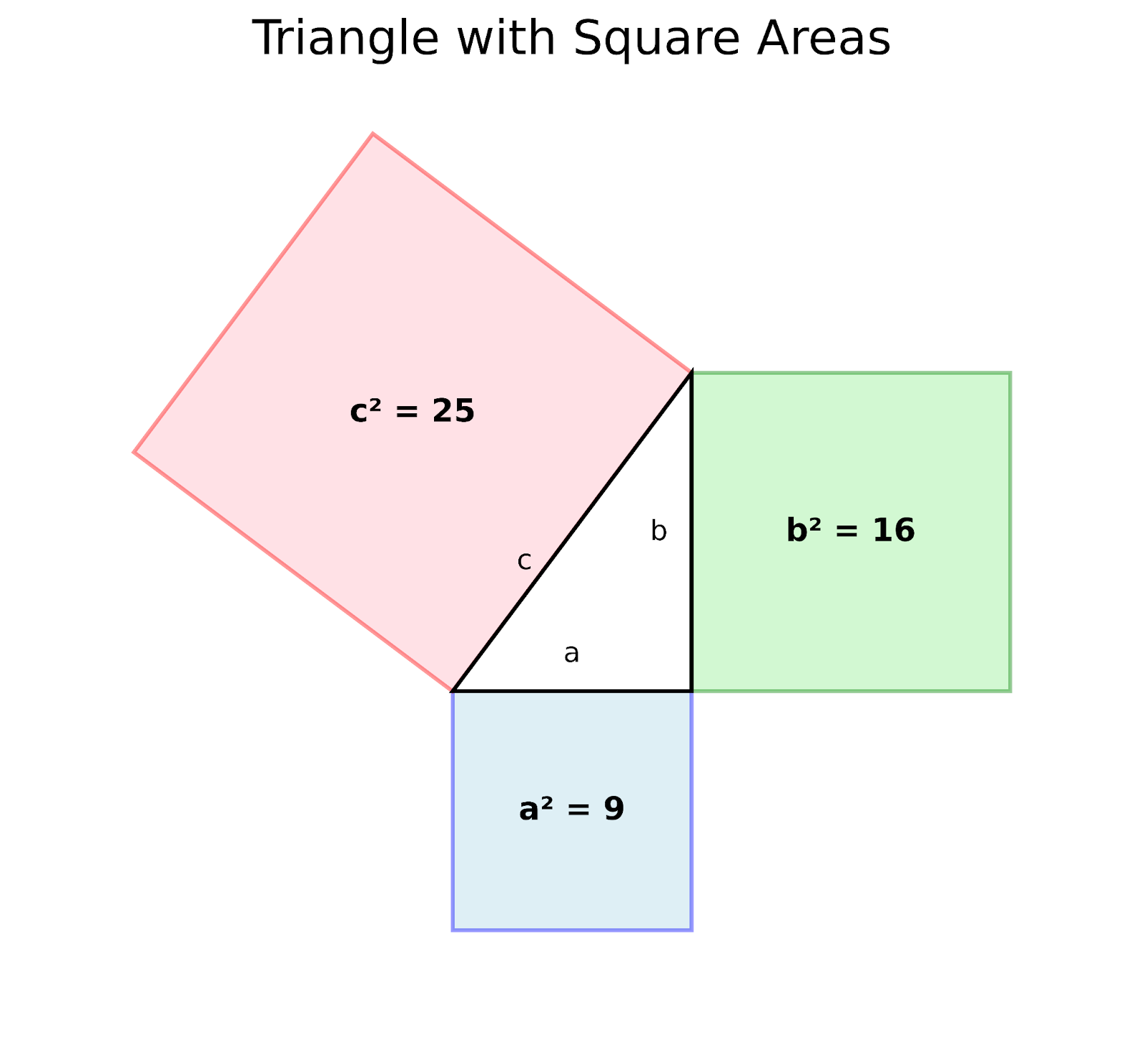
Preuve géométrique du théorème de Pythagore. Image par auteur

La construction commence par un triangle droit où : 

1. Les deux côtés perpendiculaires sont notés "a" et "b" (les jambes).
2. Le côté le plus long "c" est l'hypoténuse.
3. Des carrés sont tracés le long de chaque côté du triangle.

Les carrés colorés représentent visuellement : 

• Le carré bleu a une surface ^a² ou 9
• Le carré vert a une surface ^b² ou 16
• Le carré rose a une surface de ^c² ou 25

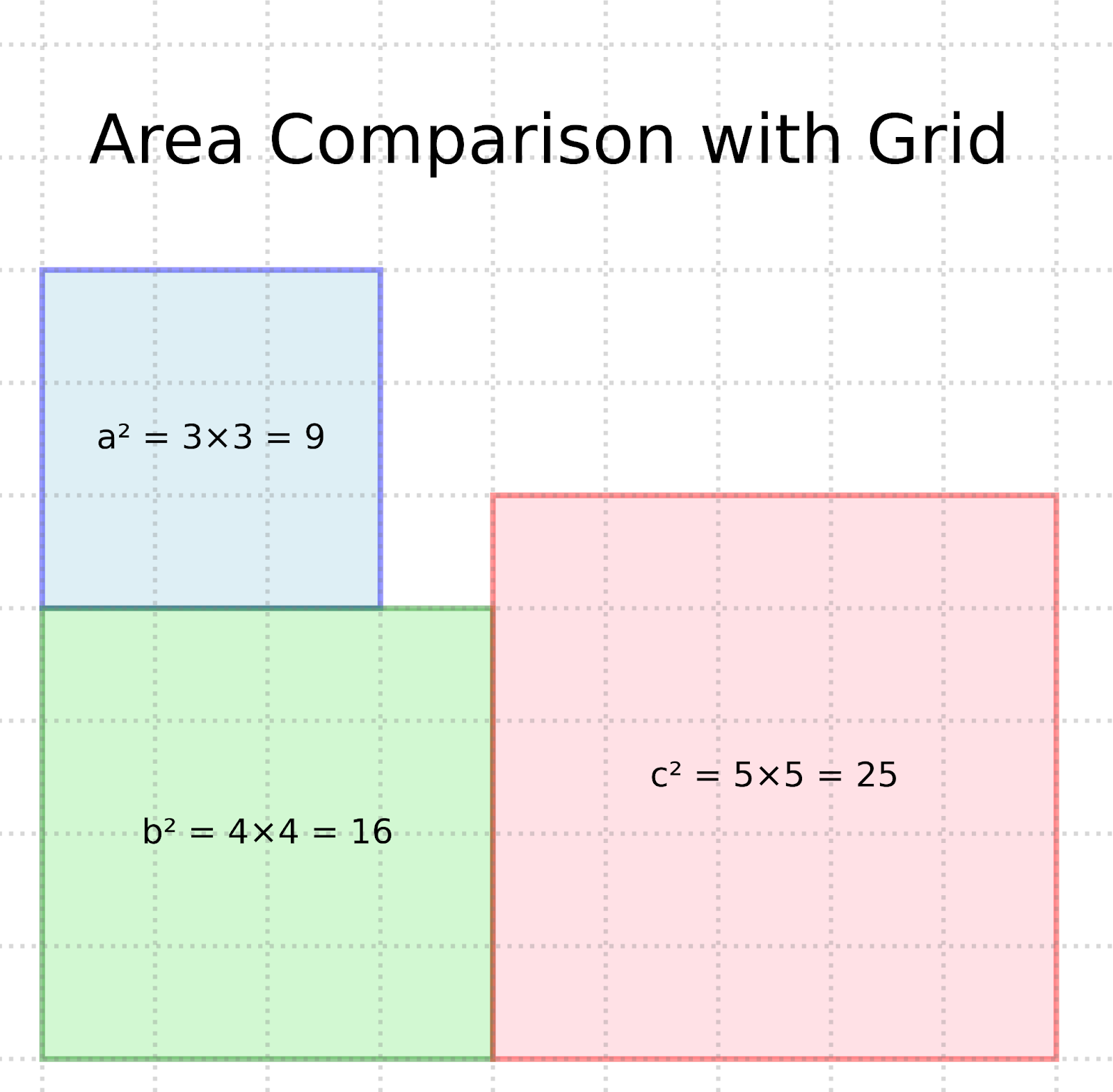
Représentation en grille du théorème de Pythagore. Image par auteur

La visualisation de la grille démontre l'égalité ^a² + ^b² = ^c² en montrant que : 

• Le carré bleu mesure 3×3 = 9 unités carrées (^a²) 
• Le carré vert mesure 4×4 = 16 unités carrées (^b²) 
• Ensemble, ces zones représentent 25 unités carrées 
• Le carré rose mesure 5×5 = 25 unités carrées (^c²) 

L'intérêt de cette preuve réside dans sa clarté visuelle - vous pouvez littéralement voir que l'aire du carré de l'hypoténuse est égale à la somme des aires des deux autres carrés : 9 + 16 = 25.

Autres approches géométriques notables

La vérité géométrique du théorème peut être démontrée par diverses autres méthodes, notamment :

• Preuve du demi-cercle: En utilisant la relation entre les demi-cercles tracés de chaque côté du triangle rectangle
• Méthode du parallélogramme: Montrer l'équivalence des aires à l'aide de lignes parallèles et de triangles semblables
• Preuve basée sur la similarité: Utilisation des propriétés des triangles semblables créés par l'altitude de l'hypoténuse

Preuves algébriques du théorème de Pythagore

Le domaine algébrique offre des approches tout aussi diverses pour prouver ce théorème. Voici une démonstration élégante, suivie de références à d'autres méthodes algébriques importantes.

Approche des triangles semblables

Cette preuve s'appuie sur la puissance des relations proportionnelles : 

1. Commencez par un triangle droit de hauteur h et de base b
2. Exprimez l'hypoténuse c à l'aide de la hauteur et de la base : ^c² = ^h² + ^b²
3. Utilisez des triangles semblables pour montrer que les côtés correspondants sont proportionnels.
4. Par une manipulation algébrique, obtenez ^a² + ^b² = ^c²

Autres démonstrations algébriques

Le théorème peut être vérifié à l'aide de diverses techniques algébriques, notamment :

• Identité de Pythagore: Utilisation des relations trigonométriques (^cos²θ+ ^sin²θ= 1)
• Développement quadratique: Extension de carrés parfaits et différence de carrés
• Algèbre vectorielle: Utilisation des propriétés du produit de points et des grandeurs vectorielles
• Formule de distance Dérivation: Travailler à rebours à partir de la formule de la distance en géométrie des coordonnées
• Méthodes matricielles: Utilisation de l'algèbre linéaire et des matrices de transformation

Chaque méthode de preuve, qu'elle soit géométrique ou algébrique, éclaire différents aspects de cette relation fondamentale, contribuant ainsi à une meilleure compréhension de la vérité mathématique. Ces différentes approches démontrent également la nature interconnectée des différentes branches des mathématiques, de la géométrie de base à l'algèbre avancée.

Autres preuves notables

Le théorème de Pythagore a inspiré des centaines de preuves uniques au cours de l'histoire, chacune apportant un éclairage nouveau :

1. La preuve d'Einstein: Un adolescent, Albert Einstein, a découvert une preuve utilisant les propriétés des triangles semblables.
2. La preuve du président Garfield (1876) : James Garfield, le 20e président des États-Unis, a créé une preuve à l'aide d'un trapèze.
3. L'épreuve Johnson-Jackson (2023) : Deux élèves de terminale, Calcea Johnson et Ne'Kiya Jackson de la St. Mary's Academy de la Nouvelle-Orléans, sont entrées dans l'histoire des mathématiques en élaborant une nouvelle preuve à l'aide de la trigonométrie. Leur approche innovante a suscité des discussions sur les fondements des preuves mathématiques et les relations entre la géométrie et la trigonométrie. Cette réussite démontre que, même après des milliers d'années, ce théorème fondamental continue d'apporter de nouvelles connaissances mathématiques.

Triples de Pythagore et généralisations

Que sont les triples de Pythagore ?

En explorant le théorème de Pythagore, nous découvrons des ensembles de trois nombres entiers qui satisfont à l'équation ^a² + ^b² = ^c². Ces ensembles sont appelés triples de Pythagore. L'exemple le plus familier est (3, 4, 5), que vous avez peut-être reconnu dans notre récit d'ouverture sur les bâtisseurs égyptiens.

Examinons quelques triples de Pythagore courants :

• (3, 4, 5): 3^² + 4^² = 9 + 16 = 25 = 5^²
• (5, 12, 13) : 5^² + 12^² = 25 + 144 = 169 = 13^²
• (8, 15, 17) : 8^² + 15^² = 64 + 225 = 289 = 17^²

Il est intéressant de noter que tout triple pythagoricien multiplié par un nombre entier crée un autre triple valide. Par exemple, en doublant (3, 4, 5), on obtient (6, 8, 10).

Généralisations du théorème de Pythagore

Le théorème de Pythagore s'étend au-delà des triangles droits de manière fascinante :

1. Dimensions supérieures : Le concept s'étend aux trois dimensions sous la forme de la formule de la distance dans l'espace 3D : ^d² = ^x² + ^y² + ^z²
2. Géométrie non euclidienne : En géométrie sphérique, comme pour le calcul des distances à la surface de la Terre, le théorème se transforme en de nouvelles relations où la somme des carrés n'est pas toujours égale. Comme le montre l'illustration ci-dessous, le théorème de Pythagore fonctionne bien sur les surfaces planes. Mais lorsque nous passons à des surfaces courbes, nous avons besoin d'une formule différente appelée la loi sphérique des cosinus : cos(c) = cos(a)cos(b) + sin(a)sin(b)cos(C), où c est la longueur du côté et C l'angle qui lui est opposé.

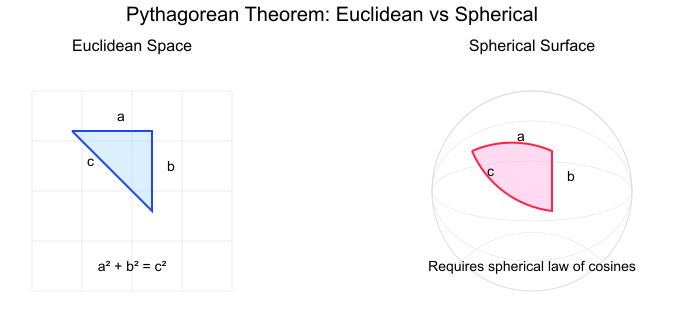
Théorème de Pythagore dans les espaces euclidiens et non euclidiens. Image par l'auteur

3. La loi des cosinus : Cette généralisation s'applique à tous les triangles, et pas seulement aux triangles rectangles : ^c² = ^a² + ^b² - 2ab cos(C) Lorsque l'angle C est de 90°, cos(C) = 0, et nous retrouvons le théorème de Pythagore que nous connaissons bien.

Ces généralisations révèlent comment une simple relation entre les côtés d'un triangle droit permet de comprendre l'espace, la distance et la géométrie dans des contextes plus larges.

Le théorème de Pythagore dans la programmation et la science des données

Mesures de distance dans l'apprentissage automatique

Le théorème de Pythagore est à la base de la distance euclidienne, une mesure largement utilisée dans l'apprentissage automatique. Lorsqu'un algorithme doit déterminer le degré de similitude ou de différence entre deux points de données, il utilise souvent ce principe. Pour une exploration complète des mesures de distance et de leurs applications, vous pouvez consulter notre site Understanding Euclidean Distance (Comprendre la distance euclidienne) : De la théorie à la pratique particulièrement précieux.

Prenons un exemple simple : comparer des maisons en fonction de leur taille (axe des x) et de leur prix (axe des y). La distance euclidienne entre deux maisons dans cet espace de caractéristiques nous indique leur degré de similitude :

import numpy as np

def euclidean_distance(point1, point2):
    return np.sqrt(np.sum((point1 - point2) ** 2))

# Example: Two houses
house1 = np.array([1500, 300000])  # 1500 sq ft, $300,000
house2 = np.array([2000, 450000])  # 2000 sq ft, $450,000
distance = euclidean_distance(house1, house2)

Cette mesure de distance devient particulièrement puissante dans les systèmes de recommandation et les algorithmes de regroupement, où elle permet d'identifier des modèles et de regrouper des éléments similaires. Par exemple, Netflix utilise des calculs de distance similaires pour suggérer des films en fonction des habitudes de visionnage, et les plateformes de commerce électronique s'en servent pour recommander des produits en fonction des préférences de l'utilisateur.

Applications en algèbre linéaire

Ce théorème nous aide à comprendre les opérations sur les vecteurs, en particulier à calculer les grandeurs vectorielles et à déterminer l'orthogonalité :

def vector_magnitude(vector):
    """Calculate the length (magnitude) of a vector"""
    return np.sqrt(np.sum(vector ** 2))

# Example: 3D vector
vector = np.array([3, 4, 5])
magnitude = vector_magnitude(vector)

Ce concept s'étend aux réseaux neuronaux, où le calcul de l'ampleur des vecteurs est utile :

• Normalisation des caractéristiques d'entrée
• Calcul des amplitudes de gradient pendant l'entraînement
• Mesure des distributions de poids des modèles

Ces opérations vectorielles constituent la base des architectures modernes d'apprentissage profond, où la capacité de mesurer et de manipuler des espaces à haute dimension devient essentielle pour des tâches telles que la reconnaissance d'images, le traitement du langage naturel et les systèmes autonomes. L'élégante simplicité du théorème de Pythagore continue d'alimenter certaines des applications d'intelligence artificielle les plus sophistiquées aujourd'hui.

Optimisation des algorithmes

Le théorème de Pythagore est fondamental pour les algorithmes d'optimisation, en particulier pour la descente de gradient. Lorsque nous cherchons le chemin le plus court vers une valeur minimale, nous nous appuyons souvent sur des calculs de distance basés sur ce théorème. Cette technique d'optimisation est à la base de l'apprentissage automatique moderne. Si vous souhaitez approfondir votre compréhension de ses mécanismes et de ses applications, notre tutoriel La descente de gradient dans l'apprentissage automatique propose une exploration approfondie de cette puissante technique mathématique. 

Les applications du théorème en matière d'optimisation s'étendent à divers domaines. Dans les problèmes de flux de réseau, il aide à déterminer les chemins optimaux pour la transmission des données. Lorsqu'il s'agit de minimiser des distances dans des problèmes spatiaux, le théorème guide les algorithmes pour trouver des solutions efficaces. Dans le domaine de l'apprentissage automatique, elle est particulièrement utile pour optimiser les paramètres du modèle pendant l'apprentissage, ce qui aide les algorithmes à converger vers les prédictions les plus précises possibles.

Conclusion

Le théorème de Pythagore fait le lien entre la sagesse ancestrale et l'innovation moderne. Des bâtisseurs égyptiens créant des angles droits parfaits aux scientifiques calculant des distances dans des espaces à haute dimension, cette relation mathématique ne cesse de révéler de nouvelles applications. La simple formule ^a² + ^b² = ^c² permet de comprendre des vérités géométriques complexes, depuis les mesures de base des triangles jusqu'aux algorithmes sophistiqués d'apprentissage automatique.

Si vous cherchez à passer à l'étape suivante dans l'application de ces idées, notre cours Designing Machine Learning Workflows in Python fournit un guide pratique pour intégrer des principes mathématiques comme ceux-ci dans des pipelines d'apprentissage automatique du monde réel.