Der Satz des Pythagoras: Die fundamentale Beziehung der Geometrie erforschen

Der Satz des Pythagoras ist nicht nur eine Grundvoraussetzung für die Geometrie in der Schule, sondern auch ein Eckpfeiler der linearen Algebra und bildet die Grundlage für das Verständnis von Vektornormen, Orthogonalität und Projektionen in höherdimensionalen Räumen. Diese Konzepte sind nicht nur grundlegend für die Theorie, sondern haben auch praktische Anwendungen in der Datenwissenschaft, wo sie Algorithmen des maschinellen Lernens und der Dimensionalitätsreduktion untermauern.

In diesem Artikel beginne ich am Anfang und gehe auf die Grundlagen des Satzes des Pythagoras ein. Nach und nach werde ich dann auf die fortgeschritteneren und weniger bekannten Anwendungen des Satzes in höheren Dimensionen eingehen, einschließlich seiner Rolle bei der Analyse komplexer Datensätze, der Optimierung von Machine-Learning-Modellen und der Visualisierung geometrischer Beziehungen in Data-Science-Workflows. Wenn du diese Zusammenhänge weiter erforschen und sehen willst, wie sie in der Praxis angewendet werden, bietet dir unser Kurs Lineare Algebra für Data Science in R einen praktischen Ansatz, um die Theorie mit realen Datenproblemen zu verbinden.

Einführung in den Satz des Pythagoras

Stell dir das alte Ägypten vor, wo Architekten und Baumeister vor einer großen Herausforderung standen: Sie mussten perfekte rechte Winkel für ihre großartigen Bauwerke schaffen. Ihre geniale Lösung? Ein einfaches Seil, das mit 12 gleichen Abschnitten markiert ist. Indem sie ein Dreieck mit den Seitenlängen 3, 4 und 5 bildeten, entdeckten sie, dass sie jedes Mal perfekte rechte Winkel bilden konnten.

Der Satz des Pythagoras gilt als eine der elegantesten und praktischsten Beziehungen der Mathematik. Obwohl es traditionell dem antiken griechischen Mathematiker Pythagoras (570-495 v. Chr.) zugeschrieben wird, gibt es Hinweise darauf, dass dieses fundamentale Prinzip bereits über ein Jahrtausend vor Pythagoras in mehreren antiken Zivilisationen bekannt war, darunter die Babylonier und Chinesen.

Die Formel des Satzes von Pythagoras

Der Satz des Pythagoras drückt eine klare Beziehung aus: In jedem rechtwinkligen Dreieck ist das Quadrat der Hypotenusenlänge (c) gleich der Summe der Quadrate der beiden anderen Seiten (a und b). Diese Beziehung zeigt sich in der berühmten Gleichung:

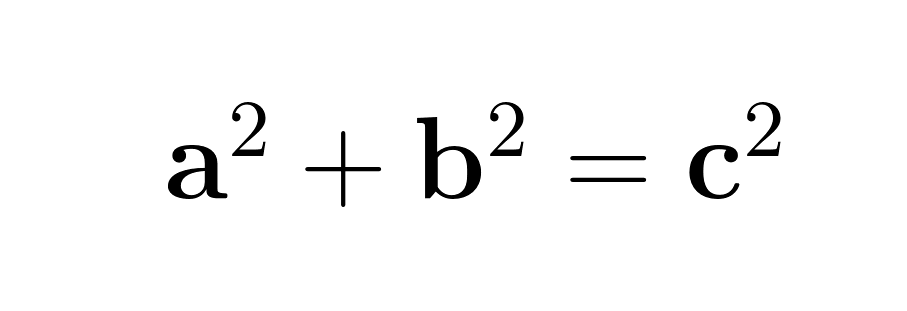
Wo:

• a und b sind die Längen der beiden Schenkel (die an den rechten Winkel angrenzenden Seiten)
• c ist die Länge der Hypotenuse (die längste Seite, die dem rechten Winkel gegenüberliegt)

Beweise für den Satz des Pythagoras

Das Verständnis der verschiedenen Beweise für den Satz des Pythagoras hilft dabei, herauszufinden, warum diese Beziehung in der gesamten Mathematik gilt. Wir wollen nun ein paar verschiedene Ansätze untersuchen, um dieses Theorem zu beweisen.

Geometrische Beweise des Satzes des Pythagoras

Im Laufe der Geschichte haben Mathematiker zahlreiche geometrische Beweise für den Satz des Pythagoras entwickelt, die jeweils einzigartige Einblicke in diese grundlegende Beziehung bieten. Lass uns einen der visuell auffälligsten Ansätze erkunden und dabei die große Vielfalt an geometrischen Demonstrationen erkennen.

Der quadratische Konstruktionsnachweis

Ein klassischer geometrischer Beweis, der in Euklids Elementenveröffentlicht wurde , ist nach wie vor eine der visuell überzeugendsten Demonstrationen des Satzes. So funktioniert es:

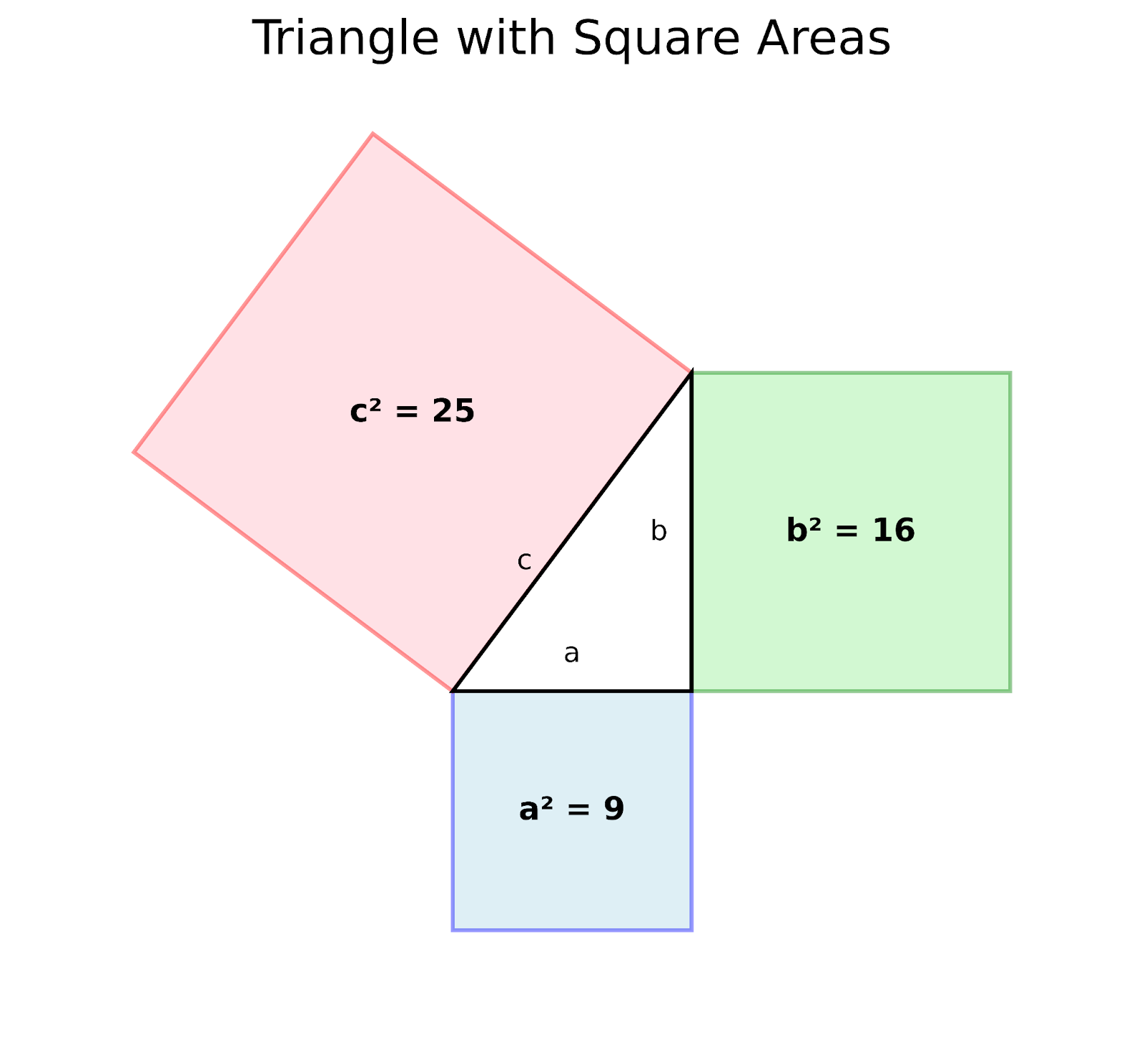
Geometrischer Beweis des Satzes von Pythagoras. Bild nach Autor

Die Konstruktion beginnt mit einem rechtwinkligen Dreieck, bei dem: 

1. Die beiden rechtwinkligen Seiten sind mit "a" und "b" (den Schenkeln) bezeichnet
2. Die längste Seite "c" ist die Hypotenuse
3. Quadrate werden entlang jeder Seite des Dreiecks gezeichnet

Die farbigen Quadrate stellen visuell dar: 

• Das blaue Quadrat hat die Fläche ^a² oder 9
• Das grüne Quadrat hat die Fläche ^b² oder 16
• Das rosa Quadrat hat die Fläche ^c² oder 25

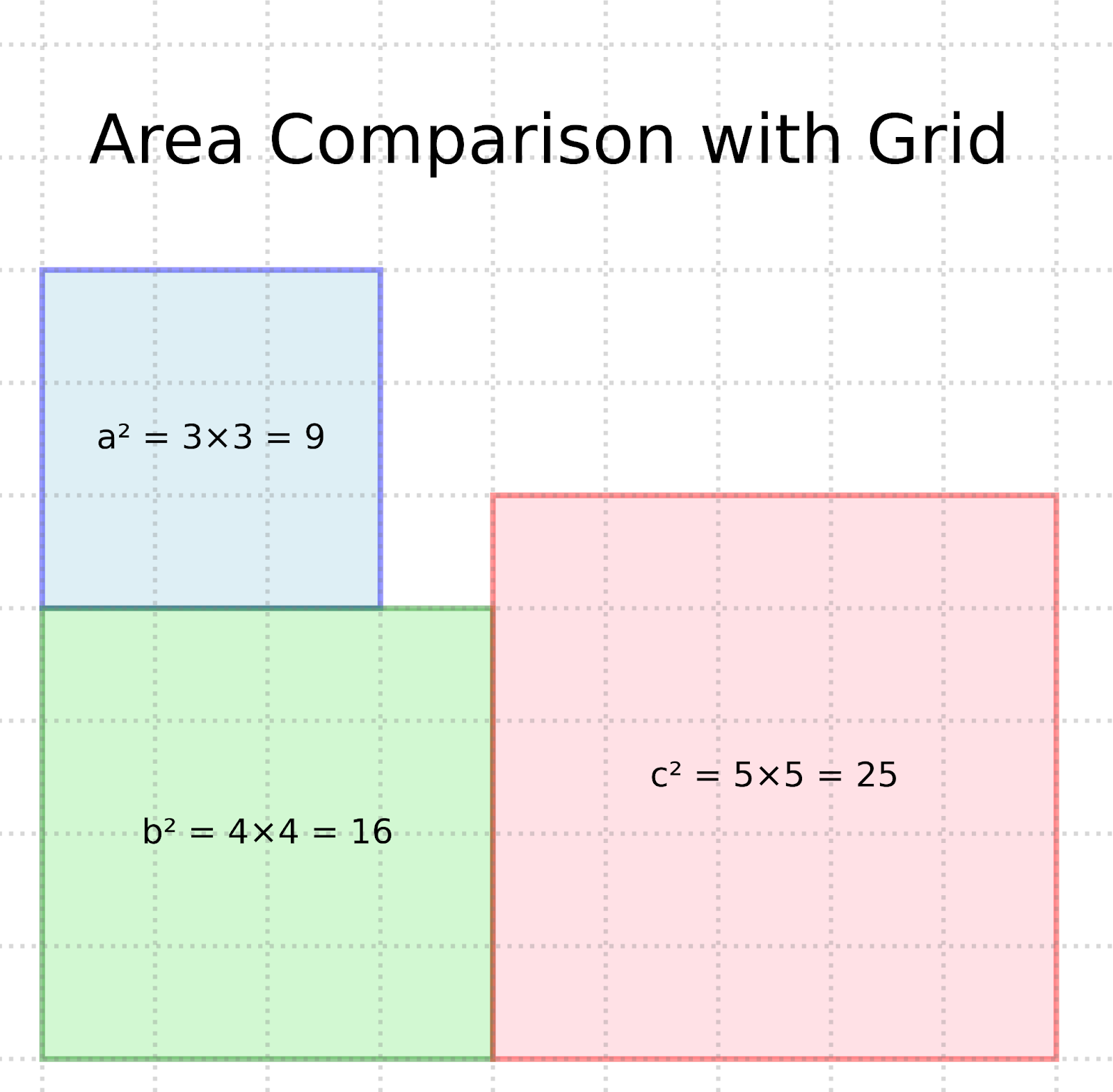
Gitternetzdarstellung des Satzes von Pythagoras. Bild nach Autor

Die Gittervisualisierung demonstriert die Gleichheit ^a² + ^b² = ^c², indem sie zeigt, dass: 

• Das blaue Quadrat misst 3×3 = 9 Quadrateinheiten (^a²) 
• Das grüne Quadrat misst 4×4 = 16 Quadrateinheiten (^b²) 
• Zusammen ergeben diese Flächen 25 Quadrateinheiten 
• Das rosa Quadrat misst 5×5 = 25 Quadrateinheiten (^c²) 

Die Brillanz dieses Beweises liegt in seiner visuellen Klarheit - du kannst buchstäblich sehen, dass die Fläche des Quadrats auf der Hypotenuse gleich der Summe der Flächen der beiden anderen Quadrate ist: 9 + 16 = 25.

Andere bemerkenswerte geometrische Ansätze

Die geometrische Wahrheit des Satzes kann mit verschiedenen anderen Methoden bewiesen werden, unter anderem:

• Halbkreisbeweis: Verwende die Beziehung zwischen den Halbkreisen, die auf jeder Seite des rechtwinkligen Dreiecks eingezeichnet sind
• Parallelogramm-Methode: Flächengleichheit mit parallelen Linien und ähnlichen Dreiecken zeigen
• Ähnlichkeitsbasierter Beweis: Verwendung der Eigenschaften ähnlicher Dreiecke, die durch die Höhe der Hypotenuse entstehen

Algebraische Beweise des Satzes des Pythagoras

In der Algebra gibt es ebenso viele verschiedene Ansätze, dieses Theorem zu beweisen. Hier ist eine elegante Demonstration, gefolgt von Verweisen auf andere wichtige algebraische Methoden.

Ansatz der ähnlichen Dreiecke

Dieser Beweis macht sich die Macht der proportionalen Beziehungen zunutze: 

1. Beginne mit einem rechtwinkligen Dreieck mit der Höhe h und der Basis b
2. Drücke die Hypotenuse c durch die Höhe und die Basis aus: ^c² = ^h² + ^b²
3. Verwende ähnliche Dreiecke, um zu zeigen, dass die entsprechenden Seiten proportional sind
4. Durch algebraische Manipulationen kommst du auf ^a² + ^b² = ^c²

Andere algebraische Demonstrationen

Das Theorem kann mit verschiedenen algebraischen Techniken überprüft werden, darunter:

• Pythagoreische Identität: Trigonometrische Beziehungen nutzen (^cos²θ+ ^sin²θ= 1)
• Quadratische Erweiterung: Erweitern perfekter Quadrate und Differenz von Quadraten
• Vektorielle Algebra: Nutzung der Eigenschaften von Punktprodukten und Vektorgrößen
• Abstandsformel Ableitung: Rückwärts arbeiten von der Abstandsformel in der Koordinatengeometrie
• Matrix-Methoden: Lineare Algebra und Transformationsmatrizen verwenden

Jede Beweismethode, ob geometrisch oder algebraisch, beleuchtet verschiedene Aspekte dieser grundlegenden Beziehung und trägt zu einem tieferen Verständnis der mathematischen Wahrheit bei. Diese verschiedenen Ansätze zeigen auch, wie sehr die verschiedenen Zweige der Mathematik miteinander verbunden sind, von der grundlegenden Geometrie bis zur fortgeschrittenen Algebra.

Andere bemerkenswerte Beweise

Der Satz des Pythagoras hat im Laufe der Geschichte Hunderte von einzigartigen Beweisen inspiriert, von denen jeder neue Erkenntnisse bietet:

1. Der Einstein-Beweis: Albert Einstein entdeckte als Teenager einen Beweis, der die Eigenschaften ähnlicher Dreiecke nutzt
2. Der Beweis für Präsident Garfield (1876): James Garfield, der 20. Präsident der USA, erstellte einen Beweis mit Hilfe eines Trapezes
3. Der Johnson-Jackson-Beweis (2023): Zwei Highschool-Schülerinnen, Calcea Johnson und Ne'Kiya Jackson von der St. Mary's Academy in New Orleans, schrieben Mathematikgeschichte, indem sie einen neuen Beweis mit Hilfe der Trigonometrie entwickelten. Ihr innovativer Ansatz löste Diskussionen über die Grundlagen mathematischer Beweise und die Beziehungen zwischen Geometrie und Trigonometrie aus. Diese Leistung zeigt, dass dieser fundamentale Satz auch nach Tausenden von Jahren noch neue mathematische Erkenntnisse liefert.

Pythagoreische Dreiergruppen und Verallgemeinerungen

Was sind pythagoreische Dreiergruppen?

Bei der Erforschung des Satzes von Pythagoras entdecken wir Mengen von drei ganzen Zahlen, die die Gleichung ^a² + ^b² = ^c² erfüllen. Diese Mengen werden pythagoräische Dreiergruppen genannt. Das bekannteste Beispiel ist (3, 4, 5), das du vielleicht aus unserer Eröffnungsgeschichte über ägyptische Baumeister kennst.

Schauen wir uns einige gängige pythagoreische Dreiergruppen an:

• (3, 4, 5): 3^² + 4^² = 9 + 16 = 25 = 5^²
• (5, 12, 13): 5^² + 12^² = 25 + 144 = 169 = 13^²
• (8, 15, 17): 8^² + 15^² = 64 + 225 = 289 = 17^²

Interessanterweise ergibt jedes pythagoreische Tripel multipliziert mit einer ganzen Zahl ein weiteres gültiges Tripel. Wenn du zum Beispiel (3, 4, 5) verdoppelst, erhältst du (6, 8, 10).

Verallgemeinerungen des Satzes von Pythagoras

Der Satz des Pythagoras geht auf faszinierende Weise über rechtwinklige Dreiecke hinaus:

1. Höhere Dimensionen: Das Konzept lässt sich auf drei Dimensionen ausdehnen, wie die Abstandsformel im 3D-Raum: ^d² = ^x² + ^y² + ^z²
2. Nicht-euklidische Geometrie: In der sphärischen Geometrie, z. B. bei der Berechnung von Entfernungen auf der Erdoberfläche, verwandelt sich das Theorem in neue Beziehungen, bei denen die Summe der Quadrate nicht immer gleich ist. Wie in der folgenden Abbildung zu sehen ist, funktioniert der Satz des Pythagoras gut auf ebenen Flächen. Für gekrümmte Flächen brauchen wir jedoch eine andere Formel, das sphärische Kosinusgesetz: cos(c) = cos(a)cos(b) + sin(a)sin(b)cos(C), wobei c die Länge der Seite und C der ihr gegenüberliegende Winkel ist.

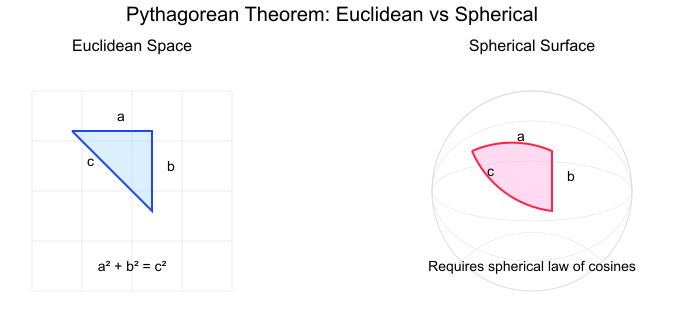
Der Satz des Pythagoras in euklidischen und nicht-euklidischen Räumen. Bild vom Autor

3. Das Kosinusgesetz: Diese Verallgemeinerung gilt für jedes Dreieck, nicht nur für rechtwinklige Dreiecke: ^c² = ^a² + ^b² - 2ab cos(C) Wenn der Winkel C 90° beträgt, ist cos(C) = 0 und wir erhalten wieder unseren bekannten Satz des Pythagoras.

Diese Verallgemeinerungen zeigen, wie eine einfache Beziehung zwischen den Seiten eines rechtwinkligen Dreiecks die Türen zum Verständnis von Raum, Entfernung und Geometrie in breiteren Kontexten öffnet.

Der Satz des Pythagoras in der Programmierung und Datenwissenschaft

Distanzmaße beim maschinellen Lernen

Der Satz des Pythagoras bildet die Grundlage für den euklidischen Abstand, eine weit verbreitete Metrik beim maschinellen Lernen. Wenn ein Algorithmus bestimmen muss, wie ähnlich oder unterschiedlich zwei Datenpunkte sind, nutzt er oft dieses Prinzip. Wir werden uns hier mit einer grundlegenden Implementierung befassen. Eine vollständige Untersuchung der Distanzmetriken und ihrer Anwendungen findest du auf Euklidische Distanz verstehen: Von der Theorie zur Praxis besonders wertvoll.

Nimm ein einfaches Beispiel: Vergleiche Häuser anhand ihrer Größe (x-Achse) und ihres Preises (y-Achse). Der euklidische Abstand zwischen zwei Häusern in diesem Merkmalsraum sagt uns, wie ähnlich sie sich sind:

import numpy as np

def euclidean_distance(point1, point2):
    return np.sqrt(np.sum((point1 - point2) ** 2))

# Example: Two houses
house1 = np.array([1500, 300000])  # 1500 sq ft, $300,000
house2 = np.array([2000, 450000])  # 2000 sq ft, $450,000
distance = euclidean_distance(house1, house2)

Diese Abstandsmetrik ist besonders leistungsfähig in Empfehlungssystemen und Clustering-Algorithmen, wo sie dabei hilft, Muster zu erkennen und ähnliche Objekte zusammenzufassen. Netflix nutzt zum Beispiel ähnliche Abstandsberechnungen, um Filme auf der Grundlage des Sehverhaltens vorzuschlagen, und E-Commerce-Plattformen verwenden sie, um Produkte auf der Grundlage der Vorlieben der Nutzer/innen zu empfehlen.

Anwendungen in der linearen Algebra

Das Theorem hilft uns, Vektoroperationen zu verstehen, insbesondere bei der Berechnung von Vektorgrößen und der Bestimmung der Orthogonalität:

def vector_magnitude(vector):
    """Calculate the length (magnitude) of a vector"""
    return np.sqrt(np.sum(vector ** 2))

# Example: 3D vector
vector = np.array([3, 4, 5])
magnitude = vector_magnitude(vector)

Dieses Konzept lässt sich auf neuronale Netze übertragen, bei denen die Berechnung von Vektorgrößen hilft:

• Normalisierung der Eingangsmerkmale
• Berechnung der Gradientengrößen während des Trainings
• Messung von Modellgewichtsverteilungen

Diese Vektoroperationen bilden die Grundlage für moderne Deep-Learning-Architekturen, bei denen die Fähigkeit, hochdimensionale Räume zu messen und zu manipulieren, für Aufgaben wie Bilderkennung, Verarbeitung natürlicher Sprache und autonome Systeme von zentraler Bedeutung ist. Die elegante Einfachheit des Satzes des Pythagoras ist auch heute noch die Grundlage für einige der anspruchsvollsten KI-Anwendungen.

Optimierung in Algorithmen

Der Satz des Pythagoras ist grundlegend für Optimierungsalgorithmen, insbesondere für den Gradientenabstieg. Bei der Suche nach dem kürzesten Weg zu einem Mindestwert verlassen wir uns häufig auf Entfernungsberechnungen, die auf diesem Theorem basieren. Diese Optimierungstechnik ist die Grundlage für modernes maschinelles Lernen. Wenn du dein Verständnis der Mechanismen und Anwendungen vertiefen möchtest, bietet dir unser Tutorial Gradientenabstieg im maschinellen Lernen einen umfassenden Einblick in diese leistungsstarke mathematische Technik. 

Das Theorem lässt sich in verschiedenen Bereichen zur Optimierung einsetzen. Bei Netzwerkflussproblemen hilft sie dabei, optimale Pfade für die Datenübertragung zu bestimmen. Bei der Minimierung von Distanzen in räumlichen Problemen leitet das Theorem Algorithmen an, um effiziente Lösungen zu finden. Beim maschinellen Lernen ist sie besonders wertvoll, um die Modellparameter während des Trainings zu optimieren und den Algorithmen zu helfen, möglichst genaue Vorhersagen zu treffen.

Fazit

Der Satz des Pythagoras verbindet alte Weisheit mit moderner Innovation. Von ägyptischen Baumeistern, die perfekte rechte Winkel erschaffen, bis hin zu Datenwissenschaftlern, die Entfernungen in hochdimensionalen Räumen berechnen, offenbart diese mathematische Beziehung immer wieder neue Anwendungen. Die einfache Formel ^a² + ^b² = ^c² öffnet Türen zum Verständnis komplexer geometrischer Wahrheiten, die von einfachen Dreiecksmessungen bis hin zu ausgeklügelten Algorithmen für maschinelles Lernen reichen.

Wenn du den nächsten Schritt bei der Anwendung dieser Ideen machen möchtest, bietet dir unser Kurs Designing Machine Learning Workflows in Python einen praktischen Leitfaden, um mathematische Prinzipien wie diese in reale Machine Learning Pipelines zu integrieren.