Pythagorean Theorem: Exploring Geometry's Fundamental Relation

The Pythagorean theorem is more than just a staple of high school geometry; it’s a cornerstone of linear algebra, forming the basis for understanding vector norms, orthogonality, and projections in higher-dimensional spaces. These concepts are not only fundamental to the theory but also have practical applications in data science, where they underpin algorithms in machine learning and dimensionality reduction.

In this article, I will start at the beginning and review the basics of the Pythagorean theorem, and slowly I will build towards the more advanced and lesser-known applications of the theorem in higher dimensions, including its role in analyzing complex datasets, optimizing machine learning models, and visualizing geometric relationships in data science workflows. If you're looking to explore these connections further and see how they apply in practice, our Linear Algebra for Data Science in R course offers a hands-on approach to bridging theory and real-world data problems.

Introduction to the Pythagorean Theorem

Picture ancient Egypt, where architects and builders faced a compelling challenge: creating perfect right angles for their magnificent structures. Their ingenious solution? A simple rope marked with 12 equal sections. By forming a triangle with sides of 3, 4, and 5 units, they discovered they could create perfect right angles every time.

The Pythagorean theorem stands as one of mathematics' most elegant and practical relationships. While traditionally credited to the ancient Greek mathematician Pythagoras (570-495 BCE), evidence suggests this fundamental principle was known to several ancient civilizations, including the Babylonians and Chinese, over a millennium before Pythagoras systematically proved it.

The Pythagorean Theorem Formula

The Pythagorean theorem expresses a clear relationship: in any right triangle, the square of the hypotenuse length (c) equals the sum of squares of the other two sides (a and b). This relationship appears in the famous equation:

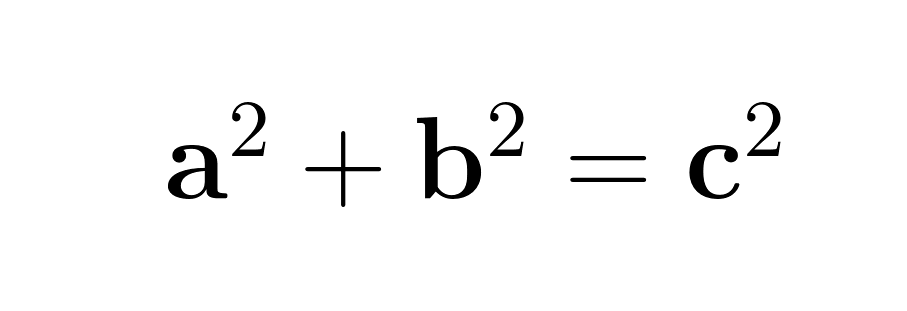
Where:

• a and b are the lengths of the two legs (the sides adjacent to the right angle)
• c is the length of the hypotenuse (the longest side, opposite the right angle)

Pythagorean Theorem Proofs

Understanding different proofs of the Pythagorean theorem helps reveal why this relationship holds true across mathematics. Let's explore a few distinct approaches to proving this theorem.

Geometric proofs of the Pythagorean theorem

Throughout history, mathematicians have developed numerous geometric proofs of the Pythagorean theorem, each offering unique insights into this fundamental relationship. Let's explore one of the most visually striking approaches, while acknowledging the rich variety of geometric demonstrations available.

The square construction proof

One classic geometric proof, popularized in Euclid's Elements, remains one of the most visually compelling demonstrations of the theorem. Here's how it works:

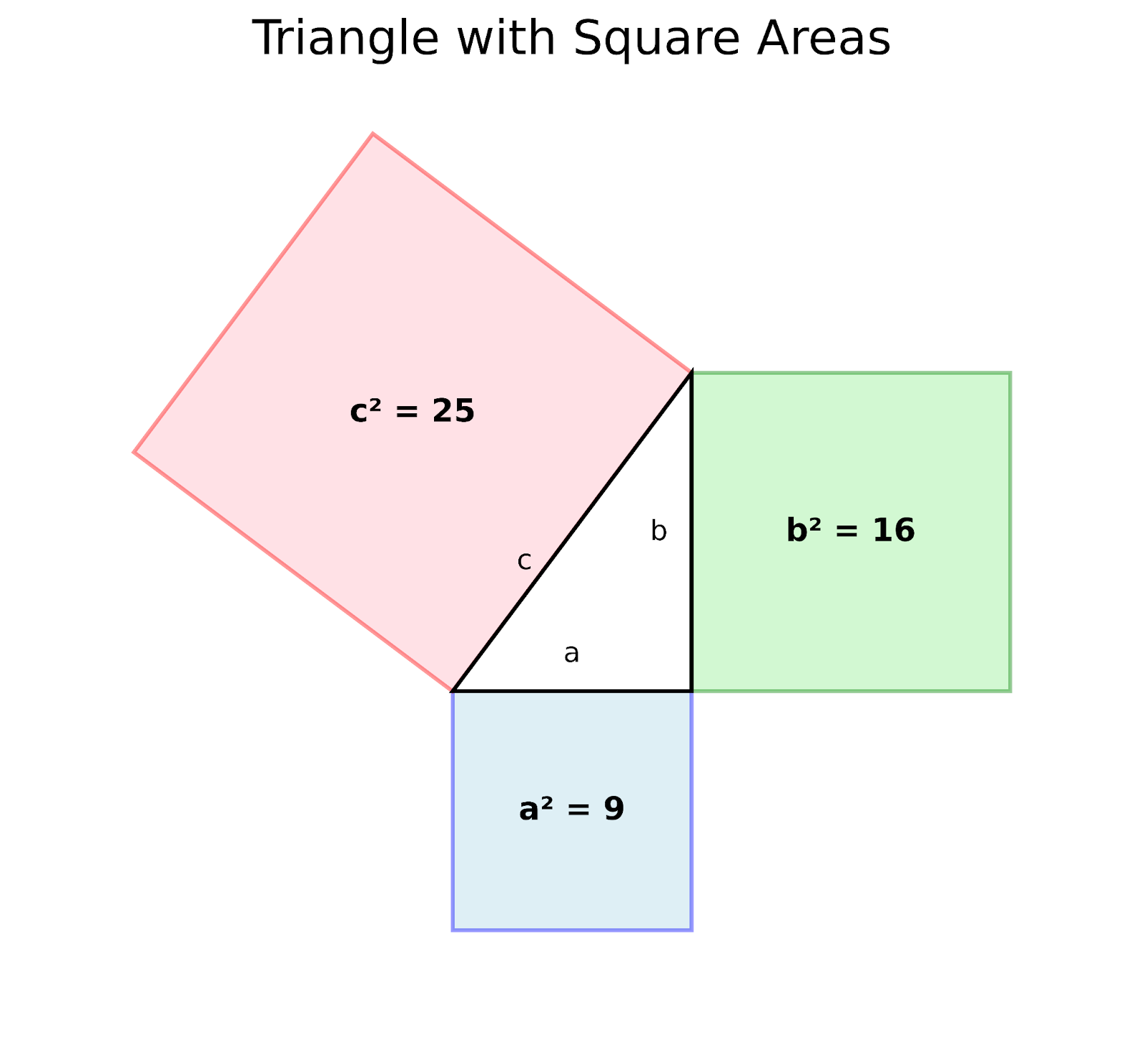
Geometric proof of the Pythagorean theorem. Image By Author

The construction starts with a right triangle where: 

1. The two perpendicular sides are labeled 'a' and 'b' (the legs)
2. The longest side 'c' is the hypotenuse
3. Squares are drawn along each side of the triangle

The colored squares visually represent: 

• The blue square has area a^² or 9
• The green square has area b^² or 16
• The pink square has area c^² or 25

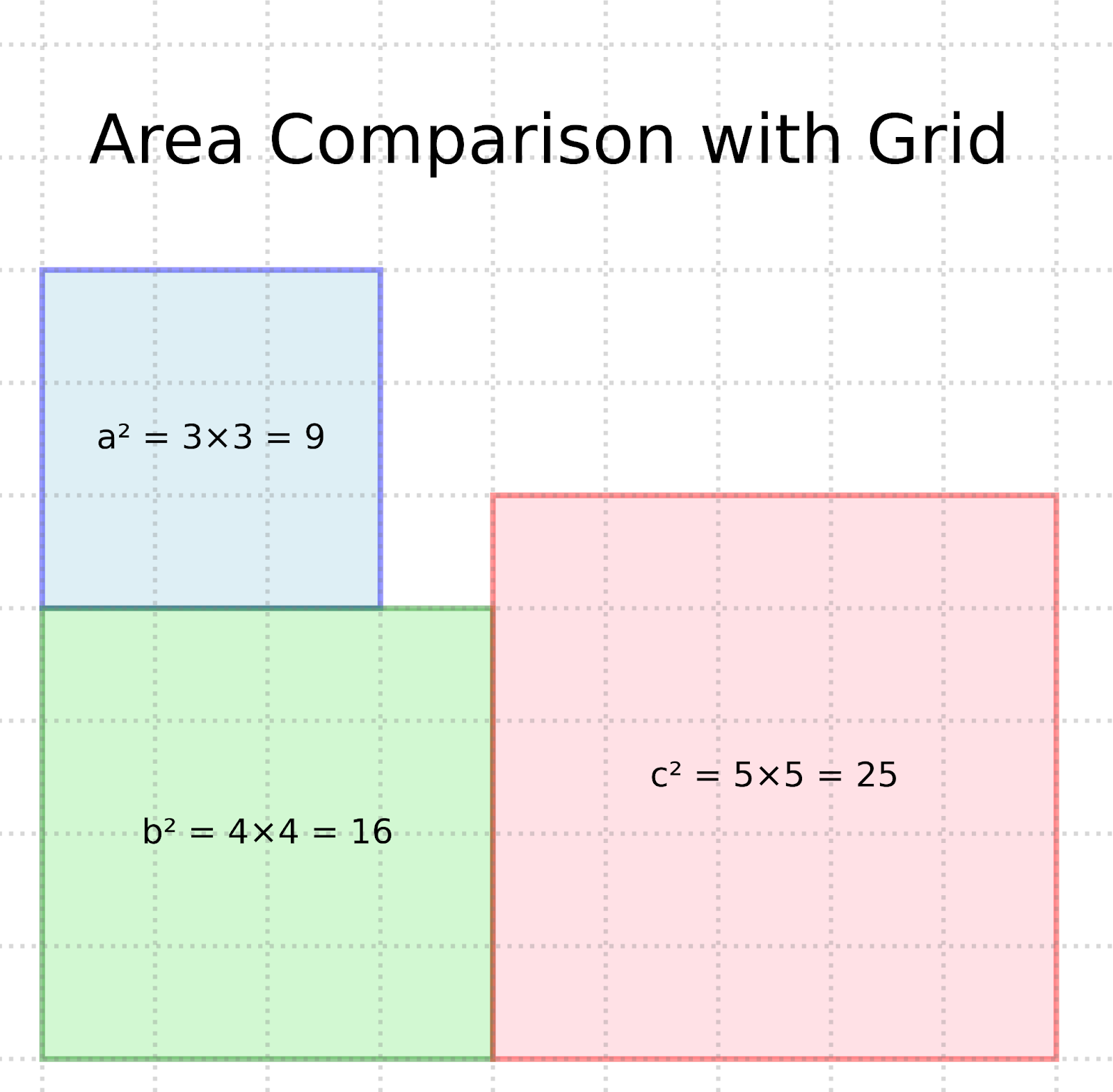
Grid representation of the Pythagorean theorem. Image By Author

The grid visualization demonstrates the equality a^² + b^² = c^² by showing that: 

• The blue square measures 3×3 = 9 square units (a^²) 
• The green square measures 4×4 = 16 square units (b^²) 
• Together, these areas sum to 25 square units 
• The pink square measures 5×5 = 25 square units (c^²) 

The brilliance of this proof lies in its visual clarity - you can literally see that the area of the square on the hypotenuse equals the sum of the areas of the other two squares: 9 + 16 = 25.

Other notable geometric approaches

The theorem's geometric truth can be demonstrated through various other methods, including:

• Semicircle Proof: Using the relationship between semicircles drawn on each side of the right triangle
• Parallelogram Method: Showing area equivalence using parallel lines and similar triangles
• Similarity-Based Proof: Using the properties of similar triangles created by the altitude to the hypotenuse

Algebraic proofs of the Pythagorean theorem

The algebraic realm offers equally diverse approaches to proving this theorem. Here's one elegant demonstration, followed by references to other significant algebraic methods.

Similar triangles approach

This proof leverages the power of proportional relationships: 

1. Begin with a right triangle with height h and base b
2. Express the hypotenuse c using the height and base: c^² = h^² + b^²
3. Use similar triangles to show that corresponding sides are proportional
4. Through algebraic manipulation, arrive at a^² + b^² = c^²

Other algebraic demonstrations

The theorem can be verified through various algebraic techniques, including:

• Pythagorean Identity: Using trigonometric relationships (cos^²θ + sin^²θ = 1)
• Quadratic Expansion: Expanding perfect squares and difference of squares
• Vector Algebra: Utilizing dot product properties and vector magnitudes
• Distance Formula Derivation: Working backwards from the distance formula in coordinate geometry
• Matrix Methods: Using linear algebra and transformation matrices

Each proof method, whether geometric or algebraic, illuminates different aspects of this fundamental relationship, contributing to our deeper understanding of mathematical truth. These various approaches also demonstrate the interconnected nature of different branches of mathematics, from basic geometry to advanced algebra.

Other notable proofs

The Pythagorean theorem has inspired hundreds of unique proofs throughout history, each offering fresh insights:

1. Einstein's Proof: A teenage Albert Einstein discovered a proof using the properties of similar triangles
2. President Garfield's Proof (1876): James Garfield, the 20th U.S. president, created a proof using a trapezoid
3. The Johnson-Jackson Proof (2023): Two high school seniors, Calcea Johnson and Ne'Kiya Jackson from St. Mary's Academy in New Orleans, made mathematical history by developing a new proof using trigonometry. Their innovative approach sparked discussions about the foundations of mathematical proofs and the relationships between geometry and trigonometry. The achievement demonstrates that even after thousands of years, this fundamental theorem continues to yield new mathematical insights.

Pythagorean Triples and Generalizations

What are Pythagorean triples?

When exploring the Pythagorean theorem, we discover sets of three whole numbers that satisfy the equation a^² + b^² = c^². These sets are called Pythagorean triples. The most familiar example is (3, 4, 5), which you might recognize from our opening story about Egyptian builders.

Let's look at some common Pythagorean triples:

• (3, 4, 5): 3^² + 4^² = 9 + 16 = 25 = 5^²
• (5, 12, 13): 5^² + 12^² = 25 + 144 = 169 = 13^²
• (8, 15, 17): 8^² + 15^² = 64 + 225 = 289 = 17^²

Interestingly, any Pythagorean triple multiplied by a whole number creates another valid triple. For example, doubling (3, 4, 5) gives us (6, 8, 10).

Generalizations of the Pythagorean theorem

The Pythagorean theorem extends beyond right triangles in fascinating ways:

1. Higher Dimensions: The concept expands into three dimensions as the distance formula in 3D space: d^² = x^² + y^² + z^²
2. Non-Euclidean Geometry: In spherical geometry, like calculating distances on Earth's surface, the theorem transforms into new relationships where the sum of the squares isn't always equal. As shown in the illustration below, the Pythagorean theorem works well on flat surfaces. But, when we move to curved surfaces, we need a different formula called the spherical law of cosines: cos(c) = cos(a)cos(b) + sin(a)sin(b)cos(C), where c is the length of the side and C is the angle opposite to it.

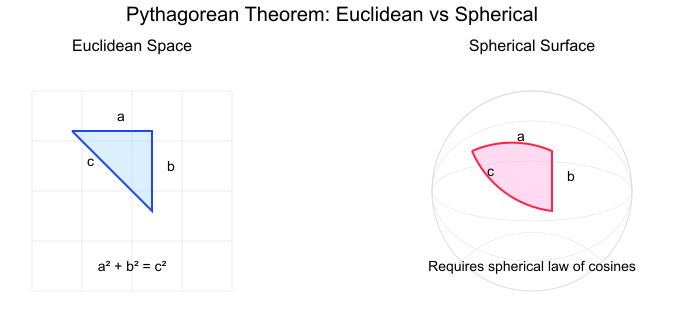
Pythagorean theorem in Euclidean and non-Euclidean spaces. Image by Author

3. The Law of Cosines: This generalization works for any triangle, not just right triangles: c^² = a^² + b^² - 2ab cos(C) When the angle C is 90°, cos(C) = 0, and we get back our familiar Pythagorean theorem.

These generalizations reveal how a simple relationship between the sides of a right triangle opens doors to understanding space, distance, and geometry in broader contexts.

The Pythagorean Theorem in Programming and Data Science

Distance measures in machine learning

The Pythagorean theorem forms the basis of Euclidean distance, a widely used metric in machine learning. When an algorithm needs to determine how similar or different two data points are, it often uses this principle. We'll explore a basic implementation here, and for a complete exploration of distance metrics and their applications, you'll find our Understanding Euclidean Distance: From Theory to Practice particularly valuable.

Consider a simple example: comparing houses based on their size (x-axis) and price (y-axis). The Euclidean distance between two houses in this feature space tells us how similar they are:

import numpy as np

def euclidean_distance(point1, point2):
    return np.sqrt(np.sum((point1 - point2) ** 2))

# Example: Two houses
house1 = np.array([1500, 300000])  # 1500 sq ft, $300,000
house2 = np.array([2000, 450000])  # 2000 sq ft, $450,000
distance = euclidean_distance(house1, house2)

This distance metric becomes particularly powerful in recommendation systems and clustering algorithms, where it helps identify patterns and group similar items together. For instance, Netflix uses similar distance calculations to suggest movies based on viewing patterns, and e-commerce platforms employ them to recommend products based on user preferences.

Applications in linear algebra

The theorem helps us understand vector operations, particularly in calculating vector magnitudes and determining orthogonality:

def vector_magnitude(vector):
    """Calculate the length (magnitude) of a vector"""
    return np.sqrt(np.sum(vector ** 2))

# Example: 3D vector
vector = np.array([3, 4, 5])
magnitude = vector_magnitude(vector)

This concept extends to neural networks, where calculating vector magnitudes helps in:

• Normalizing input features
• Computing gradient magnitudes during training
• Measuring model weight distributions

These vector operations form the foundation of modern deep learning architectures, where the ability to measure and manipulate high-dimensional spaces becomes central for tasks like image recognition, natural language processing, and autonomous systems. The elegant simplicity of the Pythagorean theorem continues to power some of the most sophisticated AI applications today.

Optimization in algorithms

The Pythagorean theorem is fundamental to optimization algorithms, especially in gradient descent. When seeking the shortest route to a minimum value, we frequently rely on distance calculations informed by this theorem. This optimization technique drives modern machine learning. If you're eager to deepen your understanding of its mechanics and applications, our tutorial Gradient Descent in Machine Learning provides an extensive exploration of this powerful mathematical technique. 

The theorem's optimization applications extend across various domains. In network flow problems, it helps determine optimal paths for data transmission. When minimizing distances in spatial problems, the theorem guides algorithms to find efficient solutions. In machine learning, it's particularly valuable for optimizing model parameters during training, helping algorithms converge on the most accurate predictions possible.

Conclusion

The Pythagorean theorem bridges ancient wisdom with modern innovation. From Egyptian builders creating perfect right angles to data scientists calculating distances in high-dimensional spaces, this mathematical relationship continues to reveal new applications. The simple formula a^² + b^² = c^² opens doors to understanding complex geometric truths, leading from basic triangle measurements to sophisticated machine learning algorithms.

If you are looking to take the next step in applying these ideas, our Designing Machine Learning Workflows in Python course provides a practical guide to integrating mathematical principles like these into real-world machine learning pipelines.