Curso
Este tutorial sobre bucles en R analizará las construcciones disponibles en R para la creación de bucles, cuándo deben utilizarse las construcciones y cómo hacer uso de alternativas, como la función de vectorización de R, para realizar sus tareas de bucle de forma más eficiente.
El post presentará algunos ejemplos de bucles para luego criticarlos y desaprobarlos en favor de las alternativas vectorizadas más populares entre las muchas que están disponibles en el rico conjunto de librerías que ofrece R.
En general, el consejo de este tutorial de R sobre bucles sería: aprenda sobre bucles. Le ofrecen una visión detallada de lo que se supone que ocurre a nivel elemental, así como le proporcionan una comprensión de los datos que está manipulando.
Y después de haber comprendido bien los bucles, deshazte de ellos.
Esfuérzate en conocer las alternativas vectorizadas. Merece la pena en términos de eficiencia.
Para practicar de forma interactiva, pruebe el capítulo sobre bucles de nuestro curso intermedio de R.
¿Qué son los bucles?
"Hacer bucles", "hacer ciclos", "iterar" o simplemente replicar instrucciones es una práctica antigua que se originó mucho antes de la invención de los ordenadores. No es más que automatizar un proceso de varios pasos organizando secuencias de acciones o procesos "por lotes" y agrupando las partes que deben repetirse.
Todos los lenguajes de programación modernos ofrecen construcciones especiales que permiten la repetición de instrucciones o bloques de instrucciones.
En términos generales, existen dos tipos de estas construcciones especiales o bucles en los lenguajes de programación modernos. Algunos bucles se ejecutan un número determinado de veces, controlado por un contador o un índice que se incrementa en cada ciclo de iteración. Forman parte de la familia de bucles for.
Por otra parte, algunos bucles se basan en la aparición y verificación de una condición lógica. La condición se comprueba al principio o al final de la construcción del bucle. Estas variantes pertenecen a la familia de bucles while o repeat, respectivamente.
Introducción a los bucles en R
Según el manual base de R, entre los comandos de flujo de control, las construcciones de bucle son for, while y repeat, con las cláusulas adicionales break y next.
Recuerde que los comandos de flujo de control son los comandos que permiten a un programa bifurcarse entre alternativas, o "tomar decisiones", por así decirlo.
Siempre puede ver estos comandos de flujo de control invocando ?Control en la línea de comandos de RStudio.
?ControlEste diagrama de flujo muestra las estructuras del bucle R:
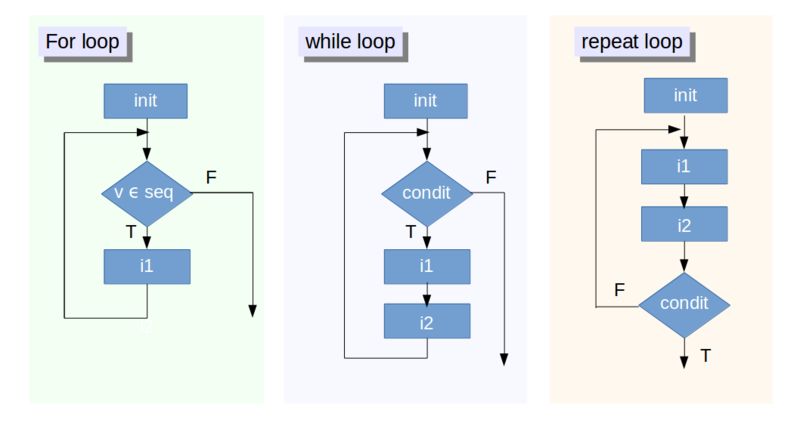
Bucles For en R
En las próximas secciones se analizará más detenidamente cada una de estas estructuras que se muestran en la figura anterior. Empezaremos nuestra discusión con la estructura de la izquierda, y continuaremos las siguientes secciones pasando gradualmente a las estructuras de la derecha.
Para una introducción en vídeo a los bucles for y un ejercicio de seguimiento, pruebe el capítulo sobre bucles for de nuestro curso intermedio de R.
Explicación de los bucles For
Esta estructura de bucle, compuesta por la caja rectangular 'init' (o inicialización), la decisión diamante o rombo, y la caja rectangular i1 se ejecuta un número conocido de veces.
En términos de diagrama de flujo, las casillas rectangulares significan algo así como "hacer algo que no implica decisiones". Los rombos o diamantes, en cambio, se denominan "símbolos de decisión" y, por tanto, se traducen en preguntas que sólo tienen dos respuestas lógicas posibles, a saber, Verdadero (V) o Falso (F).
Obsérvese que, para simplificar, se han omitido en la figura otros posibles símbolos.
Una o más instrucciones dentro del rectángulo de inicialización son seguidas por la evaluación de la condición sobre una variable que puede asumir valores dentro de una secuencia especificada. En la figura, esto se representa mediante el rombo: los símbolos significan "¿pertenece el valor actual de la variable va la secuencia seq?".
En otras palabras, está comprobando si el valor actual de vse encuentra dentro de un rango especificado. Normalmente se define este rango en la inicialización, con algo como 1:100 para asegurar que el bucle se inicia.
Si la condición no se cumple y el resultado es False, el bucle nunca se ejecuta. Así lo indica la flecha suelta a la derecha de la estructura del bucle for. El programa ejecutará entonces la primera instrucción encontrada después del bloque de bucle.
Si se verifica la condición, se ejecuta una instrucción -o bloque de instrucciones- i1. Y quizás este bloque de instrucciones sea otro bucle. En estos casos, se habla de bucle anidado.
Una vez hecho esto, se vuelve a evaluar la condición. Así lo indican las líneas que van de i1 hacia arriba, inmediatamente después del cuadro de inicialización. En R -y en Python- es posible expresarlo en lenguaje llano, preguntando si nuestra variable pertenece o no a un rango de valores.
Observe que en otros lenguajes, por ejemplo en C, la condición se hace más explícita con el uso de un operador lógico, como mayor o menor que, igual a, ....
He aquí un ejemplo de un simple bucle for:
# Create a vector filled with random normal values
u1 <- rnorm(30)
print("This loop calculates the square of the first 10 elements of vector u1")
# Initialize `usq`
usq <- 0.
for (i in 1:10) {
# i-th element of `u1` squared into `i`-th position of `usq`
usq[i] <- u1[i] * u1[i]
print(usq[i])
}
print(i)El bloque for está contenido entre llaves. Pueden colocarse inmediatamente después de la condición de prueba o debajo de ella, preferiblemente seguidas de una hendidura. Nada de esto es obligatorio, pero las llaves definitivamente mejoran la legibilidad de su código y permiten detectar fácilmente el bloque de bucle y los errores potenciales dentro de él.
Nótese que el vector de los cuadrados, usq, está inicializado. Esto no sería necesario en el código plano de RStudio, pero en la versión de marcado, knitr no compilaría porque no se encuentra una referencia al vector antes de su uso en el bucle, lanzando así un error dentro de RStudio. Para más información sobre knitr, vaya a la página de R Markdown.
Anidamiento de bucles
Ahora que sabes que los bucles for también se pueden anidar, probablemente te estés preguntando por qué y cuándo usarías esto en tu código.
Bien, supongamos que desea manipular una matriz bidimensional estableciendo sus elementos en valores específicos.
Entonces podrías hacer algo así:
# Insert your own integer here
my_int <- 42
nr <- as.integer(my_int)
# Create a `n` x `n` matrix with zeros
mymat <- matrix(0, nr, nr)
# For each row and for each column, assign values based on position
# These values are the product of two indexes
for (i in 1:dim(mymat)[1]) {
for (j in 1:dim(mymat)[2]) {
mymat[i, j] = i * j
}
}Consejo: para más información sobre la función matrix(), visite Documentación de R.
i recorre las líneas y j recorre las columnas.Bueno, has hecho la tabla de multiplicar que ya conoces de memoria.
También puede elegir un número entero y luego producir una tabla según su elección: puede asignar un número entero a una variable si la tabla es cuadrada o a dos variables si la tabla es rectangular. Esta variable servirá entonces de límite superior a los índices i y j.
# Show the first 10x10 chunk or the first `nr` x `nr` chunk
if (nr > 10) {
mymat[1:10, 1:10]
} else
mymat[1:nr, 1:nr]Observe que para evitar que el usuario sature la pantalla con tablas enormes, se pone una condición al final para imprimir el primer trozo de 10 x 10, sólo si el usuario pide un número entero mayor que 10. Si no, se imprimirá un trozo de n x n.
El código completo tiene este aspecto:
# Insert your own integer here
my_int <- 42
nr <- as.integer(my_int)
# Create a `n` x `n` matrix with zeroes
mymat <- matrix(0, nr, nr)
# For each row and for each column, assign values based on position
# These values are the product of two indexes
for (i in 1:dim(mymat)[1]) {
for (j in 1:dim(mymat)[2]) {
mymat[i, j] = i * j
}
}
# Show the first 10x10 chunk or the first `nr` x `nr` chunk
if (nr > 10) {
mymat[1:10, 1:10]
} else
mymat[1:nr, 1:nr]Para bucles: Popular pero no siempre perfecto para su uso
El bucle for es, con mucho, el más popular, y su construcción implica que el número de iteraciones es fijo y conocido de antemano, como en casos como "generar los 200 primeros números primos" o "alistar a los 10 clientes más importantes".
Pero, ¿qué ocurre si no se conoce o no se controla el número de iteraciones, y pueden darse una o varias condiciones no predecibles de antemano?
Por ejemplo, puede querer contar el número de clientes que viven en una zona identificada por un código postal determinado, o el número de clics en el banner de una página web en los dos últimos días, o imprevistos similares.
En casos así, el bucle while y su primo repeat pueden venir al rescate...
Bucles While
El bucle while, situado en el centro de la figura anterior, se compone de un bloque de inicialización como antes, seguido de una condición lógica. Esta condición se expresa típicamente mediante la comparación entre una variable de control y un valor, utilizando mayor que, menor que o igual a, pero cualquier expresión que evalúe a un valor lógico, Verdadero o Falso, es legítima.
Si el resultado es Falso (F), el bucle nunca se ejecuta, como indica la flecha suelta de la derecha de la figura. El programa ejecutará entonces la primera instrucción que encuentre después del bloque de bucle.
Si es Verdadero (T), se ejecuta a continuación la instrucción o bloque de instrucciones i1.
Observe que se ha añadido una instrucción adicional o bloque de instrucciones i2: esto sirve como actualización para la variable de control, que puede alterar el resultado de la condición al inicio del bucle, pero no es necesario. O tal vez quieras añadir un incremento a un contador para llevar la cuenta del número de iteraciones ejecutadas. Las iteraciones cesan una vez que la condición se evalúa como falsa.
El formato es while(cond) expr, donde cond es la condición a comprobar y expr es una expresión.
Por ejemplo, el siguiente bucle pide al usuario con una Función Definida por el Usuario o UDF que introduzca la respuesta correcta a la pregunta universo y todo. A continuación, seguirá haciéndolo hasta que el usuario acierte la respuesta:
# Your User Defined Function
readinteger <- function(){
n <- readline(prompt="Please, enter your ANSWER: ")
}
response <- as.integer(readinteger())
while (response!=42) {
print("Sorry, the answer to whatever the question MUST be 42");
response <- as.integer(readinteger());
}Para empezar, utilice una función definida por el usuario para obtener la entrada del usuario antes de entrar en el bucle. Este bucle continuará mientras la respuesta no sea la esperada 42.
En otras palabras, usted hace esto porque de lo contrario, R se quejaría de la expresión faltante que se suponía debía proporcionar el True o False requerido - y de hecho, no conoce 'respuesta' antes de usarla en el bucle. También lo hace porque, si responde bien a la primera, el bucle no se ejecutará en absoluto.
Repetir bucles
El bucle repeat se encuentra en el extremo derecho del diagrama de flujo que encontrará más arriba. Este bucle es similar al bucle while, pero está hecho de forma que los bloques de instrucciones i1 y i2 se ejecutan al menos una vez, sin importar el resultado de la condición.
Adhiriéndose a otros lenguajes, se podría llamar a este bucle "repetir hasta" para enfatizar el hecho de que las instrucciones i1 y i2 se ejecutan hasta que la condición sigue siendo Falsa (F) o, equivalentemente, se convierte en Verdadera (T), saliendo así; pero en cualquier caso, al menos una vez.
Como variación del ejemplo anterior, puede escribir:
readinteger <- function(){
n <- readline(prompt="Please, enter your ANSWER: ")
}
repeat {
response <- as.integer(readinteger());
if (response == 42) {
print("Well done!");
break
} else print("Sorry, the answer to whatever the question MUST be 42");
}Después de la ya conocida función de entrada, tenemos el bucle repeat cuyo bloque se ejecuta al menos una vez y que terminará siempre que se verifique la condición if.
Tenga en cuenta que tuvo que establecer una condición dentro del bucle para salir con la cláusula break. Esta cláusula nos introduce en la noción de salida o interrupción de ciclos dentro de bucles.
Interrupción y bucles de salida en R
¿Cómo se sale de un bucle?
En otros términos, aparte del final "natural" del bucle, que se produce porque se ha alcanzado el número de iteraciones prescrito (for) o porque se ha cumplido una condición (while, repeat), ¿se puede detener o interrumpir el bucle?
Y en caso afirmativo, ¿cómo?
La declaración break responde a la primera pregunta: ya lo ha visto en el último ejemplo.
Rompa sus bucles con break
Cuando el intérprete de R encuentra una interrupción, pasará el control a la instrucción inmediatamente posterior al final del bucle (si existe). En el caso de bucles anidados, la break permitirá salir sólo del bucle más interno.
He aquí un ejemplo.
Este trozo de código define una matriz de ceros m x n y luego entra en un bucle anidado for para rellenar las posiciones de la matriz, pero sólo si los dos índices difieren. El objetivo es crear una matriz triangular inferior, es decir, una matriz cuyos elementos por debajo de la diagonal principal sean distintos de cero. Los demás se dejan intactos a su valor cero inicializado.
Cuando los índices son iguales y por tanto se cumple la condición del bucle interior, que recorre el índice de la columna j, se ejecuta un break y se interrumpe el bucle interior con un salto directo a la instrucción siguiente al bucle interior. Esta instrucción es una instrucción print(). A continuación, el control llega a la condición for externa (sobre las filas, índice i), que se evalúa de nuevo.
Si los índices difieren, se realiza la asignación y el contador se incrementa en 1. Al final, el programa imprime el contador ctr, que contiene el número de elementos que se asignaron.
# Make a lower triangular matrix (zeroes in upper right corner)
m = 10
n = 10
# A counter to count the assignment
ctr = 0
# Create a 10 x 10 matrix with zeroes
mymat = matrix(0, m, n)
for (i in 1:m) {
for (j in 1:n) {
if (i == j) {
break
} else {
# you assign the values only when i<>j
mymat[i, j] = i * j
ctr = ctr + 1
}
}
print(i * j)
}
# Print how many matrix cells were assigned
print(ctr)Tenga en cuenta que puede ser un poco cauteloso poner llaves incluso cuando no son estrictamente necesarias. Suele hacerlo para asegurarse de que todo lo que se abre con {, también se cierra con }. Por lo tanto, si observa que no coinciden los números de { o }, sabrá que hay un error, aunque lo contrario no es necesariamente cierto.
El uso de next en los bucles
next interrumpe una iteración determinada y salta al ciclo siguiente. De hecho, salta a la evaluación de la condición que sostiene el bucle actual.
En otros lenguajes, puedes encontrar el equivalente (ligeramente confuso) llamado "continuar", que significa lo mismo: estés donde estés, al verificarse la condición, salta a la evaluación del bucle.
Un ejemplo más sencillo de mantener el bucle en curso mientras se descarta un ciclo concreto al producirse una condición es:
m = 20
for (k in 1:m) {
if (!k %% 2)
next
print(k)
}Este trozo de código imprime todos los números impares dentro del intervalo 1:m (aquí m=20). En otras palabras, se imprimirán todos los enteros excepto los que tengan resto no nulo al dividirlos por 2 (de ahí el uso del operando módulo %%), tal y como especifica la prueba if.
Los números cuyo resto sea cero no se imprimirán, ya que el programa salta a la evaluación de la condición i in 1:m e ignora cualquier instrucción que pudiera seguir. En este caso, se ignora print(k).
Conclusión sobre el uso de bucles en R
- Intenta poner el menor código posible dentro del bucle eliminando tantas instrucciones como sea posible. Recuerda que todo lo que esté dentro del bucle se repetirá varias veces y quizás no sea necesario.
- Tenga cuidado cuando utilice
repeat: asegúrese de que se establece explícitamente una terminación mediante la comprobación de una condición o puede acabar en un bucle infinito. - Es mejor utilizar una o más llamadas a funciones dentro del bucle si éste se está haciendo (demasiado) grande. Las llamadas a funciones facilitarán a otros usuarios el seguimiento del código. Pero el uso de un bucle for anidado para realizar operaciones con matrices o arrays es probablemente una señal de que no has implementado las cosas de la mejor manera para un lenguaje basado en matrices como R.
- No se recomienda "hacer crecer" la variable o el conjunto de datos utilizando una asignación en cada iteración. En algunos lenguajes como Matlab, se emite un error de advertencia: puede continuar, pero se le invita a considerar alternativas. En la siguiente sección se muestra un ejemplo típico.
Cuándo utilizar bucles R
Todo esto está muy bien, pero ¿cuándo hay que utilizar bucles en R y cuándo no?
Cada vez que haya que repetir alguna(s) operación(es), un bucle puede resultar útil.
Sólo hay que especificar cuántas veces o en qué condiciones deben ejecutarse esas operaciones: se asignan valores iniciales a una variable del bucle de control, se ejecuta el bucle y, una vez finalizado, se suele hacer algo con los resultados.
Pero, ¿cuándo hay que utilizar los bucles?
¿No podría replicar la instrucción deseada el número suficiente de veces?
Bueno, una regla general podría ser que si necesitas realizar una acción (digamos) tres veces o más, entonces un bucle te serviría mejor. Esto hace que el código sea más compacto, legible y fácil de mantener, y puede ahorrar algo de mecanografía: digamos que descubre que una determinada instrucción debe repetirse una vez más de lo previsto inicialmente: en lugar de reescribir la instrucción completa, puede simplemente alterar el valor de una variable en la condición de prueba.
Sin embargo, la peculiar naturaleza de R sugiere no utilizar bucles en absoluto (¡!) siempre que existan alternativas.
Por suerte, ¡hay algunas alternativas!
R disfruta de una característica que pocos lenguajes de programación tienen, que se llama vectorización.
Alternativas a los bucles en R
¿Qué es la vectorización?
Como sugiere la palabra, la vectorización es la operación de convertir operaciones repetidas sobre números simples ("escalares") en operaciones únicas sobre vectores o matrices. Ya ha visto varios ejemplos en las subsecciones anteriores.
Ahora bien, un vector es la estructura de datos elemental en R y es "una entidad única que consiste en una colección de cosas", según el manual base de R.
Así, una colección de números es un vector numérico.
Si se combinan vectores (de la misma longitud), se obtiene una matriz. Puede hacerlo vertical u horizontalmente, utilizando diferentes instrucciones R. Así, en R, una matriz se ve como una colección de vectores horizontales o verticales. Por extensión, se pueden vectorizar operaciones repetidas sobre vectores.
Muchas de las construcciones de bucle anteriores pueden hacerse implícitas utilizando la vectorización.
Digo "implícitas", porque en realidad no desaparecen. En un nivel inferior, la forma vectorizada alternativa se traduce en código que contendrá uno o más bucles en el lenguaje de nivel inferior en el que se implementó y compiló la forma (Fortran, C o C++ ).
Éstas están ocultas para el usuario y suelen ser más rápidas que el código R explícito equivalente, pero a menos que esté planeando implementar sus propias funciones R utilizando uno de esos lenguajes, esto es totalmente transparente para usted.
El caso más elemental en el que se puede pensar es la suma de dos vectores v1 y v2 en un vector v3, que se puede hacer elemento a elemento con un bucle for:
v1 <- c(3,4,5)
v2 <- c(3,4,6)
v3 <- c(0,0,0)
n = length(v1)
for (i in 1:n) {
v3[i] <- v1[i] + v2[i]
}
v3También puede utilizar la forma vectorizada "nativa":
v3 = v1 + v2
v3Tenga en cuenta que dice "nativo" porque R puede reconocer todos los operadores aritméticos como actuando sobre vectores y matrices.
Del mismo modo, para dos matrices A y B, en lugar de sumar los elementos de A[i,j] y B[i,j] en las posiciones correspondientes, para lo cual hay que ocuparse de dos índices i y j, se le dice a R que haga lo siguiente:
A <- matrix(1:6, nrow = 3, ncol = 2)
B <- matrix(c(2,4,3,1,5,7), nrow=3, ncol=2)
C= A + B
CY esto es muy sencillo.
Explicación de la vectorización en R
¿Por qué la vectorización es más rápida si el número de operaciones elementales es aparentemente el mismo?
Esto se explica mejor si nos fijamos en las tuercas internas y los pernos de R, que requeriría un post aparte, pero de manera sucinta: en primer lugar, R es un lenguaje interpretado y, como tal, todos los detalles sobre la definición de variables son atendidos por el intérprete. No es necesario especificar que un número es de coma flotante ni asignar memoria utilizando un puntero en memoria, por ejemplo.
El intérprete de R "entiende" estas cuestiones a partir del contexto a medida que usted introduce sus comandos, pero lo hace comando a comando. Por lo tanto, tendrá que ocuparse de esas definiciones cada vez que emita una orden determinada, aunque sólo la repita.
Un compilador, en cambio, resuelve literalmente todas las definiciones y declaraciones en tiempo de compilación sobre todo el código; éste se traduce a un código binario compacto y optimizado, antes de que intentes ejecutar nada. Ahora, como las funciones de R están escritas en uno de estos lenguajes de bajo nivel, son más eficientes.
En la práctica, si uno mirara el código de bajo nivel, descubriría llamadas a C o C++, normalmente implementadas dentro de lo que se denomina un código envoltorio.
En segundo lugar, en los lenguajes que soportan la vectorización (como R o Matlab), cada instrucción que hace uso de un dato numérico, actúa sobre un objeto que está definido nativamente como un vector, aunque sólo esté formado por un elemento. Este es el valor predeterminado cuando se define, por ejemplo, una única variable numérica: su representación interna en R siempre será un vector, a pesar de estar formado por un único número.
Los bucles siguen existiendo bajo el capó, pero a un nivel de compilación C/C++ inferior y mucho más rápido. La ventaja de tener un vector es que las definiciones son resueltas por el intérprete una sola vez, sobre todo el vector, independientemente de su tamaño, en contraste con un bucle realizado sobre un escalar, donde las definiciones y asignaciones deben hacerse elemento por elemento, y esto es más lento.
Por último, tratar con formato vectorial nativo permite utilizar rutinas de Álgebra Lineal muy eficientes (como BLAS o Subprogramas Básicos de Álgebra Lineal), de forma que al ejecutar instrucciones vectorizadas, R aprovecha estas eficientes rutinas numéricas. Así que el mensaje sería, si es posible, procesar estructuras de datos enteras dentro de una única llamada a una función para evitar todas las operaciones de copia que se ejecutan.
Pero basta de divagaciones, vamos a hacer un ejemplo general de vectorización, y luego en la siguiente subsección, nos sumergiremos en funciones vectorizadas de R más específicas y populares para sustituir bucles.
Un ejemplo de vectorización en R
Volvamos a la noción de "datos crecientes", una forma típicamente ineficiente de "actualizar" un marco de datos.
En primer lugar, se crea una matriz m x n con replicate(m, rnorm(n)) con m=10 vectores columna de n=10 elementos cada uno, construidos con rnorm(n), que crea números normales aleatorios.
A continuación, se transforma en un marco de datos (por tanto, 10 observaciones de variables 10 ) y se realiza una operación algebraica en cada elemento mediante un bucle anidado for: en cada iteración, una función sinusoidal incrementa cada elemento al que se refieren los dos índices.
El siguiente ejemplo es un poco artificial, pero podría representar la adición de una señal a un ruido aleatorio:
# This is a bad loop with 'growing' data
set.seed(42)
m = 10
n = 10
# Create matrix of normal random numbers
mymat <- replicate(m, rnorm(n))
# Transform into data frame
mydframe <- data.frame(mymat)
for (i in 1:m) {
for (j in 1:n) {
mydframe[i, j] <- mydframe[i, j] + 10 * sin(0.75 * pi)
print(mydframe)
}
}Aquí, la mayor parte del tiempo de ejecución consiste en copiar y gestionar el bucle.
Veamos cómo es una solución vectorizada:
set.seed(42)
m = 10
n = 10
mymat <- replicate(m, rnorm(n))
mydframe <- data.frame(mymat)
mydframe <- mydframe + 10 * sin(0.75 * pi)
mydframeEsto parece más sencillo: la última línea sustituye al bucle anidado for. Obsérvese el uso de set.seed() para garantizar que las dos implementaciones dan exactamente el mismo resultado.
Cuantifiquemos ahora el tiempo de ejecución de las dos soluciones.
Puede hacerlo utilizando comandos del sistema R, como system.time() al que se puede pasar un trozo de código como éste:
Consejo: sólo tiene que poner el código que desea evaluar entre los paréntesis de la función system.time().
# Insert `system.time()` to measure loop execution
for (i in 1:m) {
for (j in 1:n) {
mydframe[i, j] <- mydframe[i, j] + 10 * sin(0.75 * pi)
}
}
# Add `system.time()` to measure vectorized execution
mydframe <- mydframe + 10 * sin(0.75 * pi) En el trozo de código anterior, se hace el trabajo de elegir m y n, la creación de la matriz y su transformación en un marco de datos sólo una vez al principio, y luego se evalúa el trozo for contra el "one-liner" de la versión vectorizada con las dos llamadas separadas a system.time().
Se ve que ya con un ajuste mínimo de m=n=10 la versión vectorizada es 7 veces más rápida, aunque para valores tan bajos apenas tiene importancia para el usuario.
Las diferencias se hacen notables (a escala humana) si se pone m=n=100, mientras que aumentar a 1000 hace que el bucle for parezca colgado durante varias decenas de segundos, mientras que la forma vectorizada sigue funcionando en un abrir y cerrar de ojos.
Para m=n=10000 el bucle for se cuelga durante más de un minuto mientras que el vectorizado requiere 2,54 seg. Por supuesto, estas medidas deben tomarse a la ligera y dependerán de la configuración de hardware y software, posiblemente evitando sobrecargar el portátil con unas decenas de pestañas abiertas en el navegador de Internet y varias aplicaciones ejecutándose en segundo plano; pero estas medidas son ilustrativas de las diferencias.
Para ser justos, el aumento de m y n afecta gravemente también a la generación de la matriz, como puede verse fácilmente colocando otra llamada a system.time() alrededor de la función de replicación.
Le invitamos a jugar con m y n para ver cómo cambia el tiempo de ejecución, trazando el tiempo de ejecución en función del producto m x n. Este es el indicador relevante, porque expresa la dimensión de las matrices creadas. De este modo, también cuantifica el número de iteraciones necesarias para completar la tarea a través del bucle nset-ed for.
Este es un ejemplo de vectorización. Pero hay muchos otros. En R News, un boletín del proyecto R en la página 46, hay funciones muy eficientes para calcular sumas y medias para ciertas dimensiones en matrices o arrays, como: rowSums(), colSums(), rowMeans(), y colMeans().
Además, el boletín también menciona que "...las funciones de la familia 'apply', denominadas [s,l,m,t]apply, se proporcionan para aplicar otra función a los elementos/dimensiones de los objetos. Estas funciones 'apply' proporcionan una sintaxis compacta para tareas a veces bastante complejas que resulta más legible y rápida que los bucles mal escritos".
La familia apply: ¿sólo bucles ocultos?
La riquísima y potente familia de funcionesapply está formada por funciones intrínsecamente vectorizadas. Si a primera vista no parecen contener ningún bucle, esta característica se pone de manifiesto cuando se mira detenidamente bajo el capó.
El comando apply, o más bien familia de comandos, pertenece al paquete base de R. Está dotado de una serie de funciones (la [s,l,m,r, t,v]apply) para manipular trozos de datos en forma de matrices o arrays de forma repetitiva, permitiendo cruzar o recorrer los datos y evitando el uso explícito de construcciones de bucle. Las funciones actúan sobre una matriz o matriz de entrada y aplican una función de nombre elegido con uno o varios argumentos opcionales .
Nótese que por eso pertenecen a los llamados "funcionales" (como en la página de R avanzado de Hadley Wickham).
La función llamada puede ser una función de agregación, como una media simple, u otra función de transformación o subconjunto.
Hay que señalar que la aplicación de estas funciones no conduce necesariamente a una ejecución más rápida: las diferencias no son enormes; más bien evita la codificación de bucles engorrosos, reduciendo la posibilidad de errores.
Las funciones dentro de la familia son: apply(), sapply(), lapply(), mapply(), rapply(), tapply(), vapply().
Pero, ¿cuándo y cómo utilizarlos?
Cabe destacar que un paquete como plyr cubre la funcionalidad de la familia; aunque recordarlas todas sin recurrir a la documentación oficial puede resultar difícil, aun así estas funciones forman la base de combinaciones más complejas y útiles.
Los tres primeros son los más utilizados:
apply()
Desea aplicar una función determinada a las filas (índice "1") o columnas (índice "2") de una matriz. Consulte esta página para obtener más información.
lapply()
Desea aplicar una función dada a cada elemento de una lista y obtener una lista como resultado (lo que explica la "l" del nombre de la función). Lea sobre esta función en la documentación de R.
sapply()
Desea aplicar una función dada a cada elemento de una lista, pero desea obtener un vector en lugar de una lista. ¿Necesita saber más? Visite la página de documentación de R.
Las funciones relacionadas son sweep(), by() y aggregate() y se utilizan ocasionalmente junto con los elementos de la familia apply().
Limito la discusión de esta entrada de blog a la función apply() (una discusión más extensa sobre este tema podría ser el centro de una futura entrada).
Dada una matriz M, la llamada apply(M,1,fun) o apply(M, 2,fun) aplicará la función fun especificada a las filas de M, si se especifica 1; o a las columnas de M, si se especifica 2. Este argumento numérico se denomina "margen" y está limitado a los valores 1 y 2 porque la función opera sobre una matriz. Sin embargo, puedes tener un array de hasta 8 dimensiones.
La función puede ser cualquier función válida de R, pero podría ser una Función Definida por el Usuario (UDF), incluso codificada dentro de apply(), lo cual es práctico.
apply()un ejemplo
# define matrix `mymat` by replicating the sequence `1:5` for `4` times and transforming into a matrix
mymat <- matrix(rep(seq(5), 4), ncol = 5)
# `mymat` sum on rows
apply(mymat, 1, sum)
# `mymat` sum on columns
apply(mymat, 2, sum)
# With user defined function within the apply that adds any number `y` to the sum of the row
# `y` is set at `4.5`
apply(mymat, 1, function(x, y)
sum(x) + y, y = 4.5)
# Or produce a summary column wise for each column
apply(mymat, 2, function(x, y)
summary(mymat))Usted utiliza marcos de datos con frecuencia: en este caso concreto, debe asegurarse de que los datos tienen el mismo tipo o, de lo contrario, pueden producirse conversiones forzadas de tipo de datos, que probablemente no es lo que desea. Por ejemplo, en un marco de datos mixto de texto y números, los datos numéricos se convertirán en cadenas o caracteres.
Consideraciones finales sobre el uso y las alternativas a los bucles en R
Así pues, este viaje nos ha llevado desde las construcciones de bucle fundamentales utilizadas en programación hasta la noción (básica) de vectorización y a un ejemplo del uso de una de las funciones de la familia apply(), que aparecen con frecuencia en R.
En cuanto al control del flujo de código, sólo se han tratado los bucles: for, while, repeat y la forma de interrumpirlos y salir de ellos.
Como las últimas subsecciones insinúan que los bucles en R deben evitarse, puede que te preguntes por qué demonios deberías aprender sobre ellos.
Ahora, en mi opinión, deberías aprender estas estructuras de programación porque:
- Es probable que R no sea tu único lenguaje en la ciencia de datos o en cualquier otro lugar, y comprender construcciones generales como los bucles es algo útil para poner en tu propia bolsa de habilidades. La sintaxis de los bucles puede variar en función del lenguaje, pero una vez que los domines en uno, los aplicarás fácilmente a cualquier otro lenguaje con el que te encuentres.
- El universo R es enorme y es muy difícil, si no imposible, conocer todas las funciones R existentes. Hay muchas formas de hacer las cosas, algunas más eficientes o elegantes que otras, y tu curva de aprendizaje será incremental; cuando las utilices, empezarás a preguntarte por formas más eficientes de hacer las cosas y acabarás aterrizando en funciones de las que nunca antes habías oído hablar. Para cuando usted lea esto, se habrán desarrollado unas cuantas bibliotecas nuevas, se habrán publicado otras, por lo que la posibilidad de conocerlas todas es escasa, a menos que se pase todo el tiempo como especialista en R.
- Por último, al menos cuando no se trata de conjuntos de datos de dimensiones particularmente elevadas, una solución de bucle sería fácil de codificar y leer. Y quizás, como científico de datos, se le pida que cree un prototipo de un trabajo único que simplemente funcione. Quizá no le interesen las formas sofisticadas o elegantes de obtener un resultado. Tal vez, en el flujo de trabajo de análisis de datos, sólo tenga que demostrar su experiencia en el campo y concentrarse en el contenido. Otra persona, probablemente un especialista en back-end, se encargará de la fase de producción (¡y puede que codifique en otro idioma!).
Si los bucles for en R ya no suponen un reto para usted después de leer este tutorial, podría considerar la posibilidad de realizar el curso R Intermedio de DataCamp. Este curso reforzará sus conocimientos de los temas de R Intermedio con un montón de ejercicios nuevos y divertidos. Sin embargo, si los bucles ya no tienen secretos para ti, el curso Writing Functions in R de DataCamp, impartido por Hadley y Charlotte Wickham, podría interesarte. Consulte también el tutorial sobre bucles For en R.
Ejecuta y edita el código de este tutorial en línea
Ejecutar códigoPreguntas frecuentes sobre los bucles R
¿Qué son los bucles en R y por qué son útiles?
Los bucles permiten repetir un bloque de código varias veces. Son útiles cuando se desea realizar la misma acción en varios puntos de datos u objetos, o cuando se desea repetir una acción hasta que se cumpla una determinada condición.
¿Cuáles son los distintos tipos de bucles en R?
Existen dos tipos principales de bucles en R: los bucles for y los bucles while.
- Los bucles For repiten un bloque de código para cada elemento de una lista o secuencia. Por ejemplo, puede utilizar un bucle for para imprimir todos los elementos de un vector, o para aplicar una función a cada elemento de una lista.
- Los bucles while repiten un bloque de código mientras se cumpla una determinada condición. Por ejemplo, puede utilizar un bucle while para seguir preguntando al usuario hasta que introduzca una respuesta válida.
¿Cómo se detiene un bucle en R?
Para detener un bucle en R, puede utilizar la sentencia break. Esto saldrá inmediatamente del bucle y continuará con el resto del código.
¿Cómo salto a la siguiente iteración de un bucle en R?
Para pasar a la siguiente iteración de un bucle en R, puede utilizar la sentencia next. Esto saltará el resto de la iteración actual y pasará a la siguiente.
¿Puedo poner bucles dentro de otros bucles en R?
Sí, en R se pueden poner bucles dentro de otros bucles, lo que se denomina "anidamiento" de bucles. Por ejemplo, puede utilizar un bucle for dentro de otro bucle for para iterar sobre los elementos de una matriz.
