Latent Semantic Analysis using Python

Discovering topics are beneficial for various purposes such as for clustering documents, organizing online available content for information retrieval and recommendations. Multiple content providers and news agencies are using topic models for recommending articles to readers. Similarly recruiting firms are using in extracting job descriptions and mapping them with candidate skill set. If you see the data scientist job, which is all about extracting the ‘knowledge’ from a large amount of collected data. Usually, collected data is unstructured. You need powerful tools and techniques to analyze and understand a large amount of unstructured data.

Topic modeling is a text mining technique which provides methods for identifying co-occurring keywords to summarize large collections of textual information. It helps in discovering hidden topics in the document, annotate the documents with these topics, and organize a large amount of unstructured data.

Topic Modeling

Topic Modeling automatically discover the hidden themes from given documents. It is an unsupervised text analytics algorithm that is used for finding the group of words from the given document. These group of words represents a topic. There is a possibility that, a single document can associate with multiple themes. for example, a group words such as 'patient', 'doctor', 'disease', 'cancer', ad 'health' will represents topic 'healthcare'. Topic Modeling is a different game compared to rule-based text searching that uses regular expressions.

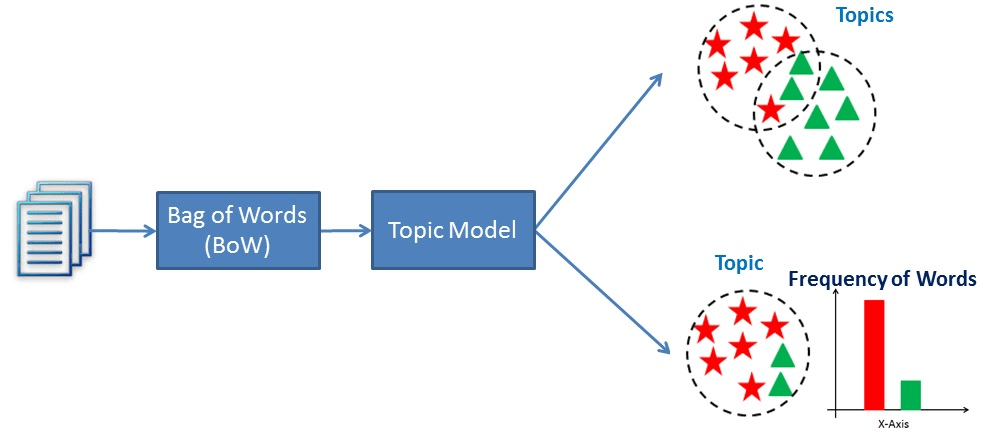
Comparison Between Text Classification and Topic Modeling

Text classification is a supervised machine learning problem, where a text document or article classified into a pre-defined set of classes. Topic modeling is the process of discovering groups of co-occurring words in text documents. These group co-occurring related words makes "topics". It is a form of unsupervised learning, so the set of possible topics are unknown. Topic modeling can be used to solve the text classification problem. Topic modeling will identify the topics presents in a document" while text classification classifies the text into a single class.

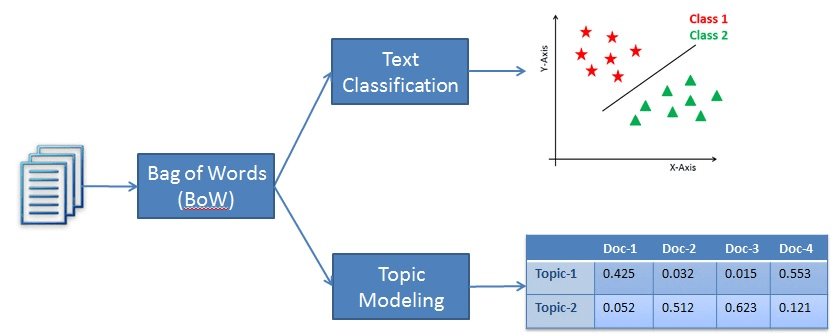
Latent Semantic Analysis

LSA (Latent Semantic Analysis) also known as LSI (Latent Semantic Index) LSA uses bag of word(BoW) model, which results in a term-document matrix(occurrence of terms in a document). Rows represent terms and columns represent documents. LSA learns latent topics by performing a matrix decomposition on the document-term matrix using Singular value decomposition. LSA is typically used as a dimension reduction or noise reducing technique.

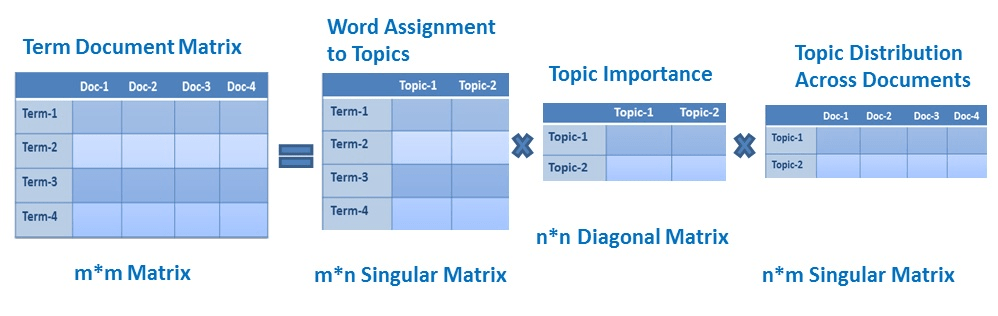
Singular Value Decomposition(SVD)

SVD is a matrix factorization method that represents a matrix in the product of two matrices. It offers various useful applications in signal processing, psychology, sociology, climate, and atmospheric science, statistics and astronomy.

• M is an m×m matrix
• U is a m×n left singular matrix
• Σ is a n×n diagonal matrix with non-negative real numbers.
• V is a m×n right singular matrix
• V* is n×m matrix, which is the transpose of the V.

Identity matrix: It is a square matrix in which all the elements of the principal diagonal are ones, and all other elements are zeros.

Diagonal Matrix: It is a matrix in which the entries other than the main diagonal are all zero.

Singular Matrix: A matrix is singular if its determinant is 0 or a square matrix that does not have a matrix inverse.

Determining Optimum Number of Topics

What is the best way to determine k (number of topics) in topic modeling? Identify the optimum number of topics in the given corpus text is a challenging task. We can use the following options for determining the optimum number of topics:

• One way to determine the optimum number of topics is to consider each topic as a cluster and find out the effectiveness of a cluster using the Silhouette coefficient.
• Topic coherence measure is a realistic measure for identifying the number of topics.

Topic Coherence measure is a widely used metric to evaluate topic models. It uses the latent variable models. Each generated topic has a list of words. In topic coherence measure, you will find average/median of pairwise word similarity scores of the words in a topic. The high value of topic coherence score model will be considered as a good topic model.

Implementing LSA using Gensim

Import the required library

#import modules
import os.path
from gensim import corpora
from gensim.models import LsiModel
from nltk.tokenize import RegexpTokenizer
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from gensim.models.coherencemodel import CoherenceModel
import matplotlib.pyplot as plt

Loading Data

Let's first create data load function for loading articles.csv. You can download the data here.

def load_data(path,file_name):
    """
    Input  : path and file_name
    Purpose: loading text file
    Output : list of paragraphs/documents and
             title(initial 100 words considred as title of document)
    """
    documents_list = []
    titles=[]
    with open( os.path.join(path, file_name) ,"r") as fin:
        for line in fin.readlines():
            text = line.strip()
            documents_list.append(text)
    print("Total Number of Documents:",len(documents_list))
    titles.append( text[0:min(len(text),100)] )
    return documents_list,titles

Preprocessing Data

After data loading function, you need to preprocess the text. Following steps are taken to preprocess the text:

• Tokenize the text articles
• Remove stop words
• Perform stemming on text artcle

def preprocess_data(doc_set):
    """
    Input  : docuemnt list
    Purpose: preprocess text (tokenize, removing stopwords, and stemming)
    Output : preprocessed text
    """
    # initialize regex tokenizer
    tokenizer = RegexpTokenizer(r'\w+')
    # create English stop words list
    en_stop = set(stopwords.words('english'))
    # Create p_stemmer of class PorterStemmer
    p_stemmer = PorterStemmer()
    # list for tokenized documents in loop
    texts = []
    # loop through document list
    for i in doc_set:
        # clean and tokenize document string
        raw = i.lower()
        tokens = tokenizer.tokenize(raw)
        # remove stop words from tokens
        stopped_tokens = [i for i in tokens if not i in en_stop]
        # stem tokens
        stemmed_tokens = [p_stemmer.stem(i) for i in stopped_tokens]
        # add tokens to list
        texts.append(stemmed_tokens)
    return texts

Prepare Corpus

Next step is to prepare corpus. Here, you need to create a document-term matrix and dictionary of terms.

def prepare_corpus(doc_clean):
    """
    Input  : clean document
    Purpose: create term dictionary of our courpus and Converting list of documents (corpus) into Document Term Matrix
    Output : term dictionary and Document Term Matrix
    """
    # Creating the term dictionary of our courpus, where every unique term is assigned an index. dictionary = corpora.Dictionary(doc_clean)
    dictionary = corpora.Dictionary(doc_clean)
    # Converting list of documents (corpus) into Document Term Matrix using dictionary prepared above.
    doc_term_matrix = [dictionary.doc2bow(doc) for doc in doc_clean]
    # generate LDA model
    return dictionary,doc_term_matrix

Create an LSA model using Gensim

After corpus creation, you can generate a model using LSA.

def create_gensim_lsa_model(doc_clean,number_of_topics,words):
    """
    Input  : clean document, number of topics and number of words associated with each topic
    Purpose: create LSA model using gensim
    Output : return LSA model
    """
    dictionary,doc_term_matrix=prepare_corpus(doc_clean)
    # generate LSA model
    lsamodel = LsiModel(doc_term_matrix, num_topics=number_of_topics, id2word = dictionary)  # train model
    print(lsamodel.print_topics(num_topics=number_of_topics, num_words=words))
    return lsamodel

Determine the number of topics

Another extra step needs to be taken to optimize results by identifying an optimum amount of topics. Here, you will generate coherence scores to determine an optimum number of topics.

def compute_coherence_values(dictionary, doc_term_matrix, doc_clean, stop, start=2, step=3):
    """
    Input   : dictionary : Gensim dictionary
              corpus : Gensim corpus
              texts : List of input texts
              stop : Max num of topics
    purpose : Compute c_v coherence for various number of topics
    Output  : model_list : List of LSA topic models
              coherence_values : Coherence values corresponding to the LDA model with respective number of topics
    """
    coherence_values = []
    model_list = []
    for num_topics in range(start, stop, step):
        # generate LSA model
        model = LsiModel(doc_term_matrix, num_topics=number_of_topics, id2word = dictionary)  # train model
        model_list.append(model)
        coherencemodel = CoherenceModel(model=model, texts=doc_clean, dictionary=dictionary, coherence='c_v')
        coherence_values.append(coherencemodel.get_coherence())
    return model_list, coherence_values

Let's plot coherence score values.

def plot_graph(doc_clean,start, stop, step):
    dictionary,doc_term_matrix=prepare_corpus(doc_clean)
    model_list, coherence_values = compute_coherence_values(dictionary, doc_term_matrix,doc_clean,
                                                            stop, start, step)
    # Show graph
    x = range(start, stop, step)
    plt.plot(x, coherence_values)
    plt.xlabel("Number of Topics")
    plt.ylabel("Coherence score")
    plt.legend(("coherence_values"), loc='best')
    plt.show()

start,stop,step=2,12,1
plot_graph(clean_text,start,stop,step)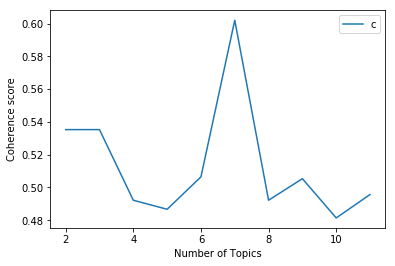

You can easily evaluate this graph. Here, you have a number of topics on X-axis and coherence score on Y-axis. Of the number of topics, 7 have the highest coherence score, so the optimum number of topics are 7.

Run all the above functions

# LSA Model
number_of_topics=7
words=10
document_list,titles=load_data("","articles.txt")
clean_text=preprocess_data(document_list)
model=create_gensim_lsa_model(clean_text,number_of_topics,words)

Total Number of Documents: 4551
[(0, '0.361*"trump" + 0.272*"say" + 0.233*"said" + 0.166*"would" + 0.160*"clinton" + 0.140*"peopl" + 0.136*"one" + 0.126*"campaign" + 0.123*"year" + 0.110*"time"'), (1, '-0.389*"citi" + -0.370*"v" + -0.356*"h" + -0.355*"2016" + -0.354*"2017" + -0.164*"unit" + -0.159*"west" + -0.157*"manchest" + -0.116*"apr" + -0.112*"dec"'), (2, '0.612*"trump" + 0.264*"clinton" + -0.261*"eu" + -0.148*"say" + -0.137*"would" + 0.135*"donald" + -0.134*"leav" + -0.134*"uk" + 0.119*"republican" + -0.110*"cameron"'), (3, '-0.400*"min" + 0.261*"eu" + -0.183*"goal" + -0.152*"ball" + -0.132*"play" + 0.128*"said" + 0.128*"say" + -0.126*"leagu" + 0.122*"leav" + -0.122*"game"'), (4, '0.404*"bank" + -0.305*"eu" + -0.290*"min" + 0.189*"year" + -0.164*"leav" + -0.153*"cameron" + 0.143*"market" + 0.140*"rate" + -0.139*"vote" + -0.133*"say"'), (5, '0.310*"bank" + -0.307*"say" + -0.221*"peopl" + 0.203*"trump" + 0.166*"1" + 0.164*"min" + 0.163*"0" + 0.152*"eu" + 0.152*"market" + -0.138*"like"'), (6, '0.570*"say" + 0.237*"min" + -0.170*"vote" + 0.158*"govern" + -0.154*"poll" + 0.122*"tax" + 0.115*"statement" + 0.115*"bank" + 0.112*"budget" + -0.108*"one"')]

• Topic-1: "trump", "say", "said", "would", "clinton", "peopl", "one", "campaign","year","time"' (US Presidential Elections)
• Topic-2: "citi", "v", "h", "2016", "2017","unit", "west", "manchest","apr" ,"dec"'(English Premier League)
• Topic-3: "trump","clinton", "eu","say","would","donald","leav","uk" ,"republican" ,"cameron"(US Presidential Elections, Brexit)
• Topic-4:min","eu","goal","ball","play","said","say","leagu","leav","game"(English Premier League)
• Topic-5: "bank","eu","min","year","leav","cameron","market","rate","vote","say" (Brexit and Market Condition)
• Topic-6: "bank","say","peopl","trump","1" ,"min" ,"eu","market" ,"like"(Plitical situations and market conditions)
• Topic-7: "say","min","vote","govern","poll","tax","statement","bank","budget","one"(US Presidential Elections and Financial Planning)

Here, 7 Topics were discovered using Latent Semantic Analysis. Some of them are overlapping topics. For Capturing multiple meanings with higher accuracy we need to try LDA( latent Dirichlet allocation). I will leave this as excercise for you, try it out using Gensim and share your views.

Pros and Cons of LSA

LSA algorithm is the simplest method which is easy to understand and implement. It also offers better results compared to the vector space model. It is faster compared to other available algorithms because it involves document term matrix decomposition only.

Latent topic dimension depends upon the rank of the matrix so we can't extend that limit. LSA decomposed matrix is a highly dense matrix, so it is difficult to index individual dimension. LSA unable to capture the multiple meanings of words. It is not easier to implement compared to LDA( latent Dirichlet allocation). It offers lower accuracy than LDA.

Use-Cases of Topic Modeling

Simple applications in which this technique is used are documented clustering in text analysis, recommender systems, and information retrieval. More detailed use-cases of topic modeling are:

• Resume Summarization: It can help recruiters to evaluate resumes by a quick glance. They can reduce effort in filtering pile of resume.
• Search Engine Optimization: online articles, blogs, and documents can be tag easily by identifying the topics and associated keywords, which can improve optimize search results.
• Recommender System Optimization: recommender systems act as an information filter and advisor according to the user profile and previous history. It can help us to discover unvisited relevant content based on past visits.
• Improving Customer Support: Discovering relevant topics and associated keywords in customer complaints and feedback for examples product and service specifications, department, and branch details. Such information help company to directly rotated the complaint in respective department.
• In the healthcare industry, topic modeling can help us to extract useful and valuable information from unstructured medical reports. This information can be used for patients treatment and medical science research purpose.

Conclusion

In this tutorial, you covered a lot of details about Topic Modeling. You have learned what Topic Modeling is, what is Latent Semantic Analysis, how to build respective models, how to topics generated using LSA. Also, you covered some basic concepts such as the Singular Value Decomposition, topic coherence score.

Hopefully, you can now utilize topic modeling to analyze your own datasets. Thanks for reading this tutorial!

If you would like to learn more about Python, take DataCamp's Case Studies in Statistical Thinking course.