8 modelos de machine learning explicados en 20 minutos

Los modelos de machine learning son algoritmos que pueden identificar patrones o hacer predicciones sobre conjuntos de datos no vistos. A diferencia de los programas basados en reglas, estos modelos no tienen que codificarse explícitamente y pueden evolucionar con el tiempo a medida que entran nuevos datos en el sistema.

Este artículo te presentará los distintos tipos de problemas que pueden resolverse mediante machine learning. A continuación, conocerás los ocho algoritmos de machine learning más utilizados por los científicos de datos para resolver problemas empresariales. 

Al final de este artículo, estarás familiarizado con la teoría y la intuición matemática que hay detrás de estos modelos, junto con la forma de implementarlos utilizando la biblioteca Scikit-Learn en Python. 

Explicaremos conceptos complejos de machine learning en un lenguaje sencillo, y este artículo está recomendado para aspirantes a la ciencia de datos sin una sólida formación en matemáticas o estadística.

¿Por qué utilizar modelos de machine learning?

Hoy en día, muchas grandes organizaciones utilizan alguna forma de modelización predictiva para maximizar los ingresos e impulsar el crecimiento empresarial.

El machine learning tiene una gran variedad de usos en distintos ámbitos. Las plataformas por suscripción como Netflix y Spotify, por ejemplo, utilizan machine learning para recomendar contenidos basándose en la actividad del usuario en la aplicación. 

Los sistemas de recomendación añaden valor empresarial directo a estas empresas, ya que una mejor experiencia de usuario hará más probable que los clientes sigan suscribiéndose a la plataforma. Es un ejemplo de modelo de machine learning no supervisado.

Del mismo modo, un proveedor de servicios móviles podría utilizar el machine learning para analizar la opinión de los usuarios y adaptar su oferta de productos a la demanda del mercado. Es un ejemplo de modelo de machine learning supervisado.

Todos los modelos de machine learning pueden clasificarse como supervisados o no supervisados. La mayor diferencia entre ambos es que un algoritmo supervisado requiere datos de entrenamiento de entrada y salida etiquetados, mientras que un modelo no supervisado puede procesar conjuntos de datos sin etiquetar.

Los modelos supervisados de machine learning pueden clasificarse a su vez en algoritmos de regresión y de clasificación, que se explicarán con más detalle en este artículo.

Modelos de regresión de machine learning

Los algoritmos de regresión se utilizan para predecir un resultado continuo (y) utilizando variables independientes (x). 

Por ejemplo, mira la tabla siguiente:

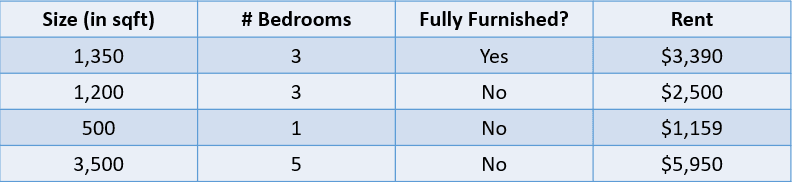
Imagen del autor

En este caso, nos gustaría predecir el alquiler de una casa en función de su tamaño, el número de habitaciones y si está totalmente amueblada. La variable dependiente, “Rent”, es numérica, por lo que se trata de un problema de regresión. 

Un problema con muchas variables de entrada como el anterior se denomina problema de regresión multivariante.

Métricas de regresión

Un error común entre los principiantes en la ciencia de datos es que un modelo de regresión puede evaluarse utilizando una métrica como la precisión. La precisión es una métrica utilizada para evaluar el rendimiento de los modelos de clasificación, como se explicará más adelante en este artículo.

Los modelos de regresión, por otra parte, se evalúan utilizando métricas como MAE (error absoluto medio), MSE (error cuadrático medio) y RMSE (raíz del error cuadrático medio).

Añadamos un valor predicho al problema anterior del precio de la vivienda y evaluemos estas predicciones utilizando algunas métricas de regresión:

Imagen del autor

1. Error absoluto medio: 

El error medio absoluto calcula la suma de la diferencia entre todos los valores verdaderos y los predichos, y la divide por el número total de observaciones. Aquí tienes la fórmula para calcular el MAE:

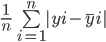
Calculemos el error absoluto medio de los valores anteriores utilizando esta fórmula:

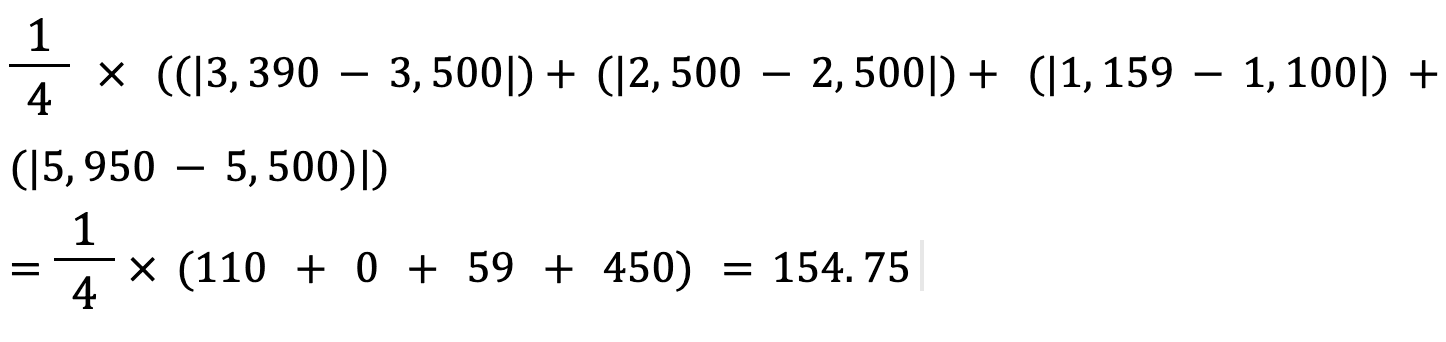
El error absoluto medio entre el precio de la vivienda real y el previsto es de aproximadamente 155 $.

2. Error cuadrático medio: 

La fórmula para calcular el error cuadrático medio de un modelo es similar a la de su error absoluto medio:

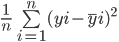
Observa que, mientras que el error medio absoluto calcula la distancia media absoluta entre el valor real y el predicho, el error medio al cuadrado halla la distancia media al cuadrado entre los valores real y predicho.

Calculemos el MSE entre los valores reales y los predichos anteriormente:

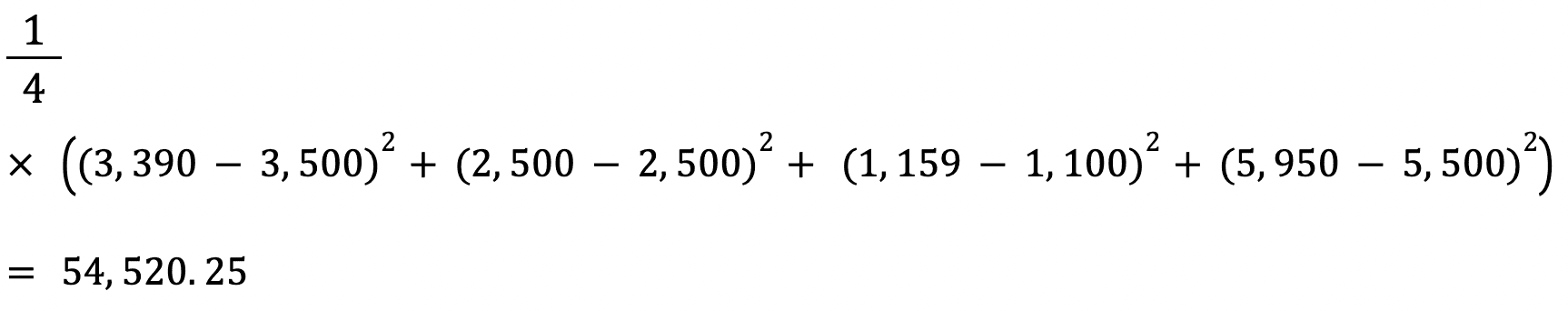
3. Raíz del error cuadrático medio: 

La RMSE de un estimador se calcula hallando la raíz cuadrada de su error cuadrático medio. Una ventaja de calcular el RMSE de un conjunto de datos frente a su MSE es que el error se devuelve en la misma unidad de la variable que estamos prediciendo.

En este caso, por ejemplo, el RMSE es √54 520,25=233,5. Este valor es interpretable, ya que está en función del precio de la vivienda, mientras que el error cuadrático medio no lo era.

Ahora que entiendes el concepto de regresión, veamos los distintos tipos de modelos de regresión:

Regresión lineal simple

La regresión lineal es un enfoque lineal para modelizar la relación entre una variable dependiente y una o más variables independientes. Este algoritmo consiste en encontrar la línea que mejor se ajuste a los datos disponibles. 

Aquí tienes una representación visual de cómo funciona un modelo de regresión lineal simple:

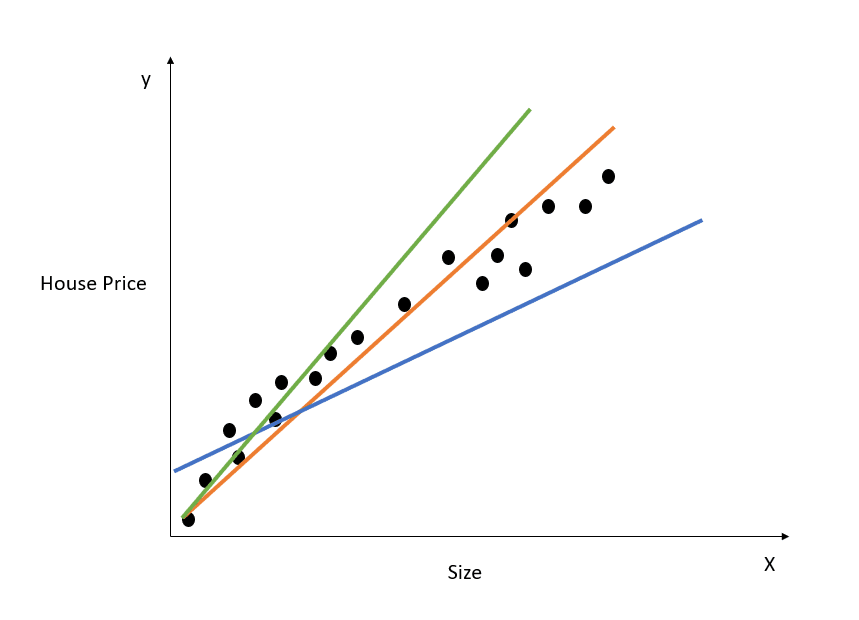
Imagen del autor

El gráfico anterior muestra la relación entre el precio y el tamaño de la vivienda. El modelo de regresión lineal creará la línea que mejor modele esta relación. Todas las predicciones del precio de la vivienda relativas a distintos valores del tamaño se situarán en la línea de mejor ajuste.

Observa que hay tres líneas dibujadas en el diagrama anterior. ¿Cuál de estas líneas es la "línea de mejor ajuste"?

Línea de mejor ajuste

Sólo con mirar el diagrama anterior, podemos ver que la línea naranja es la que más se aproxima a todos los puntos de datos mostrados. Por tanto, podemos decir intuitivamente que representa la "línea de mejor ajuste". 

Aquí tienes una explicación más formal de cómo se encuentra la línea de mejor ajuste en la regresión lineal:

La ecuación de una recta es y=mx+c. Aquí, m representa la pendiente de la recta y c representa su intercepción y. Hay infinitas formas de trazar esta línea, ya que hay infinitos valores posibles para m y c.

La línea de mejor ajuste, también conocida como línea de regresión por mínimos cuadrados, se encuentra minimizando la suma de la distancia al cuadrado entre los valores verdaderos y los predichos:

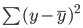
Puedes leer el tutorial Fundamentos de la regresión lineal en Python para comprender mejor el modelo de machine learning de regresión lineal y su aplicación.

Regresión Ridge

La regresión Ridge es una ampliación del modelo de regresión lineal explicado anteriormente. Es una técnica utilizada para mantener los coeficientes de un modelo de regresión lo más bajos posible.

Un problema de un modelo de regresión lineal simple es que sus coeficientes pueden llegar a ser grandes, lo que hace que el modelo sea más sensible a las entradas. Esto puede llevar a un sobreajuste.

Pongamos un ejemplo sencillo para entender el concepto de sobreajuste:

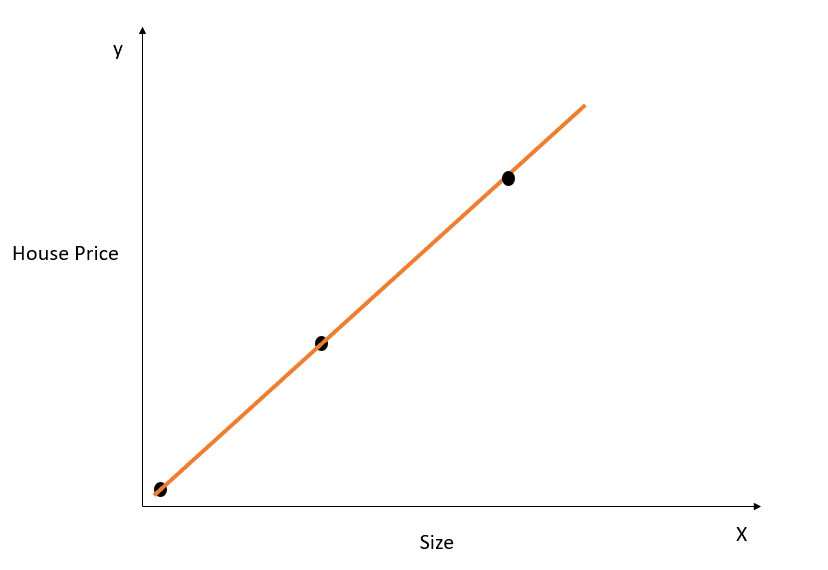
Imagen del autor

En la figura anterior, la recta de mejor ajuste anterior modela perfectamente la relación entre X e y, y la suma de la distancia al cuadrado entre los valores verdaderos y los predichos es 0. Recuerda que la ecuación de esta recta es y=mx+c.

Aunque esta línea se ajusta perfectamente al conjunto de datos de entrenamiento, probablemente no se generalizaría bien a los datos de prueba. Este fenómeno se denomina sobreajuste, y puedes leer este artículo sobre el sobreajuste para saber más sobre él.

En palabras sencillas, un modelo muy complejo captará matices innecesarios del conjunto de datos de entrenamiento que no se reflejan en el mundo real. Este modelo funcionará muy bien en los datos de entrenamiento, pero tendrá un rendimiento inferior en conjuntos de datos distintos de aquellos en los que fue entrenado.

Un modelo de regresión lineal con coeficientes grandes es propenso al sobreajuste.

La regresión Ridge es una técnica de regularización que obligará al algoritmo a elegir coeficientes más pequeños penalizando su función de pérdida para incluir un coste adicional.

Como se ha mostrado en el apartado anterior, éste es el error que queremos minimizar en la regresión lineal simple:

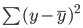
En la regresión Ridge, esta ecuación cambiará ligeramente, y se añadirá un término de penalización al error anterior:

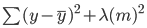
Observa que hay un valor (lambda) multiplicado a los coeficientes del modelo. Como este modelo sólo tiene una variable, hay un único coeficiente al que se añade un término de penalización. Si hay varias variables independientes, lambda se multiplicará por la suma de los coeficientes al cuadrado. 

Este término de penalización castiga al modelo por elegir coeficientes mayores. El objetivo es reducir los valores de los coeficientes para que las variables con una contribución menor al resultado tengan sus coeficientes próximos a 0. Esto reduce la varianza del modelo y ayuda a mitigar el sobreajuste.

¿Cuál es el valor lambda óptimo para la regresión Ridge?

Observa que un valor lambda de 0 no tendrá ningún efecto, y se elimina el término de penalización. Un valor más alto de lambda añadirá una mayor penalización por contracción, y los coeficientes del modelo se acercarán más a cero. 

Al elegir un valor lambda, asegúrate de encontrar un equilibrio entre la sencillez y un buen ajuste de los datos de entrenamiento. Un valor lambda más alto da lugar a un modelo sencillo y generalizado, pero elegir un valor demasiado alto conlleva el riesgo de un ajuste insuficiente. Por otra parte, elegir un valor de lambda muy próximo a cero puede dar lugar a un modelo muy complejo. 

Regresión Lasso

La regresión Lasso es otra extensión de la regresión lineal que reduce los coeficientes del modelo añadiendo un término de penalización a su función de costes.

Éste es el error que hay que minimizar en la regresión Lasso:

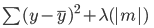
Observa que esta ecuación es como la de un modelo de regresión Ridge, salvo que, en lugar de multiplicar lambda por el cuadrado del coeficiente, la estamos multiplicando por el valor absoluto del coeficiente.

La mayor diferencia entre la regresión Ridge y la regresión Lasso es que en la regresión Ridge, aunque los coeficientes del modelo pueden reducirse hacia cero, en realidad nunca llegan a ser cero. En la regresión Lasso, es posible que los coeficientes del modelo sean cero. 

Si el coeficiente de una variable independiente llega a cero, la característica puede eliminarse del modelo. Esto reduce el espacio de características y hace que el algoritmo sea más fácil de interpretar, que es la mayor ventaja de la regresión Lasso. 

Debido a esto, la regresión Lasso también puede utilizarse como técnica de selección de rasgos, ya que las variables con poca importancia pueden tener coeficientes que lleguen a cero y se eliminarán por completo del modelo. 

Cómo construir un modelo de regresión de machine learning en Python

Puedes construir modelos de regresión lineal, Ridge y Lasso utilizando la biblioteca Scikit-Learn:

1. Regresión lineal

from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()

Para ajustar el modelo a tu conjunto de datos de entrenamiento, ejecuta

lr_model.fit(X_train,y_train)

2. Regresión Ridge

from sklearn.linear_model import Ridge
model = Ridge(alpha=1.0)

El término lambda se puede configurar mediante el parámetro "alfa" al definir el modelo. 

3. Regresión Lasso

from sklearn.linear_model import Lasso
model = Lasso(alpha=1.0)

Si quieres saber más sobre los modelos lineales y cómo construirlos en Python, sigue nuestro curso Introducción a la modelización lineal en Python.

Modelos de clasificación de machine learning

Utilizamos algoritmos de clasificación para predecir un resultado discreto (y) utilizando variables independientes (x). La variable dependiente, en este caso, es siempre una clase o categoría. 

Por ejemplo, predecir si un paciente tiene probabilidades de desarrollar una enfermedad cardiaca basándose en sus factores de riesgo es un problema de clasificación:

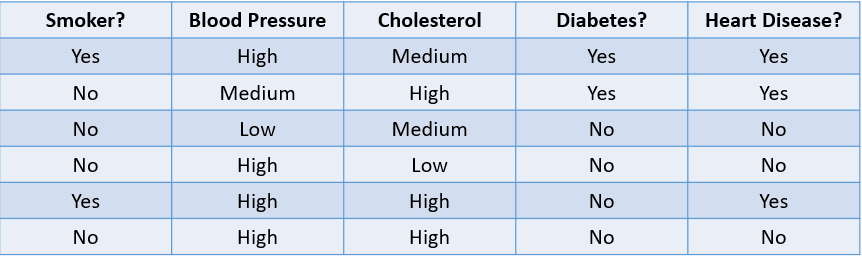
Imagen del autor

La tabla anterior muestra un problema de clasificación con cuatro variables independientes y una variable dependiente, la enfermedad cardiaca. Como sólo hay dos resultados posibles ("Yes" y "No"), se denomina problema de clasificación binaria. 

Otros ejemplos de problemas de clasificación binaria son clasificar si un correo electrónico es spam o legítimo, predecir la pérdida de clientes y decidir si conceder un préstamo a alguien.

Un problema de clasificación multiclase es aquel que tiene tres o más resultados posibles, como la predicción meteorológica o la distinción entre distintas especies animales.

Métricas de clasificación

Hay muchas formas de evaluar un modelo de clasificación. Aunque la precisión es la métrica más utilizada, no siempre es la más fiable.

Veamos algunos métodos habituales utilizados para evaluar un algoritmo de clasificación basándonos en el conjunto de datos que aparece a continuación:

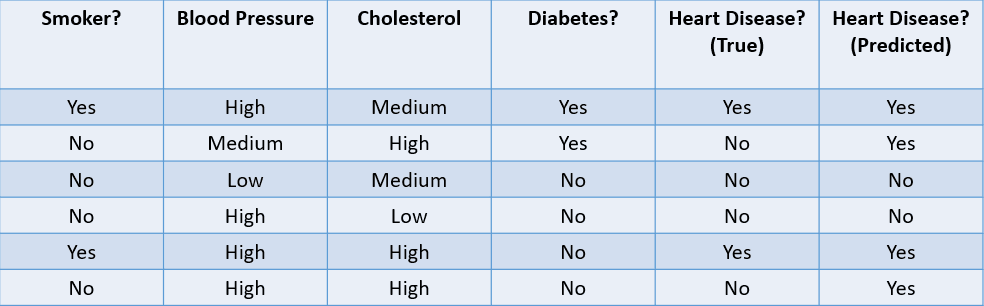
Imagen del autor

1. Fiabilidad: la fiabilidad puede definirse como la fracción de predicciones correctas realizadas por el modelo de machine learning.

La fórmula para calcular la fiabilidad es:

En este caso, la fiabilidad es de 46, es decir, 0,67.

2. Precisión: la precisión es una métrica utilizada para calcular la calidad de las predicciones positivas realizadas por el modelo. Se define como:

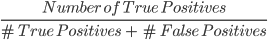
El modelo anterior tiene una precisión de 24, es decir, 0,5.

3. Exhaustividad: la exhaustividad se utiliza para calcular la calidad de las predicciones negativas realizadas por el modelo. Se define como:

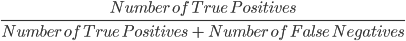
El modelo anterior tiene una exhaustividad de 2/2 ó 1.

Veamos un ejemplo sencillo para entender la diferencia entre precisión y exhaustividad:

Existe una enfermedad rara y mortal que afecta a una fracción de la población. El 95 % de los pacientes de la base de datos de un hospital no tienen la enfermedad, mientras que sólo el 5 % sí. Si construimos un algoritmo de machine learning que predice que nadie tiene la enfermedad, entonces la fiabilidad de entrenamiento de este modelo será del 95 %. A pesar de su gran fiabilidad, sabemos que no es un buen modelo, ya que no consigue identificar a los pacientes con la enfermedad.

Aquí es donde entran en juego métricas como la precisión y la exhaustividad. La precisión, o especificidad, nos indica la capacidad del modelo para identificar correctamente a las personas sin la enfermedad. La exhaustividad, o sensibilidad, nos dice lo bien que el modelo identifica a las personas con la enfermedad.

Un "buen" valor de precisión y exhaustividad es subjetivo y depende de tu caso de uso. 

En este escenario de predicción de la enfermedad, siempre queremos identificar a las personas con la enfermedad, aunque ello conlleve el riesgo de un falso positivo. Aquí, construiremos el modelo para que tenga mayor exhaustividad que precisión.

Por otra parte, si tuviéramos que construir un modelo que impidiera a los actores maliciosos entrar en un sitio web de comercio electrónico, quizá quisiéramos una mayor precisión, ya que bloquear a los usuarios legítimos provocaría una disminución de las ventas.

A menudo utilizamos una métrica llamada Puntuación F1 para hallar la media armónica de la precisión y la exhaustividad de un clasificador. En pocas palabras, la puntuación F1 combina la precisión y la exhaustividad en una sola métrica calculando su media. 

AUC, o Área bajo la curva, es otra métrica popular utilizada para medir el rendimiento de un modelo de clasificación. El AUC de un algoritmo nos habla de su capacidad para distinguir entre clases positivas y negativas.

Para saber más sobre medidas como la AUC y cómo se calculan, sigue el curso Aprendizaje supervisado en R de Datacamp.

Veamos ahora los distintos tipos de modelos de clasificación y cómo funcionan:

Regresión logística

La regresión logística es un modelo de clasificación simple que predice la probabilidad de que se produzca un suceso.

Aquí tienes un ejemplo de cómo funciona el modelo de regresión logística:

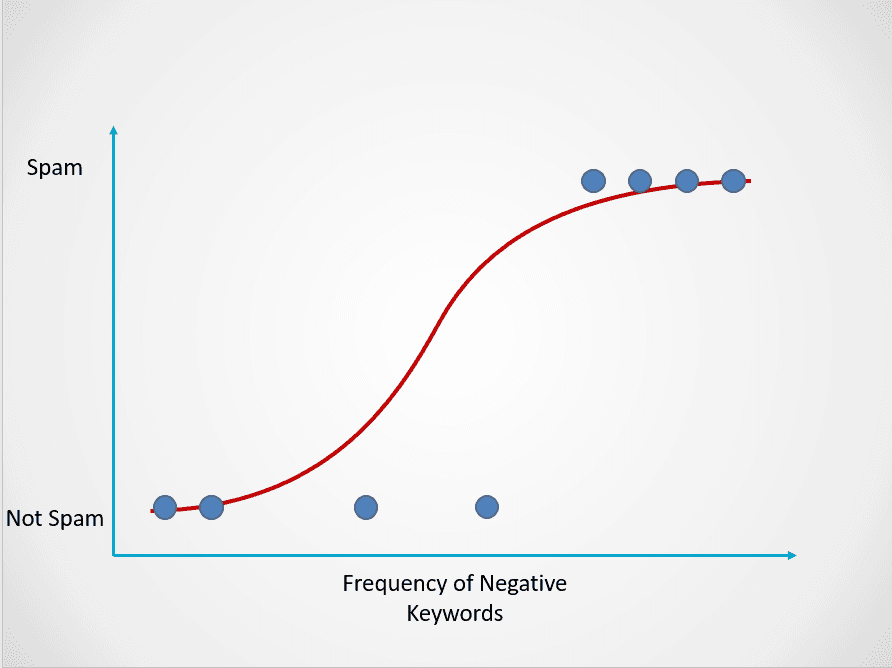
Imagen del autor

El gráfico anterior muestra una función logística que clasifica los datos de correo electrónico en dos categorías: "Spam" y "Not Spam" en función de la frecuencia de palabras clave negativas en su texto.

Observa que, a diferencia del algoritmo de regresión lineal, la regresión logística se modela con una curva en forma de S. Se conoce como función logística y tiene la siguiente fórmula:

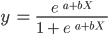
Mientras que la función lineal no tiene límite superior ni inferior, la función logística oscila entre 0 y 1. El modelo predice una probabilidad que va de 0 a 1, que determina la clase a la que pertenece el punto de datos.

En este ejemplo de correo spam, si el texto contiene pocas o ninguna palabra clave sospechosa, la probabilidad de que sea spam será baja y cercana a 0. Por otra parte, un correo electrónico con muchas palabras clave sospechosas tendrá una alta probabilidad de ser spam, cercana a 1.

Esta probabilidad se convierte entonces en un resultado de clasificación:

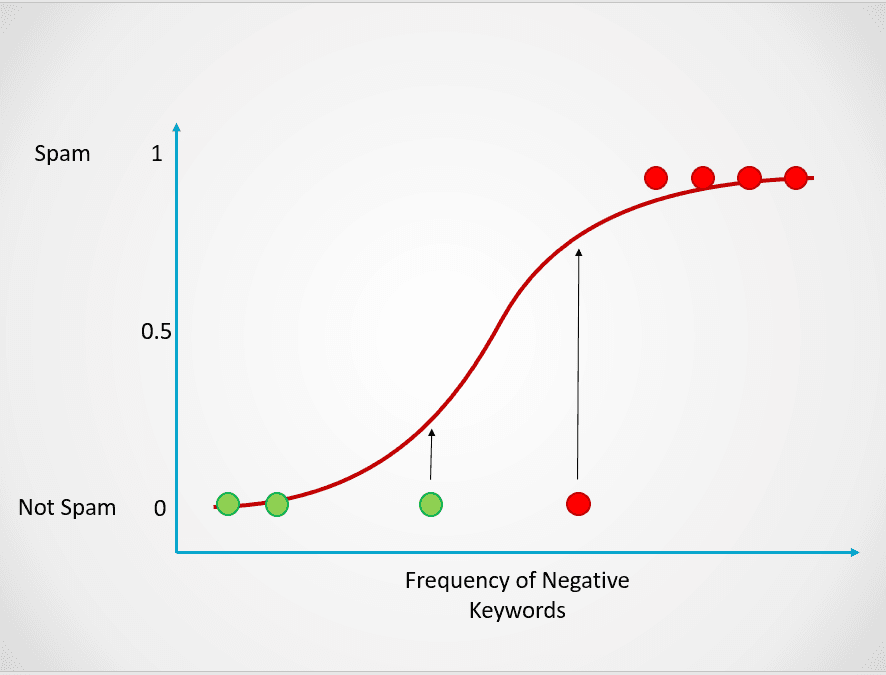
Imagen del autor

Todos los puntos coloreados en rojo tienen una probabilidad >= 0,5 de ser spam. Por lo tanto, se clasifican como spam y el modelo de regresión logística devolverá un resultado de clasificación de 1. Los puntos coloreados en verde tienen una probabilidad < 0,5 de ser spam, por lo que son clasificados por el modelo como "Not Spam" y devolverán un resultado de clasificación de 0.

Para problemas de clasificación binaria como el anterior, el umbral por defecto de un modelo de regresión logística es 0,5, lo que significa que a los puntos de datos con una probabilidad superior a 0,5 se les asignará automáticamente una etiqueta de 1. Este valor umbral puede modificarse manualmente en función de tu caso de uso para obtener mejores resultados.

Ahora, recuerda que en la regresión lineal, encontramos la línea de mejor ajuste minimizando la suma del error cuadrático entre los valores predichos y los verdaderos. En la regresión logística, sin embargo, los coeficientes se estiman utilizando una técnica llamada estimación de máxima verosimilitud en lugar de mínimos cuadrados.

Lee el tutorial de Python sobre regresión logística para saber más sobre el concepto de estimación de máxima verosimilitud y cómo funciona la regresión logística.

K vecinos más cercanos

KNN es un algoritmo de clasificación que clasifica un punto de datos en función del grupo al que pertenecen los puntos de datos más cercanos a él.

He aquí un ejemplo sencillo para demostrar cómo funciona el modelo K-Nearest Neighbors:

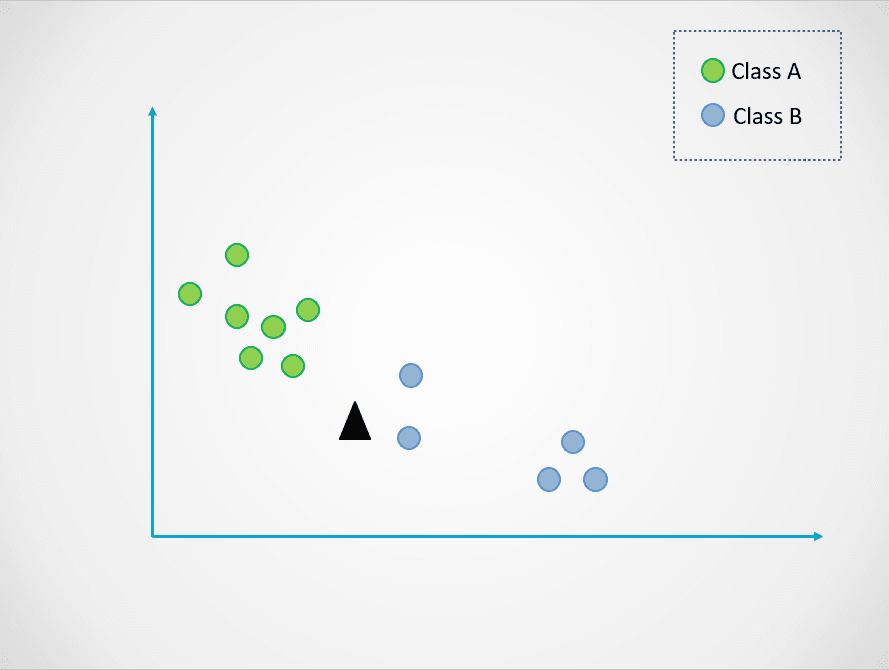
Imagen del autor

En el diagrama anterior, hay dos clases de puntos de datos: A y B. El triángulo negro representa un nuevo punto de datos que debe clasificarse en una de estas dos clases.

El algoritmo K-Nearest Neighbors funciona así:

• Paso 1: el modelo almacena primero todos los datos de entrenamiento.
• Paso 2: a continuación, calcula la distancia desde el nuevo punto de datos a todos los puntos del conjunto de datos.
• Paso 3: el modelo ordena estos puntos de datos en función de su distancia al nuevo punto de datos.
• Paso 4: el nuevo punto de datos se asigna a la clase de sus vecinos más próximos en función del valor de "k".

En la imagen anterior, el valor de k es 1. Esto significa que miramos sólo a un vecino más cercano al triángulo negro y asignamos el punto de datos a esa clase. El nuevo punto de datos es el más cercano al punto azul, por lo que lo asignamos a la clase B.

Ahora, modifiquemos el valor de k. Probemos con dos valores posibles de k, 3 y 7:

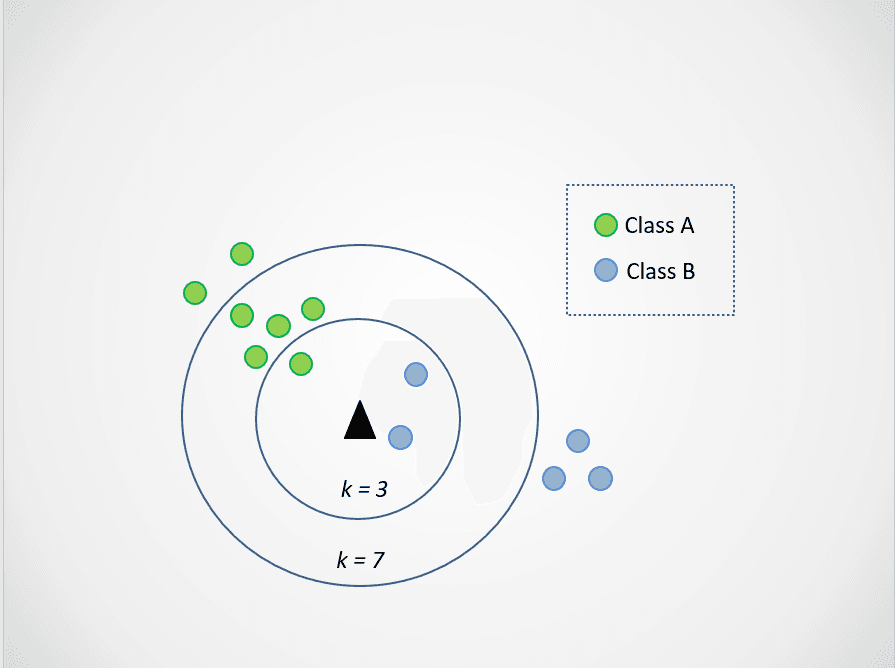
Imagen del autor

Ahora, observa que cuando elegimos k=3, el nuevo punto de datos está entre dos categorías. Esto significa que elegimos la clase mayoritaria. Dos vecinos más cercanos son azules, y un vecino más cercano es verde, por lo que el punto de datos se asignará de nuevo a la clase con puntos azules, la clase B.

Sin embargo, cuando k=7, las cosas cambian. Ahora, dos vecinos más cercanos son azules, y siete son verdes. En este caso, el punto de datos se asignará a la clase verde, la clase A.

Elegir distintos valores de k influirá en la clase a la que se asigne el nuevo punto. 

Seleccionar un valor demasiado pequeño puede ser ruidoso y estar sujeto a valores atípicos, mientras que seleccionar un valor grande puede hacer que pases por alto categorías con menos puntos de datos.

Si quieres saber más sobre el algoritmo K-Nearest Neighbors y cómo seleccionar un valor "k" óptimo, lee este tutorial sobre KNN.

Construye un modelo de clasificación en Python

Aquí tienes algunos fragmentos de código que puedes utilizar para construir un modelo de clasificación en Python utilizando la biblioteca Scikit-Learn:

1. Regresión logística

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()

2. K vecinos más cercanos

from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()

Modelos basados en árboles de machine learning

Los modelos basados en árboles son algoritmos supervisados de machine learning que construyen una estructura en forma de árbol para hacer predicciones. Pueden utilizarse tanto para problemas de clasificación como de regresión.

En esta sección, exploraremos dos de los modelos de machine learning basados en árboles más utilizados: los árboles de decisión y los bosques aleatorios.

Árboles de decisión

Un árbol de decisión es el algoritmo de machine learning basado en árboles más sencillo. Este modelo nos permite dividir continuamente el conjunto de datos en función de parámetros específicos hasta tomar una decisión final.

He aquí un ejemplo sencillo que demuestra cómo funciona el algoritmo del árbol de decisión:

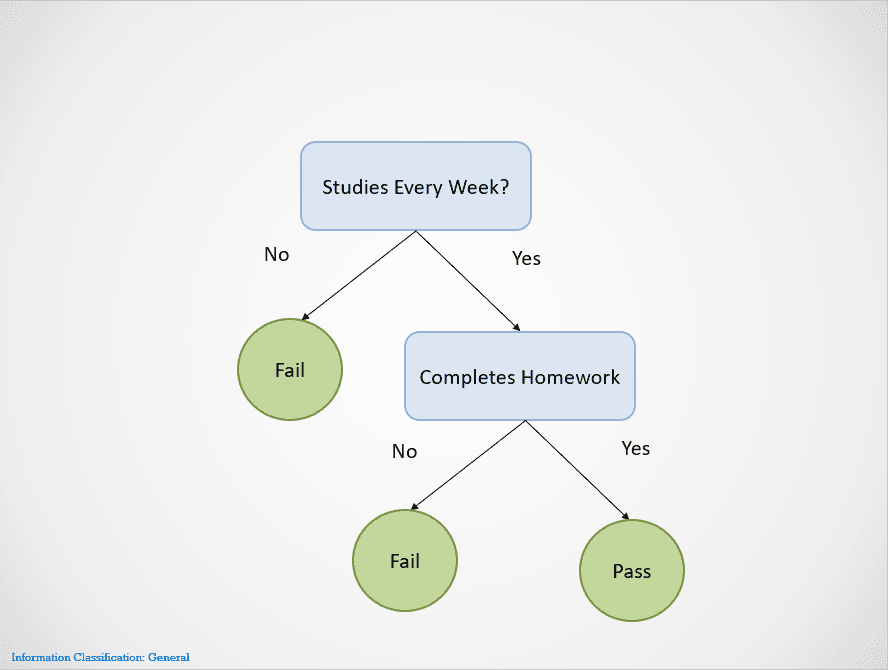
Imagen del autor

Los árboles de decisión se dividen en diferentes nodos hasta obtener un resultado. 

En este caso, si un alumno no estudia todas las semanas, suspenderá. Si estudian todas las semanas pero no completan los deberes, el resultado sigue siendo "Fail" (Suspenso). Sólo aprobarán si estudian todas las semanas y terminan todos los deberes.

Observa que el árbol de decisión anterior se divide primero en la variable "Studies Every Week?" (¿Estudias todas las semanas?) Entonces deja de dividir si la respuesta es "No", diciendo que el alumno suspenderá. 

El árbol de decisión elegirá primero una variable para dividir basándose en una métrica llamada entropía. Dejará de dividir cuando se obtenga una "división pura", es decir, cuando todos los puntos de datos pertenezcan a una única clase.

Hay muchas formas de construir un árbol de decisión. El árbol necesita encontrar una característica para dividirse en primera, segunda, tercera, etc. Esta estructura se crea a partir de una métrica llamada ganancia de información. El mejor árbol de decisión posible es el que tiene la mayor ganancia de información.

Para saber más sobre cómo funcionan los árboles de decisión, junto con métricas como la entropía y la ganancia de información, este artículo sobre la clasificación de árboles de decisión en Python tiene más detalles.

Una de las mayores ventajas de los árboles de decisión es que son muy interpretables. Es fácil trabajar hacia atrás y comprender cómo un árbol de decisión ha obtenido su resultado final basándose en el conjunto de datos de entrenamiento.

Sin embargo, los árboles de decisión también son muy propensos a sobreajustarse si se les deja crecer completamente. Esto se debe a que están diseñados para dividirse perfectamente en todas las muestras del conjunto de datos de entrenamiento, lo que hace que no puedan generalizar bien a datos externos.

Este inconveniente de los árboles de decisión puede resolverse utilizando el algoritmo del bosque aleatorio.

Bosques aleatorios

El modelo de bosque aleatorio es un algoritmo basado en árboles que nos ayuda a mitigar algunos de los problemas que surgen al utilizar árboles de decisión, uno de los cuales es el sobreajuste. Los bosques aleatorios se crean combinando las predicciones realizadas por múltiples modelos de árboles de decisión y devolviendo un único resultado.

Lo hace en dos pasos:

• Paso 1: en primer lugar, las filas y variables del conjunto de datos se muestrean aleatoriamente con reemplazamiento. A continuación, se crean múltiples árboles de decisión y se entrenan en cada muestra de datos. 
• Paso 2: a continuación, se combinan las predicciones realizadas por todos estos árboles de decisión para obtener un único resultado. Por ejemplo, si se entrenaran 3 árboles de decisión distintos y 2 de ellos predijeran "Yes" mientras que 1 predijera "No", entonces el resultado final del algoritmo del bosque aleatorio sería "Yes".

En el caso de un problema de regresión, el resultado será la predicción media de todos los árboles de decisión.

He aquí un sencillo ejemplo visual de cómo funciona el algoritmo de bosque aleatorio:

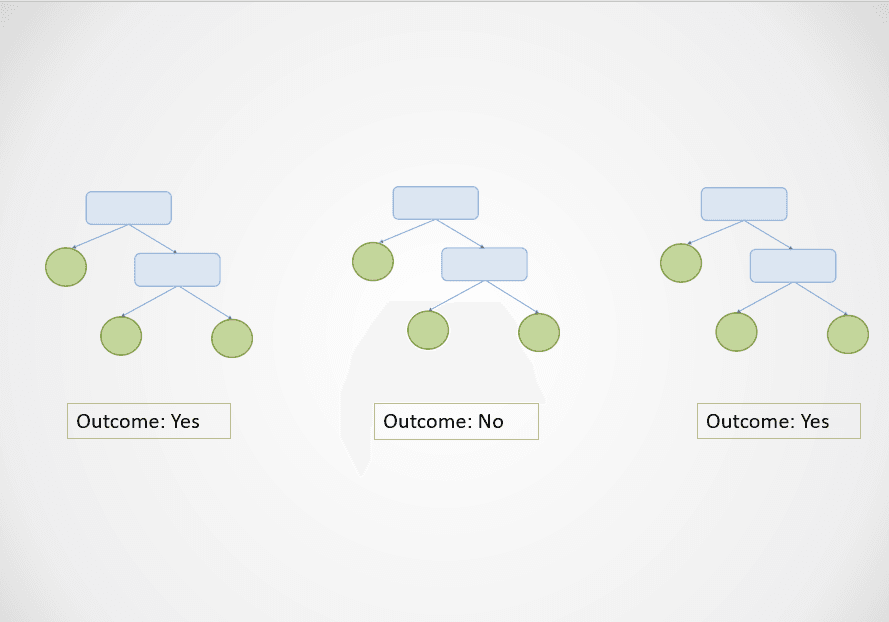
Imagen del autor

En el diagrama anterior, el primer y el tercer árbol de decisión predicen "Yes", mientras que el segundo predice "No".

Como se trata de una tarea de clasificación, se selecciona la clase mayoritaria. En este caso, el algoritmo del bosque aleatorio devolverá un resultado final de "Yes" basándose en las predicciones realizadas por 2 de los 3 árboles de decisión.

Una de las mayores ventajas del algoritmo del bosque aleatorio es que generaliza bien, ya que combina la salida de múltiples árboles de decisión entrenados en un subconjunto de características.

Además, mientras que el resultado de un único árbol de decisión puede variar drásticamente en función de un pequeño cambio en el conjunto de datos de entrenamiento, este problema no se plantea con el algoritmo de bosque aleatorio, ya que el conjunto de datos de entrenamiento se muestrea muchas veces.

Construye un modelo basado en árboles en Python

Ejecuta las siguientes líneas de código para construir un algoritmo de machine learning basado en árboles con Scikit-Learn:

1. Árbol de decisión 

# classification

from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()

# regression

from sklearn.tree import DecisionTreeRegressor
dt_reg = DecisionTreeRegressor()

2. Bosques aleatorios

# classification

from sklearn.ensemble import RandomForestClassifier
rf_clf = RandomForestClassifier()

# regression

from sklearn.ensemble import RandomForestRegressor
rf_reg = RandomForestRegressor()

Clustering de machine learning

Hasta ahora, hemos explorado modelos supervisados de machine learning para abordar problemas de clasificación y regresión. Ahora, nos sumergiremos en un popular enfoque de aprendizaje no supervisado llamado agrupación.

En palabras sencillas, la agrupación es la tarea de crear un grupo de objetos similares entre sí, pero diferentes de los demás. Esta técnica tiene diversos usos empresariales, como recomendar películas a usuarios con patrones de visionado similares en un sitio de streaming de vídeo, detección de anomalías y segmentación de clientes.

En esta sección, examinaremos un algoritmo llamado agrupación de K-Means, el modelo de machine learning más sencillo y popular utilizado para tareas de aprendizaje no supervisado.

Agrupación K-Means

La agrupación de K-Means es una técnica de machine learning no supervisada que se utiliza para agrupar objetos similares en los datos.

Aquí tienes un ejemplo de cómo funciona el algoritmo de agrupación K-Means:

Imagen del autor

Paso 1: la imagen anterior está formada por observaciones sin etiquetar que no se han agrupado. Inicialmente, cada observación se asignará a un conglomerado de forma aleatoria. A continuación, se calculará un centroide para cada conglomerado. 

Se representan con el símbolo "+" en el diagrama siguiente:

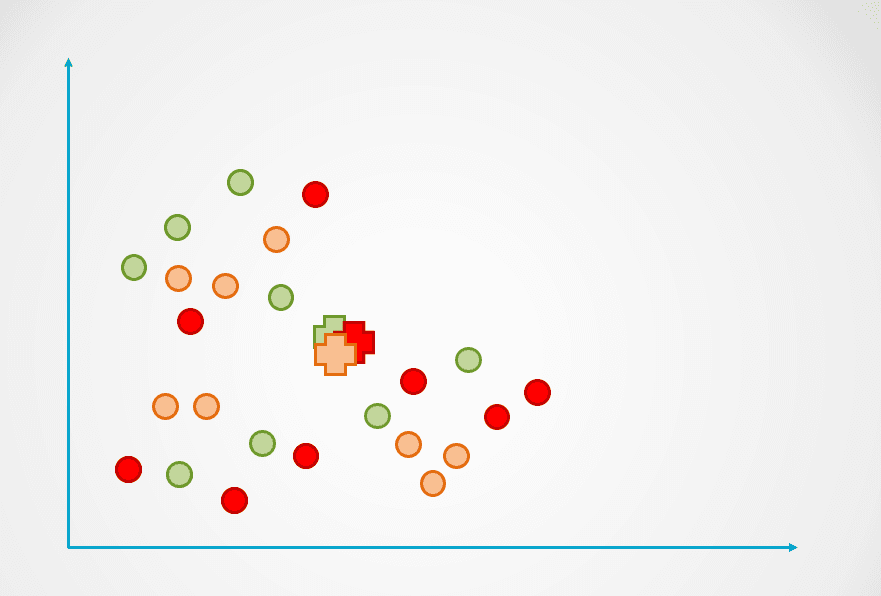
Imagen del autor

Paso 2: a continuación, se mide la distancia de cada punto de datos al centroide, y cada punto se asigna al centroide más cercano:

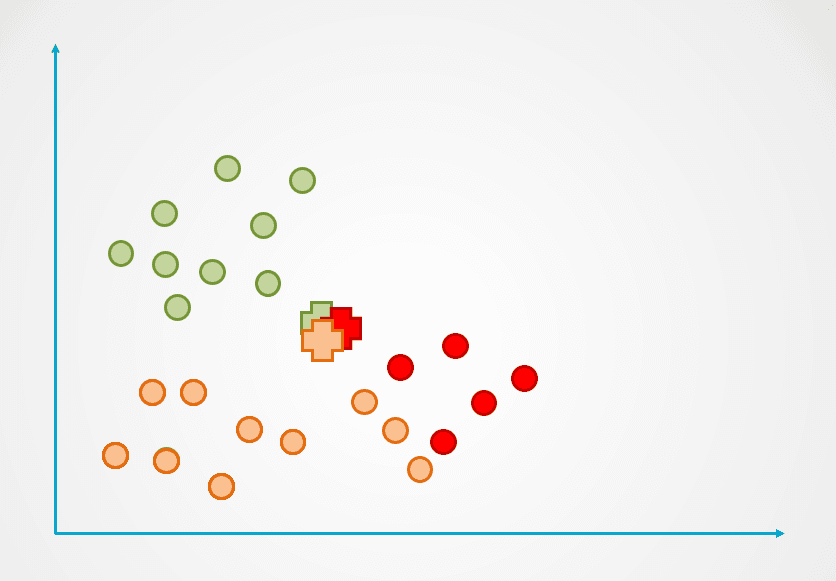
Imagen del autor

Paso 3: entonces se recalcula el centroide del nuevo conglomerado, y los puntos de datos se reasignarán en consecuencia.

Paso 4: este proceso se repite hasta que ya no se reasignan puntos de datos:

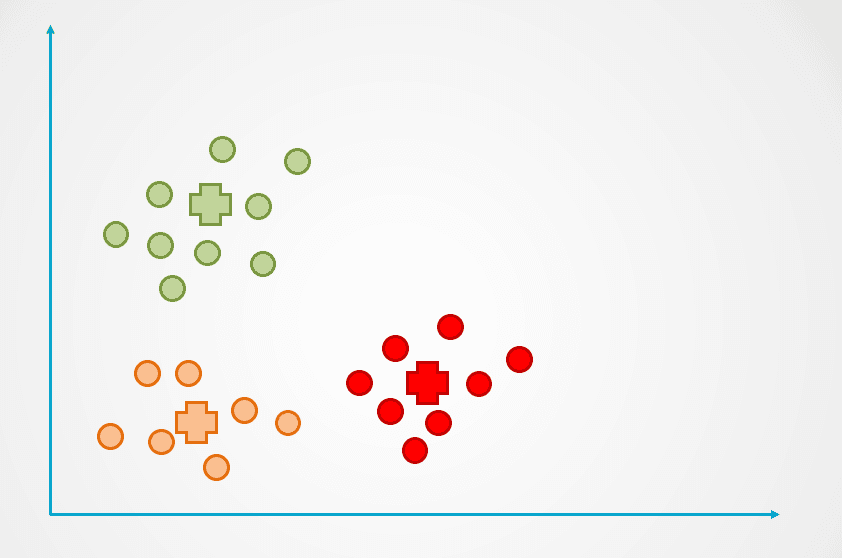
Imagen del autor

Observa que en el ejemplo anterior se crearon tres clusters o agrupaciones. El número de conglomerados se denomina "k" en el algoritmo de agrupación K-Means, y lo tenemos que determinar nosotros.

Hay algunas formas distintas de seleccionar "k" en K-Means, la más popular de las cuales es el método del codo. Esta técnica consiste en trazar el error para un número diferente de conglomerados en un gráfico y elegir el punto de inflexión de la curva como "k". 

Aprende más en nuestro tutorial de agrupación de K-Means en Python para descubrir el método del codo y el funcionamiento interno de la agrupación de K-Means.

Construye un modelo de agrupación K-Means en Python

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 3, init='k-means++')

El argumento n_clusters indica el número de clusters "k" que debes definir al construir el algoritmo.

Explicación de los modelos de machine learning - Próximos pasos:

Si has conseguido seguir todo este artículo, ¡enhorabuena! Ahora conoces algunos de los modelos y algoritmos de machine learning supervisados y no supervisados más populares y cómo pueden aplicarse para resolver diversos problemas de modelado predictivo.

Para convertirte en un científico de datos, necesitas comprender cómo funcionan los distintos tipos de modelos de machine learning para aplicarlos a la resolución de un problema. Por ejemplo, si quieres construir un modelo que sea interpretable y tenga un tiempo de cálculo bajo, puede tener sentido crear un árbol de decisión. Sin embargo, si tu objetivo es crear un modelo que generalice bien, puedes optar por construir un algoritmo de bosque aleatorio.

También es importante saber cómo evaluar los modelos de machine learning. Un "buen" modelo es subjetivo y depende en gran medida de tu caso de uso. En los problemas de clasificación, por ejemplo, una alta precisión por sí sola no es indicativa de un buen modelo. Como científico de datos, necesitas revisar métricas como la precisión, la exhaustividad y la puntuación F1 para hacerte una mejor idea de lo bien que está funcionando tu modelo.

Si quieres profundizar en los modelos de machine learning más allá de los conceptos tratados en este artículo, sigue el curso Científico de Machine Learning con Python. Este Programa de carrera te enseñará la teoría que hay detrás del funcionamiento de los modelos de machine learning y cómo se pueden implementar en Python. En el curso también aprenderás técnicas de preparación de datos como la normalización, la descorrelación y la selección de características.