Classification techniques are an essential part of machine learning and data mining applications. Approximately 70% of data science problems are classification problems. There are lots of classification problems available, but logistic regression is common and is a useful regression method for solving the binary classification problem. Another category of classification is Multinomial classification, which handles the issues where multiple classes are present in the target variable. For example, the IRIS dataset is a very famous example of multi-class classification. Other examples are classifying article/blog/document categories.
Logistic regression can be used for various classification problems, such as spam detection. Some other examples include: diabetes prediction, whether a given customer will purchase a particular product; whether or not a customer will churn, whether the user will click on a given advertisement link or not, and many more examples.
Logistic Regression is one of the most simple and commonly used Machine Learning algorithms for two-class classification. It is easy to implement and can be used as the baseline for any binary classification problem. Its basic fundamental concepts are also constructive in deep learning. Logistic regression describes and estimates the relationship between one dependent binary variable and independent variables.
To easily run all the example code in this tutorial yourself, you can create a DataLab workbook for free that has Python pre-installed and contains all code samples. For more practice on logistic regression, check out the exercises in our Credit Risk Modeling in R course, which has plenty of real-world examples.
What is Logistic Regression?
Logistic regression is a statistical method for predicting binary classes. The outcome or target variable is dichotomous in nature. Dichotomous means there are only two possible classes. For example, it can be used for cancer detection problems. It computes the probability of an event occurrence.
It is a special case of linear regression where the target variable is categorical in nature. It uses a log of odds as the dependent variable. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
Linear Regression Equation:
![]()
Where y is a dependent variable and x1, x2 ... and Xn are explanatory variables.
Sigmoid Function:
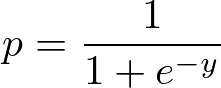
Apply Sigmoid function on linear regression:
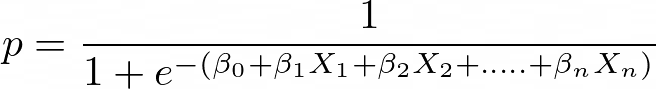
Properties of Logistic Regression:
- The dependent variable in logistic regression follows Bernoulli Distribution.
- Estimation is done through maximum likelihood.
- No R Square, Model fitness is calculated through Concordance, KS-Statistics.
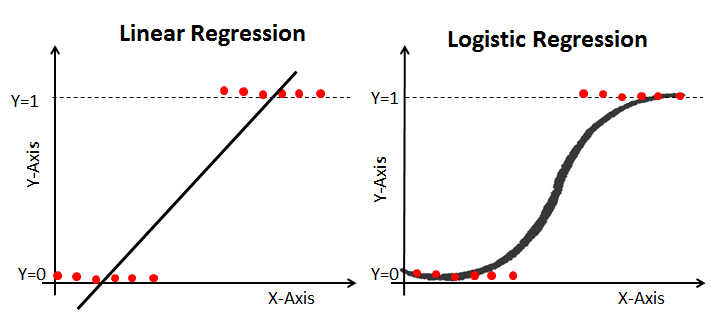
Linear Regression Vs. Logistic Regression
Linear regression gives you a continuous output, but logistic regression provides a constant output. An example of the continuous output is house price and stock price. Examples of the discrete output are predicting whether a patient has cancer or not and predicting whether a customer will churn. Logistic regression is estimated using the maximum likelihood estimation (MLE) approach, while linear regression is typically estimated using ordinary least squares (OLS), which can also be considered a special case of MLE when the errors in the model are normally distributed.
Maximum Likelihood Estimation Vs. Least Squares Method
The MLE is a "likelihood" maximization method, while OLS is a distance-minimizing approximation method. Maximizing the likelihood function determines the parameters that are most likely to produce the observed data. From a statistical point of view, MLE sets the mean and variance as parameters in determining the specific parametric values for a given model. This set of parameters can be used for predicting the data needed in a normal distribution.
Ordinary Least squares estimates are computed by fitting a regression line on given data points that has the minimum sum of the squared deviations (least square error). Both are used to estimate the parameters of a linear regression model. MLE assumes a joint probability mass function, while OLS doesn't require any stochastic assumptions for minimizing distance.
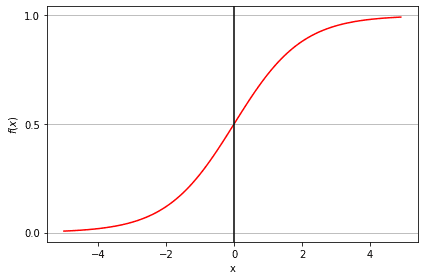
Sigmoid function
The sigmoid function, also called logistic function, gives an ‘S’ shaped curve that can take any real-valued number and map it into a value between 0 and 1. If the curve goes to positive infinity, y predicted will become 1, and if the curve goes to negative infinity, y predicted will become 0. If the output of the sigmoid function is more than 0.5, we can classify the outcome as 1 or YES, and if it is less than 0.5, we can classify it as 0 or NO. For example, if the output is 0.75, we can say in terms of the probability that there is a 75 percent chance that a patient will suffer from cancer.

Types of Logistic Regression
Types of Logistic Regression:
- Binary Logistic Regression: The target variable has only two possible outcomes such as Spam or Not Spam, Cancer or No Cancer.
- Multinomial Logistic Regression: The target variable has three or more nominal categories, such as predicting the type of Wine.
- Ordinal Logistic Regression: the target variable has three or more ordinal categories, such as restaurant or product rating from 1 to 5.
Model building in Scikit-learn
Let's build the diabetes prediction model using a logistic regression classifier.
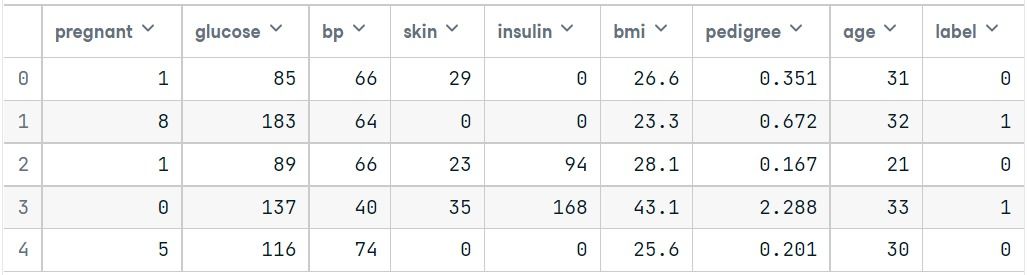
Let's first load the required Pima Indian Diabetes dataset using the pandas' read CSV function. You can download data from the following link: https://www.kaggle.com/uciml/pima-indians-diabetes-database or select a dataset from DataCamp: https://www.datacamp.com/datalab/datasets. The ready-to-use dataset provides you the option to train the model on DataLab, DataCamp's free Jupyter notebook on the cloud.
Loading data
We will simplify columns by providing col_names to pandas read_csv() function.
#import pandas
import pandas as pd
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
pima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()Selecting features
Here, you need to divide the given columns into two types of variables dependent(or target variable) and independent variable(or feature variables).
#split dataset in features and target variable
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableSplitting data
To understand model performance, dividing the dataset into a training set and a test set is a good strategy.
Let's split the dataset by using the function train_test_split(). You need to pass 3 parameters: features, target, and test_set size. Additionally, you can use random_state to select records randomly.
# split X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=16)Here, the Dataset is broken into two parts in a ratio of 75:25. It means 75% data will be used for model training and 25% for model testing.
Model development and prediction
First, import the LogisticRegression module and create a logistic regression classifier object using the LogisticRegression() function with random_state for reproducibility.
Then, fit your model on the train set using fit() and perform prediction on the test set using predict().
# import the class
from sklearn.linear_model import LogisticRegression
# instantiate the model (using the default parameters)
logreg = LogisticRegression(random_state=16)
# fit the model with data
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)Model Evaluation using Confusion Matrix
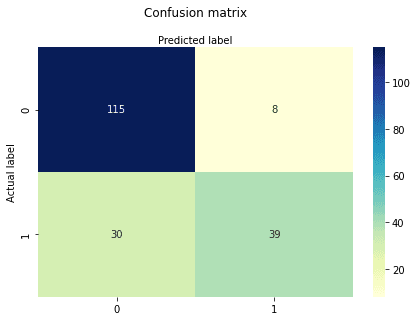
A confusion matrix is a table that is used to evaluate the performance of a classification model. You can also visualize the performance of an algorithm. The fundamental part of a confusion matrix is the number of correct and incorrect predictions summed up class-wise.
# import the metrics class
from sklearn import metrics
cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
cnf_matrixarray([[115, 8],
[ 30, 39]])Here, you can see the confusion matrix in the form of the array object. The dimension of this matrix is 2*2 because this model is binary classification. You have two classes 0 and 1. Diagonal values represent accurate predictions, while non-diagonal elements are inaccurate predictions. In the output, 115 and 39 are actual predictions, and 30 and 8 are incorrect predictions.
Visualizing confusion matrix using a heatmap
Let's visualize the results of the model in the form of a confusion matrix using matplotlib and seaborn.
Here, you will visualize the confusion matrix using Heatmap.
# import required modules
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
class_names=[0,1] # name of classes
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)
# create heatmap
sns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
Text(0.5,257.44,'Predicted label');Confusion matrix evaluation metrics
Let's evaluate the model using classification_report for accuracy, precision, and recall.
from sklearn.metrics import classification_report
target_names = ['without diabetes', 'with diabetes']
print(classification_report(y_test, y_pred, target_names=target_names)) precision recall f1-score support
without diabetes 0.79 0.93 0.86 123
with diabetes 0.83 0.57 0.67 69
accuracy 0.80 192
macro avg 0.81 0.75 0.77 192
weighted avg 0.81 0.80 0.79 192Well, you got a classification rate of 80%, considered as good accuracy.
Precision: Precision is about being precise, i.e., how accurate your model is. In other words, you can say, when a model makes a prediction, how often it is correct. In your prediction case, when your logistic regression model predicted patients are going to suffer from diabetes, that patients have 73% of the time.
Recall: If there are patients who have diabetes in the test set and your logistic regression model can identify it 57% of the time.
ROC curve
Receiver Operating Characteristic (ROC) curve is a plot of the true positive rate against the false positive rate. It shows the tradeoff between sensitivity and specificity.
y_pred_proba = logreg.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()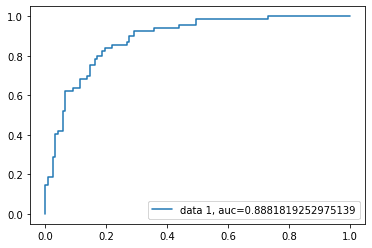
AUC score for the case is 0.88. AUC score 1 represents a perfect classifier, and 0.5 represents a worthless classifier.
The code source is available on DataLab: Understanding Logistic Regression in Python.
Advantages
Because of its efficient and straightforward nature, it doesn't require high computation power, is easy to implement, easily interpretable, and used widely by data analysts and scientists. Also, it doesn't require scaling of features. Logistic regression provides a probability score for observations.
Disadvantages
Logistic regression is not able to handle a large number of categorical features/variables. It is vulnerable to overfitting. Also, it can't solve the non-linear problems, which is why it requires a transformation of non-linear features. Logistic regression will not perform well with independent variables that are not correlated to the target variable and are very similar or correlated to each other.
Conclusion
In this tutorial, you covered a lot of details about logistic regression. You have learned what logistic regression is, how to build respective models, how to visualize results and some of the theoretical background information. Also, you covered some basic concepts such as the sigmoid function, maximum likelihood, confusion matrix, ROC curve.
Hopefully, you can now utilize the Logistic Regression technique to analyze your own datasets. Thanks for reading this tutorial!
If you would like to learn more about Logistic Regression, take DataCamp's Machine Learning with scikit-learn course. You can also start your journey of becoming a machine learning engineer by signing up for Machine Learning Scientist with Python career track.