Exponentes en Python: Guía completa para principiantes

La exponenciación es fundamental en diversas áreas de la programación, del análisis de datos al diseño de algoritmos. Entre sus aplicaciones se incluyen el análisis de patrones exponenciales en grandes conjuntos de datos como las tendencias de las redes sociales y la realización de cálculos matemáticos como el interés compuesto o los tipos de interés.

Además, la exponenciación desempeña un papel crucial en el machine learning (ML) y la inteligencia artificial (IA), especialmente en redes neuronales y reconocimiento de imágenes. Por lo tanto, comprender cómo realizar cálculos con exponentes de forma eficaz en Python es esencial.

En esta guía exploraremos diferentes métodos para realizar la exponenciación en Python. Examinaremos las funciones integradas, las funciones del módulo matemático y las de la biblioteca Numpy. Cada método tiene sus ventajas.

Además, nos adentraremos en un caso práctico para comprender mejor los usos de la exponenciación.

Exponentes en Python

Python ofrece varias formas de calcular exponentes:

• **: El operador doble asterisco (**) es la opción más sencilla y básica para la exponenciación. Por ejemplo, x ** y calcula x elevado a y.
• pow(): Esta función integrada usa dos argumentos: la base y el exponente. Devuelve el resultado de elevar la base al exponente. También permite un tercer argumento opcional para la exponenciación modular. Ejemplo: pow(x, y).
• math.pow(): Esta función del módulo math es similar a pow(), pero siempre devuelve un resultado de coma flotante. Usa dos argumentos, que pueden ser flotantes o enteros. Ejemplo: math.pow(x, y).
• math.exp(): Otra función del módulo math, que devuelve la exponencial natural de un número, es decir, e elevado a la potencia del argumento. Ejemplo: math.exp(argument).
• np.power(): Esta función de la biblioteca NumPy está diseñada para trabajar con matrices. Realiza la exponenciación elemento por elemento. Ejemplo: np.power(array, exponent).

Conceptos básicos de exponentes en Python

El operador doble asterisco (**) es la forma más sencilla que tiene Python de calcular la exponenciación. Este operador eleva el operando izquierdo (base) a la potencia del operando derecho (exponente). También se llama operador potencia u operador exponente.

Si quieres mejorar tus conocimientos de programación en Python y aprender a programar como un auténtico programador, consulta el curso Programación en Python.

Exponente positivo

En este fragmento de código, mostramos cómo calcular la exponenciación utilizando exponentes positivos. Por ejemplo, 2 elevado a 3 se calcula como 2 × 2 × 2, que es 8. Del mismo modo, -10 elevado a 4 se calcula como -10 × -10 × -10 × -10, que es 10 000.

base = 2
exponent = 3
print(base**exponent)  # Output: 8

base = -10
exponent = 4
print(base**exponent)  # Output: 10000

Exponente negativo

Este código calcula el resultado de elevar una base a un exponente negativo. Por ejemplo, 5 elevado a -2 es igual a 0,04. Del mismo modo, 25 elevado a -5 es un valor muy pequeño representado en notación científica (1,024e-07).

base = 5
exponent = -2
print(base**exponent) # 0.04

base = 25
exponent = -5
print(base**exponent) # 1.024e-07

Elevar un número a un exponente negativo equivale a tomar el recíproco del número elevado al exponente positivo.

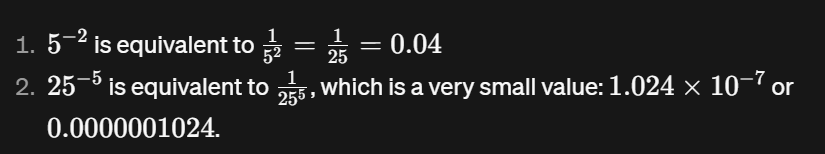
En Python, el operador ** devuelve ZeroDivisionError si elevas 0,0 a una potencia negativa, porque cualquier número dividido entre cero es indefinido.

base = 0
exponent = -5
print(base**exponent)

La salida es:

Exponente de coma flotante

Los ejemplos de código muestran que Python calcula correctamente el resultado de elevar una base positiva como 2 a un exponente fraccionario como 1,5. Sin embargo, utilizar una base negativa con un exponente fraccionario da como resultado un número complejo.

base = 2
exponent = 1.5
print(base**exponent) # 2.8284271247461903

base = -0.25
exponent = 1.25
print(base**exponent) # (-0.12500000000000003-0.125j)

Profundiza: Funciones integradas

Python proporciona diferentes funciones integradas para calcular exponentes, pero nos centraremos en dos: pow() y math.pow(). A primera vista, estas funciones pueden parecer similares, pero tienen algunas diferencias significativas. Profundicemos en cada función.

pow()

La función pow() usa dos argumentos obligatorios: base y exponente. Opcionalmente, pow() acepta un tercer argumento para calcular el módulo del valor exponencial. La sintaxis es la siguiente: pow(base, exp, mod), donde "mod" representa el módulo. Esta función devuelve el resto de la exponenciación.

Exponenciación básica

Para cálculos básicos, basta con proporcionar la base y el exponente a la función, que funciona de forma similar al operador **.

r = pow(2, 3)
print(r) # 8

r = pow(4, -10)
print(r) # 2.56e-06

Exponenciación de coma flotante

En el código siguiente, utilizamos números de coma flotante tanto para las bases como para los exponentes, algunos de los cuales son negativos. Este enfoque funciona de forma similar al operador **.

r = pow(3.5, 2)
print(r)  # 12.25

r = pow(3.5, -2)
print(r)  # 0.08163265306122448

r = pow(3.5, 3.2)
print(r)  # 55.08301986166747

r = pow(-3.5, -3.3)
print(r)  # (-0.009414432347757688+0.012957854474952653j)

r = pow(-3.5, 3.3)
print(r)  # (-36.698070584660925-50.510560868902246j)

Nota: Si se trata de exponenciación básica sin necesidad de cálculos modulares, el operador ** es una solución más concisa y legible que la función pow().

Exponenciación modular

El parámetro de módulo opcional de la función pow() es muy valioso cuando se trabaja con exponenciación modular. Esto es especialmente útil en criptografía o al tratar con números grandes, ya que la exponenciación modular ofrece una mayor eficiencia. Por ejemplo, al calcular 3 elevado a 4 módulo 5, el resultado es 1, ya que 81 módulo 5 es igual a 1.

r = pow(3, 4, 5)
print(r)  # 1

r = pow(123, 456, 789)
print(r)  # 699

r = pow(2, -3, 7)
print(r)  # 1

r = pow(-13, 8, 62)
print(r)  # 7

Quizá te preguntes por qué utilizar pow() directamente para la exponenciación modular es más eficiente que pow(base, exp) % mod o (base**exp) % mod. La función pow() integrada está diseñada específicamente para esta operación, mientras que los demás métodos realizan cálculos intermedios innecesarios. Esto puede suponer una diferencia significativa en el rendimiento, especialmente con valores grandes.

import timeit

start_pow_mod = timeit.default_timer()
pow(500000000, 3000, 4000)
stop_pow_mod = timeit.default_timer()

pow_mod_time = stop_pow_mod - start_pow_mod

print("Time using pow(base, exp, mod): ", pow_mod_time)

start_pow_other = timeit.default_timer()
pow(500000000, 3000) % 4000
stop_pow_other = timeit.default_timer()

pow_other_time = stop_pow_other - start_pow_other

print("Time using pow(base, exp) % mod:", pow_other_time)


start_aestrisk = timeit.default_timer()
(500000000**3000) % 4000
stop_aestrisk = timeit.default_timer()

aestrisk_time = stop_aestrisk - start_aestrisk

print("Time using (base ** exp) % mod: ", aestrisk_time)


print(
    f"Speed comparison: pow(base, exp, mod) was {pow_other_time / pow_mod_time} times faster than pow(base, exp) % mod and {aestrisk_time/pow_mod_time} times faster than (base ** exp) % mod"
)

La salida es:

La función pow() puede provocar diferentes errores dependiendo de la situación.

# Trying to take the modulo of complex numbers raises a ValueError.
print(pow(2 + 3j, 4, 5))  # ValueError: complex modulo

# Taking the third argument is not allowed if the second argument is negative.
print(pow(10, -11, 4))  # ValueError: base is not invertible for the given modulus

# If the first or second argument is a float, the third argument is not allowed.
print(pow(2.4, 3, 4))  # TypeError: pow() 3rd argument not allowed unless all arguments are integers

# Passing any argument as a string results in a TypeError.
print(pow(2, 4, '3'))  # TypeError: unsupported operand type(s) for pow(): 'int', 'int', 'str'

math.pow()

La función math.pow(x, n) eleva x a n. math.pow() convierte los argumentos en flotantes y devuelve el resultado como exponenciación precisa de coma flotante. Esta precisión resulta crucial en campos como el análisis de datos y la computación científica, donde la exactitud es primordial.

Este es el código sencillo. La función math.pow() devuelve un valor de coma flotante, mientras que la función pow() devuelve un valor entero.

import math
print(math.pow(6, 3))  # 216.0
print(pow(6, 3))  # 216

La función math.pow() no acepta números imaginarios.

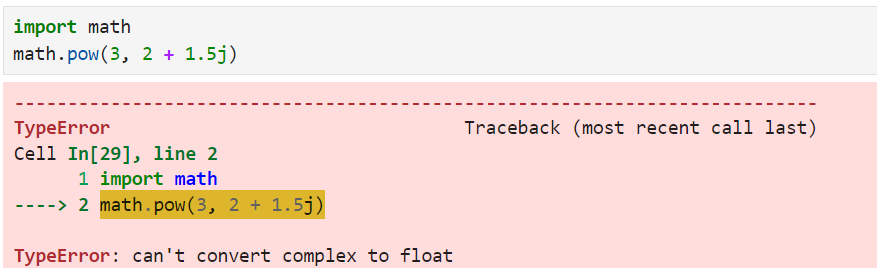
math.pow() no acepta bases negativas con exponentes fraccionarios, ya que aparecerá ValueError.

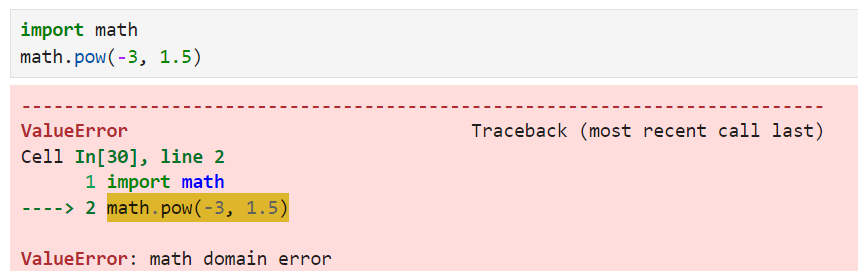
Aprovechar las bibliotecas para la exponenciación avanzada

Para manejar tareas de exponenciación avanzada, como hallar el valor exponencial de un número o calcular la exponenciación elemento por elemento en matrices, puedes aprovechar dos funciones: np.power() y math.exp().

np.power()

En Python, la exponenciación no se limita a las funciones integradas. Python dispone de una potente biblioteca llamada NumPy, que permite una gran variedad de operaciones matemáticas con matrices. A veces, debes usar exponenciación en matrices enteras, y aquí es donde entra np.power(). Se ha diseñado para la exponenciación elemento por elemento en matrices.

import numpy as np
r = np.power([2, 4, 8], 2)
print(r)  # [4, 16, 64]

r = np.power([2, 4, 8], [1, 2, 3])
print(r)  # [4 64 4096]

r = np.power([[2, 3, 4], [5, 6, 7]], [1, 2, 3])
print(r) # [[2 9 64] [5 36 343]]

La función np.power() no acepta un exponente negativo.

import numpy as np
r = np.power([2, 4, 8], -2)
print(r)

La salida es:

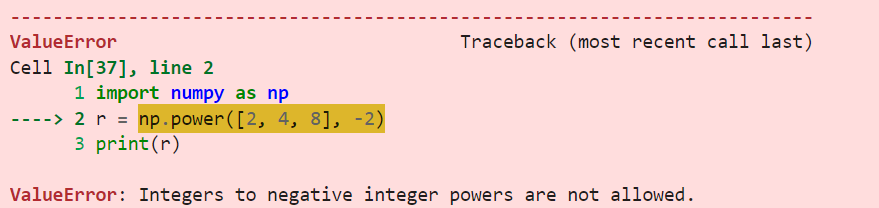
Si intentas elevar un número negativo a una potencia no entera, NumPy devolverá un valor NaN (no un número).

math.exp()

La función math.exp(x) calcula el valor exponencial de x, que equivale a elevar el número e e a x. El número e es aproximadamente igual a 2,71828, y en notación matemática esta operación se representa como e^x.

import math
x = 2
r = math.exp(x)
print("Exponential of", x, ":", r) # 7.38905609893065

Una característica importante de math.exp(x) es su adaptabilidad. Puede manejar números positivos, negativos e incluso números de coma flotante.

import math
print(math.exp(-2))  # 0.1353352832366127
print(math.exp(-2.5))  # 0.0820849986238988
print(math.exp(2.5))  # 12.182493960703473

Aplicaciones prácticas y ejemplos

La exponenciación es una operación fundamental en matemáticas con numerosas aplicaciones en el análisis de datos y la computación científica.

Si quieres dominar los fundamentos del análisis de datos con Python, consulta el curso Introducción a Python para la ciencia de datos.

Supongamos que tienes un archivo CSV que contiene datos sobre principal, tipo de interés y periodo de inversión para varias filas. Puedes calcular el interés compuesto de cada fila utilizando cualquiera de los métodos comentados anteriormente.

Principal,Rate,Years
1000,0.05,5
2000,0.03,10
1500,0.08,3
3000,0.06,7
2500,0.04,9
1800,0.07,4
2200,0.025,6
3500,0.09,2
2800,0.035,8
4000,0.02,5

Aquí tienes el código:

import csv


def compound_interest(principal, rate, years):
    return principal * (1 + rate) ** years


# Read data from CSV file

data = []
with open("data.csv", newline="") as csvfile:
    reader = csv.DictReader(csvfile)
    for row in reader:
        row["Compound Interest"] = compound_interest(
            float(row["Principal"]), float(row["Rate"]), int(row["Years"])
        )
        data.append(row)
# Write data to a new CSV file with compound interest column

output_file = "data.csv"
fieldnames = ["Principal", "Rate", "Years", "Compound Interest"]

with open(output_file, mode="w", newline="") as csvfile:
    writer = csv.DictWriter(csvfile, fieldnames=fieldnames)
    writer.writeheader()
    for row in data:
        writer.writerow(row)
print("Compound interest calculations saved to", output_file)

El resultado es:

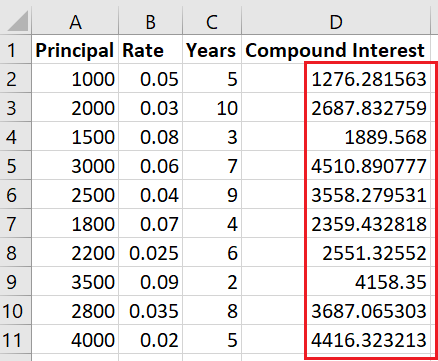
¡Estupendo! Has calculado el interés compuesto de todas las filas y lo has almacenado en una columna aparte. Puedes utilizar estos datos para análisis posteriores. Del mismo modo, hay cientos de otros casos de uso en los que se utiliza mucho la exponenciación, como el modelado del crecimiento de la población a lo largo del tiempo.

Conclusión

En esta guía, hemos explorado cinco métodos diferentes para calcular exponentes en Python, cada uno de los cuales ofrece ventajas únicas. Puedes utilizarlos para muchas situaciones prácticas, como hallar el interés compuesto, modelar el crecimiento de la población y mucho más.

Operador doble asterisco (**): Sencillo y directo para el uso diario.

pow(): Versátil con un truco opcional de "módulo".

math.pow(): Resultados precisos como números de coma flotante.

np.power(): Potente para manejar matrices con comprobación de errores.

math.exp(): Herramienta dedicada para calcular el valor exponencial.

Si quieres desarrollar tus habilidades estadísticas y aprender a recopilar, analizar y extraer conclusiones exactas de los datos utilizando Python, consulta el curso Introducción a la estadística en Python.