Introducción a k-Means Clustering con scikit-learn en Python

Introducción

En este tutorial, usted aprenderá acerca de k-means clustering. Cubriremos:

• Funcionamiento del algoritmo de agrupación k-means
• Cómo visualizar los datos para determinar si son buenos candidatos para la agrupación en clusters
• Estudio de entrenamiento y ajuste de un modelo de agrupación k-means a partir de un conjunto de datos reales sobre viviendas en California. 

Tenga en cuenta que esto no debe confundirse con k-próximos más cercanos, y los lectores que lo deseen deben ir a k-Nearest Neighbors (KNN) Classification with scikit-learn in Python en su lugar.

Es útil saberlo, ya que k-means clustering es un algoritmo de clustering muy popular que hace un buen trabajo agrupando datos esféricos en grupos distintos. Esto es muy valioso como herramienta de análisis cuando las agrupaciones de filas de datos no están claras o como paso de ingeniería de características para mejorar los modelos de aprendizaje supervisado. 

Esperamos una comprensión básica de Python y la capacidad de trabajar con pandas Dataframes para este tutorial.  

Visión general de la agrupación K-Means

Los modelos de clustering pretenden agrupar los datos en "clusters" o grupos distintos. Esto puede servir tanto como un punto de vista interesante en un análisis, o puede servir como una característica en un algoritmo de aprendizaje supervisado. 

Imaginemos un entorno social en el que grupos de personas discuten en diferentes círculos alrededor de una sala. Cuando miras la sala por primera vez, sólo ves un grupo de personas. Mentalmente podrías empezar a colocar puntos en el centro de cada grupo de personas y nombrar ese punto como un identificador único. De este modo, podrá referirse a cada grupo con un nombre único para describirlos. Esto es esencialmente lo que hace la agrupación k-means con los datos. 

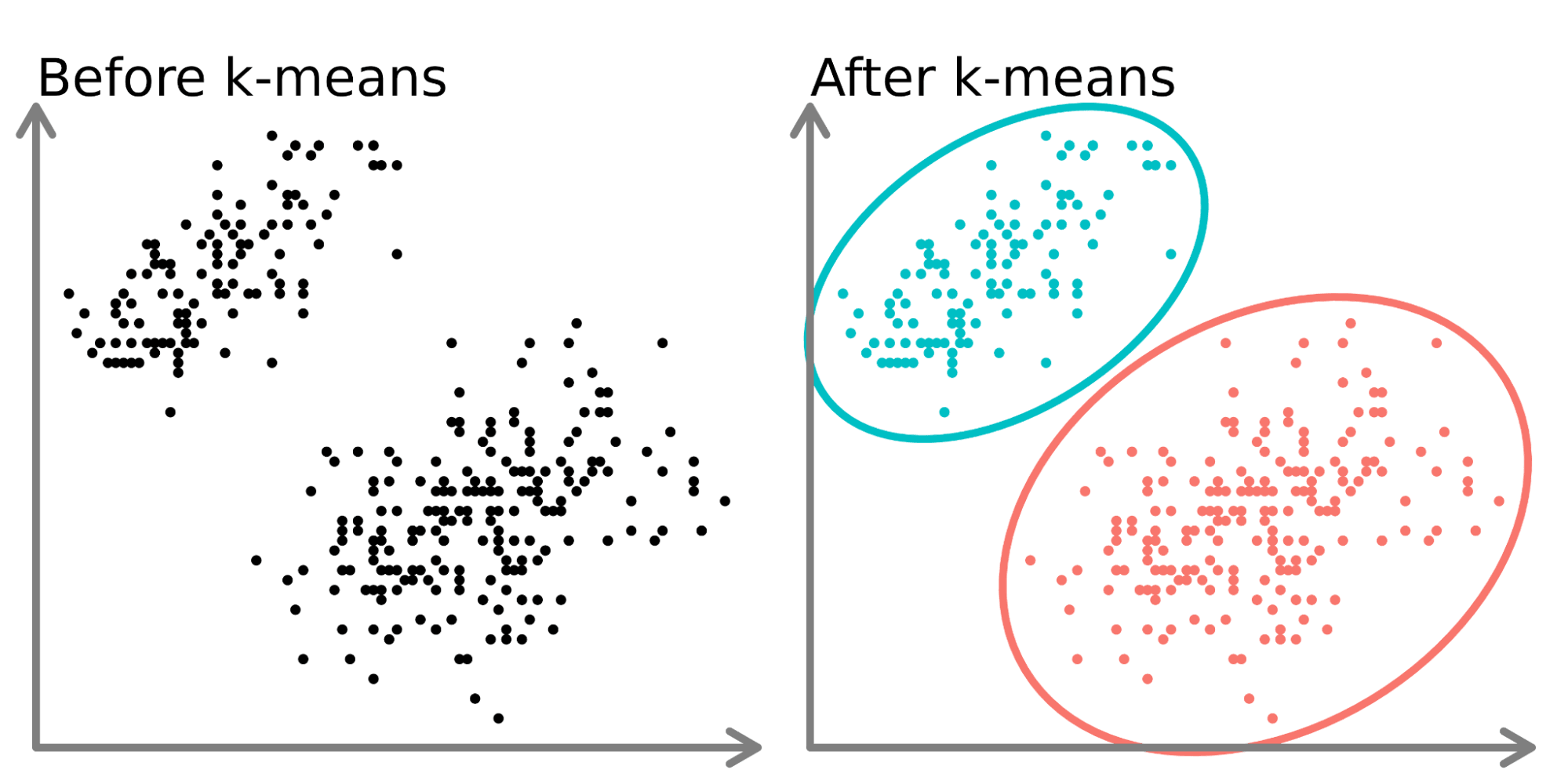
En la parte izquierda del diagrama anterior, podemos ver 2 conjuntos distintos de puntos sin etiquetar y coloreados como puntos de datos similares. El ajuste de un modelo k-means a estos datos (lado derecho) puede revelar 2 grupos distintos (mostrados en círculos y colores distintos). 

En dos dimensiones, es fácil para los humanos dividir estos conglomerados, pero con más dimensiones, es necesario utilizar un modelo.

El conjunto de datos

En este tutorial, utilizaremos los datos de viviendas de California de Kaggle(aquí). Utilizaremos datos de localización (latitud y longitud), así como el valor medio de la vivienda. Agruparemos las casas por localidades y observaremos cómo fluctúan los precios de la vivienda en California. Guardamos el conjunto de datos como un archivo csv llamado ‘housing.csv’ en nuestro directorio de trabajo y lo leemos utilizando pandas.

import pandas as pd

home_data = pd.read_csv('housing.csv', usecols = ['longitude', 'latitude', 'median_house_value'])
home_data.head()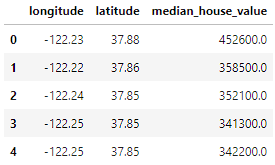

Los datos incluyen 3 variables que hemos seleccionado utilizando el parámetro usecols:

• longitud: Valor que representa la distancia a la que se encuentra una casa. Los valores más altos representan casas que están más al Oeste.
• latitud: Valor que representa la distancia al norte de una casa. Los valores más altos representan casas que están más al norte.
• median_house_value: El precio medio de la vivienda dentro de una manzana medido en USD. 

Flujo de trabajo de k-Means Clustering

Como otros algoritmos de Aprendizaje Automático, k-Means Clustering tiene un flujo de trabajo (ver A Beginner's Guide to The Machine Learning Workflow para un desglose más profundo del flujo de trabajo del Aprendizaje Automático).

En este tutorial, nos centraremos en la recopilación y división de los datos (en la preparación de datos) y en el ajuste de hiperparámetros, el entrenamiento del modelo y la evaluación del rendimiento del modelo (en el modelado). Gran parte del trabajo que conllevan los algoritmos de aprendizaje no supervisado consiste en ajustar los hiperparámetros y evaluar el rendimiento para obtener los mejores resultados del modelo.

Visualizar los datos

Empezamos visualizando nuestros datos de vivienda. Observamos los datos de localización con un mapa de calor basado en el precio medio de una manzana. Usaremos Seaborn para crear rápidamente gráficos en este tutorial (vea nuestro curso Introducción a la Visualización de Datos con Seaborn para entender mejor cómo se crean estos gráficos).

import seaborn as sns

sns.scatterplot(data = home_data, x = 'longitude', y = 'latitude', hue = 'median_house_value')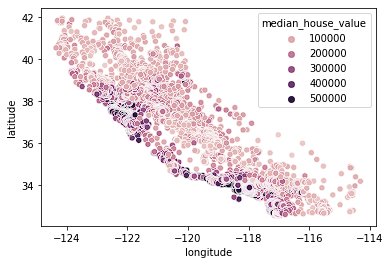

Vemos que la mayoría de las casas caras están en la costa oeste de California, con diferentes zonas que tienen grupos de casas de precio moderado. Esto es de esperar, ya que normalmente las propiedades situadas frente al mar valen más que las casas que no están en la costa. 

Las agrupaciones suelen ser fáciles de detectar cuando sólo se utilizan 2 ó 3 funciones. Se hace cada vez más difícil o imposible cuando el

Normalización de los datos

Cuando trabajamos con algoritmos basados en la distancia, como k-Means Clustering, debemos normalizar los datos. Si no normalizamos los datos, las variables con diferente escala se ponderarán de forma diferente en la fórmula de distancia que se está optimizando durante el entrenamiento. Por ejemplo, si incluyéramos el precio en el cluster, además de la latitud y la longitud, el precio tendría un impacto desproporcionado en las optimizaciones porque su escala es significativamente mayor y más amplia que las variables de localización acotadas. 

En primer lugar, configuramos las divisiones de entrenamiento y prueba utilizando train_test_split de sklearn. 

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(home_data[['latitude', 'longitude']], home_data[['median_house_value']], test_size=0.33, random_state=0)

A continuación, normalizamos los datos de entrenamiento y de prueba utilizando el método preprocessing.normalize() de sklearn. 

from sklearn import preprocessing

X_train_norm = preprocessing.normalize(X_train)
X_test_norm = preprocessing.normalize(X_test)

Ajuste y evaluación del modelo

Para la primera iteración, elegiremos arbitrariamente un número de conglomerados (denominado k) de 3. Construir y ajustar modelos en sklearn es muy sencillo. Crearemos una instancia de KMeans, definiremos el número de clusters utilizando el atributo n_clusters, estableceremos n_init, que define el número de iteraciones que el algoritmo ejecutará con diferentes semillas centroides, en "auto", y estableceremos random_state en 0 para obtener el mismo resultado cada vez que ejecutemos el código.  A continuación, podemos ajustar el modelo a los datos de entrenamiento normalizados utilizando el método fit().

from sklearn import KMeans

kmeans = KMeans(n_clusters = 3, random_state = 0, n_init='auto')
kmeans.fit(X_train_norm)

Una vez ajustados los datos, podemos acceder a las etiquetas desde el atributo labels_. A continuación, visualizamos los datos que acabamos de ajustar. 

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = kmeans.labels_)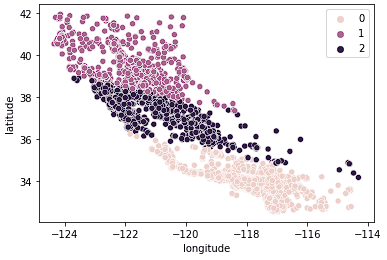

Vemos que los datos están ahora claramente divididos en 3 grupos distintos (Norte de California, Centro de California y Sur de California). También podemos observar la distribución de los precios medios de la vivienda en estos 3 grupos utilizando un diagrama de caja. 

sns.boxplot(x = kmeans.labels_, y = y_train['median_house_value'])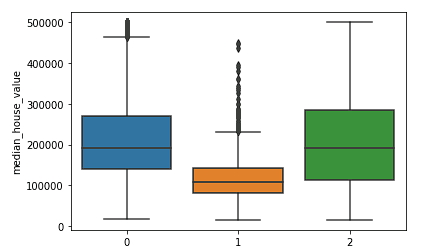

Vemos claramente que las agrupaciones del norte y del sur tienen distribuciones similares de valores medios de la vivienda (agrupaciones 0 y 2) que son superiores a los precios de la agrupación central (agrupación 1). 

Podemos evaluar el rendimiento del algoritmo de agrupación utilizando la puntuación Silhouette, que es una parte de sklearn.metrics en la que una puntuación más baja representa un mejor ajuste.

from sklearn.metrics import silhouette_score

silhouette_score(X_train_norm, kmeans.labels_, metric='euclidean')

Como no hemos analizado la fuerza de los distintos números de conglomerados, no sabemos hasta qué punto se ajusta bien el modelo k = 3. En la siguiente sección, exploraremos diferentes clusters y compararemos el rendimiento para tomar una decisión sobre los mejores valores de hiperparámetros para nuestro modelo.

Elegir el mejor número de clusters

El punto débil de la agrupación k-means es que no sabemos cuántos conglomerados necesitamos con sólo ejecutar el modelo. Tenemos que probar rangos de valores y tomar una decisión sobre el mejor valor de k. Normalmente tomamos una decisión utilizando el método del codo para determinar el número óptimo de conglomerados en el que no sobreajustamos los datos con demasiados conglomerados y tampoco los infraajustamos con muy pocos. 

Creamos el siguiente bucle para probar y almacenar los resultados de diferentes modelos, de forma que podamos tomar una decisión sobre el mejor número de clusters.

K = range(2, 8)
fits = []
score = []


for k in K:
    # train the model for current value of k on training data
    model = KMeans(n_clusters = k, random_state = 0, n_init='auto').fit(X_train_norm)
    
    # append the model to fits
    fits.append(model)
    
    # Append the silhouette score to scores
    score.append(silhouette_score(X_train_norm, model.labels_, metric='euclidean'))

A continuación, podemos examinar visualmente algunos valores diferentes de k. 

Primero examinamos k = 2.

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = fits[0].labels_)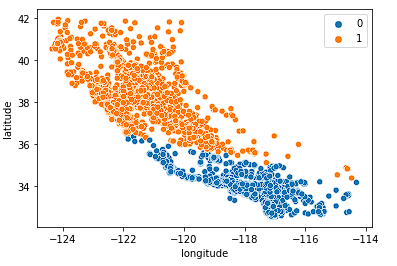

El modelo hace un buen trabajo al dividir el Estado en dos mitades, pero probablemente no capta suficientes matices del mercado inmobiliario californiano. 

A continuación, examinamos k = 4. 

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = fits[2].labels_)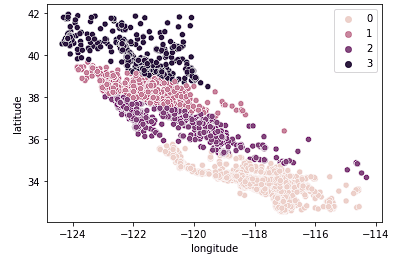

Vemos que este gráfico agrupa California en conjuntos más lógicos en todo el estado en función de lo al norte o al sur que se encuentren las casas en el estado. Lo más probable es que este modelo capte más matices del mercado de la vivienda a medida que nos desplazamos por el Estado. 

Por último, examinamos k = 7.

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = fits[2].labels_)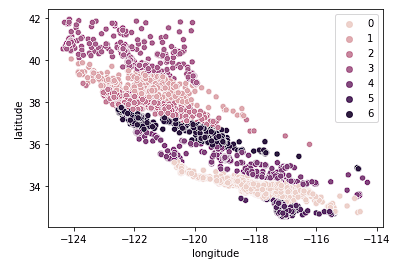

El gráfico anterior parece tener demasiados grupos. Hemos sacrificado la facilidad de interpretación de los conglomerados para obtener un resultado de geoagrupación "más preciso". 

Normalmente, a medida que aumentamos el valor de K, observamos mejoras en los conglomerados y en lo que representan hasta cierto punto. Entonces empezamos a ver rendimientos decrecientes o incluso peores resultados. Podemos ver esto visualmente para ayudar a tomar una decisión sobre el valor de k utilizando un gráfico de codo donde el eje y es una medida de la bondad del ajuste y el eje x es el valor de k. 

sns.lineplot(x = K, y = score)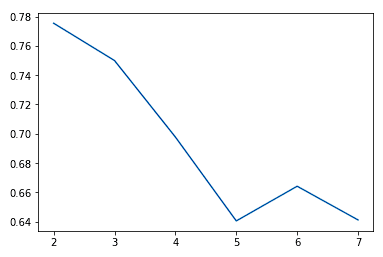

Solemos elegir el punto en el que las mejoras de rendimiento empiezan a aplanarse o a empeorar. Vemos que k = 5 es probablemente lo mejor que podemos hacer sin sobreajustar. 

También podemos ver que los clusters hacen un trabajo relativamente bueno al dividir California en distintos clusters y estos clusters se asignan relativamente bien a diferentes rangos de precios como se ve a continuación. 

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = fits[3].labels_)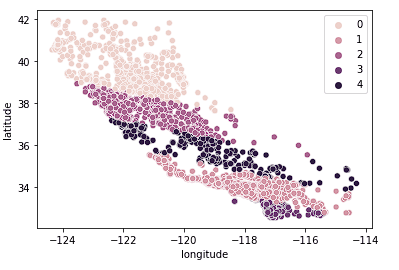

sns.boxplot(x = fits[3].labels_, y = y_train['median_house_value'])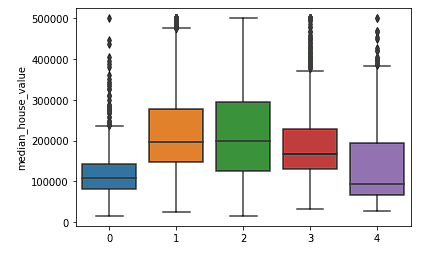

¿Cuándo fallará el análisis de conglomerados k-means?

La agrupación de K-means funciona mejor con datos esféricos. Los datos esféricos son datos que se agrupan en el espacio muy cerca unos de otros. Esto puede visualizarse más fácilmente en un espacio bidimensional o tridimensional. Los datos que no son esféricos o que no deberían serlo no funcionan bien con la agrupación k-means. Por ejemplo, la agrupación k-means no funcionaría bien con los datos siguientes, ya que no podríamos encontrar centros distintos para agrupar los dos círculos o arcos de forma diferente, a pesar de que visualmente son claramente dos círculos y arcos distintos que deberían etiquetarse como tales. 

Fuente de la imagen 

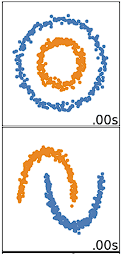
Hay muchos otros algoritmos de clustering que hacen un buen trabajo de clustering de datos no esféricos, cubiertos en Clustering in Machine Learning: 5 Algoritmos esenciales de clustering.

¿Debería dividir sus datos en conjuntos de entrenamiento y de prueba?

La decisión de dividir los datos depende de los objetivos de la agrupación. Si el objetivo es agrupar los datos al final del análisis, no es necesario. Si está utilizando los clusters como una característica en un modelo de aprendizaje supervisado o para predicción (como hacemos en el Tutorial Scikit-Learn: Baseball Analytics Pt 1 tutorial), entonces necesitará dividir sus datos antes de agruparlos para asegurarse de que está siguiendo las mejores prácticas para el flujo de trabajo de aprendizaje supervisado. 

Pase al siguiente nivel

Ahora que hemos cubierto los fundamentos del clustering k-means en Python, puedes consultar este curso de Aprendizaje no supervisado en Python para una buena introducción a k-means y otros algoritmos de aprendizaje no supervisado. Nuestro curso más avanzado, Análisis de conglomerados en Python, ofrece una visión más profunda de los algoritmos de conglomerados y de cómo construirlos y ajustarlos en Python. Por último, también puede consultar el tutorial An Introduction to Hierarchical Clustering in Python como un enfoque que utiliza un algoritmo alternativo para crear jerarquías a partir de datos.