Función NORM.DIST() en Excel: Calcular probabilidades y alturas de curvas

Si a menudo trabajas con probabilidades y estadísticas en Excel, es probable que tarde o temprano te encuentres con la función « NORM.DIST() ». Esta herramienta esencial es imprescindible para cualquiera que analice distribuciones normales, ya sea para realizar controles de calidad, evaluar resultados de exámenes o profundizar en datos empresariales. Con NORM.DIST(), puedes determinar fácilmente la probabilidad asociada a un valor específico dentro de una distribución normal.

En esta guía, comenzaremos por comprender qué hace realmente NORM.DIST(), luego desglosaremos su sintaxis, aclararemos opciones importantes y veremos ejemplos prácticos. Al final, sabrás exactamente cómo utilizar esta función y dónde encaja en tu kit de herramientas de Excel.

¿Qué hace NORM.DIST() en Excel?

Antes de entrar en detalles sobre cómo utilizar NORM.DIST(), aclaremos su finalidad. NORM.DIST() calcula la probabilidad de que un valor extraído de una distribución normal sea menor o igual a un número especificado. Según tus necesidades, puedes utilizarlo para obtener la densidad de probabilidad (la altura de la curva en un punto específico) o la probabilidad acumulada hasta ese valor.

Por lo tanto, tanto si deseas saber qué probabilidad hay de obtener una puntuación inferior a un número determinado, como si simplemente necesitas el valor de la curva normal en un punto, esta función te será de gran utilidad. A continuación, veamos qué incluye la función y cómo puedes configurarla en tu hoja de cálculo.

Sintaxis y argumentos de NORM.DIST() en Excel

Ahora que ya sabes más o menos qué hace NORM.DIST(), veamos cómo utilizarlo en Excel. Esta es la sintaxis de la función:

=NORM.DIST(x, mean, standard_dev, cumulative)

Analizando cada argumento:

• x: El valor para el que deseas la distribución.

• mean: La media (promedio) de la distribución.

• standard_dev: La desviación estándar de la distribución.

• cumulative: Un valor lógico: utiliza « TRUE » si deseas la función de distribución acumulativa (CDF) o « FALSE » si deseas la función de densidad de probabilidad (PDF).

Para poner esto en contexto, imagina que quieres encontrar la probabilidad de que un valor sea menor o igual a 80 en una distribución normal con una media de 70 y una desviación estándar de 10. La fórmula quedaría así:

=NORM.DIST(80, 70, 10, TRUE)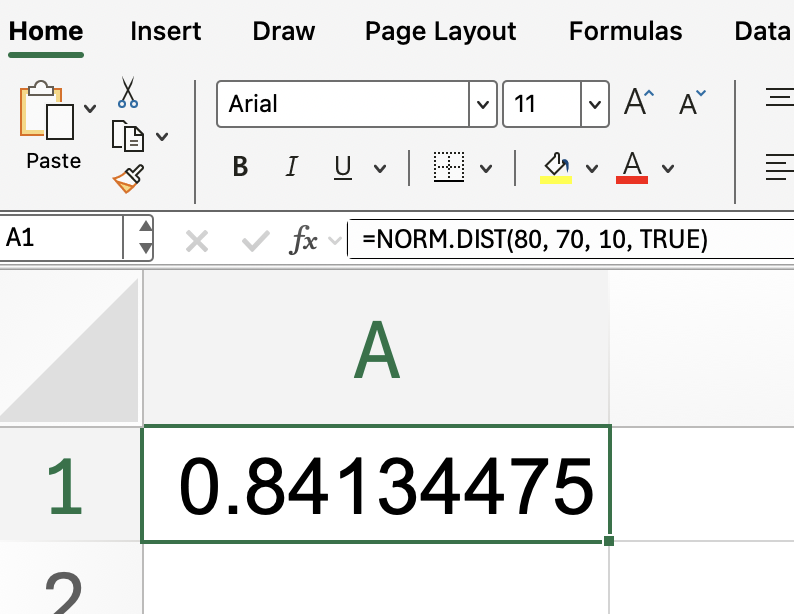

Esta configuración devuelve la probabilidad acumulada hasta 80. 

Acumulativo frente a Densidad de probabilidad en Excel NORM.DIST()

Ahora que ya sabes cómo configurar la función, quizá te preguntes cuáles son las dos opciones principales para el argumento final: acumulativa y densidad de probabilidad. Comprender la diferencia es fundamental para obtener los resultados que deseas.

• Acumulativo (VERDADERO): Cuando estableces el último argumento en « TRUE », « NORM.DIST() » devuelve la probabilidad de que un valor sea menor o igual que x. Esta es la opción más habitual para el análisis estadístico, ya que responde a preguntas como «¿Qué porcentaje de alumnos obtuvo una puntuación igual o inferior a 85?».

• Densidad de probabilidad (FALSO): Cuando seleccionas « FALSE » (Curva normal), la función te da la altura de la curva normal en x. No se trata de una probabilidad, sino del valor de la curva en ese punto, lo cual resulta útil principalmente en modelos estadísticos o en la teoría de la probabilidad.

Saber cuándo utilizar cada opción te ayudará a interpretar correctamente el resultado de la función. A continuación, veamos ambas opciones en acción con ejemplos prácticos.

Ejemplos en Excel NORM.DIST()

Para consolidar estas ideas, veamos dos situaciones prácticas: una utilizando la probabilidad acumulativa y otra utilizando la densidad de probabilidad.

1. Encontrar la probabilidad acumulativa con NORM.DIST()

Recordemos nuestro ejemplo anterior. No está de más practicar otra vez. Supongamos que quieres saber la probabilidad de que algo como la puntuación de un examen sea menor o igual a 85, suponiendo que las puntuaciones de los exámenes se distribuyen normalmente con una media de 75 y una desviación estándar de 8:

=NORM.DIST(85, 75, 8, TRUE)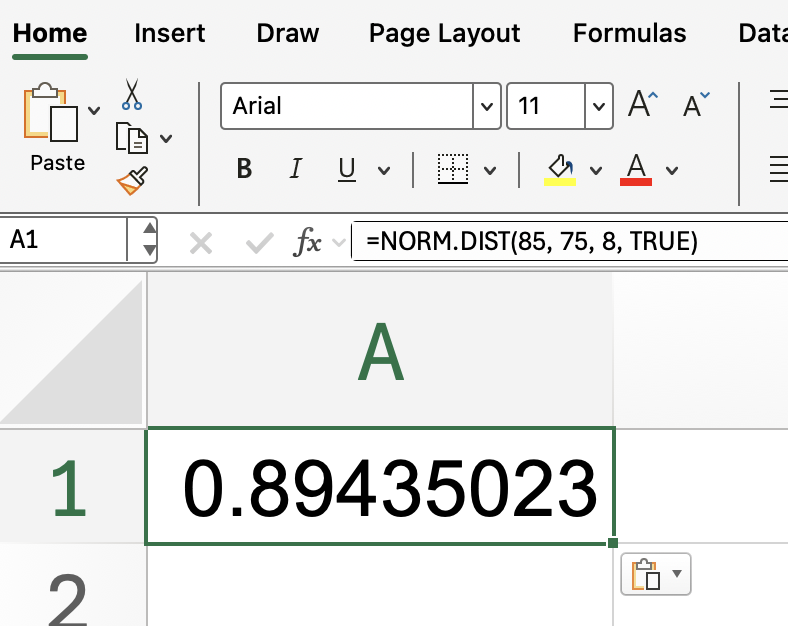

Excel devolverá un valor cercano a 0,894, lo que significa que aproximadamente el 89,4 % de los alumnos obtuvieron una puntuación igual o inferior a 85. Esta es una forma sencilla de evaluar la frecuencia con la que aparece una determinada puntuación en tus datos.

2. Obtener la densidad de probabilidad con NORM.DIST()

Pero, ¿qué pasa si te interesa la altura de la curva en un valor específico, en lugar de la probabilidad acumulativa? En ese caso, establece cumulative en FALSE:

=NORM.DIST(85, 75, 8, FALSE)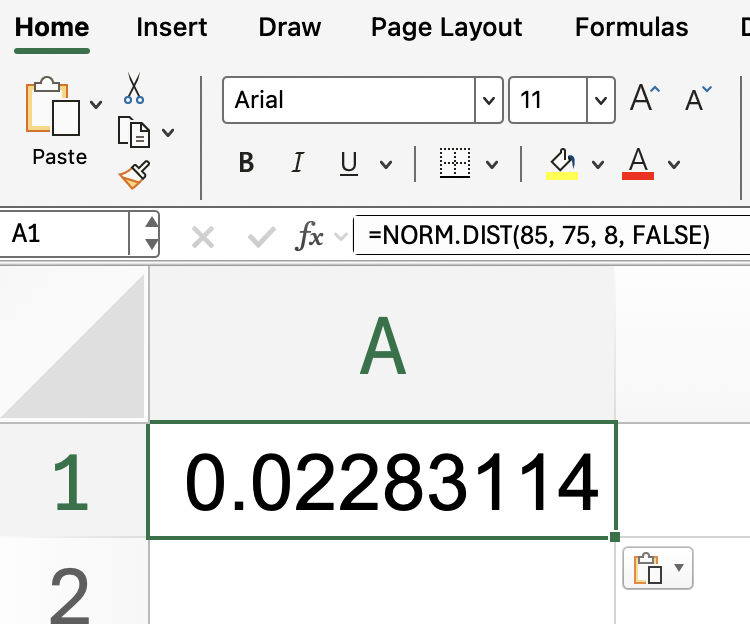

Esto te da la densidad de probabilidad en 85. Recuerda que no se trata de una probabilidad, sino del valor de la curva normal en ese punto.

Ahora ya sabes que NORM.DIST() se puede utilizar tanto para hallar la probabilidad acumulada para un valor dado como para hallar la altura de la curva en ese valor. Permítanme mostrarles una tabla final que resume estas ideas. 

La tabla siguiente ilustra cómo se comporta NORM.DIST() cuando se cambia entre los modos acumulativo y de densidad de probabilidad. Verás cómo los datos introducidos afectan al resultado y qué te indica realmente cada resultado.

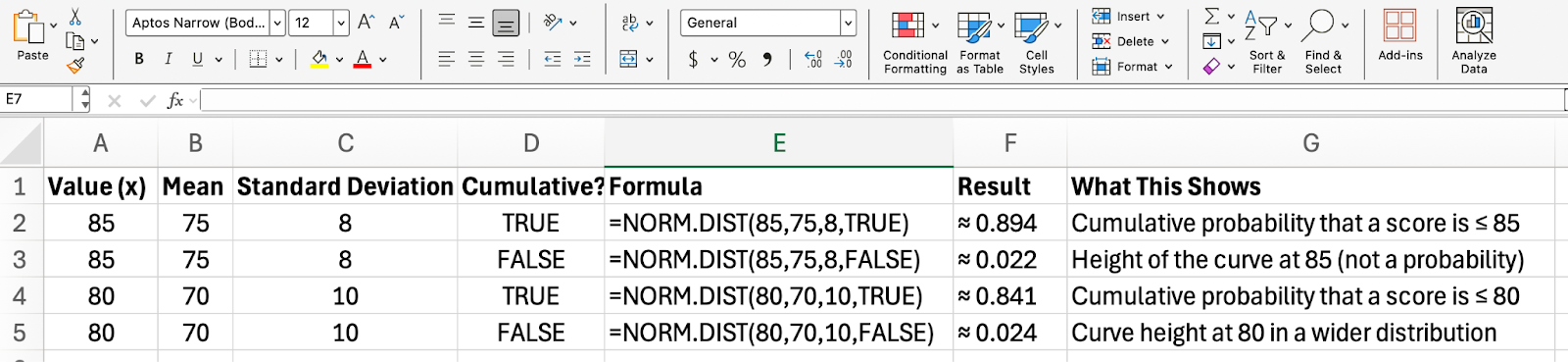
Problemas comunes y consejos para Excel NORM.DIST()

Cuando empieces a aplicar la optimización de datos ( NORM.DIST() ) a datos reales, es útil tener en cuenta algunos errores comunes:

• La desviación estándar debe ser positiva. Si introduces cero o un número negativo para la desviación estándar, se producirá un error.

• Flexibilidad media y desviación estándar. Mientras que la media puede ser cualquier número real, la desviación estándar siempre debe ser positiva, nunca cero ni negativa.

• ¿Vas marcha atrás? Si necesitas encontrar el valor correspondiente a una probabilidad dada (en lugar de la probabilidad para un valor dado), utiliza NORM.INV().

Si tienes en cuenta estos consejos, evitarás los errores más frecuentes y tus cálculos serán más precisos. A continuación, visualicemos cómo funciona el « NORM.DIST() » en una curva de campana para comprenderlo de forma más intuitiva.

Ejemplo visual en Excel NORM.DIST()

Ahora que has visto las fórmulas en acción, es útil visualizar lo que ocurre en segundo plano. Echa un vistazo a esta ilustración:

Introduce una tabla directamente en tu hoja de cálculo de Excel. En una nueva hoja o debajo de la tabla, crea tres columnas:

• Uno etiquetado con una x. En mi ejemplo, he establecido los valores del 60 al 90 en incrementos de 1.

• Uno para los valores acumulativos: =NORM.DIST(x_cell,75,8,TRUE)

• Uno para los Probabilidad : : =NORM.DIST(x_cell,75,8,FALSE)

A continuación, crea el gráfico:

• Resalta el x, Acumulativoy Probabilidad Densidad .
• Ve a Insertar > Gráficos > Gráfico de líneas o Dispersión con líneas suaves.

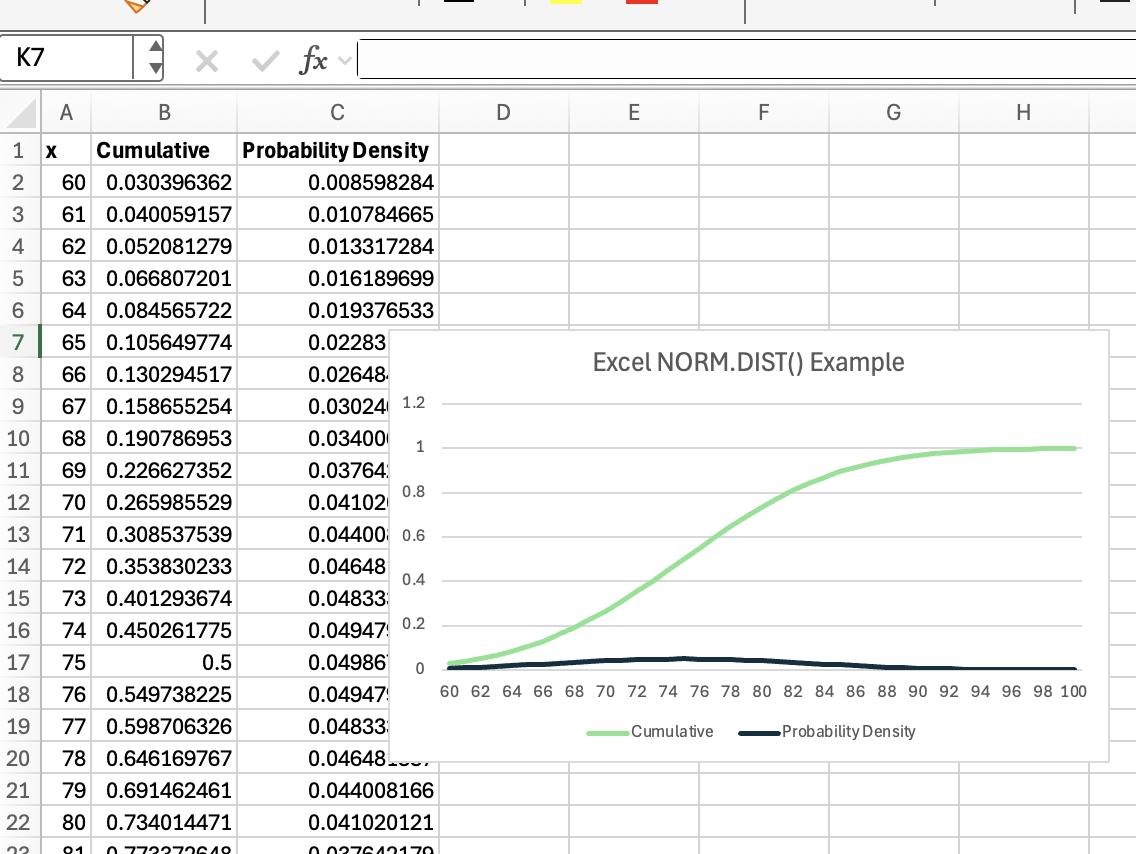
En esta curva de campana, el área sombreada bajo la curva hasta x representa la probabilidad acumulada que se obtiene al utilizar cumulative = TRUE. Mientras tanto, la altura de la curva en x muestra la densidad de probabilidad que se obtiene cuando cumulative = FALSE.

Funciones relacionadas en Excel

Hemos practicado NORM.DIST(), pero es posible que necesites herramientas relacionadas:

• NORM.INV(): Devuelve el valor correspondiente a una probabilidad acumulativa dada (la inversa de NORM.DIST()).

• NORM.S.DIST(): Calcula probabilidades utilizando la distribución normal estándar (media 0, desviación estándar 1).

• NORM.S.INV(): Devuelve el valor para una probabilidad dada i en una distribución normal estándar de n.

Estas funciones son especialmente útiles cuando se trabaja con datos estandarizados o cuando necesitas pasar de probabilidades a valores. Si estás abordando tareas estadísticas más complejas, considera explorar estas opciones relacionadas.

Conclusión

Ahora ya has visto cómo encaja la distribución de NORM.DIST() e en cualquier análisis de datos que implique la distribución normal. Tanto si estás calculando la probabilidad de que un valor caiga por debajo de un umbral determinado como si estás analizando la forma de la distribución, esta función hace que tu trabajo sea más preciso.

Como siguiente paso, realiza nuestrocurso Análisis de datos en Excel para seguir mejorando tus habilidades.