Curso
Puede que veas la curva de campana, que recibe muchos nombres, como la distribución normal o la distribución de Gauss, prácticamente en todas partes, sobre todo si tienes ojo para la estadística o la ciencia de datos. Parece pero no es un accidente de la naturaleza: Resulta que mucho de lo que medimos es el resultado de muchos pequeños factores sumados, lo que apunta a la presencia de un modelo aditivo subyacente. El teorema del límite central explica por qué: Cuando una variable está influida por muchos factores pequeños e independientes, la suma de estas variables tiende a seguir una distribución normal, independientemente de las distribuciones originales de las que procedan.
Transformando cualquier distribución normal en una forma especial llamada distribución normal estándar, podemos tomar la presencia de este modelo aditivo e ir un paso más allá normalizando esta distribución para hacerla aún más útil en contextos específicos. Exploraremos cómo se utiliza la distribución normal estándar para calcular probabilidades, hacer inferencias estadísticas y aplicar pruebas estadísticas utilizando propiedades bien establecidas de la distribución. Al final de este artículo, tendrás claro qué es la distribución normal estándar, por qué damos el paso adicional de estandarizarla y cómo se relaciona todo esto con la variabilidad, la probabilidad y la comprobación de hipótesis. Al final, espero que también te inscribas en nuestro curso de Introducción a la Estadística en R o en nuestro curso de Inferencia Estadística en R para seguir profundizando en las ideas de este artículo.
¿Qué es la Distribución Normal Estándar?
La distribución normal estándar es una forma específica de la distribución normal en la que la media es cero y la desviación típica es uno. También debemos decir que la distribución es simétrica y que las probabilidades de ciertos valores disminuyen simétricamente a medida que te alejas del centro.

"Distribución Normal Estándar" Imagen de Dall-E
Comprender las ecuaciones de la distribución normal estándar
Profundicemos un poco más en los aspectos matemáticos de la distribución normal estándar.
La PDF de la distribución normal estándar
Si no estás familiarizado con la idea de función de densidad de probabilidad (FDP), debes saber que describe cómo se distribuyen las probabilidades entre los posibles valores de una variable aleatoria continua. Toda distribución de probabilidad continua, como la distribución exponencial, la distribución t o la distribución de Cauchy, tiene su propia función de densidad de probabilidad que define la curva. Aquí se define la PDF de la distribución normal estándar: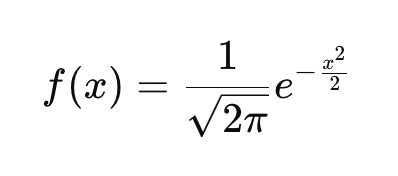
Esta función garantiza que el área bajo la curva se integre a 1. Si observas la ecuación e introduces distintos valores de x, obtendrás la altura de la curva en esos puntos. En la ecuación:
- x representa cualquier número real y es la variable de entrada de la función. Aparece en el exponente de la función, que es -x2/2. Controla la forma de la curva.
- Como x2 siempre es no negativo, y hay un signo negativo delante, el exponente siempre es negativo o cero.
- En el caso concreto en que x=0, el exponente es mayor, haciendo que f(x) alcance su máximo.
- Si x se aleja de 0 en sentido positivo o negativo, x2 aumenta, haciendo que el exponente sea más negativo. Unexponente más negativo da lugar a un valor menor de la función, lo que significa, junto con las otras cosas que hemos dicho, que la f(x) disminuye simétricamente a ambos lados de x=0.
- La base del exponente, que es el número de Euler, garantiza el rápido decaimiento de la función a medida que x se aleja de cero en cualquier dirección.
- La constante 1/√(2π) garantiza que el área total bajo la curva sea igual a 1.
La FCD de la distribución normal estándar
A diferencia de la FDP, que da la probabilidad relativa de distintos valores, la FCD te dice la probabilidad de que una variable sea menor o igual que un valor dado. Al igual que la FDP, toda distribución continua de probabilidad tiene su propia FDA.
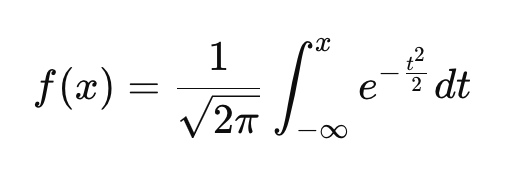
Esta ecuación es un poco más complicada, pero podemos resolverla:
- La integral significa que en lugar de dar la altura de la curva en x, la FCD nos dice la probabilidad total desde -∞ hasta x.
- Cuando x→-∞, la FCD se aproxima a 0.
- Cuando x=0 la FCD es 0,5ya que la distribución es simétrica y la mitad de la probabilidad está a la izquierda de cero.
- Como x→∞la FCD se aproxima a 1.
Por qué nos importa la distribución normal estándar
Nuestra guía sobre la distribución gaussiana tiene algunas buenas ideas sobre cuándo te conviene ajustar tus datos a una distribución normal. Pero a veces, puede que quieras cambiar tus datos a una normal estándar específicamente. He aquí algunas razones comunes:
La normal estándar se utiliza en las pruebas de hipótesis
Una distribución normal estándar hace que nuestros datos sean más comparables y utilizables con determinados métodos estadísticos. Al convertir los datos en puntuaciones Z, podemos comparar las observaciones de distintas distribuciones normales. En concreto, constituye la base de las pruebas Z, que utilizamos cuando queremos determinar si una media muestral difiere significativamente de una media poblacional.
En cambio, la prueba t utiliza la desviación típica de la muestra como estimación de la desviación típica de la población, por lo que se basa en la distribución t, que tiene colas más gruesas que la distribución normal estándar. Lee nuestro tutorial Prueba T vs. Z-test: Cuándo utilizar cada una, que habla de cosas como la varianza poblacional y muestral.
La normal estándar compara datos en una escala común
Como los distintos conjuntos de datos y variables pueden tener unidades y escalas diferentes, las comparaciones directas pueden ser difíciles. Pero cuando las conviertes en puntuaciones Z restando la media y dividiendo por la desviación típica, tienes una comparación fácil entre distintas distribuciones. Si se aplica a un conjunto de datos con distribución normal, se obtiene una distribución normal estándar . Por ejemplo, convertir las puntuaciones del SAT y del GRE, que supongo que se distribuyen normalmente, en puntuaciones Z nos permite comparar el rendimiento de los alumnos en relación con sus respectivas poblaciones de examen.
La norma normal se utiliza en el control de calidad
Se sabe que esta norma normal es importante para controlar la calidad del producto en la fabricación. Al examinar detenidamente las probabilidades, los fabricantes pueden determinar si las fluctuaciones de la calidad se deben a una variación aleatoria o a algún otro problema subyacente. Esto está relacionado con la prueba de hipótesis, que hemos mencionado antes, y también con una tabla de puntuación Z, de la que hablaremos más adelante.
La normal estándar se utiliza en la modelización estadística
La distribución normal estándar desempeña un papel en la evaluación de errores en modelos como la regresión lineal y la previsión de series temporales. En estos modelos, suponemos que los residuos, que son las diferencias entre los valores observados y los predichos, no sólo siguen una distribución normal, sino que también se pueden estandarizar para que sigan una distribución normal estándar.
En regresión lineal, los residuos normalizados son residuos que se han convertido en valores normalizados, lo que nos permite medir lo extremo que es un error en unidades de desviación típica, lo que puede facilitar la detección de valores atípicos. Esto es útil porque la heteroscedasticidad en los residuos, que puede no ser evidente en los predictores del modelo, puede distorsionar la interpretación de los residuos.
En el análisis de series temporales, se suele suponer que los errores de previsión siguen una distribución normal estándar cuando están debidamente normalizados. Esto es importante para construir intervalos de predicción. Muchos modelos de series temporales, como ARIMA, se basan en cuantiles normales estándar para definir límites de confianza en torno a las previsiones. También, en la descomposición de series temporales, el componente resto, que capta las fluctuaciones irregulares, suele tener una distribución normal. Si normalizas este componente resto, podrías hallar la probabilidad de valores extremos en tu serie temporal que sabes que no son resultado de la tendencia-ciclo o de la estacionalidad. Nuestro curso de Previsión en R te enseñará este tipo de técnicas.
La normal estándar se utiliza en el aprendizaje automático
Muchos algoritmos de aprendizaje automático funcionan mejor cuando los datos están a escala estándar. Estoy pensando en la regresión logística, la agrupación de k-means y las redes neuronales.
También estoy pensando en el análisis de componentes principales, que a menudo se utiliza como técnica de preprocesamiento. En el ACP, queremos que nuestras características de entrada tengan media cero y varianza unitaria para ayudar a a evitar que dominen las características con valores grandes. Un paso habitual del preprocesamiento es normalizar los datos restando la media y dividiéndola por la desviación típica. Esto garantiza que cada característica tenga media cero y varianza unitaria, pero debemos tener claro que esto no impone la normalidad. Sin embargo, en algunos casos, espero que los datos transformados se aproximen a la normalidad si la distribución original ya era cercana a la normalidad.
La normal estándar se utiliza para el cálculo de probabilidades
La función de distribución acumulativa de la distribución normal estándar, de la que hemos hablado antes, está bien tabulada, es decir, precalculada y organizada en tablas ampliamente disponibles, lo que facilita el cálculo de probabilidades porque basta con utilizar la tabla para buscar el valor correcto.
Por ejemplo, para hallar la probabilidad de que una altura elegida al azar esté por debajo de 1,80 m, estandarizamos la altura utilizando la distribución normal de la población y buscamos la puntuación Z en una tabla normal estándar. He puesto una versión de la tabla normalizada estándar al final de este artículo por si necesitas utilizarla.
Transformaciones para Alinear los Datos con la Distribución Normal Estándar
Las transformaciones pueden ayudar a remodelar los datos en una distribución normal estándar. A grandes rasgos, se trataría de un proceso en dos partes. En primer lugar, remodelaríamos nuestros datos para convertirlos en normales y, a continuación, realizaríamos la normalización de la puntuación Z.
Como nota, normalmente no aplicarías la normalización de la puntuación Z como primer paso porque los valores extremos pueden distorsionar la desviación típica, ya que la media y la desviación típica son sensibles a los valores atípicos. Además, algunas transformaciones requieren datos positivos. Si aplicas primero la normalización de la puntuación Z, los valores centrados en la media pueden incluir números negativos, lo que puede causar problemas en las transformaciones que sólo funcionan con valores positivos. Me refiero concretamente a los logaritmos. Así que es mejor ir en orden: paso 1, luego paso 2.
Paso 1: Transforma los datos para que sean normales
Algunas ideas de transformación que podrías utilizar son:
Transformación logarítmica para datos asimétricos
Cuando los datos están sesgados positivamente, una transformación logarítmica puede ayudar a normalizarlos. Por ejemplo, aplicar el logaritmo a los valores brutos comprime los valores grandes, reduciendo el sesgo y creando una distribución más simétrica.
Transformación de raíz cuadrada para datos de recuento
Para datos de recuento o conjuntos de datos moderadamente sesgados, podemos probar una transformación de raíz cuadrada. Este método reduce la variabilidad al tiempo que mantiene una estructura más simétrica, acercando los datos a la forma de la curva de campana.
Transformación Box-Cox para ajustes flexibles
La transformación Box-Cox va un paso más allá, adaptando la transformación a los datos. Su parámetro λ determina la fórmula exacta aplicada, lo que la hace muy versátil para ajustar los datos a las propiedades de la distribución normal estándar. Feature Engineering in R te mostrará el Box-Cox, entre otros muchos métodos importantes y útiles.
Paso 2: Realiza la normalización de las puntuaciones Z
Una vez aplicada una transformación, los datos pueden estandarizarse para ajustarse a la distribución normal estándar. Esto ajusta los datos para que tengan una media de cero y una desviación típica de uno. La fórmula de la puntuación Z es
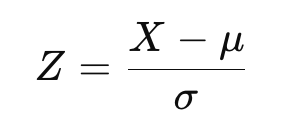
donde X son los datos transformados, μ es la media, y σ es la desviación típica.
Ahora bien, si estás familiarizado con la distinción entre puntuación Z poblacional y puntuación Z muestral, tal y como cubrimos en nuestro tema Inferencia Estadística en R, puede que reconozcas la ecuación anterior como la ecuación para una puntuación Z poblacional. Si trabajas con una muestra en lugar de con toda la población, estimaríamos en su lugar la media y la desviación típica:
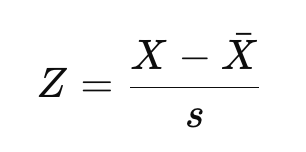
Aquí, X-bar es la media muestral, y s es la desviación típica muestral.
El resultado sería el mismo si utilizaras la media y la desviación típica del nuevo conjunto de datos normalizado. Pero a veces los investigadores pueden estar interesados en comparar los datos en relación con una población de referencia mayor, utilizando en su lugar algún tipo de media de referencia y desviación típica.
Imagina que observas un conjunto de datos sobre la renta, que estaría sesgado a la derecha, y haces una transformación logarítmica para normalizarlo. Imagina también que queremos comparar los ingresos en relación con los puntos de referencia nacionales, en cuyo caso utilizaríamos la media y la desviación típica nacionales en lugar de las de nuestra muestra para calcular las puntuaciones Z. El objetivo sería permitir una comparación significativa entre conjuntos de datos o estudios.
Así que, básicamente, si utilizas una muestra, técnicamente obtienes una aproximación normal estandarizada en lugar de la distribución normal estándar teórica exacta. Creo que es una distinción que merece la pena aclarar, aunque la diferencia deba ser pequeña para los grandes conjuntos de datos.
Visualización de la distribución normal estándar
He aquí una forma de crear una distribución normal estándar teórica en el lenguaje de programación R. En este código, también he añadido líneas verticales para las puntuaciones estándar, también conocidas como puntuaciones Z, que es una forma de decirnos, para cualquier valor dado, cuántas desviaciones estándar por encima o por debajo de la media de la población está nuestro valor .
install.packages("ggplot2")
library(ggplot2)
ggplot(data.frame(x = c(-4, 4)), aes(x)) +
stat_function(fun = dnorm, geom = "area", fill = '#ffe6b7', color = 'black', alpha = 0.5, args = list( mean = 0, sd = 1)) +
labs(title = "Standard Normal Distribution", subtitle = "Standard Deviations and Z-Scores") +
theme(plot.title = element_text(hjust = 0.5, face = "bold")) +
theme(plot.subtitle = element_text(hjust = 0.5)) +
geom_vline(xintercept = 1, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -1, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = 2, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -2, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = 3, linetype = 'dotdash', color = "black") +
geom_vline(xintercept = -3, linetype = 'dotdash', color = "black") +
geom_text(aes(x=1, label="\n 1 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=2, label="\n 2 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=3, label="\n 3 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-1, label="\n-1 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-2, label="\n-2 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11)) +
geom_text(aes(x=-3, label="\n-3 σ", y=0.125), colour="#376795", angle=90, text=element_text(size=11))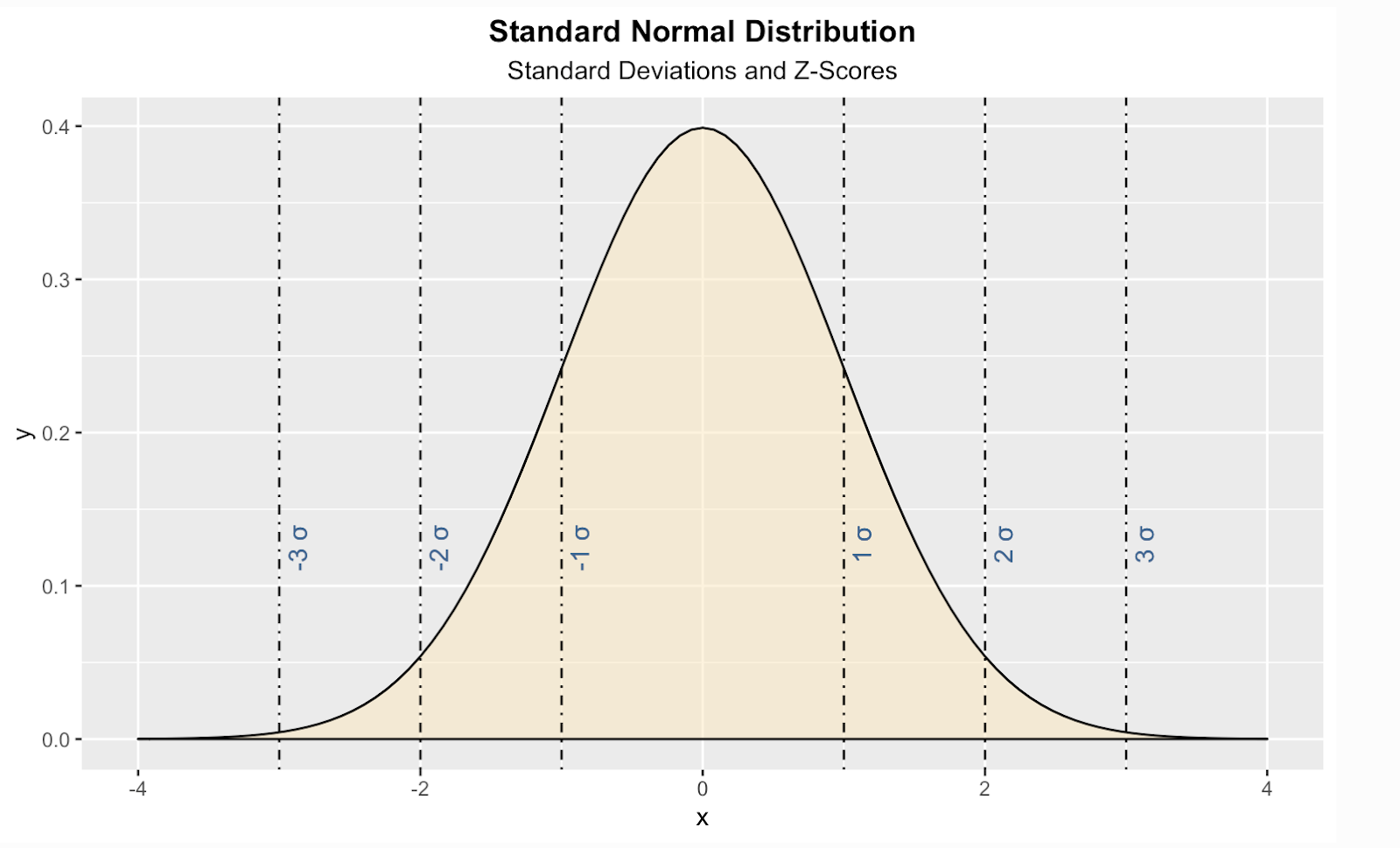
Debes saber que hay algunas distribuciones similares que pueden parecerse a la normal estándar pero no lo son:
| Distribución | Por qué no es normal |
|---|---|
| Distribución t | Colas ligeramente más pesadas, depende de los grados de libertad |
| Distribución logística | Colas ligeramente más pesadas de lo normal, forma diferente |
| Distribución de Laplace | Pico más agudo, colas más pesadas, decaimiento exponencial |
La distribución normal estándar y la tabla normal estándar
Ahora permíteme volver a algo que he mencionado antes: la idea de una tabla normal estándar, también llamada tabla de puntuación Z, o tabla Z, que se utiliza para hallar probabilidades acumuladas para una puntuación Z, que representa el número de desviaciones estándar que tiene un valor respecto a la media en una distribución normal estándar. Esta tabla se utiliza habitualmente en estadística para pruebas de hipótesis, intervalos de confianza y cálculos de probabilidad. La idea es que, en lugar de calcular las probabilidades manualmente, puedas consultar la tabla para determinar rápidamente la proporción de valores que caen por debajo de una puntuación Z determinada.
Hay que practicar un poco para leer la tabla, y a veces las tablas tienen un aspecto diferente entre sí. Aquí lo ves estructurado en un formato bidimensional. El objetivo es facilitar la búsqueda de probabilidades para las puntuaciones Z cuando se trabaja con decimales. En este caso, la columna de la izquierda contiene el número entero y el primer decimal de la puntuación Z. La fila superior representa el segundo decimal. Para hallar la probabilidad asociada a una puntuación Z concreta, localiza la fila correspondiente a la primera parte de la puntuación Z y, a continuación, busca la columna que coincida con el segundo decimal. El valor en la intersección de esta fila y columna es la probabilidad acumulada, es decir, la proporción de puntos de datos que caen por debajo de esa puntuación Z.
Lo mejor es mostrar un ejemplo: Por ejemplo, supongamos que calculas una puntuación Z de 0,32 para la nota de un examen de un alumno. Esto significa que la puntuación está 0,32 desviaciones típicas por encima de la media. Ahora, utilicemos la tabla Z para hallar la probabilidad de que un valor seleccionado al azar sea inferior a esta puntuación Z.
- Paso 1: Localiza la fila de 0,3.
- Paso 2: Localiza la columna para 0,02.
- Paso 3: Mira en la intersección de la fila de 0,3 y la columna de 0,02. El valor en esta posición es 0,6915.
La probabilidad acumulada para Z = 0,32 es 0,6554, lo que significa que el 65,54% de los valores de una distribución normal estándar están a menos de 0,32 desviaciones típicas por encima de la media. Si necesitas determinar la probabilidad de que un valor sea mayor que una puntuación Z dada, resta el valor de la tabla a 1 antes de hallar la fila y la columna.
| Z | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.5793 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 |
| 0.2 | 0.6179 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 |
| 0.3 | 0.6554 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 |
| 0.4 | 0.6915 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 |
| 0.5 | 0.7257 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 |
| 0.6 | 0.7580 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 |
| 0.7 | 0.7881 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 |
| 0.8 | 0.8159 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 |
| 0.9 | 0.8413 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 |
| 1.0 | 0.8643 | 0.8849 | 0.9032 | 0.9192 | 0.9332 | 0.9452 | 0.9554 | 0.9641 | 0.9713 |
Conclusión
Espero que hayas disfrutado con esta exploración de la distribución normal estándar. Sigue aprendiendo con nosotros aquí en DataCamp. He mencionado nuestro curso de Introducción a la Estadística en R y nuestra pista de habilidades de Inferencia Estadística en R. Pero si prefieres Python, nuestro curso de Pensamiento Estadístico en Python y nuestro curso de Diseño Experimental en Python son dos magníficas opciones.

Preguntas frecuentes sobre la distribución normal estándar
¿En qué se diferencia la distribución normal estándar de una distribución normal?
La distribución normal estándar es un caso específico de la distribución normal en el que la media es 0 y la desviación típica es 1. Esta normalización facilita el cálculo de probabilidades y las comparaciones entre conjuntos de datos.
¿Restar la media y dividir por la desviación típica crea una distribución normal estándar
Restar la media y dividir por la desviación típica transforma un conjunto de datos en una forma normalizada, pero no crea necesariamente una distribución normal estándar, a menos que los datos originales estuvieran distribuidos normalmente.
¿Qué relación hay entre la distribución normal estándar y el teorema del límite central?
El teorema del límite central afirma que la suma de muchas variables aleatorias independientes e idénticamente distribuidas tiende a seguir una distribución normal, que puede estandarizarse a la forma normal estándar.
¿Qué representa una puntuación Z en la distribución normal estándar?
Una puntuación Z nos dice cuántas desviaciones típicas hay entre un valor y la media. Una puntuación Z positiva significa que el valor está por encima de la media, mientras que una puntuación Z negativa significa que está por debajo.
¿Cómo se relaciona la distribución normal estándar con los intervalos de confianza?
Los intervalos de confianza utilizan puntuaciones Z para determinar rangos de probabilidad para estimar parámetros de población. Por ejemplo, un intervalo de confianza del 95% corresponde a puntuaciones Z de aproximadamente ±1,96.


