Prueba Chi-cuadrado en hojas de cálculo

Prueba Chi-cuadrado

La prueba chi-cuadrado es una prueba estadística que puede utilizarse para determinar qué frecuencias observadas son significativamente diferentes de las frecuencias esperadas o no en una o más categorías(Fuente). En la expresión matemática, es la relación entre los resultados/frecuencias observados experimentalmente (O) y los resultados esperados teóricamente (E) a partir de determinadas hipótesis, o se calcula dividiendo la desviación global de las frecuencias observadas y esperadas por las frecuencias esperadas.

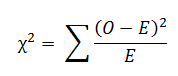
Si no hay diferencia entre las frecuencias observadas y las esperadas, entonces el valor de chi-cuadrado sería cero. Si existe una diferencia, entonces el valor de chi-cuadrado sería superior a cero.

Al comparar el valor calculado con los valores de la tabla, tienes que calcular el grado de libertad. Entonces podrás comparar y sacar una conclusión.

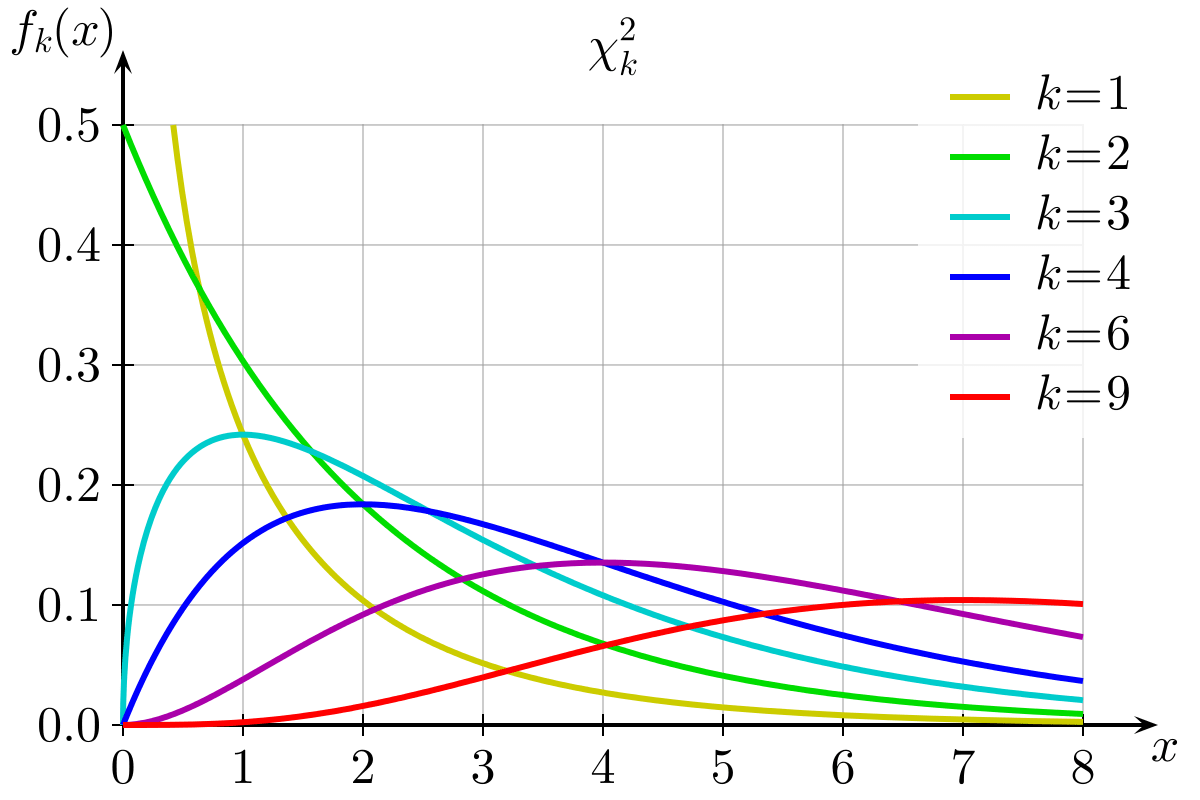
Gráfico de distribución de probabilidad chi-cuadrado: Fuente de la imagen:

Hay tres tipos de pruebas chi-cuadrado:

• Bondad de ajuste
• Prueba de independencia
• Prueba de homogeneidad

Terminología

• Tabla de contingencias: Se trata de una tabla cruzada o de dos direcciones. Sirve para mostrar una variable en una fila y otra en una columna con su recuento de frecuencias. Es un tipo de tabla de distribución de frecuencias de las variables categóricas.

• Frecuencias observadas: Son recuentos realizados a partir de datos experimentales. En otras palabras, observas los datos que se producen y realizas mediciones. (Fuente)

• Frecuencias previstas: Son recuentos calculados mediante la teoría de la probabilidad. Las frecuencias esperadas se calculan para cada celda de la tabla de contingencia.

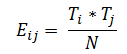
Dónde,

• Eij: Frecuencia esperada para la i-ésima fila y la j-ésima columna
• Ti: Total de la fila i
• Tj: Total de la fila j
• N: Total general

O puedes verlo como (total de filas * total de columnas) / total general

• Hipótesis nula (H0): Afirma que no existe asociación entre las dos variables cruzadas en la población. Por tanto, las variables son estadísticamente independientes. Por ejemplo, si comparas dos métodos A y B por su bondad o por cuál funciona mejor, y si la suposición es que ambos métodos son igual de buenos, entonces esta suposición se conoce como Hipótesis Nula.

• Hipótesis alternativa (HA): Propone que las dos variables estén relacionadas con la población. Si supones que de dos métodos, el método A es superior al método B o el método B es superior al método A, esta suposición se conoce como Hipótesis Alternativa.

• Grado de libertad: El número de variantes independientes que componen el estadístico se conoce como grado de libertad de ese estadístico.

Dónde,

• r=número de filas
• c=número de columnas

Se utilizará en la prueba de independencia y en la prueba de homogeneidad, no en la bondad del ajuste.

• Prueba de Chi-cuadrado Estadística: Un estadístico chi-cuadrado es un único número que te dice cuánta diferencia existe entre tus recuentos observados y los recuentos que esperarías si no hubiera ninguna relación en la población.
• Valor p de Chi-cuadrado: El valor P de Chi-cuadrado te dirá si los resultados de tu prueba son significativos o no.

Tipos de prueba Chi-cuadrado

1. Bondad de ajuste: La prueba de bondad de ajuste Chi-cuadrado es una prueba no paramétrica que se utiliza para averiguar en qué medida el valor observado de un fenómeno dado es significativamente diferente del valor esperado. En esta prueba, sólo tienes una variable de una única población(Fuente).

   • Hipótesis nula (H0): En la prueba de bondad de ajuste Chi-cuadrado, la hipótesis nula supone que no hay diferencia significativa entre el valor observado y el esperado(Fuente).

   • Hipótesis alternativa (Ha): En la prueba de bondad de ajuste Chi-cuadrado, la hipótesis alternativa supone que existe una diferencia significativa entre el valor observado y el esperado(Fuente).

     Por ejemplo, tomemos un ejemplo sencillo: lanzaste un dado justo de 6 caras 120 veces y obtuviste las frecuencias observadas.

Por tanto,

• H0 = Las probabilidades son iguales de obtener todos los números en la misma frecuencia, o los datos coinciden con los esperados.

          p1 = p2 = p3 = p4 = p5 = p6 = 1/6
  

• Ha = Al menos una p no es igual a 1/6, o los datos no coinciden con la esperada.

  • Criterios y regla de decisión: La región de rechazo es siempre de cola derecha utilizando la distribución χ2 con (k-1) grados de libertad. (k =número de categorías) Rechaza H0 si χ2calculado > χ2tabulado DOF = k-1

• Prueba de independencia la utilizas para probar si dos variables categóricas son independientes o no. p. ej., independencia del sexo frente a la opinión.

H0: La variable de fila es independiente de la variable de columna, o no hay relación significativa entre las variables Ha: La Relación es significativa.

• Criterios y regla de decisión: La región de rechazo es siempre de cola derecha utilizando la distribución χ2 con (r-1)(c-1) grados de libertad. (r = número de filas, c = número de columnas)

  Rechaza H0 si χ2calculado > χ2tabulado

  DOF = (r-1)(c-1)

1. Prueba de homogeneidad: Siempre que quieras comprobar si esas frecuencias de poblaciones diferentes se distribuyen de forma idéntica o no. En tales casos, realiza la prueba de homogeneidad. Veamos un ejemplo para comprenderlo de forma más práctica. En una encuesta, preguntaste por los ingresos como bajos, medios o altos. En esta encuesta, ambas poblaciones son diversas, como hombres y mujeres. En estos casos, realiza una prueba de homogeneidad chi-cuadrado para determinar si los ingresos de hombres y mujeres difieren significativamente o no.

H0: El recuento de frecuencias en toda la población es el mismo. Ha: El recuento de frecuencias en la población es diferente.

• Criterios y regla de decisión: La región de rechazo es siempre de cola derecha utilizando la distribución χ2 con (r-1)(c-1) grados de libertad. (r = número de filas, c = número de columnas)

  Rechaza H0 si χ2calculado > χ2tabulado

  DOF = (r-1)(c-1)

Ejemplo de la prueba Chi-cuadrado

Supón que quieres clasificar los defectos de los muebles producidos por una planta de fabricación en función del tipo de defectos y del turno de producción. Se registraron 390 defectos en muebles, y los defectos se clasificaron como uno de los cuatro tipos A, B, C y D. Al mismo tiempo, cada mueble defectuoso se identificó según el turno de producción.

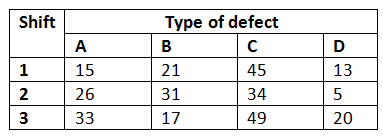
Fuente: Libro de Estadística en Ingeniería

Solución: tienes que mirar si los tipos de defecto dependen del turno de producción o no. Así que vamos a resolverlo utilizando Excel.

Resolver el ejemplo utilizando la prueba Chi-cuadrado en hojas de cálculo

Pongamos primero estos datos en la Hoja de Cálculo

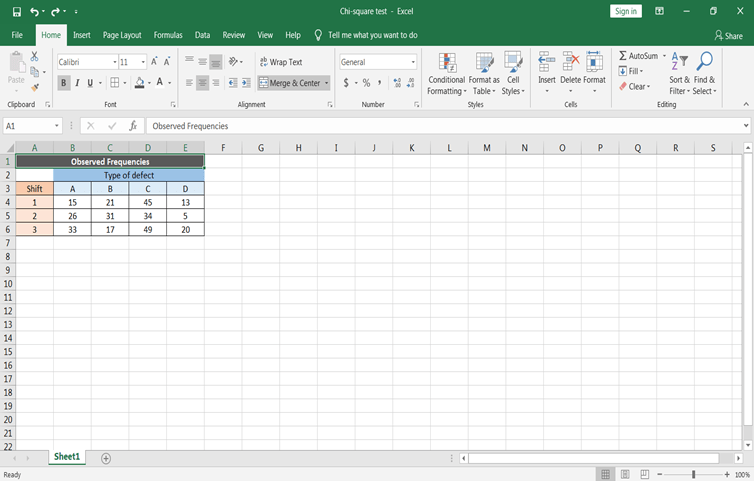
Definir la hipótesis nula y la hipótesis alternativa

Definir las hipótesis nula y alternativa en el apartado anterior. El objetivo principal es comprobar si los defectos de los muebles son independientes del turno de producción o no:

• H0 = El tipo de defecto y el turno de fabricación son independientes
• Ha = El tipo de defecto y el turno de fabricación son dependientes

Frecuencias esperadas calculadas

• Antes de calcular las frecuencias esperadas. En primer lugar, calcula la suma por filas de los elementos de cada fila y la suma por columnas de los elementos de cada columna mediante la función SUM(), lo que se conoce como total de filas y total de columnas, respectivamente. Calcula también el total del total de filas y el total de columnas. El total de filas y columnas será el mismo.

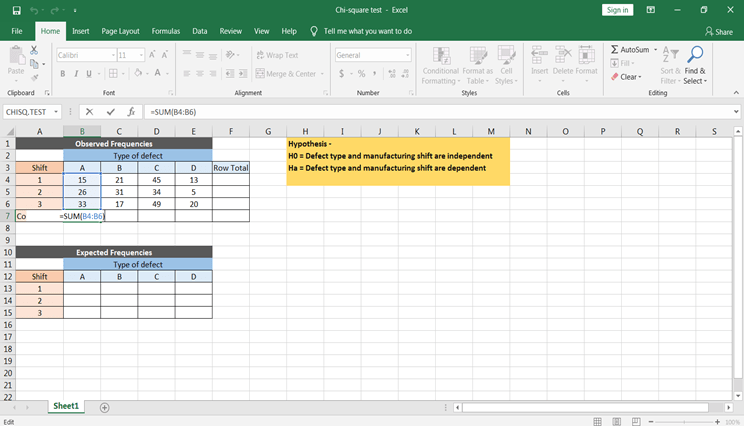
• Como sabes, la frecuencia esperada = (total de filas * total de columnas) / total

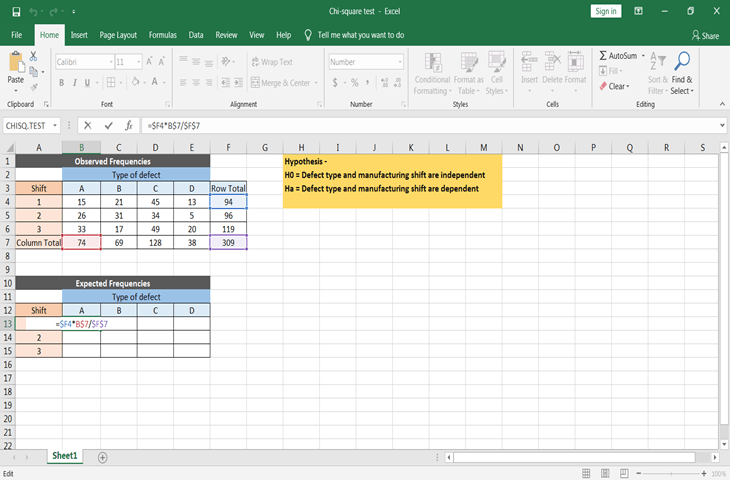
No olvides hacer absolutas las celdas al aplicar la fórmula, para que puedas copiar y pegar la fórmula para todos los valores previstos.

Calcula el valor del estadístico Chi

Ahora, antes de calcular el valor del estadístico Chi o valor p, vamos a suponer el nivel de significación. Esto significa a qué nivel de significación quieres conocer la respuesta. Supongamos un nivel de significación α = 0,05. Además, el grado de libertad sería = (r-1)(c-1) = (3-1)(4-1) = 6.

Ahora hay dos formas de calcular el valor estadístico chi-cuadrado, una mediante la fórmula χ^2= ∑(O-E)^2/E o utilizar la función excel para obtener el valor estadístico chi-cuadrado.

Primero vamos a calcular utilizando la fórmula. Para ello, tienes que calcular ∑(O-E)^2/E con Excel. Esto se puede hacer utilizando el siguiente paso -

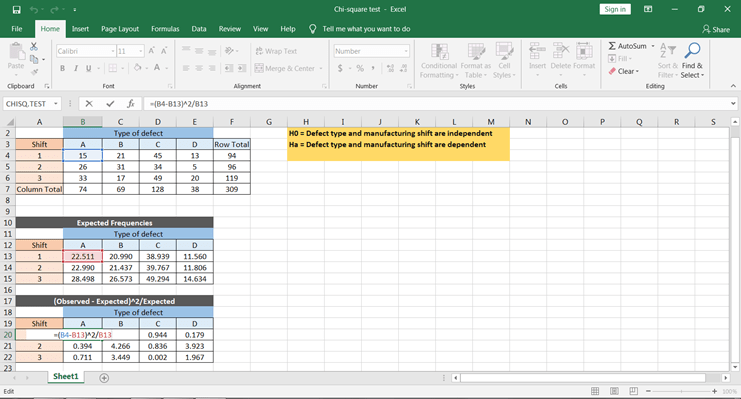
Puedes obtener todos los valores copiando y pegando esta fórmula en todas las celdas.

Para obtener los valores χ^2 hay que tomar la suma de todos los valores, lo que nos daría el valor calculado de la estadística chi-cuadrado.

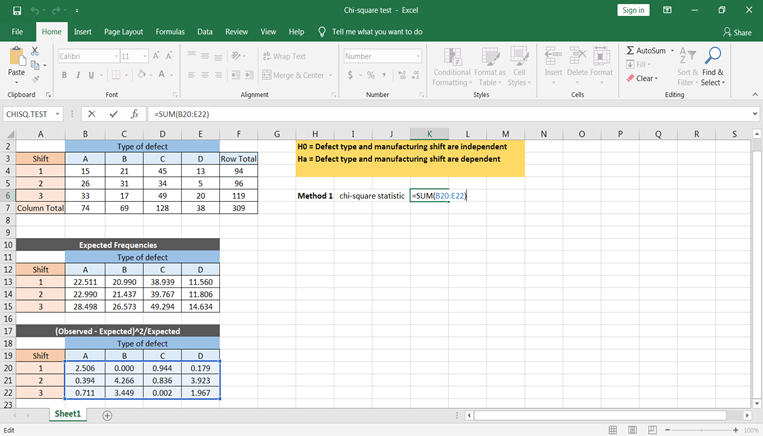
Basándote en el valor tabulado y calculado, puedes concluir que los tipos de defecto y los tiempos de turno son dependientes.

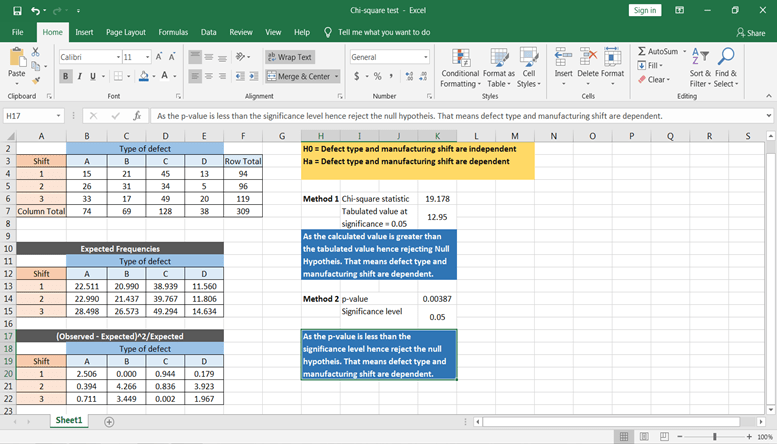
Ahora vamos a calcular utilizando la función excel. La función CHISQ.TEST() dará el valor p, que puede compararse directamente con el nivel de significación para concluir los resultados.

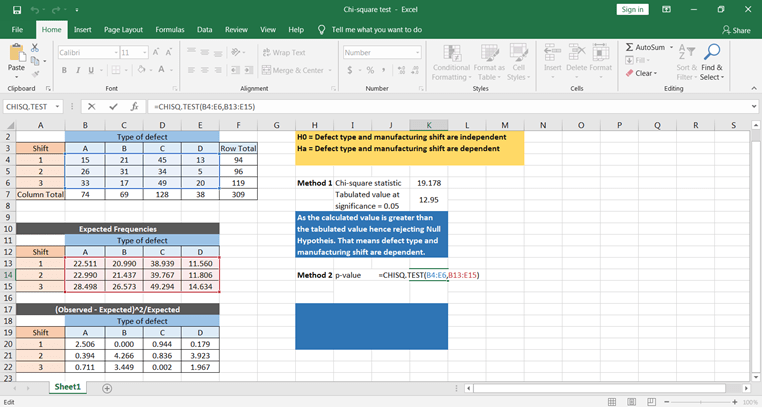
Basándote en el valor p, puedes concluir que el defecto depende del tiempo del turno de fabricación.

Ventajas e inconvenientes

Pros:

• Es más fácil de calcular.
• También puede utilizarse con datos nominales.
• No asume nada sobre la distribución de los datos.

Contras:

• El número de observaciones debe ser superior a 20.
• Los datos deben ser datos de frecuencia.
• Supone un muestreo aleatorio. Significa que la muestra debe seleccionarse aleatoriamente.
• Es sensible a las frecuencias pequeñas, lo que lleva a conclusiones erróneas.
• También es sensible al tamaño de la muestra.

Conclusión

Enhorabuena, ¡has llegado al final de este tutorial!

En este tutorial se han tratado muchos detalles de la prueba Chi-cuadrado. Has aprendido qué es la prueba Chi-cuadrado, terminologías utilizadas en la prueba Chi-cuadrado, tipos de pruebas Chi-cuadrado, ejemplos de pruebas Chi-cuadrado y un ejemplo sobre cómo resolver una prueba Chi-cuadrado en hojas de cálculo. Además, examinaste sus pros y sus contras.

Esperemos que ahora puedas utilizar los conceptos de Chi-cuadrado para probar la hipótesis. ¡Gracias por leer este tutorial!

Consulta nuestro tutorial Introducción a las hojas de cálculo.

Si te interesa aprender más sobre estadística en hojas de cálculo, sigue el curso Estadística en hojas de cálculo de DataCamp.