Optimización en Python: Técnicas, Paquetes y Buenas Prácticas

Técnicas de optimización en Python

Python ofrece una gran variedad de potentes técnicas para resolver problemas de optimización. Esto abarca desde métodos sencillos basados en el gradiente hasta algoritmos más complejos. Estas técnicas te permiten encontrar eficazmente los mínimos o máximos de funciones, ya sea en aprendizaje automático, ingeniería o investigación operativa. 

En esta sección, trataremos las técnicas de optimización que se suelen aplicar en Python, como el descenso del gradiente, el método de Newton, el método del gradiente conjugado, los métodos cuasi-Newton, el método Simplex y los métodos de región de confianza. 

Nota: Consulta este DataLab para ver todo el código utilizado para generar las visualizaciones de esta sección. 

¡Vamos a ello!

Descenso gradual

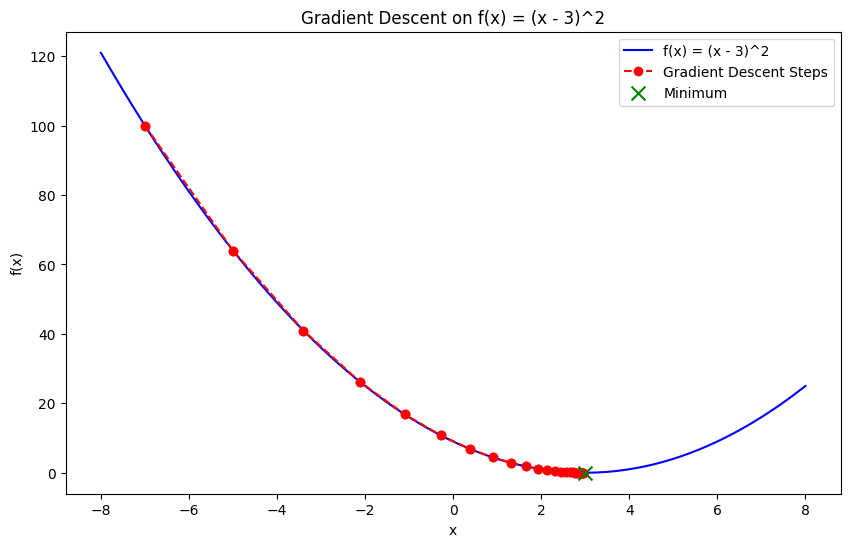
El descenso gradiente es una de las técnicas más fundamentales de la optimización numérica. Es un método iterativo utilizado para encontrar el mínimo de una función siguiendo el negativo del gradiente (o pendiente) de la función. 

La idea central es empezar con una conjetura inicial y actualizarla iterativamente moviéndose hacia el descenso más pronunciado hasta alcanzar la convergencia. Es una de las técnicas de optimización más utilizadas cuando se trata de entrenar modelos de aprendizaje automático, cuyo objetivo es minimizar la función de pérdida. 

Método de Newton

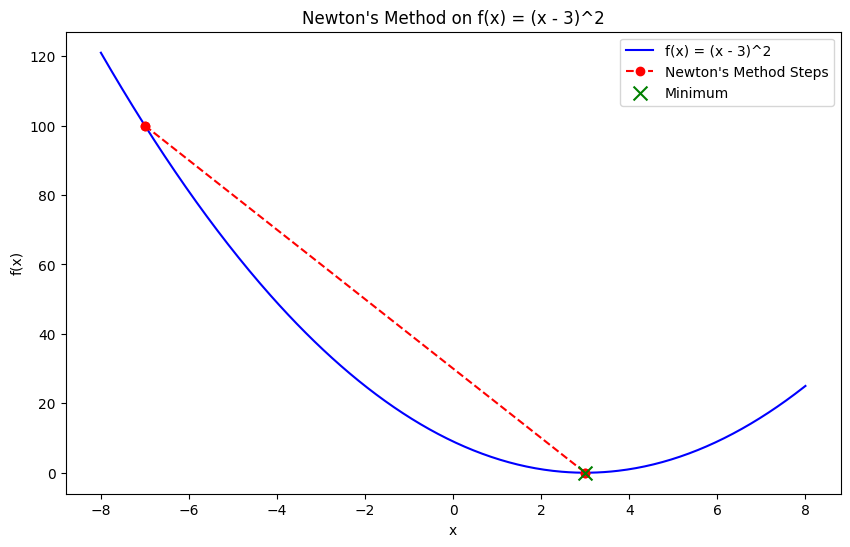
El método de Newton es una técnica de optimización que encuentra el mínimo utilizando tanto el gradiente como la derivada de segundo orden (la matriz hessiana) de la función objetivo. A diferencia del descenso de gradiente, que sólo se basa en derivadas de primer orden, el método de Newton aprovecha la información de curvatura, lo que permite una convergencia más rápida, especialmente para funciones convexas.

Aunque el método de Newton converge rápidamente, requiere calcular la matriz hessiana, lo que puede resultar caro computacionalmente y poco práctico para problemas a gran escala. Sin embargo, es muy eficaz para problemas convexos pequeños y suaves.

Método del gradiente conjugado

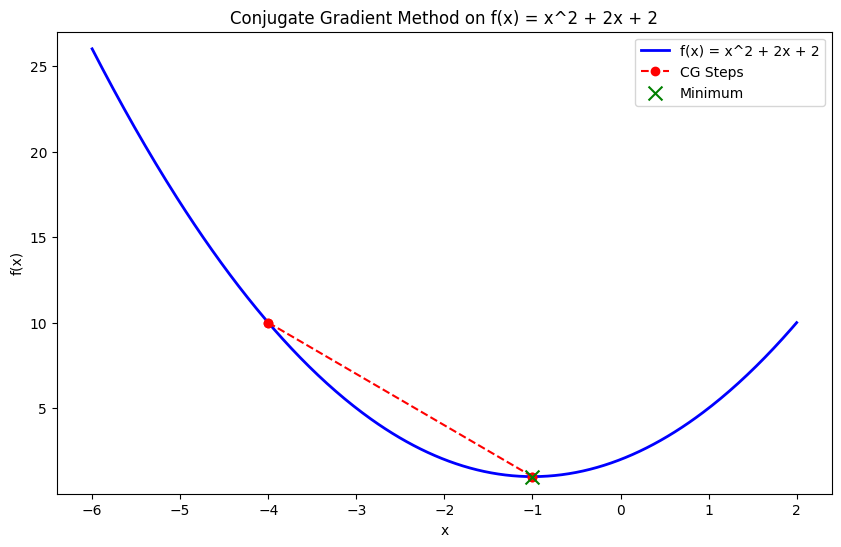
El método del gradiente conjugado es una técnica de optimización eficaz que se utiliza para problemas a gran escala, sobre todo cuando almacenar la matriz hessiana resulta poco práctico. Construye iterativamente direcciones conjugadas, optimizando a lo largo de ellas en lugar de requerir el hessiano completo, lo que lo hace adecuado para problemas como la minimización de funciones cuadráticas grandes.

Este método es útil en el análisis de elementos finitos o en aplicaciones de aprendizaje automático a gran escala, donde los cálculos matriciales se vuelven pesados.

Métodos cuasi-newton (BFGS)

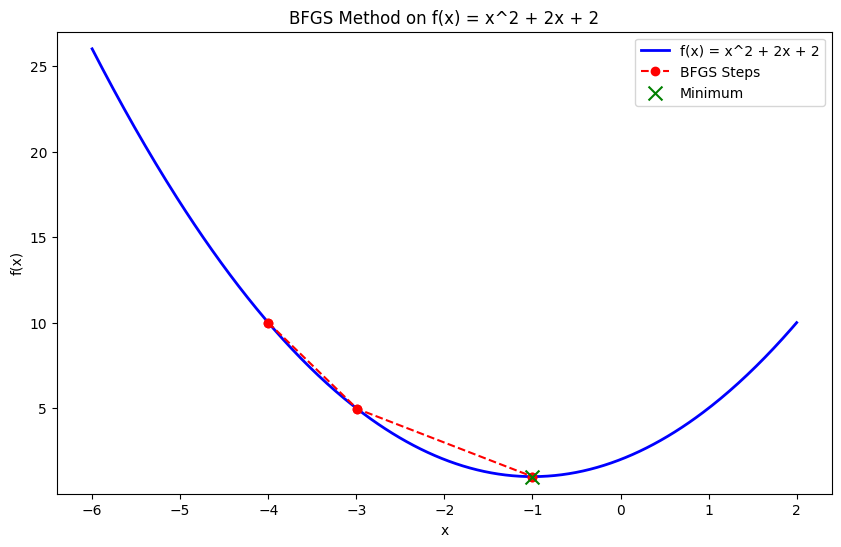
Los métodos Quasi-Newton, como el algoritmo Broyden-Fletcher-Goldfarb-Shanno (BFGS), aproximan la matriz hessiana en lugar de calcularla directamente. Estos métodos consiguen una convergencia más rápida que el descenso de gradiente al utilizar información de segundo orden sin la sobrecarga computacional de calcular el hessiano completo.

Método simplex

El método Simplex es un algoritmo muy utilizado para resolver problemas de programación lineal (PL), en los que la función objetivo y las restricciones son lineales. Examina sistemáticamente los vértices de la región factible (un poliedro) y avanza hacia el vértice óptimo donde la función objetivo alcanza su valor máximo o mínimo.

Métodos de región de confianza

Los métodos de región de confianza son algoritmos de optimización que construyen un modelo local de la función objetivo dentro de una "región de confianza" alrededor de la solución actual. 

En lugar de dar pasos en una dirección predeterminada (como en el descenso gradiente), el algoritmo define un subproblema más sencillo dentro de la región de confianza. Resuelve iterativamente este subproblema para afinar la solución. Estos métodos son especialmente eficaces para tratar problemas complejos y no lineales, y ofrecen una mayor estabilidad en comparación con los métodos tradicionales basados en el gradiente.

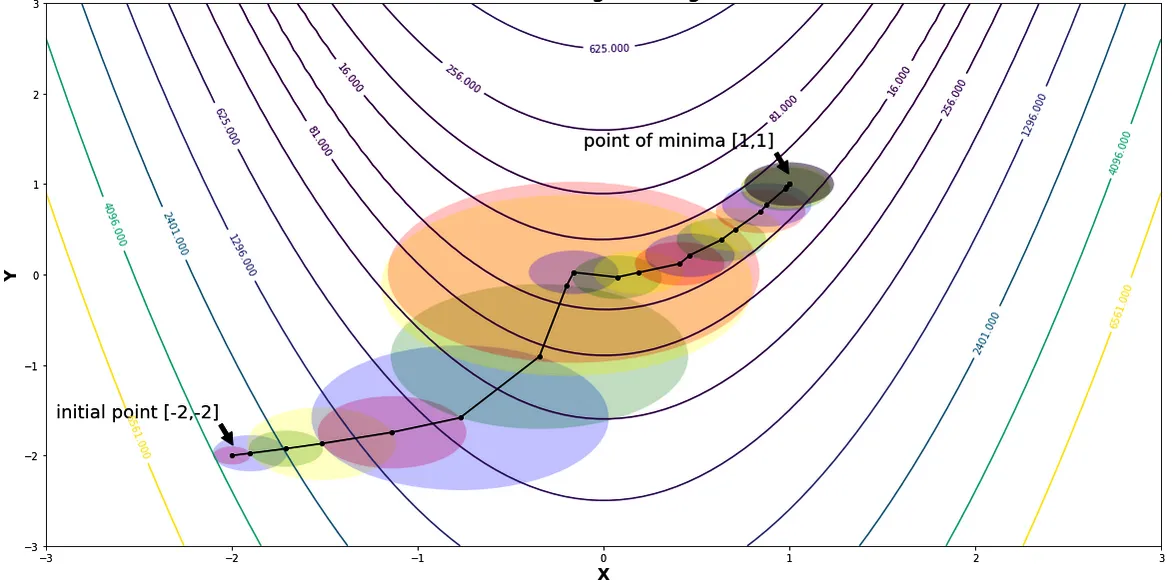
Regiones y radios de confianza minimizando la función de Rosenbrock | Fuente: Métodos de región de confianza por Shivangi Khare

Paquetes Python comunes para la optimización

Hay una serie de bibliotecas y paquetes diseñados para facilitar la optimización numérica. Cada uno tiene sus puntos fuertes y sus aplicaciones, pero independientemente del problema de optimización al que te enfrentes, suele haber una herramienta robusta que te ayude a abordarlo en Python. 

Aquí tienes cuatro de los paquetes de optimización más comunes:  

Optimización SciPy (scipy.optimize)

El módulo scipy.optimize es una biblioteca versátil del ecosistema SciPy, que ofrece una amplia gama de algoritmos para problemas de optimización tanto sin restricciones como con restricciones. Incluye funciones para encontrar los mínimos de funciones escalares y multivariables, resolver problemas de búsqueda de raíces y ajustar curvas a datos.

Las funciones de este módulo incluyen: 

• minimize(): Función utilizada para minimizar una función escalar de una o varias variables.

from scipy.optimize import minimize

def objective_function(x):
    return x[0]**2 + x[1]**2
result = minimize(objective_function, [1, 1], method='BFGS')
print(result.x)  # Optimal solution

# >>> [-1.07505143e-08 -1.07505143e-08]

• root(): Encuentra la raíz de una función vectorial: muy útil para resolver sistemas de ecuaciones no lineales.

from scipy.optimize import root

def equations(vars):
    x, y = vars
    return [x + 2*y - 3, x - y - 1]
result = root(equations, [0, 0])
print(result.x)

# >>> [1.66666667 0.66666667]

• curve_fit(): Esta función ajusta una curva a un conjunto de puntos de datos y es útil para ajustar datos y estimar parámetros.

from scipy.optimize import curve_fit
import numpy as np

def model(x, a, b):
    return a * np.exp(b * x)
x_data = np.array([1, 2, 3])
y_data = np.array([2.7, 7.4, 20.1])
params, covariance = curve_fit(model, x_data, y_data)
print(params)  # Fitted parameters

# >>> [0.9981286  1.00089935]

CVXPY

CVXPY es una biblioteca de Python diseñada para problemas de optimización convexa. Permite a los usuarios definir y resolver estos problemas mediante una sintaxis declarativa de alto nivel. Simplifica la formulación de problemas de optimización complejos permitiendo a los usuarios especificar la función objetivo y las restricciones de forma natural y legible.

CVXPY ofrece las siguientes funciones:

• Sintaxis declarativa: CVXPY proporciona una forma intuitiva de modelar problemas de optimización utilizando las expresiones matemáticas de Python.
• Solucionadores de última generación: Interactúa con solucionadores avanzados como ECOS, SCS y OSQP, que tratan eficazmente los problemas convexos.

import cvxpy as cp

# Define variables
x = cp.Variable()
y = cp.Variable()

# Define constraints
constraints = [x + y == 1, x - y >= 2]

# Define the objective function
objective = cp.Minimize(x**2 + y**2)

# Formulate the problem
prob = cp.Problem(objective, constraints)

# Solve the problem
result = prob.solve()
print(f"Optimal value: {result}")
print(f"x: {x.value}, y: {y.value}")

# >>> Optimal value: 2.5
# x: 1.5, y: -0.5000000000000001

Pyomo

Pyomo es un paquete de modelización de optimización flexible y completo que admite programación lineal, no lineal y mixta entera. Está diseñado para problemas de optimización complejos y se integra perfectamente con solucionadores como GLPK, CBC y CPLEX.

Las características de Pyomo incluyen:

• Flexibilidad de modelado: Pyomo permite definir problemas de optimización con un alto grado de flexibilidad, incluyendo restricciones y objetivos complejos.
• Integración del solucionador: Admite una amplia gama de solucionadores, lo que proporciona flexibilidad a la hora de elegir la mejor herramienta para un problema concreto.

Gurobi y CPLEX (mediante Pyomo o API directa)

Gurobi y CPLEX son solucionadores de alto rendimiento para problemas de optimización a gran escala. Se utilizan habitualmente en la industria para tareas como la optimización de la cadena de suministro, la gestión de carteras y la logística. 

Ofrecen algoritmos avanzados diseñados para gestionar eficazmente problemas complejos y a gran escala.

• Gurobi: Accesible a través de Pyomo o de su API directa, Gurobi es conocido por su velocidad y fiabilidad en la resolución de problemas de programación lineal, entera y cuadrática.
• CPLEX: Del mismo modo, CPLEX proporciona potentes capacidades de optimización y se utiliza en diversos sectores para resolver complejos problemas operativos y estratégicos. Se puede acceder a él a través de Pyomo o directamente a través de su API.

Estos solucionadores se emplean a menudo para problemas a escala industrial en los que la eficacia y la solidez computacionales son fundamentales.

Aplicaciones reales de la optimización numérica en Python

Como he mencionado en la introducción, la optimización numérica desempeña un papel crucial en diversos ámbitos. Proporciona técnicas esenciales para resolver problemas complejos y tomar decisiones basadas en datos.

Por ejemplo:  

• Aprendizaje automático: Los modelos se entrenan fundamentalmente mediante optimización numérica. Esto implica encontrar los parámetros óptimos que minimicen la función de pérdida y cuantificar lo bien que el modelo predice la variable objetivo. 
• Investigación operativa: Las técnicas de optimización ayudan a tomar decisiones estratégicas que maximizan o minimizan diversas métricas operativas. Optimizando funciones objetivo sujetas a restricciones, los investigadores de operaciones pueden mejorar la eficacia en procesos como la gestión de la cadena de suministro, la programación de la mano de obra y la planificación de la producción. 
• Finanzas: La optimización numérica es crucial en el sector financiero para tareas como la optimización de carteras. Ayuda a determinar la mejor asignación de activos para maximizar los rendimientos o minimizar el riesgo.
• Diseño de ingeniería: La optimización numérica se aplica para diseñar sistemas y estructuras que cumplan criterios específicos de rendimiento minimizando los costes. Este proceso ayuda a conseguir diseños eficientes para todo, desde puentes y aviones hasta procesos de fabricación y sistemas energéticos.

Buenas prácticas para la optimización numérica en Python

Hay que tener en cuenta varios factores para garantizar los mejores resultados de tus esfuerzos de optimización en Python. Asegúrate de seguir las siguientes buenas prácticas: 

Elegir el algoritmo correcto

Seleccionar el algoritmo de optimización adecuado es crucial para conseguir resultados óptimos. La elección del algoritmo depende de la naturaleza del problema:

• Lineal frente a no lineal: Para los problemas lineales, son adecuadas las técnicas de programación lineal como los métodos Simplex o de punto interior. Para los problemas no lineales, pueden ser más adecuados métodos como el descenso del gradiente, el método de Newton o los métodos cuasi-Newton (por ejemplo, BFGS).
• Restringido frente a no restringido: Para los problemas con restricciones, se necesitan algoritmos como la Programación Cuadrática Secuencial (PCS) o métodos que manejen las restricciones de forma nativa (por ejemplo, métodos de punto interior). Los problemas sin restricciones pueden resolverse eficazmente mediante el descenso de gradiente o el método de Newton.

Elegir el algoritmo correcto en función de las características del problema ayuda a conseguir una convergencia más rápida y soluciones más precisas.

Restricciones de manipulación

Las restricciones en los problemas de optimización pueden influir significativamente en la elección del algoritmo y de la estrategia de solución. Se pueden utilizar varios enfoques para gestionar las restricciones:

• Métodos de penalización: Incorpora las restricciones a la función objetivo añadiendo un término de penalización por violación de las restricciones. Este enfoque transforma un problema restringido en uno no restringido, lo que permite utilizar métodos de optimización no restringidos.
• Métodos de barrera: Utiliza funciones barrera para garantizar que no se violan las restricciones. Los métodos de barrera funcionan incluyendo un término de barrera en la función objetivo que se hace infinito a medida que nos acercamos a las restricciones.
• Soporte nativo: Utiliza solucionadores que admitan intrínsecamente restricciones. Muchos solucionadores de optimización modernos, como los disponibles en scipy.optimize o CVXPY, están diseñados para manejar las restricciones directa y eficazmente.

Seleccionar el método adecuado para tratar las restricciones garantiza que las soluciones sean factibles y cumplan todos los requisitos especificados.

Escalado y preprocesado

Un escalado y preprocesado adecuados de los datos pueden mejorar significativamente el rendimiento de los algoritmos de optimización:

• Escala: Normaliza o estandariza los datos de entrada para garantizar que las características contribuyan por igual a la función objetivo. Esto puede evitar problemas relacionados con la estabilidad numérica y mejorar los índices de convergencia.
• Preprocesamiento: Aplica técnicas como la ingeniería de rasgos o la reducción de la dimensionalidad para simplificar el problema. Un preprocesamiento adecuado reduce la complejidad del problema de optimización y acelera el proceso de solución.

Interpretar los resultados

Interpretar los resultados de los algoritmos de optimización implica comprender varios aspectos:

• Calidad de la solución: Evalúa la calidad de la solución comprobando si satisface las condiciones y restricciones óptimas. Compara los resultados con puntos de referencia conocidos o valídalos utilizando técnicas de validación cruzada.
• Criterios de convergencia: Evalúa si el algoritmo de optimización ha convergido comprobando los mensajes de convergencia, los recuentos de iteraciones o los cambios en el valor de la función objetivo. Asegúrate de que el algoritmo ha alcanzado una solución próxima al verdadero óptimo.
• Precisión numérica: Considera el impacto de la precisión numérica en los resultados. Los errores numéricos menores pueden acumularse y afectar a la solución final, sobre todo en problemas a gran escala o con tolerancias estrechas.

Conclusión

La optimización numérica es una piedra angular de la resolución de problemas moderna. Ofrece potentes herramientas para afrontar retos complejos en campos como el aprendizaje automático, la ingeniería, las finanzas y la investigación operativa. 

El rico ecosistema de bibliotecas de optimización de Python -como SciPy, CVXPY y Pyomo- hace que estas técnicas avanzadas sean más accesibles, permitiendo a investigadores, ingenieros y científicos de datos diseñar sistemas eficientes, optimizar modelos y tomar decisiones más inteligentes basadas en datos. 

Armado con las técnicas adecuadas y las mejores prácticas, ahora estás bien equipado para abordar y resolver incluso los problemas de optimización más desafiantes en Python. Pero consulta estos recursos para seguir aprendiendo:

• Introducción a la Optimización en Python
• Introducción a la Modelización Lineal en Python
• Hoja de trucos SciPy: Álgebra lineal en Python
• Estructuras de datos: Una guía completa con ejemplos en Python