Otimização em Python: Técnicas, pacotes e práticas recomendadas

Técnicas de otimização em Python

O Python oferece uma variedade de técnicas poderosas para que você possa resolver problemas de otimização. Isso varia de métodos simples baseados em gradiente a algoritmos mais complexos. Essas técnicas permitem que você encontre eficientemente os mínimos ou máximos de funções, seja em machine learning, engenharia ou pesquisa operacional. 

Nesta seção, abordaremos as técnicas de otimização comumente implementadas em Python, incluindo a descida de gradiente, o método de Newton, o método de gradiente conjugado, os métodos quase-Newton, o método Simplex e os métodos trust-region. 

Observação: Confira este DataLab para ver todo o código usado para gerar as visualizações nesta seção. 

Vamos lá!

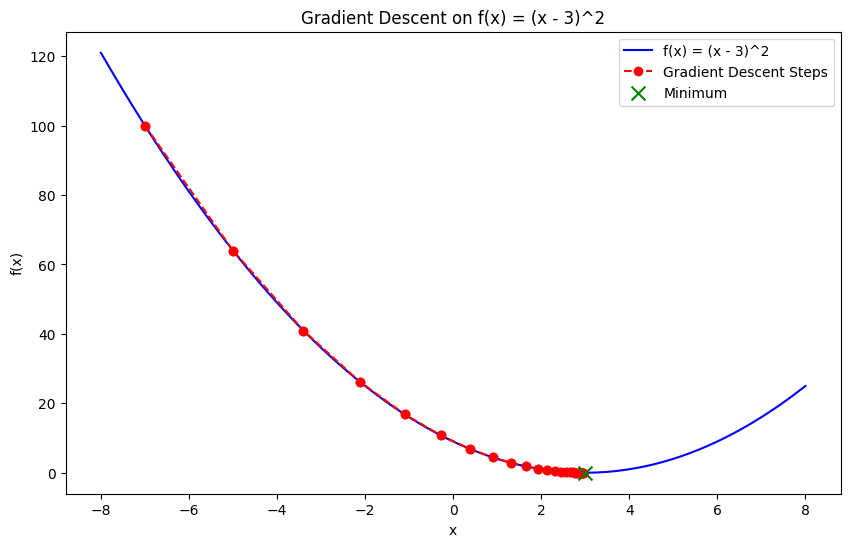
Descida de gradiente

A descida de gradiente é uma das técnicas mais fundamentais na otimização numérica. É um método iterativo usado para encontrar o mínimo de uma função seguindo o negativo do gradiente (ou inclinação) da função. 

A ideia central é começar com um palpite inicial e atualizá-lo iterativamente, movendo-se em direção à descida mais íngreme até que a convergência seja alcançada. É uma das técnicas de otimização mais comumente usadas quando se trata de treinar modelos de machine learning, em que o objetivo é minimizar a função de perda. 

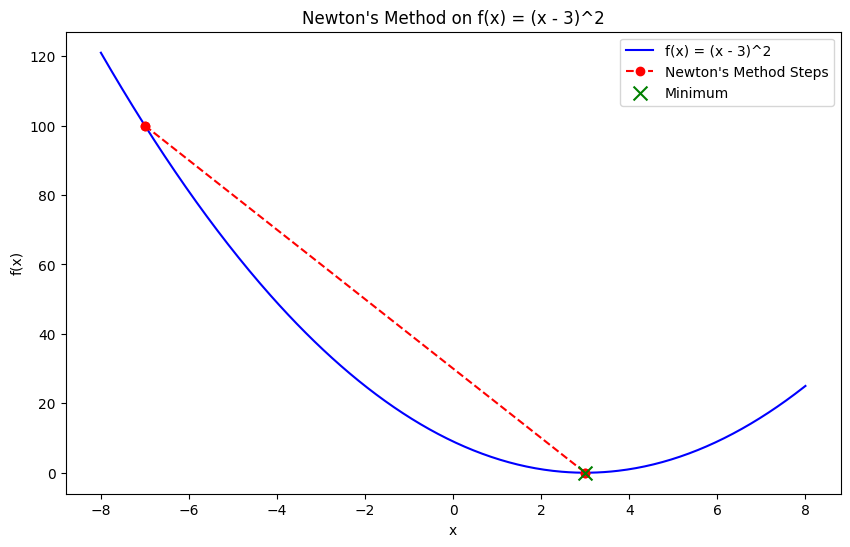
Método de Newton

O método de Newton é uma técnica de otimização que encontra o mínimo usando tanto o gradiente quanto a derivada de segunda ordem (a matriz Hessiana) da função objetiva. Diferentemente da descida de gradiente, que se baseia apenas nas derivadas de primeira ordem, o método de Newton aproveita as informações de curvatura, permitindo uma convergência mais rápida, especialmente para funções convexas.

Embora o método de Newton converse rapidamente, ele exige o cálculo da matriz Hessiana, o que pode ser computacionalmente caro e impraticável para problemas de grande escala. No entanto, ele é altamente eficaz para problemas convexos pequenos e suaves.

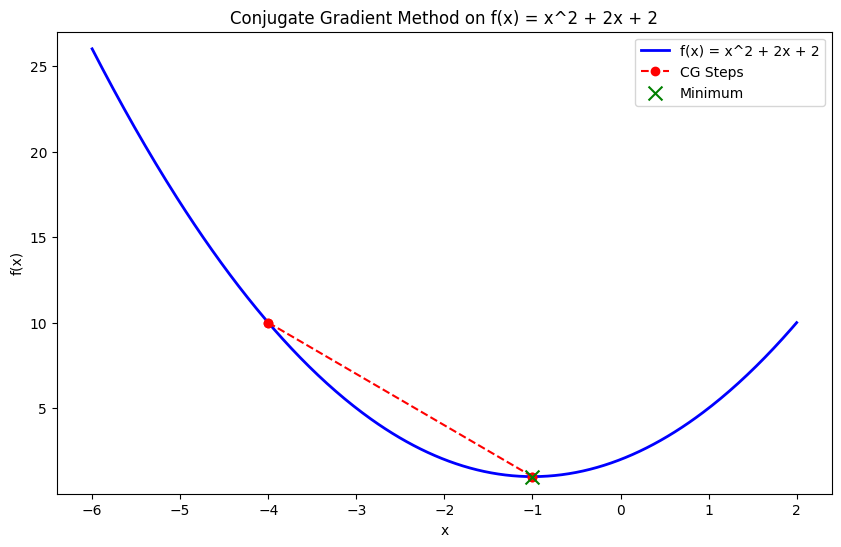
Método de gradiente conjugado

O método de gradiente conjugado é uma técnica de otimização eficiente usada para problemas de grande escala, especialmente quando o armazenamento da matriz Hessiana é impraticável. Ele cria iterativamente direções conjugadas, otimizando ao longo delas em vez de exigir o Hessiano completo, o que o torna adequado para problemas como a minimização de funções quadráticas grandes.

Esse método é útil na análise de elementos finitos ou em aplicativos de machine learning em grande escala, em que os cálculos de matriz se tornam onerosos.

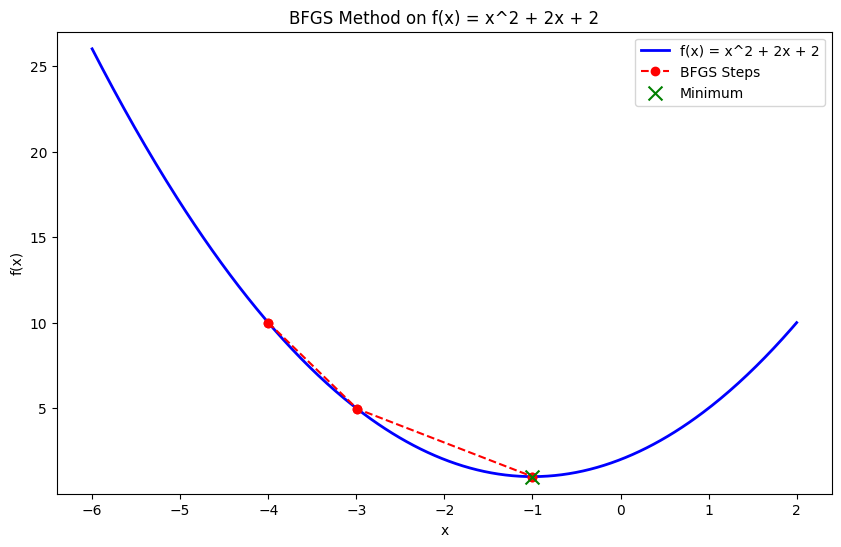
Métodos quase newtonianos (BFGS)

Os métodos Quasi-Newton, como o algoritmo Broyden-Fletcher-Goldfarb-Shanno (BFGS), aproximam a matriz Hessiana em vez de calculá-la diretamente. Esses métodos alcançam uma convergência mais rápida do que a descida de gradiente, utilizando informações de segunda ordem sem a sobrecarga computacional de calcular o Hessiano completo.

Método Simplex

O método Simplex é um algoritmo amplamente usado para resolver problemas de programação linear (LP), em que a função objetiva e as restrições são lineares. Ele examina sistematicamente os vértices da região viável (um poliedro) e se move em direção ao vértice ideal onde a função objetiva atinge seu valor máximo ou mínimo.

Métodos de região de confiança

Os métodos de região de confiança são algoritmos de otimização que criam um modelo local da função objetiva em uma "região de confiança" em torno da solução atual. 

Em vez de seguir etapas em uma direção predeterminada (como na descida de gradiente), o algoritmo define um subproblema mais simples dentro da região de confiança. Ele resolve esse subproblema de forma iterativa para refinar a solução. Esses métodos são particularmente eficazes para lidar com problemas complexos e não lineares e oferecem melhor estabilidade em comparação com os métodos tradicionais baseados em gradiente.

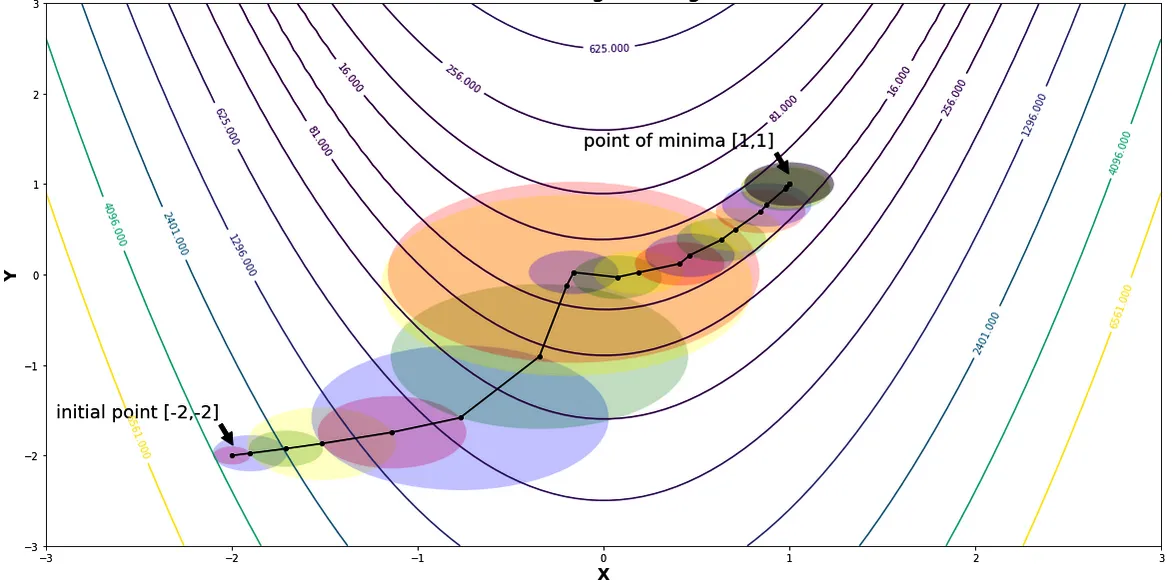
Regiões e raios confiáveis enquanto minimizam a função de Rosenbrock | Fonte Métodos de região de confiança por Shivangi Khare

Pacotes comuns do Python para otimização

Há uma série de bibliotecas e pacotes projetados para facilitar a otimização numérica. Cada uma tem seus pontos fortes e aplicações, mas, independentemente do problema de otimização que você enfrenta, geralmente há uma ferramenta robusta para ajudá-lo a resolvê-lo em Python. 

Aqui estão quatro dos pacotes de otimização mais comuns:  

Otimização do SciPy (scipy.optimize)

O módulo scipy.optimize é uma biblioteca versátil no ecossistema SciPy, que oferece uma ampla variedade de algoritmos para problemas de otimização com e sem restrições. Ele inclui funções para encontrar os mínimos de funções escalares e multivariáveis, resolver problemas de busca de raízes e ajustar curvas aos dados.

As funções desse módulo incluem: 

• minimize(): Uma função usada para minimizar uma função escalar de uma ou mais variáveis.

from scipy.optimize import minimize

def objective_function(x):
    return x[0]**2 + x[1]**2
result = minimize(objective_function, [1, 1], method='BFGS')
print(result.x)  # Optimal solution

# >>> [-1.07505143e-08 -1.07505143e-08]

• root(): Encontra a raiz de uma função vetorial - extremamente útil para resolver sistemas de equações não lineares.

from scipy.optimize import root

def equations(vars):
    x, y = vars
    return [x + 2*y - 3, x - y - 1]
result = root(equations, [0, 0])
print(result.x)

# >>> [1.66666667 0.66666667]

• curve_fit(): Essa função ajusta uma curva a um conjunto de pontos de dados e é útil para ajustar dados e estimar parâmetros.

from scipy.optimize import curve_fit
import numpy as np

def model(x, a, b):
    return a * np.exp(b * x)
x_data = np.array([1, 2, 3])
y_data = np.array([2.7, 7.4, 20.1])
params, covariance = curve_fit(model, x_data, y_data)
print(params)  # Fitted parameters

# >>> [0.9981286  1.00089935]

CVXPY

CVXPY é uma biblioteca Python projetada para problemas de otimização convexa. Ele permite que os usuários definam e resolvam esses problemas usando uma sintaxe declarativa de alto nível. Ele simplifica a formulação de problemas complexos de otimização, permitindo que os usuários especifiquem a função objetiva e as restrições de forma natural e legível.

O CVXPY oferece os seguintes recursos:

• Sintaxe declarativa: O CVXPY fornece uma maneira intuitiva de modelar problemas de otimização usando as expressões matemáticas do Python.
• Solucionadores de última geração: Ele faz interface com solucionadores avançados, como ECOS, SCS e OSQP, que lidam com eficiência com problemas convexos.

import cvxpy as cp

# Define variables
x = cp.Variable()
y = cp.Variable()

# Define constraints
constraints = [x + y == 1, x - y >= 2]

# Define the objective function
objective = cp.Minimize(x**2 + y**2)

# Formulate the problem
prob = cp.Problem(objective, constraints)

# Solve the problem
result = prob.solve()
print(f"Optimal value: {result}")
print(f"x: {x.value}, y: {y.value}")

# >>> Optimal value: 2.5
# x: 1.5, y: -0.5000000000000001

Pyomo

O Pyomo é um pacote de modelagem de otimização flexível e abrangente que oferece suporte à programação linear, não linear e mista de números inteiros. Ele foi projetado para problemas complexos de otimização e se integra perfeitamente a solucionadores como GLPK, CBC e CPLEX.

Os recursos do Pyomo incluem:

• Flexibilidade de modelagem: O Pyomo permite a definição de problemas de otimização com um alto grau de flexibilidade, incluindo restrições e objetivos complexos.
• Integração do solucionador: Ele oferece suporte a uma ampla gama de solucionadores, proporcionando flexibilidade na escolha da melhor ferramenta para um problema específico.

Gurobi e CPLEX (via Pyomo ou API direta)

O Gurobi e o CPLEX são solucionadores de alto desempenho para problemas de otimização em larga escala. Eles são comumente usados no setor para tarefas como otimização da cadeia de suprimentos, gerenciamento de portfólio e logística. 

Eles oferecem algoritmos avançados projetados para lidar com problemas complexos e de grande escala de forma eficiente.

• Gurobi: Acessível por meio do Pyomo ou de sua API direta, o Gurobi é conhecido por sua velocidade e confiabilidade na solução de problemas de programação linear, inteira e quadrática.
• CPLEX: Da mesma forma, o CPLEX oferece recursos avançados de otimização e é usado em vários setores para resolver problemas operacionais e estratégicos complexos. Ele pode ser acessado via Pyomo ou diretamente por meio de sua API.

Esses solucionadores são frequentemente empregados em problemas de escala industrial em que a eficiência computacional e a robustez são fundamentais.

Aplicações reais de otimização numérica em Python

Como mencionei na introdução, a otimização numérica desempenha um papel fundamental em vários domínios. Ele fornece técnicas essenciais para resolver problemas complexos e tomar decisões baseadas em dados.

Por exemplo:  

• Machine learning: Os modelos são fundamentalmente treinados usando otimização numérica. Isso envolve encontrar os parâmetros ideais que minimizem a função de perda e quantificar a qualidade da previsão do modelo para a variável-alvo. 
• Pesquisa operacional: As técnicas de otimização ajudam a tomar decisões estratégicas que maximizam ou minimizam várias métricas operacionais. Ao otimizar as funções objetivas sujeitas a restrições, os pesquisadores de operações podem melhorar a eficiência em processos como gerenciamento da cadeia de suprimentos, programação da força de trabalho e planejamento da produção. 
• Finanças: A otimização numérica é crucial no setor financeiro para tarefas como a otimização de portfólio. Ele ajuda a determinar a melhor alocação de ativos para maximizar os retornos ou minimizar os riscos.
• Projeto de engenharia: A otimização numérica é aplicada para projetar sistemas e estruturas que atendam a critérios específicos de desempenho e, ao mesmo tempo, minimizem os custos. Esse processo ajuda a obter projetos eficientes para tudo, desde pontes e aeronaves até processos de fabricação e sistemas de energia.

Práticas recomendadas para otimização numérica em Python

Vários fatores devem ser considerados para garantir os melhores resultados de seus esforços de otimização em Python. Certifique-se de seguir as práticas recomendadas a seguir: 

Escolhendo o algoritmo correto

A seleção do algoritmo de otimização correto é fundamental para que você obtenha os melhores resultados. A escolha do algoritmo depende da natureza do problema:

• Linear vs. não linear: Para problemas lineares, as técnicas de programação linear, como os métodos Simplex ou de ponto interior, são apropriadas. Para problemas não lineares, métodos como descida de gradiente, método de Newton ou métodos quase-Newton (por exemplo, BFGS) podem ser mais adequados.
• Restrito vs. irrestrito: Para problemas com restrições, são necessários algoritmos como o SQP (Sequential Quadratic Programming, programação quadrática sequencial) ou métodos que lidem com restrições nativamente (por exemplo, métodos de ponto interior). Os problemas sem restrições podem ser resolvidos com eficiência usando a descida de gradiente ou o método de Newton.

A escolha do algoritmo correto com base nas características do problema ajuda a obter uma convergência mais rápida e soluções mais precisas.

Restrições de manuseio

As restrições nos problemas de otimização podem afetar significativamente a escolha do algoritmo e da estratégia de solução. Várias abordagens podem ser usadas para lidar com as restrições:

• Métodos de penalidade: Incorporar restrições à função objetiva adicionando um termo de penalidade para violações de restrições. Essa abordagem transforma um problema com restrições em um problema sem restrições, permitindo o uso de métodos de otimização sem restrições.
• Métodos de barreira: Use funções de barreira para garantir que as restrições não sejam violadas. Os métodos de barreira funcionam com a inclusão de um termo de barreira na função objetiva que se torna infinito à medida que as restrições se aproximam.
• Suporte nativo: Utilize solucionadores que suportem restrições de forma inerente. Muitos solucionadores de otimização modernos, como os disponíveis em scipy.optimize ou CVXPY, foram projetados para lidar com restrições de forma direta e eficiente.

A seleção do método apropriado para lidar com as restrições garante que as soluções sejam viáveis e atendam a todos os requisitos especificados.

Dimensionamento e pré-processamento

O dimensionamento e o pré-processamento adequados dos dados podem melhorar significativamente o desempenho dos algoritmos de otimização:

• Dimensionamento: Normalize ou padronize os dados de entrada para garantir que os recursos contribuam igualmente para a função objetiva. Isso pode evitar problemas relacionados à estabilidade numérica e melhorar as taxas de convergência.
• Pré-processamento: Aplique técnicas como engenharia de recursos ou redução de dimensionalidade para simplificar o problema. O pré-processamento adequado reduz a complexidade do problema de otimização e acelera o processo de solução.

Interpretação dos resultados

A interpretação dos resultados dos algoritmos de otimização envolve a compreensão de vários aspectos:

• Qualidade da solução: Avalie a qualidade da solução verificando se ela satisfaz as condições e restrições ideais. Compare os resultados com benchmarks conhecidos ou valide-os usando técnicas de validação cruzada.
• Critérios de convergência: Avalie se o algoritmo de otimização convergiu verificando as mensagens de convergência, as contagens de iteração ou as alterações no valor da função objetiva. Assegure-se de que o algoritmo tenha alcançado uma solução próxima do ótimo real.
• Precisão numérica: Considere o impacto da precisão numérica nos resultados. Pequenos erros numéricos podem se acumular e afetar a solução final, principalmente em problemas de grande escala ou com tolerâncias apertadas.

Conclusão

A otimização numérica é uma pedra angular da solução de problemas modernos. Ele oferece ferramentas poderosas para que você possa enfrentar desafios complexos em áreas como machine learning, engenharia, finanças e pesquisa operacional. 

O rico ecossistema de bibliotecas de otimização do Python, como SciPy, CVXPY e Pyomo, torna essas técnicas avançadas mais acessíveis, capacitando pesquisadores, engenheiros e cientistas de dados a projetar sistemas eficientes, otimizar modelos e tomar decisões mais inteligentes e orientadas por dados. 

Munido das técnicas corretas e das práticas recomendadas, agora você está bem equipado para abordar e resolver até mesmo os problemas de otimização mais desafiadores em Python. Mas confira estes recursos para continuar aprendendo:

• Introdução à otimização em Python
• Introdução à modelagem linear em Python
• Folha de dicas do SciPy: Álgebra linear em Python
• Estruturas de dados: Um guia abrangente com exemplos em Python