Tutorial de análisis de componentes principales en R

Introducción al análisis de componentes principales (ACP)

Como científico de datos del sector minorista, imagina que intentas comprender qué hace feliz a un cliente a partir de un conjunto de datos que contiene estas cinco características: gasto mensual, edad, sexo, frecuencia de compra y valoración del producto. Para analizar y extraer conclusiones procesables mejor, debemos comprender el conjunto de datos o, como mínimo, visualizarlo. Los seres humanos no pueden visualizar fácilmente más de tres dimensiones, por lo que visualizar datos de clientes con cinco características (dimensiones) no es sencillo. Aquí es donde entra en juego el análisis de componentes principales (PCA). 

"Pero ¿qué es el análisis de componentes principales?"

Es un enfoque estadístico que puede utilizarse para analizar datos de alta dimensión y captar de ellos la información más importante. Esto se hace transformando los datos originales en un espacio de menor dimensión y agrupando las variables altamente correlacionadas. En nuestro caso, el PCA elegiría tres características, como el gasto mensual, la frecuencia de compra y la valoración del producto. Esto podría facilitar la visualización y comprensión de los datos.

Después de este tutorial, comprenderás mejor el análisis de componentes principales y cómo aplicarlo a casos reales utilizando el famoso paquete corrr de R.

Mira y aprende más sobre el análisis de componentes principales en R en este vídeo de nuestro curso.

¿Cómo funciona el PCA? Guía en 5 pasos

Aunque nos centremos en el PCA, tengamos en cuenta las siguientes cinco técnicas principales de componentes principales, cuyo objetivo es resumir y visualizar datos multivariante. El PCA, a diferencia de las demás técnicas, solo funciona con variables cuantitativas. 

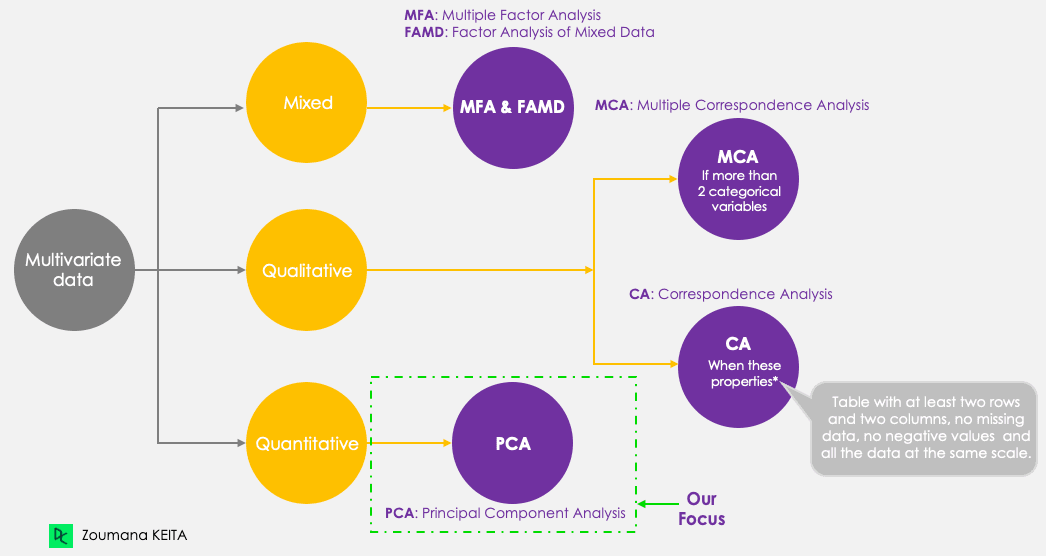
Métodos de componentes principales

No entraremos en la explicación del concepto matemático, que puede ser algo complejo.  Sin embargo, comprender los cinco pasos siguientes puede dar una mejor idea de cómo computar el PCA. 

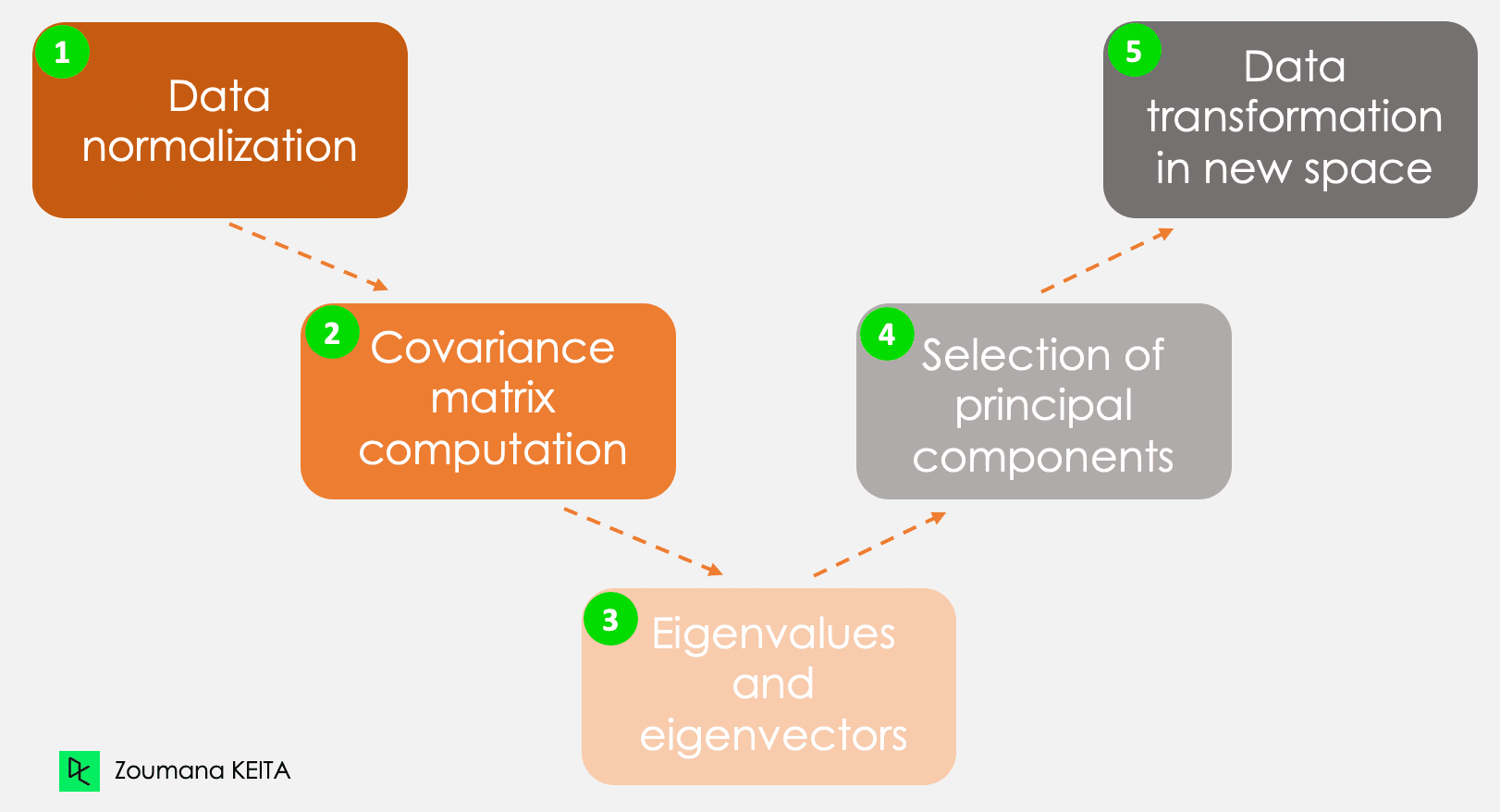
Los cinco pasos principales para computar los componentes principales

Paso 1: normalización de datos

Pensando en el ejemplo de la introducción, consideremos, por ejemplo, la siguiente información para un cliente determinado. 

• Gastos mensuales: 300 $
• Edad: 27
• Valoración: 4,5.

Esta información tiene escalas diferentes y realizar el PCA utilizando esos datos conducirá a un resultado sesgado. Aquí es donde entra en juego la normalización de datos. Garantiza que cada atributo tenga el mismo nivel de contribución, para que una variable no domine a las demás. Para cada variable, la normalización se hace restando su media y dividiendo entre su desviación típica.   

Paso 2: matriz de covarianza

Como su nombre sugiere, este paso consiste en computar la matriz de covariables a partir de los datos normalizados. Se trata de una matriz simétrica, y cada elemento (i, j) corresponde a la covarianza entre las variables i y j.

Paso 3: vectores propios y valores propios

Geométricamente, un vector propio representa una dirección como "vertical" o "90 grados". Un valor propio es un número que representa la cantidad de varianza presente en los datos para una dirección determinada. Cada vector propio tiene su correspondiente valor propio. 

Paso 4: selección de los componentes principales

Hay tantos pares de vectores propios y valores propios como variables haya en los datos. En los datos con solo gastos mensuales, edad y valoración, habrá tres pares. No todos los pares son relevantes. Por tanto, el vector propio con el valor propio más alto corresponde al primer componente principal. El segundo componente principal es el vector propio con el segundo valor propio más alto, y así sucesivamente.

Paso 5: transformación de datos en nuevo espacio dimensional

Este paso consiste en reorientar los datos originales hacia un nuevo subespacio definido por los componentes principales Esta reorientación se realiza multiplicando los datos originales por los vectores propios calculados previamente.

Es importante recordar que esta transformación no modifica los datos originales en sí, sino que proporciona una nueva perspectiva para representar mejor los datos. 

Aplicaciones del análisis de componentes principales 

El análisis de componentes principales tiene diversas aplicaciones en nuestra vida cotidiana, como, por ejemplo, las finanzas, el procesamiento de imágenes, la sanidad y la seguridad.

Finanzas

Prever los precios de las acciones a partir de precios pasados es una noción utilizada en la investigación desde hace años. El PCA puede utilizarse para reducir la dimensionalidad y analizar los datos para ayudar a los expertos a encontrar componentes relevantes que expliquen la mayor parte de la variabilidad de los datos. Puedes obtener más información sobre la reducción de la dimensionalidad en R en nuestro curso específico. 

Procesamiento de imágenes

Una imagen está formada por varias características. El PCA se aplica principalmente en la compresión de imágenes para conservar los detalles esenciales de una imagen dada, reduciendo al mismo tiempo el número de dimensiones. Además, el PCA puede utilizarse para tareas más complicadas, como el reconocimiento de imágenes.   

Sanidad

En la misma lógica de la compresión de imágenes. El PCA se utiliza en la imagen por resonancia magnética (MRI) para reducir la dimensionalidad de las imágenes con el fin de mejorar la visualización y el análisis médico. También puede integrarse en tecnologías médicas utilizadas, por ejemplo, para reconocer una determinada enfermedad a partir de imágenes.

Seguridad

Los sistemas biométricos utilizados para el reconocimiento de huellas dactilares pueden integrar tecnologías que aprovechan el análisis de componentes principales para extraer las características más relevantes, como la textura de la huella dactilar e información adicional. 

Ejemplo real de PCA en R

Ahora que entiendes la teoría subyacente del PCA, estás preparado para verlo en acción.

Esta sección cubre todos los pasos, desde la instalación de los paquetes pertinentes, la carga y preparación de los datos aplicando el análisis de componentes principales en R, hasta la interpretación de los resultados. 

El código fuente está disponible en el espacio de trabajo de DataCamp.

Configuración del entorno 

Para realizar con éxito este tutorial, necesitarás las siguientes bibliotecas, y cada una de ellas requiere dos pasos principales para que puedas utilizarla con eficiencia: 

• Instala la biblioteca para acceder a todas las funciones.
• Carga para poder utilizar todas las funciones.

Paquete corrr en R

Se trata de un paquete de R para el análisis de correlaciones. Se centra principalmente en la creación y manejo de marcos de datos de R. A continuación se indican los pasos para instalar y cargar la biblioteca. 

install.packages("corrr")
library('corrr')

Paquete ggcorrplot en R

El paquete ggcorrplot proporciona varias funciones, pero no se limita a la función ggplot2, que facilita la visualización de la matriz de correlaciones. Igual que en las instrucciones anteriores, la instalación es sencilla.

install.packages("ggcorrplot")
library(ggcorrplot)

Paquete FactoMineR en R

Utilizado principalmente para el análisis exploratorio multivariante de datos; el paquete factoMineR da acceso al módulo PCA para realizar el análisis de componentes principales. 

install.packages("FactoMineR")
library("FactoMineR")

Paquete factoextra en R

Este último paquete proporciona todas las funciones pertinentes para visualizar los resultados del análisis de componentes principales. Estas funciones incluyen, por ejemplo, scree plot y biplot, por mencionar solo dos de las técnicas de visualización que se tratan más adelante en el artículo.

Exploración de los datos

Antes de cargar los datos y realizar cualquier otra exploración, es bueno comprender los datos con los que vas a trabajar y tener la información básica relacionada con ellos.  

Datos de proteínas

El conjunto de datos de proteínas es un conjunto de datos multivariante con valores reales que describen el consumo medio de proteínas de los ciudadanos de 25 países europeos. 

Para cada país hay diez columnas. Las ocho primeras corresponden a los distintos tipos de proteínas. La última corresponde al valor total de los valores medios de las proteínas.

Echemos un vistazo rápido a los datos. 

En primer lugar, cargamos los datos mediante la función read.csv() y, a continuación, str(), que da la imagen siguiente. 

protein_data <- read.csv("protein.csv")
str(protein_data)

Podemos ver que el conjunto de datos tiene 25 observaciones y 11 columnas, y todas las variables son numéricas, excepto la columna País, que es un texto. 

Descripción de los datos de proteínas

Comprobar valores nulos 

La presencia de valores que faltan puede sesgar el resultado del PCA. Por tanto, es muy recomendable aplicar el planteamiento adecuado para abordar esos valores.  Nuestro tutorial Las mejores técnicas para tratar los valores que faltan que todo científico de datos debe conocer puede ayudarte a tomar la decisión correcta. 

colSums(is.na(protein_data))

La función colSums() combinada con is.na() devuelve el número de valores que faltan en cada columna. Como podemos ver a continuación, en ninguna de las columnas faltan valores.

Número de valores que faltan en cada columna

Normalizar los datos

Como se indica al principio del artículo, el PCA solo funciona con valores numéricos. Por tanto, tenemos que deshacernos de la columna País. Además, la columna Total no es relevante para el análisis, ya que es la combinación lineal del resto de variables numéricas.

El código siguiente crea nuevos datos solo con columnas numéricas.

numerical_data <- protein_data[,2:10]

head(numerical_data)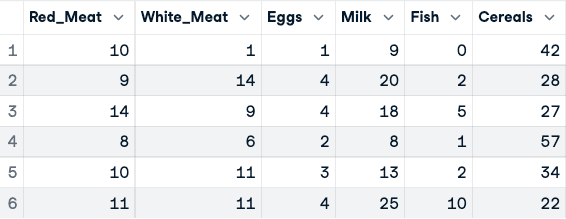

Antes de la normalización de los datos (solo se muestran las cinco primeras columnas)

Ahora se puede aplicar la normalización mediante la función scale(). 

data_normalized <- scale(numerical_data)
head(data_normalized)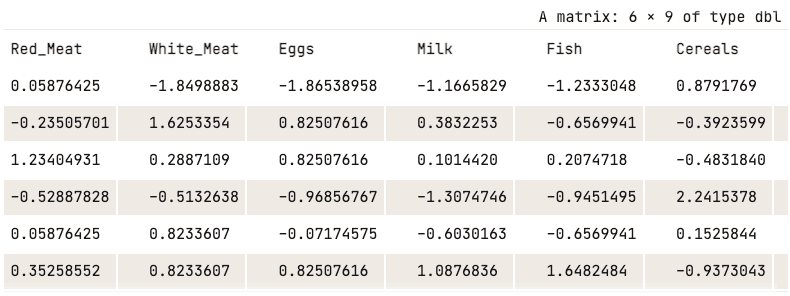

Datos normalizados (solo se muestran las cinco primeras columnas)

Calcular la matriz de correlaciones

Aunque en los cinco pasos anteriores se indique la matriz de covarianza, también puede utilizarse la correlación, que puede computarse utilizando la función cor() del paquete corrr. A continuación, se puede aplicar ggcorrplot() para una mejor visualización.

corr_matrix <- cor(data_normalized)
ggcorrplot(corr_matrix)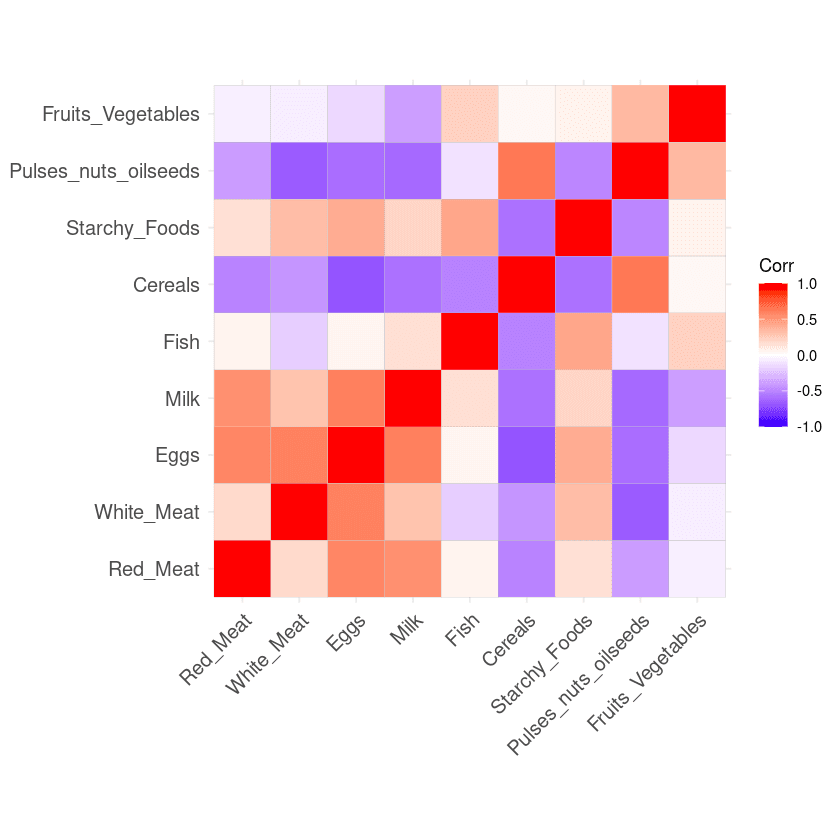

Matriz de correlación a partir de los datos

El resultado de la matriz de correlación puede interpretarse como sigue: 

• Cuanto mayor sea el valor, más positivamente correlacionadas están las dos variables.
• Cuanto más se acerque el valor a -1, más negativamente correlacionadas estarán.

Aplicación del PCA

Ahora, todos los recursos están disponibles para realizar el análisis PCA. En primer lugar, princomp() computa el PCA, y la función summary() muestra el resultado.

data.pca <- princomp(corr_matrix)
summary(data.pca)

Resumen de PCA de R 

En la captura de pantalla anterior, observamos que se han generado nueve componentes principales (de Comp.1 a Comp.9), que también se corresponden con el número de variables de los datos.

Cada componente explica un porcentaje de la varianza total del conjunto de datos. En la sección Proporción acumulada, el primer componente principal explica casi el 77 % de la varianza total. Esto implica que casi dos tercios de los datos del conjunto de 9 variables pueden representarse solo con el primer componente principal. El segundo explica el 12,08 % de la varianza total. 

La proporción acumulada de Comp.1 y Comp.2 explica casi el 89 % de la varianza total. Esto significa que los dos primeros componentes principales pueden representar con precisión los datos. 

Es estupendo tener los dos primeros componentes, pero ¿qué significan realmente? 

Esto puede responderse explorando cómo se relacionan con cada columna utilizando las cargas de cada componente principal. 

data.pca$loadings[, 1:2]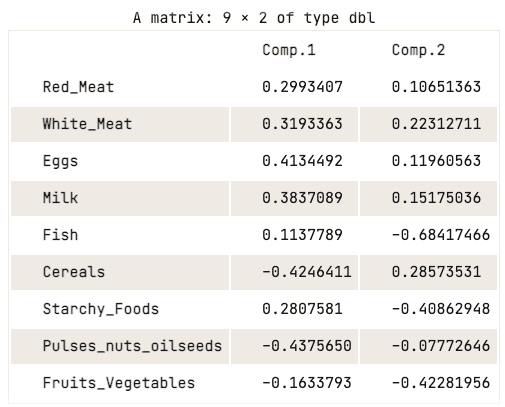

Matriz de carga de los dos primeros componentes principales

La matriz de carga muestra que el primer componente principal tiene valores positivos elevados tanto para la carne roja como para la carne blanca, los huevos y la leche. Sin embargo, los valores para cereales, legumbres, frutos secos y semillas oleaginosas y frutas y verduras son relativamente negativos. Esto sugiere que los países con una mayor ingesta de proteínas animales están en exceso, mientras que los países con una ingesta menor están en déficit.

En cuanto al segundo componente principal, presenta valores negativos elevados para el pescado, los alimentos almidonados y las frutas y verduras.  Esto implica que las dietas de los países subyacentes están muy influidas por su ubicación, como las regiones costeras para el pescado, y las regiones del interior para una dieta rica en verduras y patatas.

Visualización de los componentes principales 

El análisis anterior de la matriz de carga permitió comprender bien la relación entre cada uno de los dos primeros componentes principales y los atributos de los datos. Sin embargo, puede que no sea visualmente atractivo. 

Hay un par de estrategias de visualización estándar que pueden ayudar al usuario a obtener información de los datos, y el objetivo de esta sección es explicar algunos de esos enfoques, empezando por scree plot.  

Scree Plot

El primer enfoque de la lista es scree plot. Sirve para visualizar la importancia de cada componente principal y puede utilizarse para determinar el número de componentes principales que hay que conservar. El scree plot puede generarse utilizando la función fviz_eig(). 

fviz_eig(data.pca, addlabels = TRUE)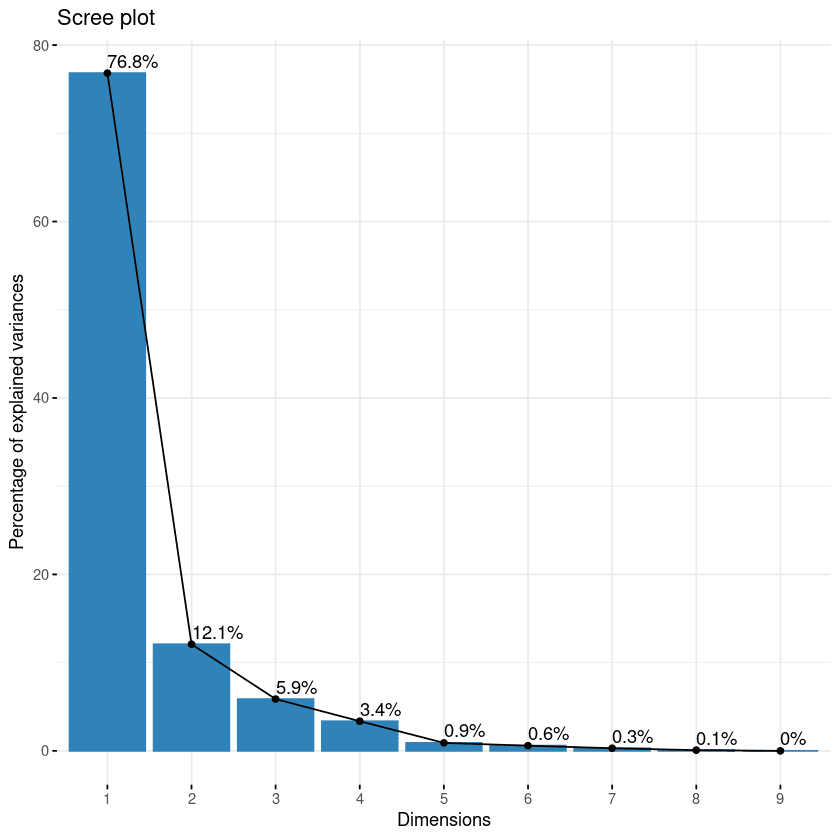

Scree plot de los componentes

Este plot muestra los valores propios en una curva descendente, de mayor a menor. Los dos primeros componentes pueden considerarse los más significativos, ya que contienen casi el 89 % de la información total de los datos.

Biplot de los atributos

Con el biplot, es posible visualizar las similitudes y desemejanzas de las muestras, y además muestra el impacto de cada atributo en cada uno de los componentes principales.

# Graph of the variables
fviz_pca_var(data.pca, col.var = "black")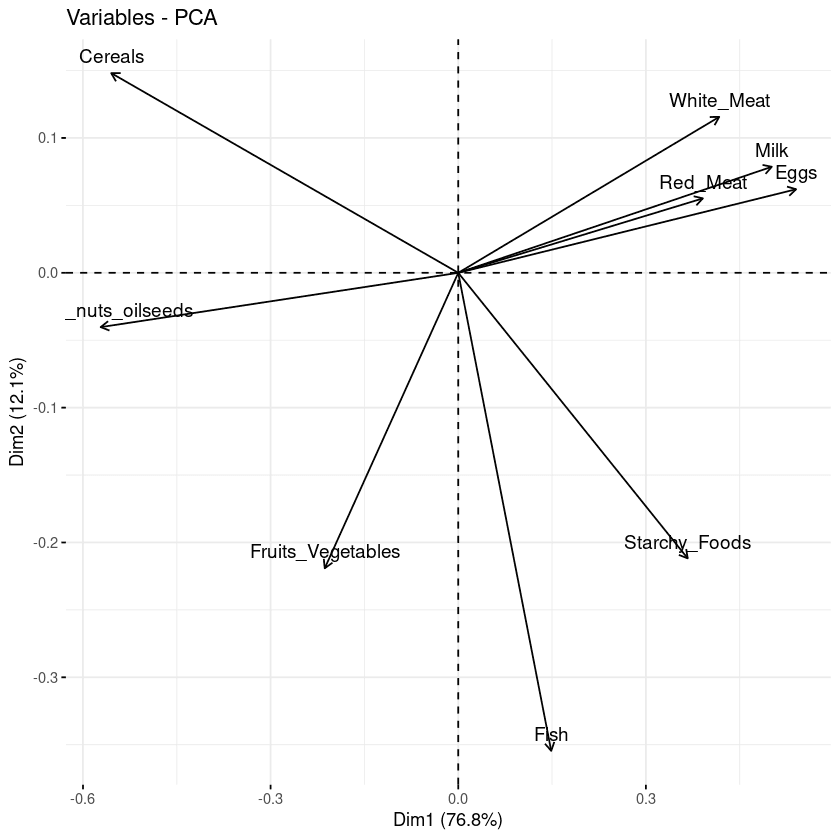

Biplot de las variables respecto a los componentes principales

En el plot anterior se pueden observar tres datos principales. 

• En primer lugar, todas las variables que se agrupan están correlacionadas positivamente entre sí, y ese es el caso, por ejemplo, de la carne blanca/roja, la leche y los huevos, que tienen una correlación positiva entre sí. Este resultado es sorprendente porque tienen los valores más altos en la matriz de carga con respecto al primer componente principal.
• Entonces, cuanto mayor sea la distancia entre la variable y el origen, mejor representada estará esa variable. En el biplot, los huevos, la leche y la carne blanca tienen mayor magnitud que la carne roja y, por tanto, están bien representados en comparación con esta.
• Por último, las variables correlacionadas negativamente se muestran a los lados opuestos del origen del biplot. 

Contribución de cada variable 

El objetivo de la tercera visualización es determinar en qué medida está representada cada variable en un componente determinado. Dicha calidad de representación se denomina Cos2, corresponde al coseno cuadrado y se computa con la función fviz_cos2.

• Un valor bajo significa que la variable no está perfectamente representada por ese componente. 
• En cambio, un valor alto significa una buena representación de la variable en ese componente.

fviz_cos2(data.pca, choice = "var", axes = 1:2)

El código anterior computa el valor del coseno cuadrado de cada variable con respecto a los dos primeros componentes principales. 

En la siguiente ilustración, los cereales, las semillas oleaginosas de frutos secos y legumbres, los huevos y la leche son las cuatro variables con el cos2 más alto, por lo que son las que más contribuyen a PC1 y PC2.

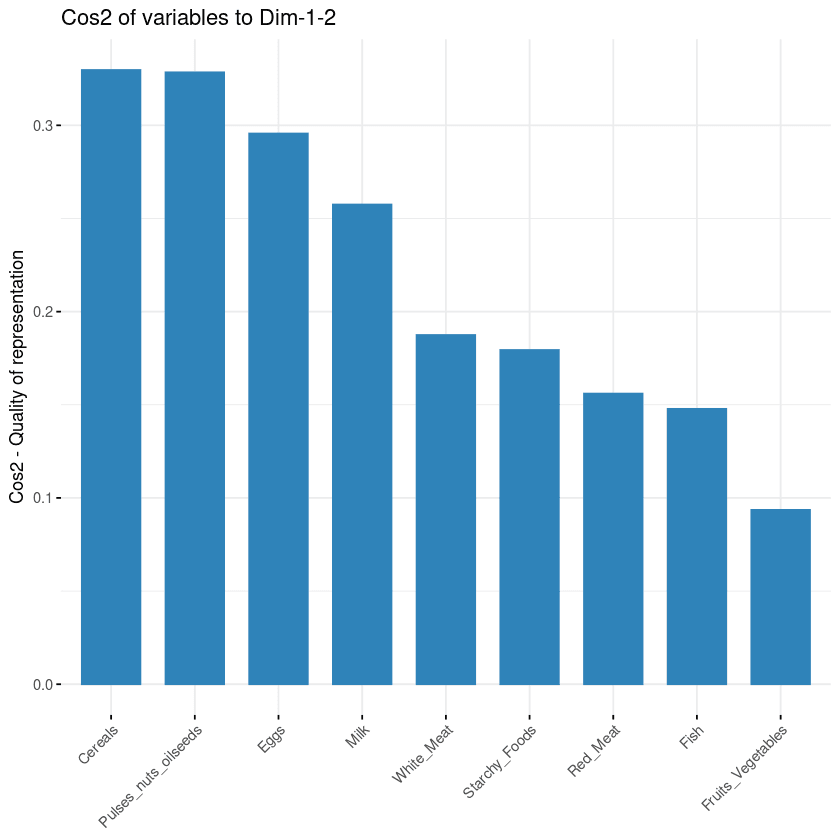
Contribución de las variables a los componentes principales

Biplot combinado con cos2 

Los dos últimos enfoques de visualización, biplot e importancia de los atributos, pueden combinarse para crear un único biplot, en el que los atributos con puntuaciones cos2 similares tendrán colores similares.  Esto se consigue ajustando la función fviz_pca_var del siguiente modo:  

fviz_pca_var(data.pca, col.var = "cos2",
            gradient.cols = c("black", "orange", "green"),
            repel = TRUE)

A partir del biplot siguiente:

• Los atributos de cos2 alto están coloreados en verde: Cereales, legumbres, semillas oleaginosas, huevos y leche.  
• Los atributos cos2 medios tienen color naranja: la carne blanca, los alimentos almidonados, el pescado y la carne roja.
• Por último, los atributos de cos2 bajo tienen color negro: frutas y verduras, 

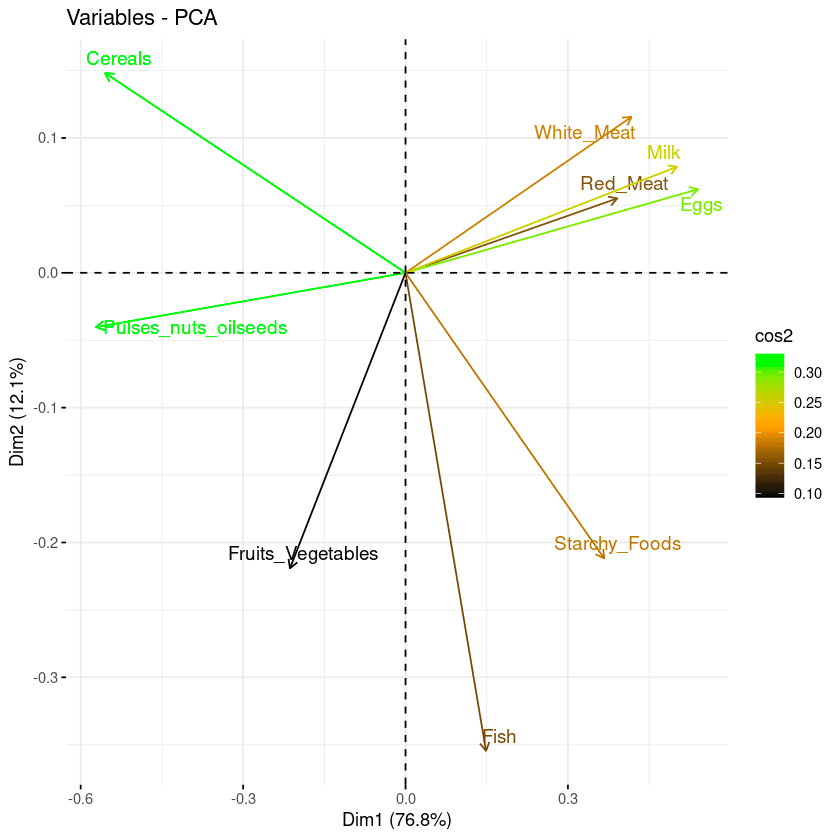
Combinación de biplot y puntuación cos2

Conclusión

En este artículo se ha tratado qué es el análisis de componentes principales y su importancia en el análisis de datos utilizando la matriz de correlación del paquete corrr. Además de cubrir algunas aplicaciones del mundo real, también te ha guiado a través de un ejemplo de PCA con diferentes estrategias de visualización, desde el uso de la función existente hasta su ajuste mediante la combinación de biplot y cos2 para una mejor comprensión y visualización de la relación entre el análisis pca en r y los atributos. 

Esperamos que te proporcione los conocimientos necesarios para visualizar y comprender con eficiencia la información oculta de tus datos.  

Para ampliar tu aprendizaje sobre el análisis de componentes principales, tienes el tutorial Análisis de componentes principales en Python. Ilustra el uso del PCA con Python en conjuntos de datos tabulares y de imagen. Nuestro curso Introducción a R es un buen paso siguiente para dominar los fundamentos del análisis de datos en R, lo que incluye vectores, listas y marcos de datos, y practicar con R con conjuntos de datos reales.