Saltar al contenido principal
InicioTutorialesAprendizaje automático

Tutorial sobre máquinas de vectores de soporte con Scikit-learn

En este tutorial, aprenderás sobre las máquinas de vectores de soporte, uno de los algoritmos de machine learning supervisado más populares y utilizados.
Actualizado mar 2024  · 15 min leer

SVM ofrece una exactitud muy alta en comparación con otros clasificadores, como la regresión logística y los árboles de decisión. Son conocidas por su truco del kernel para manejar espacios de entrada no lineales. Se utilizan en diversas aplicaciones, como la detección de caras, la detección de intrusos, la clasificación de correos electrónicos, artículos de noticias y páginas web, la clasificación de genes y el reconocimiento de escritura.

En este tutorial, utilizarás scikit-learn en Python. Si quieres saber más sobre este paquete de Python, te recomiendo que eches un vistazo a nuestro curso Aprendizaje supervisado con scikit-learn.

SVM es un algoritmo apasionante y los conceptos son relativamente sencillos. El clasificador separa los puntos de datos utilizando un hiperplano con el mayor margen. Por eso el clasificador SVM también se conoce como clasificador discriminativo. SVM encuentra un hiperplano óptimo que ayuda a clasificar nuevos puntos de datos.

En este tutorial, vas a tratar los siguientes temas:

Mira y aprende más sobre las máquinas de vectores de soporte con Scikit-learn en este vídeo de nuestro curso.

Máquinas de vectores de soporte

En general, las máquinas de vectores de soporte se consideran un enfoque de clasificación, pero pueden emplearse en problemas de clasificación y de regresión. Pueden manejar fácilmente varias variables continuas y categóricas. SVM crea un hiperplano en un espacio multidimensional para separar las distintas clases. SVM genera un hiperplano óptimo de forma iterativa, que se utiliza para minimizar un error. La idea central de SVM es hallar el hiperplano de máximo margen (MMH) que divida mejor el conjunto de datos en clases.

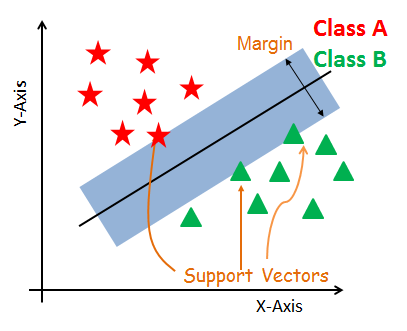
Vectores de soporte

Vectores de soporte

Los vectores de soporte son los puntos de datos más próximos al hiperplano. Estos puntos definirán mejor la línea de separación calculando los márgenes. Estos puntos son más relevantes para la creación del clasificador.

Hiperplano

Un hiperplano es un plano de decisión que separa un conjunto de objetos que pertenecen a diferentes clases.

Margen

Un margen es un espacio entre las dos líneas de los puntos de clase más cercanos. Se calcula como la distancia perpendicular de la línea a los vectores de soporte o puntos más cercanos. Si el margen es mayor entre las clases, se considera un buen margen; un margen menor es un mal margen.

¿Cómo funciona SVM?

El objetivo principal es segregar el conjunto de datos dado de la mejor manera posible. La distancia entre los puntos más cercanos se conoce como margen. El objetivo es seleccionar un hiperplano con el máximo margen posible entre vectores de soporte en el conjunto de datos dado. SVM busca el hiperplano de máximo margen en los pasos siguientes:

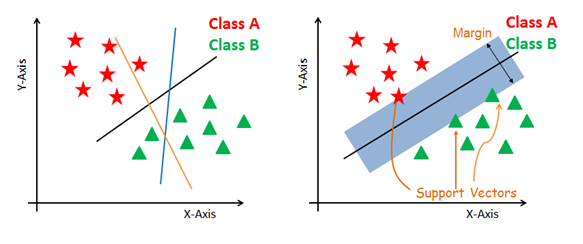
  1. Generar hiperplanos que segreguen las clases de la mejor manera. La figura de la izquierda muestra tres hiperplanos: negro, azul y naranja. Aquí, el azul y el naranja tienen mayor error de clasificación, pero el negro separa correctamente las dos clases.

  2. Selecciona el hiperplano con la máxima segregación de los puntos de datos más cercanos, como se muestra en la figura de la derecha.

Separador lineal

Tratar con planos no lineales e inseparables

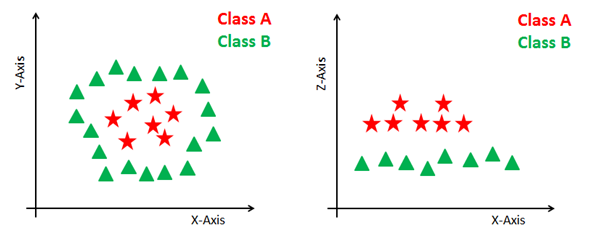
Algunos problemas no pueden resolverse utilizando el hiperplano lineal, como se muestra en la figura siguiente (lado izquierdo).

En tal situación, SVM utiliza un truco del kernel para transformar el espacio de entrada en un espacio de mayor dimensión, como se muestra a la derecha. Los puntos de datos se representan en el eje x y el eje z (Z es la suma al cuadrado de x e y: z = x^2 = y^2). Ahora puedes segregar fácilmente estos puntos utilizando la separación lineal.

Dimensión superior

Kernels SVM

El algoritmo SVM se implementa en la práctica utilizando un kernel. Un kernel transforma un espacio de datos de entrada en la forma requerida. SVM utiliza una técnica llamada truco del kernel. Aquí, el kernel toma un espacio de entrada de baja dimensión y lo transforma en un espacio de dimensión superior. En otras palabras, se puede decir que convierte el problema no separable en problemas separables añadiéndole más dimensión. Es útil sobre todo en problemas de separación no lineal. El truco del kernel te ayuda a crear un clasificador más exacto.

  • Kernel lineal Un kernel lineal puede utilizarse como producto escalar normal de dos observaciones cualesquiera. El producto entre dos vectores es la suma de la multiplicación de cada par de valores de entrada.
K(x, xi) = sum(x * xi)
  • Kernel polinómico Un kernel polinómico es una forma más generalizada del kernel lineal. El kernel polinómico puede distinguir espacio de entrada curvo o no lineal.
K(x,xi) = 1 + sum(x * xi)^d

Donde d es el grado del polinomio. d = 1 es similar a la transformación lineal. El grado debe especificarse manualmente en el algoritmo de aprendizaje.

  • Kernel de función de base radial El kernel de función de base radial es una popular función de kernel que se utiliza habitualmente en la clasificación de máquinas de vectores de soporte. RBF puede mapear un espacio de entrada en un espacio de dimensión infinita.
K(x,xi) = exp(-gamma * sum((x – xi^2))

Aquí gamma es un parámetro, que va de 0 a 1. Un valor más alto de gamma se ajustará perfectamente al conjunto de datos de entrenamiento, lo que provoca un sobreajuste. Gamma = 0,1 se considera un buen valor por defecto. El valor de gamma debe especificarse manualmente en el algoritmo de aprendizaje.

Creación de clasificadores en Scikit-learn

Hasta ahora, has conocido los fundamentos teóricos de SVM. Ahora conocerás su implementación en Python utilizando scikit-learn.

En la parte de creación del modelo, puedes utilizar el conjunto de datos sobre el cáncer, que es un problema de clasificación multiclase muy famoso. Este conjunto de datos se calcula a partir de una imagen digitalizada de una aspiración con aguja fina (FNA) de una masa mamaria. Describen las características de los núcleos celulares presentes en la imagen.

El conjunto de datos comprende 30 características (radio medio, textura media, perímetro medio, área media, suavidad media, compactibilidad media, concavidad media, puntos cóncavos medios, simetría media, dimensión fractal media, error de radio, error de textura, error de perímetro, error de área, error de suavidad, error de compactibilidad, error de concavidad, error de puntos cóncavos, error de simetría, error de dimensión fractal, peor radio, peor textura, peor perímetro, peor área, peor suavidad, peor compactibilidad, peor concavidad, peores puntos cóncavos, peor simetría y peor dimensión fractal) y un objetivo (tipo de cáncer).

Estos datos tienen dos tipos de clases de cáncer: maligno (dañino) y benigno (no dañino). Aquí puedes crear un modelo para clasificar el tipo de cáncer. El conjunto de datos está disponible en la biblioteca scikit-learn o puedes descargarlo de UCI Machine Learning Library.

Run and edit the code from this tutorial online

Run Code

Cargar los datos

Primero carguemos el conjunto de datos que vas a utilizar.

#Import scikit-learn dataset library
from sklearn import datasets

#Load dataset
cancer = datasets.load_breast_cancer()

Explorar los datos

Después de cargar el conjunto de datos, quizá quieras saber algo más sobre él. Puedes comprobar los nombres de las características y los objetivos.

# print the names of the 13 features
print("Features: ", cancer.feature_names)

# print the label type of cancer('malignant' 'benign')
print("Labels: ", cancer.target_names)

Features:  ['mean radius' 'mean texture' 'mean perimeter' 'mean area'
 'mean smoothness' 'mean compactness' 'mean concavity'
 'mean concave points' 'mean symmetry' 'mean fractal dimension'
 'radius error' 'texture error' 'perimeter error' 'area error'
 'smoothness error' 'compactness error' 'concavity error'
 'concave points error' 'symmetry error' 'fractal dimension error'
 'worst radius' 'worst texture' 'worst perimeter' 'worst area'
 'worst smoothness' 'worst compactness' 'worst concavity'
 'worst concave points' 'worst symmetry' 'worst fractal dimension']
Labels:  ['malignant' 'benign']

Explorémoslo un poco más. También puedes comprobar la forma del conjunto de datos utilizando shape.

# print data(feature)shape
cancer.data.shape

(569, 30)

Comprobemos los 5 mejores registros del conjunto de características.

# print the cancer data features (top 5 records)
print(cancer.data[0:5])

[[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
  1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
  6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
  1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
  4.601e-01 1.189e-01]
 [2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
  7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
  5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
  2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
  2.750e-01 8.902e-02]
 [1.969e+01 2.125e+01 1.300e+02 1.203e+03 1.096e-01 1.599e-01 1.974e-01
  1.279e-01 2.069e-01 5.999e-02 7.456e-01 7.869e-01 4.585e+00 9.403e+01
  6.150e-03 4.006e-02 3.832e-02 2.058e-02 2.250e-02 4.571e-03 2.357e+01
  2.553e+01 1.525e+02 1.709e+03 1.444e-01 4.245e-01 4.504e-01 2.430e-01
  3.613e-01 8.758e-02]
 [1.142e+01 2.038e+01 7.758e+01 3.861e+02 1.425e-01 2.839e-01 2.414e-01
  1.052e-01 2.597e-01 9.744e-02 4.956e-01 1.156e+00 3.445e+00 2.723e+01
  9.110e-03 7.458e-02 5.661e-02 1.867e-02 5.963e-02 9.208e-03 1.491e+01
  2.650e+01 9.887e+01 5.677e+02 2.098e-01 8.663e-01 6.869e-01 2.575e-01
  6.638e-01 1.730e-01]
 [2.029e+01 1.434e+01 1.351e+02 1.297e+03 1.003e-01 1.328e-01 1.980e-01
  1.043e-01 1.809e-01 5.883e-02 7.572e-01 7.813e-01 5.438e+00 9.444e+01
  1.149e-02 2.461e-02 5.688e-02 1.885e-02 1.756e-02 5.115e-03 2.254e+01
  1.667e+01 1.522e+02 1.575e+03 1.374e-01 2.050e-01 4.000e-01 1.625e-01
  2.364e-01 7.678e-02]]

Echemos un vistazo al conjunto de objetivos.

# print the cancer labels (0:malignant, 1:benign)
print(cancer.target)

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 1 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 0 1 0 0
 1 0 1 0 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1
 1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 0 1 1 1 1 0 1
 1 1 1 1 1 1 1 1 0 1 1 1 1 0 0 1 0 1 1 0 0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 1 0
 1 0 1 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 1 1
 1 0 1 1 1 1 1 0 0 1 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 0 0 0 1 1
 1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0
 0 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1
 1 0 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 1 1
 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1
 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 0 1 0 0
 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 0 0 0 0 0 0 1]

Dividir los datos

Para comprender el rendimiento del modelo, dividir el conjunto de datos en un conjunto de entrenamiento y un conjunto de prueba es una buena estrategia.

Divide el conjunto de datos utilizando la función train_test_split(). Debes pasar 3 parámetros: features, target y test_set size. Además, puedes utilizar random_state para seleccionar registros aleatoriamente.

# Import train_test_split function
from sklearn.model_selection import train_test_split

# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, test_size=0.3,random_state=109) # 70% training and 30% test

Generar el modelo

Vamos a crear un modelo de máquina de vectores de soporte. En primer lugar, importa el módulo SVM y crea el objeto clasificador de vectores de soporte pasando el argumento kernel como kernel lineal en la función SVC().

A continuación, ajusta tu modelo al conjunto de entrenamiento utilizando fit() y realiza la previsión en el conjunto de prueba utilizando predict().

#Import svm model
from sklearn import svm

#Create a svm Classifier
clf = svm.SVC(kernel='linear') # Linear Kernel

#Train the model using the training sets
clf.fit(X_train, y_train)

#Predict the response for test dataset
y_pred = clf.predict(X_test)

Evaluar el modelo

Estimemos la exactitud con la que el clasificador o modelo puede prever el cáncer de mama de los pacientes.

La precisión puede calcularse comparando los valores reales del conjunto de prueba y los valores previstos.

#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics

# Model Accuracy: how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

Accuracy: 0.9649122807017544

Has obtenido un índice de clasificación del 96,49 %, que se considera una exactitud muy buena.

Para una evaluación más detallada, también puedes comprobar la precisión y el recuerdo del modelo.

# Model Precision: what percentage of positive tuples are labeled as such?
print("Precision:",metrics.precision_score(y_test, y_pred))

# Model Recall: what percentage of positive tuples are labelled as such?
print("Recall:",metrics.recall_score(y_test, y_pred))

Precision: 0.9811320754716981
Recall: 0.9629629629629629

Has obtenido una precisión del 98 % y un recuerdo del 96 %, que se consideran valores muy buenos.

Ajuste de hiperparámetros

  • Kernel: La función principal del kernel es transformar los datos de entrada del conjunto de datos dado en la forma requerida. Hay diferentes tipos de funciones, como la lineal, la polinómica y la función de base radial (RBF). El polinomio y la RBF son útiles para el hiperplano no lineal. Los kernels polinómicos y de RBF calculan la línea de separación en la dimensión superior. En algunas de las aplicaciones, se sugiere utilizar un kernel más complejo para separar las clases que son curvas o no lineales. Esta transformación puede dar lugar a clasificadores más exactos.
  • Regularización: Parámetro de regularización en parámetro C de Scikit-learn de python utilizado para mantener la regularización. Aquí C es el parámetro de penalización, que representa clasificación errónea o término de error. La clasificación errónea o el término de error indica a la optimización SVM cuánto error es soportable. Así puedes controlar la compensación entre el límite de decisión y el término de clasificación errónea. Un valor menor de C crea un hiperplano de margen pequeño y un valor mayor de C crea un hiperplano de margen mayor.
  • Gamma: Un valor menor de gamma se ajustará holgadamente al conjunto de datos de entrenamiento, mientras que un valor mayor de gamma se ajustará de forma exacta al conjunto de datos de entrenamiento, lo que provoca sobreajuste. En otras palabras, se puede decir que un valor bajo de gamma solo tiene en cuenta los puntos cercanos al calcular la línea de separación, mientras que un valor a de gamma tiene en cuenta todos los puntos de datos en el cálculo de la línea de separación.

Ventajas

Los clasificadores SVM ofrecen una buena exactitud y realizan previsiones más rápidas que el algoritmo Ingenuo Bayes. También utilizan menos memoria porque emplean un subconjunto de puntos de entrenamiento en la fase de decisión. SVM funciona bien con un margen claro de separación y con un espacio de alta dimensión.

Desventajas

SVM no es adecuada para grandes conjuntos de datos debido a su elevado tiempo de entrenamiento y, además, tarda más tiempo en entrenarse que Ingenuo Bayes. Funciona mal con clases solapadas y también es sensible al tipo de kernel utilizado.

Conclusión

Enhorabuena, ¡has llegado al final de este tutorial!

En este tutorial, has abarcado mucho sobre el algoritmo de máquina de vectores de soporte, su funcionamiento, los kernels, el ajuste de hiperparámetros, la creación de modelos y la evaluación en el conjunto de datos del cáncer de mama utilizando el paquete Scikit-learn. También has visto sus ventajas e inconvenientes. Espero que hayas aprendido algo valioso.

Para saber más sobre este tipo de clasificadores, deberías echar un vistazo a nuestro curso Clasificadores lineales en Python. Este curso presenta otros tipos de funciones de regresión y pérdida, así como las máquinas de vectores de soporte.

Espero tus comentarios o preguntas. Para hacer preguntas, puedes dejar un comentario: intentaré responder lo mejor que pueda.

Temas
Aprendizaje automático
Ciencia de datos
Python

Cursos de Scikit-learn

Course

Supervised Learning with scikit-learn

4 hr
111.9K
Grow your machine learning skills with scikit-learn in Python. Use real-world datasets in this interactive course and learn how to make powerful predictions!
See DetailsRight Arrow
Start Course
Ver másRight Arrow
Relacionado

tutorial

Programación orientada a objetos (POO) en Python: Tutorial

Aborda los fundamentos de la Programación Orientada a Objetos (POO) en Python: explora las clases, los objetos, los métodos de instancia, los atributos y ¡mucho más!
Théo Vanderheyden's photo

Théo Vanderheyden

12 min

tutorial

Cómo comentar un bloque de código en Python

Utilizar comentarios es fundamental para trabajar eficazmente con Python. En este breve tutorial, aprenderás a comentar un bloque de código en Python.
Adel Nehme's photo

Adel Nehme

3 min

tutorial

Guía completa de programación de sockets en Python

Aprende los fundamentos de la programación de sockets en Python
Serhii Orlivskyi's photo

Serhii Orlivskyi

41 min

tutorial

Tutorial de Python: Streamlit

Este tutorial sobre Streamlit está pensado para ayudar a los científicos de datos o ingenieros de machine learning que no son desarrolladores web y no están interesados en pasar semanas aprendiendo a utilizar estos marcos para crear aplicaciones web.
Nadia mhadhbi's photo

Nadia mhadhbi

18 min

tutorial

Tutorial de Pandas: DataFrames en Python

Explora el análisis de datos con Python. Los DataFrames de Pandas facilitan la manipulación de tus datos, desde la selección o sustitución de columnas e índices hasta la remodelación de tus datos.
Karlijn Willems's photo

Karlijn Willems

20 min

tutorial

Explicación de las funciones de pérdida en el machine learning

Explora el papel crucial de las funciones de pérdida en el machine learning con nuestra completa guía. Comprende la diferencia entre funciones de pérdida y de coste, profundiza en varios tipos como MSE y MAE, y aprende sus aplicaciones en tareas de ML.
Richmond Alake's photo

Richmond Alake

20 min

See MoreSee More