SymPy: Guía completa de matemáticas simbólicas en Python

Si alguna vez has querido que Python realice y exprese operaciones algebraicas como un matemático, SymPy es la respuesta.

SymPy significa Symbolic Python (Python simbólico) y es una biblioteca creada para realizar cálculos simbólicos, lo que significa que puede expandir, simplificar, diferenciar y resolver ecuaciones simbólicamente, tal y como lo harías en papel.  Una extensión importante es que las expresiones matemáticas con variables no evaluadas se dejan en forma simbólica. Por ejemplo, la raíz cuadrada de ocho se representará como 2*sqrt(2), en lugar de aproximarla a 2,828.   

Algunas de las principales ventajas de SymPy son que es de código abierto, está escrito completamente en Python y ofrece compatibilidad con otras bibliotecas de Python. 

Principales ventajas de Sympy. Fuente: Imagen de Napkin AI

Breve historia de SymPy

SymPy comenzó con una idea sencilla: hacer que el cálculo simbólico fuera accesible para todos.

Fue fundada en 2006 por Ondřej Čertík, un estudiante de la Universidad de Nevada. Quería crear una biblioteca matemática simbólica ligera y flexible en Python puro para que la gente no tuviera que lidiar con las complejidades de los grandes sistemas de álgebra computacional como Maple o Mathematica. 

Entre 2007 y 2010, SymPy creció rápidamente al participar en Google Summer of Code, durante el cual se ampliaron significativamente los principales módulos básicos, como la simplificación, la resolución y el cálculo. 

Hacia 2012, SymPy había madurado hasta tal punto que se integró en SageMath, lo que supuso su reconocimiento como un backend simbólico fiable dentro del amplio ecosistema científico de Python. A día de hoy, SymPy ha evolucionado más allá de su uso en álgebra hacia ámbitos avanzados como la física, la geometría, la combinatoria, la generación de código y las herramientas de compilación orientadas al rendimiento.

Introducción a SymPy

Antes de explorar la magia de SymPy, vamos a configurarlo correctamente.

Instalación y configuración

La forma más fácil de instalar SymPy, que también es el método recomendado, es utilizando pip:

pip install sympy

Si utilizas Conda, el comando es:

conda install sympy

También puedes instalar directamente desde el código fuente (útil para colaboradores):

git clone https://github.com/sympy/sympy.git

Si te preguntas sobre las dependencias: SymPy se ejecuta íntegramente en Python y no depende de bibliotecas externas. Se pueden instalar paquetes opcionales como mpmath para realizar operaciones aritméticas de precisión arbitraria:

pip install mpmath

Verificación de la instalación

Para confirmar la instalación, abre Python y escribe:

import sympy
print(sympy.__version__)

1.14.0

La salida muestra la versión instalada del paquete.  Ahora puedes probar el paquete con una expresión simple:

from sympy import symbols

# Define x as a symbolic variable
x = symbols('x')

print((x + 2)**2)

(x + 2)**2

En cuanto a la resolución de problemas:

• Si ves « ModuleNotFoundError », vuelve a ejecutar « pip install sympy ».

• En caso de conflictos de versiones, actualiza pip: pip install --upgrade pip

Además, es bueno saber que: Si crees que hay un error o deseas solicitar una función, también puedes abrirun ticket de incidencia en. Para obtener información detallada sobre los métodos de instalación, consulta la documentación oficial.

Uso básico

SymPy proporciona un entorno interactivo en el que puedes manipular expresiones algebraicas de forma simbólica.

from sympy import symbols, expand

#define x and y as symbolic variables
x, y = symbols('x y')

# create an algebraic expression
expr = (x + y)**2

expanded = expand(expr)
print(expanded)

x**2 + 2*x*y + y**2

El resultado impreso arriba x**2 + 2*x*y + y**2 es la forma completamente expandida, que demuestra cómo SymPy realiza álgebra simbólica exacta en lugar de cálculos numéricos.

Características y funcionalidades principales

Las funcionalidades principales se basan en el cálculo simbólico, lo que significa trabajar con funciones, ecuaciones y expresiones como símbolos en lugar de números.

Operaciones aritméticas

Puedes tratar las variables simbólicas como si fueran algebraicas. Además, las funciones pueden pasar de un formulario a otro, como se muestra en el código siguiente. 

Mediante el uso de expand() para la distribución y factor() para la simplificación inversa, SymPy transforma entre formas expandidas y factorizadas de una expresión algebraica.

from sympy import symbols, expand, factor

# Define symbolic variables x and y
x, y = symbols('x y')

# Create an algebraic expression
expr = (x + y)**2

# Expand the expression to its full polynomial form
print(expand(expr))  

# Factor the expanded polynomial back into its compact form
print(factor(x**2 + 2*x*y + y**2)) 

x**2 + 2*x*y + y**2
(x + y)**2

Técnicas de simplificación

La simplificación es fundamental para el cálculo simbólico. En Sympy hay una función general, llamada « simplify() » (simplificar), que se utiliza para simplificar fácilmente expresiones racionales, trigonométricas o algebraicas.

from sympy import simplify, trigsimp, sin, cos

# Create a trigonometric expression
expr = sin(x)**2 + cos(x)**2

# General simplification — recognizes that sin²x + cos²x = 1
print(simplify(expr)) 

# Trigonometric-specific simplification — also simplifies to 1
print(trigsimp(expr)) 

El resultado de las funciones « simplify() » y « trigsimp() » anteriores es uno. 

Operaciones de cálculo

SymPy es ideal para el cálculo porque te permite realizar derivadas, integrales, límites e incluso expansiones en serie de forma simbólica, igual que si lo hicieras a mano, pero con una precisión perfecta.

Diferenciación

Para calcular derivadas, utiliza la función diff().

from sympy import diff

# Define a symbolic polynomial expression
f = x**3 + 2*x**2 + x

# Compute the derivative of the expression with respect to x
df = diff(f, x)
print(df)

3*x**2 + 4*x + 1

Integración

El siguiente código calcula la integral indefinida de la expresión simbólica f con respecto a la variable x utilizando la función integrate() de SymPy. A continuación, se imprime la antiderivada resultante.

from sympy import integrate

# Compute the indefinite integral of the expression f with respect to x
integral = integrate(f, x)
print(integral)

x**4/4 + 2*x**3/3 + x**2/2

Límites

El cálculo del límite es una operación de cálculo clásico, que se puede realizar utilizando la función limit() de SymPy. La sintaxis es: limit(f(x), x, x0).  Por ejemplo, el código siguiente calcula el límite de la expresión sin(x)/x cuando x tiende a cero e imprime el resultado exacto, one. 

from sympy import limit, sin

# Compute the limit of sin(x)/x as x approaches 0 
limit_expr = limit(sin(x)/x, x, 0)
print(limit_expr) 

Expansión de series

La función series() se puede utilizar para calcular la expansión de Taylor o la serie de potencias de una expresión matemática alrededor de un punto especificado.

from sympy import series, exp

# Generate the Taylor series expansion of e^x around 0 up to 5 terms
print(series(exp(x), x, 0, 5))

1 + x + x**2/2 + x**3/6 + x**4/24 + O(x**5)

Resúmenes

La función summation() en SymPy realiza una suma simbólica exacta en un rango determinado, igual que la notación sigma en matemáticas.

from sympy import summation, symbols

# Compute the symbolic sum of 1/n^2 from n = 1 to 5
n = symbols('n')
print(summation(1/n**2, (n, 1, 5)))  

5269/3600

Resolver ecuaciones

SymPy facilita la resolución de ecuaciones simbólicas, no solo las algebraicas simples, sino también sistemas de ecuaciones, ecuaciones diferenciales e incluso ecuaciones diofánticas, que solo tienen números enteros como soluciones. 

Cuenta con potentes solucionadores como 

• solve() para ecuaciones algebraicas, 

• linsolve() para sistemas lineales, y 

• dsolve() para ecuaciones diferenciales que dan soluciones exactas siempre que sea posible. 

Ecuaciones algebraicas

from sympy import Eq, solve
# Define and solve the equation x^2 - 4 = 0 symbolically
eq = Eq(x**2 - 4, 0)

print(solve(eq, x)) 

[-2, 2]

Sistemas de ecuaciones

from sympy import linsolve, symbols

# Solve a system of linear equations:
# x + y = 5  and  x - y = 1
x, y = symbols('x y')
sol = linsolve([x + y - 5, x - y - 1], (x, y))

print(sol) # Outputs the solution as a set (x, y)

{(3, 2)}

Ecuaciones diferenciales

from sympy import Function, dsolve

# Define y as a symbolic function of x
y = Function('y')

# Define a second-order differential equation
diff_eq = Eq(y(x).diff(x, 2) - y(x), 0)

# Solve the differential equation symbolically
print(dsolve(diff_eq))

Eq(y(x), C1*exp(-x) + C2*exp(x))

Operaciones matriciales

SymPy es una herramienta excelente para el álgebra lineal, ya que admite matrices simbólicas. Puedes trabajar fácilmente con matrices y realizar operaciones matemáticas como sumas y multiplicaciones, tal y como lo harías en álgebra convencional. 

from sympy import Matrix

# Define symbolic matrices A and B
A = Matrix([[1, 2], [x, 3]])
B = Matrix([[x], [4]])

# Perform matrix multiplication
print(A * B)

Matrix([[x + 8], [x**2 + 12]])

Operaciones avanzadas

SymPy también te permite calcular propiedades importantes de las matrices, como determinantes, inversas, valores propios y vectores propios de forma simbólica, proporcionándote respuestas exactas. 

# Compute the determinant of matrix A
A.det()      

# Compute the inverse of matrix A
A.inv()      

# Compute the eigenvalues of matrix A
A.eigenvals() 

{2 - sqrt(2*x + 1): 1, sqrt(2*x + 1) + 2: 1}

Capacidades de gráficando

SymPy no se limita al cálculo simbólico, sino que también permite visualizar expresiones matemáticas. Con las utilidades de gráficando integradas, puedes generar gráficos en 2D e incluso en 3D de funciones simbólicas con pocas líneas de código. 

Por ejemplo, el código siguiente genera un gráfico 2D:  

from sympy.plotting import plot


# Plot the function x^2 over the range -5 to 5
plot(x**2, (x, -5, 5))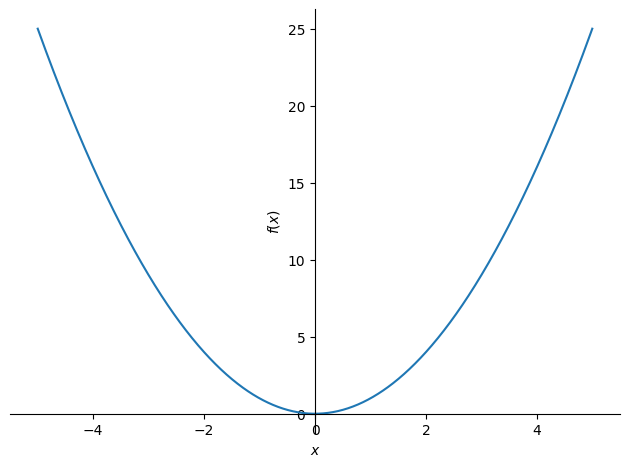

Gráfico 2D generado con SymPy. 

Para generar gráficos 3D, puedes utilizar la función « plot3d() », como se muestra a continuación.

from sympy.plotting import plot3d
from sympy import sin

# Generate a 3D surface plot of the function sin(x*y) over the specified x and y ranges
plot3d(sin(x*y), (x, -5, 5), (y, -5, 5))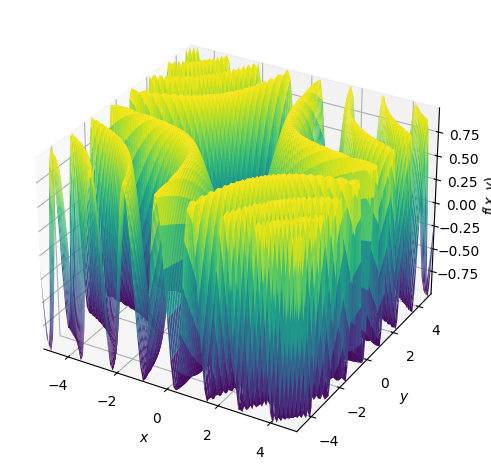

Capacidad de gráficando 3D de SymPy

Y si necesitas más control o estilo, SymPy también se puede integrar con Matplotlib para permitir visualizaciones totalmente personalizables. Para obtener visualizaciones más avanzadas, lee nuestro tutorial sobre Plotly Shapes.

Funciones avanzadas

SymPy va mucho más allá del álgebra básica: se extiende a los polinomios, la combinatoria e incluso la física.

Manipulación de polinomios

Puedes definir y manipular polinomios fácilmente. El código siguiente crea un objeto polinómico a partir de la expresión y, a continuación, imprime su grado y su forma factorizada con coeficientes utilizando la función ` Poly() ` de SymPy. 

from sympy import Poly

# Create a symbolic polynomial in variable x
p = Poly(x**3 - 3*x**2 + x - 3, x)

# Print the degree of the polynomial (highest power of x)
print(p.degree())  

# Print the factorized form of the polynomial along with coefficients
print(p.factor_list())  

3
(1, [(Poly(x - 3, x, domain='ZZ'), 1), (Poly(x**2 + 1, x, domain='ZZ'), 1)])

Para sistemas polinómicos complejos, se admiten bases de Gröbner, que son una versión simplificada y estandarizada de un sistema de ecuaciones polinómicas, lo que facilita su resolución. 

Por ejemplo, el código siguiente calcula la base de Gröbner para el sistema polinómico [x*y - 1, y - x], lo que significa que reescribe las ecuaciones en una forma más simple y estructurada que es más fácil de resolver. El resultado muestra que el sistema es equivalente a las ecuaciones más claras x = y y y² = 1, que ahora pueden resolverse directamente.

from sympy import groebner, symbols

# Define x and y as symbolic variables
x, y = symbols('x y')

# Compute the Gröbner basis for the system of polynomial equations
print(groebner([x*y - 1, y - x], x, y))

GroebnerBasis([x - y, y**2 - 1], x, y, domain='ZZ', order='lex')

Combinatoria, matemáticas discretas y teoría de números.

SymPy cuenta con varias utilidades que te permiten manejar problemas combinatorios y de teoría de números. 

Por ejemplo, en el siguiente código:

• La función binomial(5, 2) calcula el número de formas de elegir 2 elementos de entre 5 (un problema de combinación). 

• factorial(6) calcula 6!, una operación habitual en las permutaciones. 

• isprime(19) comprueba si 19 es un número primo, y 

• factorint(100) devuelve tu factorización prima exacta como un {2: 2, 5: 2}. 

from sympy import binomial, factorial, isprime, factorint
print(binomial(5, 2))   # 10
print(factorial(6))     # 720
print(isprime(19))      # True
print(factorint(100))   # {2: 2, 5: 2}

10
720
True
{2: 2, 5: 2}

10
720
True
{2: 2, 5: 2}

En conjunto, estas funciones ilustran cómo SymPy maneja las matemáticas discretas con facilidad y precisión. También puedes trabajar directamente con particiones, permutaciones y combinaciones.

Aplicaciones de geometría y física

SymPy no solo está pensado para el álgebra y el cálculo, sino que también ofrece módulos especiales para geometría y física. 

En el módulo de geometría, puedes definir objetos matemáticos como puntos, líneas, círculos y polígonos. Mediante el uso de símbolos, también puedes obtener ecuaciones de rectas, intersecciones, distancias y puntos medios. 

Por ejemplo, para crear dos puntos y dibujar una línea entre ellos, haz lo siguiente:

from sympy import Point, Line, Circle

# Define two points and create a line passing through them
A, B = Point(0, 0), Point(1, 1)
L = Line(A, B)

# Print the symbolic equation of the line
print(L.equation())  

-x + y

Además de sus capacidades geométricas, SymPy ofrece un módulo de física muy útil. Con este módulo, puedes modelar mecánica clásica, sistemas cuánticos, unidades y tamaños.  Esto es así tanto si utilizas metros por segundo para calcular la velocidad como si resuelves ecuaciones de movimiento con símbolos. 

from sympy.physics.units import meter, second

# Define a symbolic physical quantity: velocity = 10 meters per second
velocity = 10 * meter / second
print(velocity)

10*meter/second

Impresión y salida LaTeX

SymPy te permite imprimir expresiones simbólicas en múltiples formatos, entre los que se incluyen:

• Impresión atractiva y fácil de leer 
• Salida basada en Unicode, y 
• LaTeX, que es el lenguaje de formato estándar utilizado en artículos de investigación y documentación científica. 

Puedes utilizar funciones como pprint() para que tus ecuaciones tengan un aspecto limpio y profesional en un cuaderno Jupyter o al elaborar un informe. Incluso puedes utilizar latex() para prepararlos para un trabajo de investigación. Te ahorra la molestia de tener que formatear todo tú mismo.

from sympy import pprint, latex, symbols

# Define x and y as symbolic variables
x, y = symbols('x y')

# Now you can perform symbolic math operations
expr = (x+y)**3

# Pretty print to the console
pprint(expr)

# Print the LaTeX string
print(latex(expr))

     3
(x + y) 
\left(x + y\right)^{3}

Generación de código y optimización del rendimiento

Aunque SymPy destaca en el cálculo simbólico, también permite convertir expresiones simbólicas en código ejecutable optimizado para un uso numérico de alto rendimiento.

El código siguiente utiliza la utilidad « codegen() » (Convertir en código C) de SymPy para generar automáticamente código en lenguaje C a partir de una expresión simbólica, dejándolo listo para su uso en aplicaciones integradas.

from sympy.utilities.codegen import codegen

# Generate C code for the symbolic function and save it as 'output'
codegen(("f", x**2 + 1), "C", "output")

[('output.c',
  '/******************************************************************************\n *                      Code generated with SymPy 1.14.0                      *\n *                                                                            *\n *              See http://www.sympy.org/ for more information.               *\n *                                                                            *\n *                       This file is part of \'project\'                       *\n ******************************************************************************/\n#include "output.h"\n#include <math.h>\n\ndouble f(double x) {\n\n   double f_result;\n   f_result = pow(x, 2) + 1;\n   return f_result;\n\n}\n'),
 ('output.h',
  "/******************************************************************************\n *                      Code generated with SymPy 1.14.0                      *\n *                                                                            *\n *              See http://www.sympy.org/ for more information.               *\n *                                                                            *\n *                       This file is part of 'project'                       *\n ******************************************************************************/\n\n\n#ifndef PROJECT__OUTPUT__H\n#define PROJECT__OUTPUT__H\n\ndouble f(double x);\n\n#endif\n\n")]

Lambdify

La función lambdify() convierte expresiones simbólicas en funciones numéricas rápidas de Python. Por ejemplo, el código siguiente utiliza lambdify para convertir la expresión simbólica almacenada en el objeto f en una función Python rápida compatible con NumPy. Cuando se evalúa en el arreglo [1, 2, 3], devuelve [4, 9, 16]. 

from sympy import lambdify
import numpy as np

# Convert the symbolic expression into a fast numerical function using NumPy
f = lambdify(x, x**2 + 2*x + 1, 'numpy')

# Evaluate the function on a NumPy array
print(f(np.array([1, 2, 3])))

[ 4  9 16]

Consideraciones sobre el rendimiento

Dado que SymPy se centra en la precisión simbólica, puede ser más lento que los cálculos numéricos. Dicho esto, hay varias formas de mejorar el rendimiento cuando se trabaja con expresiones grandes o complicadas. 

Por ejemplo, puedes utilizar lambdify() para convertir expresiones simbólicas en funciones numéricas rápidas que funcionan bien con NumPy, o puedes simplificarlas antes de evaluarlas. 

Puedes acelerar aún más los cálculos pesados utilizando técnicas como la eliminación de subexpresiones comunes, la compilación automática de código y la integración con herramientas externas como Numba o Cython.

SymPy en el ecosistema Python

SymPy no funciona de forma aislada, sino que se integra perfectamente con otras herramientas populares utilizadas en ciencia de datos, educación e investigación, y encaja perfectamente en el ecosistema científico más amplio de Python.

Integración con otras bibliotecas

Puedes combinar SymPy con:

• NumPy/SciPy para cálculos numéricos de alto rendimiento
• Matplotlib para visualización
• Pandas para el análisis de datos simbólicos

import numpy as np
from sympy import lambdify

# Convert the symbolic expression x^2 into a fast NumPy-compatible function
f = lambdify(x, x**2, 'numpy')

# Evaluate the function on a NumPy array from 0 to 4
print(f(np.arange(5)))

[ 0  1  4  9 16]

Aplicaciones educativas

SymPy se utiliza ampliamente en las aulas y en entornos de autoaprendizaje porque refleja la forma en que se enseña las matemáticas en papel: paso a paso y de forma simbólica. En Jupyter Notebooks, los estudiantes pueden experimentar en directo con ecuaciones de álgebra, cálculo o física y ver resultados simbólicos exactosen lugar de aproximaciones aproximadas. Consulta la hoja de referencia rápida de Jupyter Notebook para empezar.

Proyectos e integraciones relacionados

SymPy también se conecta bien con otras potentes herramientas matemáticas, tales como:

• SageMath : un sistema matemático a gran escala que utiliza SymPy como backend.
• SymEngine : una reimplementación más rápida en C++ del núcleo de SymPy.
• Pyomo: integra modelos de optimización(consulta Optimización con Pyomo).

Comunidad, contribución y desarrollo

SymPy prospera gracias a una sólida comunidad de código abierto. Un grupo internacional de programadores, investigadores, profesores y estudiantes trabaja en SymPy, mejorándolo y haciéndolo más robusto día a día. Cualquiera puede ayudar, hacer preguntas o participar sin necesidad de permiso ni de ser miembro de la empresa.

Contribución y desarrollo

Las personas que desean ayudar suelen bifurcar el repositorio, realizar cambios, ejecutar el conjunto de pruebas con pytest y, a continuación, enviar una solicitud de extracción para su revisión.

Para garantizar que cada cambio sea fiable, se somete a un proceso de revisión del código. El proyecto también cuenta con un marco de pruebas para que los colaboradores puedan ejecutar pruebas en sus propios equipos antes de enviarlas. 

Informar de errores y solicitar asistencia

Para informar de errores o solicitar ayuda:

• Envía los problemas a GitHub en SymPy Issues.
• Pregunta en Stack Overflow 
• Únete a SymPy Gitter o a la lista de correo

Cuanto más claramente expliques el problema, incluyendo el código, lo que esperabas que sucediera, lo que realmente sucedió y qué versión de SymPy estás utilizando, más rápido podrá ayudarte la comunidad. 

Orientaciones futuras

SymPy sigue creciendo, y se sigue trabajando para ampliar sus funciones, mejorar su rendimiento e integrarlo con herramientas de inteligencia artificial. También se están realizando esfuerzos para mejorar la generación de código, la documentación y el uso educativo. Los nuevos colaboradores son especialmente bienvenidos para ayudar a clasificar los errores y problemas, mejorar la documentación y añadir nuevas funciones para las matemáticas simbólicas.

Conclusión

SymPy es una potente biblioteca que te permite utilizar matemáticas simbólicas en Python. Esto lo hace útil para la educación, la investigación e incluso el trabajo de ingeniería en el mundo real. Proporciona un ecosistema de código abierto, dentro del cual puedes realizar diversas operaciones y transformaciones matemáticas y algebraicas. SymPy es una herramienta que los estudiantes, programadores e investigadores deberían conocer. Así que adelante: abre un cuaderno Jupyter, importa sympy y empieza a explorar. 

También puedes consultar los siguientes recursos para obtener más información:

• Hoja de referencia de SciPy: Álgebra lineal en Python
• Documentación de SymPy
• Cómo elevar un número al cuadrado en Python