SymPy: Um guia completo para matemática simbólica em Python

Se você já quis que o Python fizesse e expressasse operações algébricas como um matemático, o SymPy é a resposta.

SymPy significa Symbolic Python (Python Simbólico) e é uma biblioteca criada para realizar cálculos simbólicos, o que significa que pode expandir, simplificar, diferenciar e resolver equações simbolicamente, tal como se faria em papel.  Uma extensão importante é que expressões matemáticas com variáveis não avaliadas são deixadas na forma simbólica. Por exemplo, a raiz quadrada de oito vai ser representada como 2*sqrt(2), em vez de aproximá-la para 2,828.   

Algumas das principais vantagens do SymPy são que ele é de código aberto, escrito totalmente em Python e oferece compatibilidade com outras bibliotecas Python. 

Principais vantagens do Sympy. Fonte: Imagem por Napkin AI

Breve história do SymPy

O SymPy começou com uma ideia simples: tornar a computação simbólica acessível a todos.

Foi criado em 2006 por Ondřej Čertík, um estudante da Universidade de Nevada. Ele queria criar uma biblioteca matemática simbólica leve e flexível em Python puro, para que as pessoas não precisassem lidar com as complexidades de grandes sistemas de álgebra computacional, como o Maple ou o Mathematica. 

Entre 2007 e 2010, o SymPy cresceu rapidamente ao participar do Google Summer of Code, durante o qual módulos centrais importantes, como simplificação, resolução e cálculo, foram significativamente expandidos. 

Por volta de 2012, o SymPy tinha amadurecido a ponto de ser integrado ao SageMath, mostrando que era reconhecido como um backend simbólico confiável dentro do ecossistema científico mais amplo do Python. Até hoje, o SymPy foi além do uso em álgebra e entrou em áreas mais avançadas, como física, geometria, combinatória, geração de código e ferramentas de compilação focadas em desempenho.

Começando com o SymPy

Antes de explorar a magia do SymPy, vamos configurá-lo corretamente.

Instalação e configuração

A maneira mais fácil de instalar o SymPy, que também é o método recomendado, é usando o pip:

pip install sympy

Se você estiver usando o Conda, o comando é:

conda install sympy

Ou então, você pode instalar direto da fonte (útil pra quem contribui):

git clone https://github.com/sympy/sympy.git

Se você está se perguntando sobre dependências: O SymPy funciona totalmente em Python e não depende de bibliotecas externas. Pacotes opcionais como mpmath podem ser instalados para aritmética de precisão arbitrária:

pip install mpmath

Verificando a instalação

Para confirmar a instalação, abra o Python e digite:

import sympy
print(sympy.__version__)

1.14.0

A saída mostra a versão instalada do pacote.  Agora você pode testar o pacote com uma expressão simples:

from sympy import symbols

# Define x as a symbolic variable
x = symbols('x')

print((x + 2)**2)

(x + 2)**2

Sobre a resolução de problemas:

• Se você vir “ ModuleNotFoundError ”, execute novamente “ pip install sympy ”.

• Se tiver conflitos de versão, atualize o pip: pip install --upgrade pip

Além disso, é bom saber que: Se você acha que tem algum bug ou quer pedir um recurso, pode abrirum ticket de problema. Para saber mais sobre como instalar, dá uma olhada na documentação oficial.

Uso básico

O SymPy oferece um ambiente interativo onde você pode mexer com expressões algébricas de forma simbólica.

from sympy import symbols, expand

#define x and y as symbolic variables
x, y = symbols('x y')

# create an algebraic expression
expr = (x + y)**2

expanded = expand(expr)
print(expanded)

x**2 + 2*x*y + y**2

A saída impressa acima x**2 + 2*x*y + y**2 é a forma totalmente expandida, mostrando como o SymPy faz álgebra simbólica exata em vez de cálculo numérico.

Principais recursos e funcionalidades

As principais funcionalidades são baseadas em cálculos simbólicos — ou seja, trabalhar com funções, equações e expressões como símbolos em vez de números.

Operações aritméticas

Você pode tratar variáveis simbólicas como variáveis algébricas. Além disso, as funções podem passar de um formulário para outro, como mostra o código abaixo. 

Usando expand() para distribuição e factor() para simplificação reversa, o SymPy transforma entre formas expandidas e fatoradas de uma expressão algébrica.

from sympy import symbols, expand, factor

# Define symbolic variables x and y
x, y = symbols('x y')

# Create an algebraic expression
expr = (x + y)**2

# Expand the expression to its full polynomial form
print(expand(expr))  

# Factor the expanded polynomial back into its compact form
print(factor(x**2 + 2*x*y + y**2)) 

x**2 + 2*x*y + y**2
(x + y)**2

Técnicas de simplificação

A simplificação é essencial para a computação simbólica. Tem uma função geral no Sympy, chamada ` simplify()`, que é usada pra simplificar expressões racionais, trigonométricas ou algébricas facilmente.

from sympy import simplify, trigsimp, sin, cos

# Create a trigonometric expression
expr = sin(x)**2 + cos(x)**2

# General simplification — recognizes that sin²x + cos²x = 1
print(simplify(expr)) 

# Trigonometric-specific simplification — also simplifies to 1
print(trigsimp(expr)) 

A saída nas funções simplify() e trigsimp() acima é um. 

Operações de cálculo

O SymPy é ótimo para cálculo porque permite fazer derivações, integrações, limites e até expansões em séries, tudo simbolicamente, como se fosse feito à mão, mas com precisão perfeita.

Diferenciação

Para calcular derivadas, use a função diff().

from sympy import diff

# Define a symbolic polynomial expression
f = x**3 + 2*x**2 + x

# Compute the derivative of the expression with respect to x
df = diff(f, x)
print(df)

3*x**2 + 4*x + 1

Integração

O código abaixo calcula a integral indefinida da expressão simbólica f em relação à variável x usando a função integrate() do SymPy. A antiderivada resultante é então impressa.

from sympy import integrate

# Compute the indefinite integral of the expression f with respect to x
integral = integrate(f, x)
print(integral)

x**4/4 + 2*x**3/3 + x**2/2

Limites

O cálculo do limite é uma operação clássica de cálculo, que pode ser feita usando a função limit() do SymPy. A sintaxe é: limit(f(x), x, x0).  Por exemplo, o código abaixo calcula o limite da expressão sin(x)/x quando x se aproxima de zero e mostra o resultado exato, one. 

from sympy import limit, sin

# Compute the limit of sin(x)/x as x approaches 0 
limit_expr = limit(sin(x)/x, x, 0)
print(limit_expr) 

Expansão em série

A função series() pode ser usada para calcular a expansão de Taylor ou série de potências de uma expressão matemática em torno de um ponto específico.

from sympy import series, exp

# Generate the Taylor series expansion of e^x around 0 up to 5 terms
print(series(exp(x), x, 0, 5))

1 + x + x**2/2 + x**3/6 + x**4/24 + O(x**5)

Resumos

A função summation() no SymPy faz uma soma simbólica exata em um certo intervalo, igual à notação sigma na matemática.

from sympy import summation, symbols

# Compute the symbolic sum of 1/n^2 from n = 1 to 5
n = symbols('n')
print(summation(1/n**2, (n, 1, 5)))  

5269/3600

Resolvendo equações

O SymPy facilita a resolução de equações simbólicas — não só as equações algébricas simples, mas também sistemas de equações, equações diferenciais e até equações diofantinas, que só têm números inteiros como soluções. 

Tem solucionadores poderosos como 

• solve() para equações algébricas, 

• linsolve() para sistemas lineares, e 

• dsolve() para equações diferenciais que dão soluções exatas sempre que possível. 

Equações algébricas

from sympy import Eq, solve
# Define and solve the equation x^2 - 4 = 0 symbolically
eq = Eq(x**2 - 4, 0)

print(solve(eq, x)) 

[-2, 2]

Sistemas de equações

from sympy import linsolve, symbols

# Solve a system of linear equations:
# x + y = 5  and  x - y = 1
x, y = symbols('x y')
sol = linsolve([x + y - 5, x - y - 1], (x, y))

print(sol) # Outputs the solution as a set (x, y)

{(3, 2)}

Equações diferenciais

from sympy import Function, dsolve

# Define y as a symbolic function of x
y = Function('y')

# Define a second-order differential equation
diff_eq = Eq(y(x).diff(x, 2) - y(x), 0)

# Solve the differential equation symbolically
print(dsolve(diff_eq))

Eq(y(x), C1*exp(-x) + C2*exp(x))

Operações matriciais

O SymPy é uma ótima ferramenta para álgebra linear, pois suporta matrizes simbólicas. Você pode facilmente trabalhar com matrizes e fazer operações matemáticas como adição e multiplicação, assim como faria na álgebra normal. 

from sympy import Matrix

# Define symbolic matrices A and B
A = Matrix([[1, 2], [x, 3]])
B = Matrix([[x], [4]])

# Perform matrix multiplication
print(A * B)

Matrix([[x + 8], [x**2 + 12]])

Operações avançadas

O SymPy também permite calcular propriedades importantes de matrizes, como determinantes, inversas, autovalores e autovetores simbolicamente, fornecendo respostas exatas. 

# Compute the determinant of matrix A
A.det()      

# Compute the inverse of matrix A
A.inv()      

# Compute the eigenvalues of matrix A
A.eigenvals() 

{2 - sqrt(2*x + 1): 1, sqrt(2*x + 1) + 2: 1}

Recursos de plotagem

O SymPy não se limita à computação simbólica — ele também suporta a visualização de expressões matemáticas. Usando os utilitários de plotagem integrados, você pode gerar gráficos 2D e até 3D de funções simbólicas com poucas linhas de código. 

Por exemplo, o código abaixo gera um gráfico 2D:  

from sympy.plotting import plot


# Plot the function x^2 over the range -5 to 5
plot(x**2, (x, -5, 5))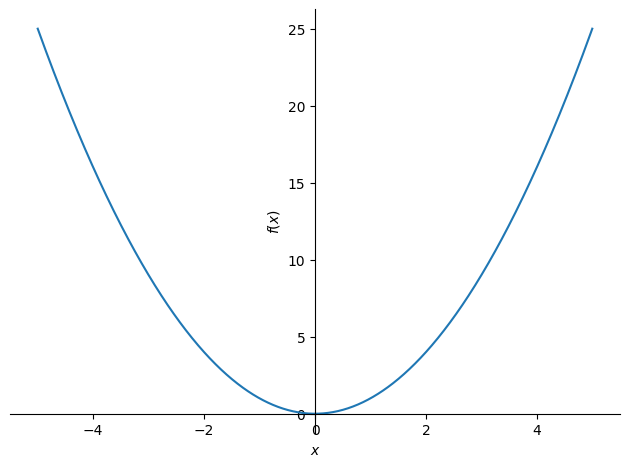

Gráfico 2D feito com o SymPy. 

Para gerar gráficos 3D, você pode usar a função ` plot3d() `, como mostrado abaixo.

from sympy.plotting import plot3d
from sympy import sin

# Generate a 3D surface plot of the function sin(x*y) over the specified x and y ranges
plot3d(sin(x*y), (x, -5, 5), (y, -5, 5))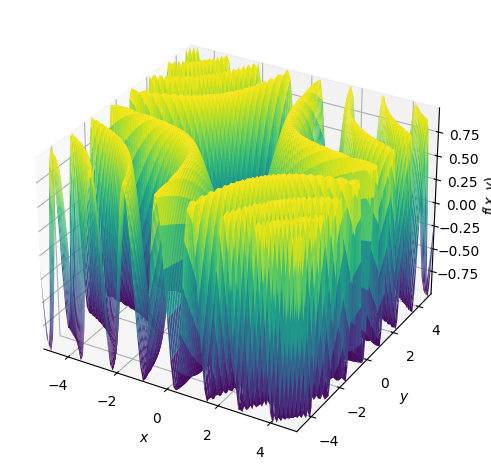

Capacidade de plotagem 3D do SymPy

E se você precisar de mais controle ou estilo, o SymPy também pode se integrar com o Matplotlib para permitir visualizações totalmente personalizáveis. Para visualizações mais avançadas, dá uma olhada no nosso tutorial sobre Plotly Shapes.

Recursos avançados

O SymPy vai muito além da álgebra básica — ele se estende a polinômios, combinatória e até mesmo física.

Manipulação polinomial

Você pode definir e mexer com polinômios facilmente. O código abaixo cria um objeto polinomial a partir da expressão; e, em seguida, imprime seu grau, forma fatorada com coeficientes usando a função Poly() do SymPy. 

from sympy import Poly

# Create a symbolic polynomial in variable x
p = Poly(x**3 - 3*x**2 + x - 3, x)

# Print the degree of the polynomial (highest power of x)
print(p.degree())  

# Print the factorized form of the polynomial along with coefficients
print(p.factor_list())  

3
(1, [(Poly(x - 3, x, domain='ZZ'), 1), (Poly(x**2 + 1, x, domain='ZZ'), 1)])

Para sistemas polinomiais complexos, as bases de Gröbner são suportadas, que são uma versão simplificada e padronizada de um sistema de equações polinomiais, tornando-as mais fáceis de resolver. 

Por exemplo, o código abaixo calcula a base de Gröbner para o sistema polinomial [x*y - 1, y - x], o que significa que ele reescreve as equações em uma forma mais simples e estruturada, mais fácil de resolver. A saída mostra que o sistema é igual às equações mais simples x = y e y² = 1, que agora podem ser resolvidas direto.

from sympy import groebner, symbols

# Define x and y as symbolic variables
x, y = symbols('x y')

# Compute the Gröbner basis for the system of polynomial equations
print(groebner([x*y - 1, y - x], x, y))

GroebnerBasis([x - y, y**2 - 1], x, y, domain='ZZ', order='lex')

Combinatória, matemática discreta e teoria dos números

O SymPy tem vários utilitários que permitem lidar com problemas combinatórios e de teoria dos números. 

Por exemplo, no código abaixo:

• A função binomial(5, 2) calcula quantas maneiras existem de escolher 2 itens entre 5 (um problema de combinação). 

• factorial(6) calcula 6!, uma operação comum em permutações. 

• isprime(19) verifica se 19 é um número primo e 

• factorint(100) retorna sua fatoração primária exata como um {2: 2, 5: 2}. 

from sympy import binomial, factorial, isprime, factorint
print(binomial(5, 2))   # 10
print(factorial(6))     # 720
print(isprime(19))      # True
print(factorint(100))   # {2: 2, 5: 2}

10
720
True
{2: 2, 5: 2}

10
720
True
{2: 2, 5: 2}

Juntas, essas funções mostram como o SymPy lida com matemática discreta com facilidade e precisão. Você também pode trabalhar diretamente com partições, permutações e combinações.

Aplicações em geometria e física

O SymPy não é só pra álgebra e cálculo; ele também tem módulos especiais pra geometria e física. 

No módulo de geometria, você pode definir objetos matemáticos como pontos, linhas, círculos e polígonos. Usando símbolos, você também pode obter equações de retas, interseções, distâncias e pontos médios. 

Por exemplo, pra fazer dois pontos e desenhar uma linha entre eles, é só fazer assim:

from sympy import Point, Line, Circle

# Define two points and create a line passing through them
A, B = Point(0, 0), Point(1, 1)
L = Line(A, B)

# Print the symbolic equation of the line
print(L.equation())  

-x + y

Além dos recursos de geometria, o SymPy tem um módulo de física super útil. Com esse módulo, você pode modelar mecânica clássica, sistemas quânticos, unidades e tamanhos.  Isso vale tanto se você estiver usando metros por segundo para calcular a velocidade quanto resolvendo equações de movimento com símbolos. 

from sympy.physics.units import meter, second

# Define a symbolic physical quantity: velocity = 10 meters per second
velocity = 10 * meter / second
print(velocity)

10*meter/second

Impressão e saída LaTeX

O SymPy permite imprimir expressões simbólicas em vários formatos, incluindo:

• Impressão bonita e fácil de ler 
• Saída baseada em Unicode e 
• LaTeX, que é a linguagem de formatação padrão usada em artigos de pesquisa e documentos científicos. 

Você pode usar funções como pprint() para deixar suas equações com uma aparência elegante e profissional em um notebook Jupyter ou ao produzir um relatório. Você pode até usar latex() para prepará-los para um trabalho de pesquisa. Isso evita o trabalho de ter que formatar tudo você mesmo.

from sympy import pprint, latex, symbols

# Define x and y as symbolic variables
x, y = symbols('x y')

# Now you can perform symbolic math operations
expr = (x+y)**3

# Pretty print to the console
pprint(expr)

# Print the LaTeX string
print(latex(expr))

     3
(x + y) 
\left(x + y\right)^{3}

Geração de código e otimização de desempenho

Embora o SymPy seja ótimo em cálculos simbólicos, ele também permite converter expressões simbólicas em código executável otimizado para uso numérico de alto desempenho.

O código abaixo usa a utilidade codegen() do SymPy para gerar automaticamente código em linguagem C a partir de uma expressão simbólica, deixando-o pronto para uso em aplicações incorporadas.

from sympy.utilities.codegen import codegen

# Generate C code for the symbolic function and save it as 'output'
codegen(("f", x**2 + 1), "C", "output")

[('output.c',
  '/******************************************************************************\n *                      Code generated with SymPy 1.14.0                      *\n *                                                                            *\n *              See http://www.sympy.org/ for more information.               *\n *                                                                            *\n *                       This file is part of \'project\'                       *\n ******************************************************************************/\n#include "output.h"\n#include <math.h>\n\ndouble f(double x) {\n\n   double f_result;\n   f_result = pow(x, 2) + 1;\n   return f_result;\n\n}\n'),
 ('output.h',
  "/******************************************************************************\n *                      Code generated with SymPy 1.14.0                      *\n *                                                                            *\n *              See http://www.sympy.org/ for more information.               *\n *                                                                            *\n *                       This file is part of 'project'                       *\n ******************************************************************************/\n\n\n#ifndef PROJECT__OUTPUT__H\n#define PROJECT__OUTPUT__H\n\ndouble f(double x);\n\n#endif\n\n")]

Lambdify

A função ` lambdify() ` transforma expressões simbólicas em funções numéricas rápidas do Python. Por exemplo, o código abaixo usa lambdify para converter a expressão simbólica armazenada sob o objeto, f, em uma função Python rápida compatível com NumPy. Quando avaliado na matriz [1, 2, 3], ele retorna [4, 9, 16]. 

from sympy import lambdify
import numpy as np

# Convert the symbolic expression into a fast numerical function using NumPy
f = lambdify(x, x**2 + 2*x + 1, 'numpy')

# Evaluate the function on a NumPy array
print(f(np.array([1, 2, 3])))

[ 4  9 16]

Considerações sobre desempenho

Como o SymPy se preocupa com a precisão simbólica, ele pode ser mais lento do que os cálculos numéricos. Dito isso, tem várias maneiras de melhorar o desempenho ao trabalhar com expressões grandes ou complicadas. 

Por exemplo, você pode usar lambdify() para transformar expressões simbólicas em funções numéricas rápidas que funcionam bem com o NumPy, ou pode simplificá-las antes de avaliá-las. 

Você pode acelerar ainda mais cálculos pesados usando técnicas como eliminação de subexpressões comuns, compilação automática de código e integração com ferramentas externas como Numba ou Cython.

SymPy no ecossistema Python

O SymPy não funciona sozinho — ele se integra bem com outras ferramentas populares usadas em ciência de dados, educação e pesquisa e se encaixa perfeitamente no grande ecossistema científico do Python.

Integração com outras bibliotecas

Você pode juntar o SymPy com:

• NumPy/SciPy para cálculos numéricos de alto desempenho
• Matplotlib para visualização
• Pandas para análise de dados simbólicos

import numpy as np
from sympy import lambdify

# Convert the symbolic expression x^2 into a fast NumPy-compatible function
f = lambdify(x, x**2, 'numpy')

# Evaluate the function on a NumPy array from 0 to 4
print(f(np.arange(5)))

[ 0  1  4  9 16]

Aplicações educacionais

O SymPy é muito usado em salas de aula e ambientes de autoaprendizagem porque reflete a forma como a matemática é ensinada no papel — passo a passo e simbolicamente. Nos Jupyter Notebooks, os alunos podem experimentar ao vivo equações de álgebra, cálculo ou física e ver resultados simbólicos exatos em vez de aproximações aproximadas. Dá uma olhada na Folha de Referência do Jupyter Notebook pra começar.

Projetos e integrações relacionados

O SymPy também se conecta bem com outras ferramentas matemáticas poderosas, como:

• SageMath — um sistema matemático de grande escala que usa o SymPy como backend.
• SymEngine — uma reimplementação mais rápida em C++ do núcleo do SymPy.
• Pyomo — junta modelagem de otimização(veja Otimizando com Pyomo).

Comunidade, Contribuição e Desenvolvimento

O SymPy prospera graças a uma forte comunidade de código aberto. Um grupo mundial de desenvolvedores, pesquisadores, professores e estudantes trabalha no SymPy, tornando-o melhor e mais robusto a cada dia. Qualquer pessoa pode ajudar, fazer perguntas ou participar sem precisar de permissão ou ser membro corporativo.

Contribuição e desenvolvimento

Quem quiser ajudar geralmente faz um fork do repositório, faz as alterações, roda o conjunto de testes com o comando ` pytest` e, em seguida, envia uma solicitação pull para revisão.

Para garantir que todas as alterações sejam confiáveis, elas passam por um processo de revisão de código. O projeto também tem uma estrutura de testes para que os colaboradores possam fazer testes em seus próprios computadores antes de enviar. 

Relatando bugs e pedindo ajuda

Para bugs ou ajuda:

• Registre os problemas no GitHub em SymPy Issues.
• Pergunte no Stack Overflow 
• Junte-se ao SymPy Gitter ou à lista de discussão

Quanto mais claramente você explicar o problema, incluindo o código, o que você esperava que acontecesse, o que realmente aconteceu e qual versão do SymPy você está usando, mais rápido a comunidade poderá ajudar. 

Direções futuras

O SymPy continua crescendo, com trabalhos em andamento para expandir seus recursos, melhorar seu desempenho e integrá-lo a ferramentas de IA. Também tem gente tentando melhorar a geração de código, a documentação e o uso educacional. Novos colaboradores são super bem-vindos pra ajudar a resolver os bugs e problemas, melhorar a documentação e adicionar novos recursos pra matemática simbólica.

Conclusão

SymPy é uma biblioteca poderosa que permite usar matemática simbólica em Python. Isso torna-o útil para educação, pesquisa e até mesmo trabalhos de engenharia no mundo real. Ele oferece um ecossistema de código aberto, onde você pode fazer várias operações e transformações matemáticas e algébricas. O SymPy é uma ferramenta que estudantes, desenvolvedores e pesquisadores deveriam dar uma olhada. Então vá em frente — abra um notebook Jupyter, importe sympy e comece a explorar. 

Você também pode conferir os seguintes recursos para ler mais sobre o assunto:

• Folha de dicas do SciPy: Álgebra Linear em Python
• Documentação do SymPy
• Como elevar um número ao quadrado em Python