SymPy: Ein kompletter Leitfaden zur symbolischen Mathematik in Python

Wenn du schon immer mal Python dazu bringen wolltest, algebraische Operationen wie ein Mathegenie zu machen und auszudrücken, dann ist SymPy genau das Richtige für dich.

SymPy steht für Symbolic Python und ist eine Bibliothek, die für symbolische Berechnungen entwickelt wurde. Das heißt, sie kann Gleichungen symbolisch erweitern, vereinfachen, differenzieren und lösen, genau wie man es auf Papier machen würde.  Eine wichtige Erweiterung ist, dass mathematische Ausdrücke mit nicht ausgewerteten Variablen in symbolischer Form bleiben ( ). Zum Beispiel wird die Quadratwurzel von acht als „ 2*sqrt(2) “ dargestellt, statt sie auf 2,828 zu runden.   

Ein paar der größten Vorteile von SymPy sind, dass es Open Source ist, komplett in Python geschrieben wurde und mit anderen Python-Bibliotheken kompatibel ist. 

Die wichtigsten Vorteile von Sympy. Quelle: Bild von Napkin AI

Kurze Geschichte von SymPy

SymPy fing mit einer einfachen Idee an: symbolische Berechnungen für alle zugänglich zu machen.

Es wurde 2006 von Ondřej Čertík, einem Studenten der Universität von Nevada, ins Leben gerufen. Er wollte eine leichte, flexible Bibliothek für symbolische Mathematik in reinem Python erstellen, damit man sich nicht mit den Komplexitäten großer Computeralgebrasysteme wie Maple oder Mathematica herumschlagen muss. 

Zwischen 2007 und 2010 hat sich SymPy schnell weiterentwickelt, weil es beim Google Summer of Code mitgemacht hat. In dieser Zeit wurden wichtige Kernmodule wie Vereinfachung, Lösung und Kalkül stark ausgebaut. 

Um 2012 war SymPy so weit entwickelt, dass es in SageMath eingebaut wurde, was zeigt, dass es als zuverlässiges symbolisches Backend im größeren wissenschaftlichen Python-Umfeld anerkannt wurde. Mittlerweile ist SymPy nicht mehr nur für Algebra da, sondern hat sich zu einem Tool für anspruchsvolle Bereiche wie Physik, Geometrie, Kombinatorik, Codegenerierung und leistungsorientierte Kompilierungswerkzeuge entwickelt.

SymPy für Anfänger

Bevor wir uns mit den coolen Funktionen von SymPy beschäftigen, lass uns das Programm erst mal richtig einrichten.

Installation und Einrichtung

Der einfachste Weg, SymPy zu installieren, und auch die empfohlene Methode, ist mit pip:

pip install sympy

Wenn du Conda benutzt, lautet der Befehl:

conda install sympy

Du kannst es auch direkt aus dem Quellcode installieren (praktisch für Mitwirkende):

git clone https://github.com/sympy/sympy.git

Wenn du dich über Abhängigkeiten wunderst: SymPy läuft komplett in Python und braucht keine externen Bibliotheken. Optionale Pakete wie „ mpmath “ können für Arithmetik mit beliebiger Genauigkeit installiert werden:

pip install mpmath

Installation überprüfen

Um die Installation zu checken, öffne Python und gib Folgendes ein:

import sympy
print(sympy.__version__)

1.14.0

Die Ausgabe zeigt die installierte Version des Pakets.  Du kannst das Paket jetzt mit einem einfachen Ausdruck testen:

from sympy import symbols

# Define x as a symbolic variable
x = symbols('x')

print((x + 2)**2)

(x + 2)**2

Was die Fehlerbehebung angeht:

• Wenn du die Meldung „ ModuleNotFoundError “ siehst, starte „ pip install sympy “ einfach nochmal.

• Bei Versionskonflikten pip aktualisieren: pip install --upgrade pip

Außerdem ist es gut zu wissen: IchWenn du denkst, dass es einen Fehler gibt, oder eine Funktion haben möchtest, kannst du auchein Ticketerstellen. Schau dir die offizielle Dokumentation an, wenn du mehr über die Installationsmethoden erfahren willst.

Einfache Nutzung

SymPy bietet eine interaktive Umgebung, in der du algebraische Ausdrücke symbolisch bearbeiten kannst.

from sympy import symbols, expand

#define x and y as symbolic variables
x, y = symbols('x y')

# create an algebraic expression
expr = (x + y)**2

expanded = expand(expr)
print(expanded)

x**2 + 2*x*y + y**2

Die gedruckte Ausgabe über „ x**2 + 2*x*y + y**2 “ ist die vollständig erweiterte Form, die zeigt, wie SymPy exakte symbolische Algebra statt numerischer Berechnung durchführt.

Wichtigste Features und Funktionen

Die Hauptfunktionen drehen sich um symbolische Berechnungen – das heißt, man arbeitet mit Funktionen, Gleichungen und Ausdrücken als Symbole statt mit Zahlen.

Rechenoperationen

Du kannst symbolische Variablen wie algebraische behandeln. Außerdem können die Funktionen von einem Formular zum anderen verschoben werden, wie im folgenden Code gezeigt wird. 

Mit der Verwendung von „ expand() “ für die Verteilung und „ factor() “ für die umgekehrte Vereinfachung wandelt SymPy zwischen erweiterten und faktorisierten Formen eines algebraischen Ausdrucks um.

from sympy import symbols, expand, factor

# Define symbolic variables x and y
x, y = symbols('x y')

# Create an algebraic expression
expr = (x + y)**2

# Expand the expression to its full polynomial form
print(expand(expr))  

# Factor the expanded polynomial back into its compact form
print(factor(x**2 + 2*x*y + y**2)) 

x**2 + 2*x*y + y**2
(x + y)**2

Techniken zur Vereinfachung

Vereinfachung ist echt wichtig bei symbolischen Berechnungen. Sympy hat eine allgemeine Funktion namens „ simplify() “, mit der man rationale, trigonometrische oder algebraische Ausdrücke ganz einfach vereinfachen kann.

from sympy import simplify, trigsimp, sin, cos

# Create a trigonometric expression
expr = sin(x)**2 + cos(x)**2

# General simplification — recognizes that sin²x + cos²x = 1
print(simplify(expr)) 

# Trigonometric-specific simplification — also simplifies to 1
print(trigsimp(expr)) 

Die Ausgabe der beiden oben genannten Funktionen „ simplify() “ und „ trigsimp() “ ist eins. 

Differentialrechnung

SymPy ist super für die Analysis, weil du damit Ableitungen, Integrationen, Grenzwerte und sogar Reihenentwicklungen ganz symbolisch machen kannst, genau wie beim Rechnen mit der Hand, aber mit perfekter Genauigkeit.

Differenzierung

Um Ableitungen zu bilden, benutze die Funktion „ diff() “.

from sympy import diff

# Define a symbolic polynomial expression
f = x**3 + 2*x**2 + x

# Compute the derivative of the expression with respect to x
df = diff(f, x)
print(df)

3*x**2 + 4*x + 1

Integration

Der Code unten berechnet die unbestimmte Integral des symbolischen Ausdrucks f in Bezug auf die Variable x mit der SymPy-Funktion integrate(). Die resultierende Stammfunktion wird dann ausgegeben.

from sympy import integrate

# Compute the indefinite integral of the expression f with respect to x
integral = integrate(f, x)
print(integral)

x**4/4 + 2*x**3/3 + x**2/2

Grenzen

Die Berechnung der Grenze ist eine klassische Rechenoperation, die mit der SymPy-Funktion „ limit() “ gemacht werden kann. Die Syntax ist: limit(f(x), x, x0).  Der Code unten berechnet zum Beispiel den Grenzwert des Ausdrucks „ sin(x)/x “, wenn „ x “ gegen Null geht, und zeigt das genaue Ergebnis „ one “ an. 

from sympy import limit, sin

# Compute the limit of sin(x)/x as x approaches 0 
limit_expr = limit(sin(x)/x, x, 0)
print(limit_expr) 

Reihenentwicklung

Mit der Funktion „ series() “ kannst du die Taylor- oder Potenzreihenentwicklung eines mathematischen Ausdrucks um einen bestimmten Punkt herum berechnen.

from sympy import series, exp

# Generate the Taylor series expansion of e^x around 0 up to 5 terms
print(series(exp(x), x, 0, 5))

1 + x + x**2/2 + x**3/6 + x**4/24 + O(x**5)

Zusammenfassungen

Die Funktion „ summation() ” in SymPy macht eine exakte symbolische Summierung über einen bestimmten Bereich, genau wie die Sigma-Notation in der Mathe.

from sympy import summation, symbols

# Compute the symbolic sum of 1/n^2 from n = 1 to 5
n = symbols('n')
print(summation(1/n**2, (n, 1, 5)))  

5269/3600

Lösen von Gleichungen

SymPy macht es einfach, symbolische Gleichungen zu lösen – nicht nur die einfachen algebraischen, sondern auch Gleichungssysteme, Differentialgleichungen und sogar diophantische Gleichungen, die nur ganze Zahlen als Lösungen haben. 

Es hat echt starke Solver wie 

• solve() für algebraische Gleichungen, 

• linsolve() für lineare Systeme und 

• dsolve() für Differentialgleichungen, die, wenn möglich, exakte Lösungen liefern. 

Algebraische Gleichungen

from sympy import Eq, solve
# Define and solve the equation x^2 - 4 = 0 symbolically
eq = Eq(x**2 - 4, 0)

print(solve(eq, x)) 

[-2, 2]

Gleichungssysteme

from sympy import linsolve, symbols

# Solve a system of linear equations:
# x + y = 5  and  x - y = 1
x, y = symbols('x y')
sol = linsolve([x + y - 5, x - y - 1], (x, y))

print(sol) # Outputs the solution as a set (x, y)

{(3, 2)}

Differentialgleichungen

from sympy import Function, dsolve

# Define y as a symbolic function of x
y = Function('y')

# Define a second-order differential equation
diff_eq = Eq(y(x).diff(x, 2) - y(x), 0)

# Solve the differential equation symbolically
print(dsolve(diff_eq))

Eq(y(x), C1*exp(-x) + C2*exp(x))

Matrixoperationen

SymPy ist echt super für lineare Algebra, weil es symbolische Matrizen unterstützt. Du kannst ganz einfach mit Matrizen arbeiten und mathematische Operationen wie Addition und Multiplikation durchführen, genau wie in der normalen Algebra. 

from sympy import Matrix

# Define symbolic matrices A and B
A = Matrix([[1, 2], [x, 3]])
B = Matrix([[x], [4]])

# Perform matrix multiplication
print(A * B)

Matrix([[x + 8], [x**2 + 12]])

Erweiterte Funktionen

Mit SymPy kannst du auch wichtige Matrixeigenschaften wie Determinanten, Inverse, Eigenwerte und Eigenvektoren symbolisch berechnen und bekommst so genaue Antworten. 

# Compute the determinant of matrix A
A.det()      

# Compute the inverse of matrix A
A.inv()      

# Compute the eigenvalues of matrix A
A.eigenvals() 

{2 - sqrt(2*x + 1): 1, sqrt(2*x + 1) + 2: 1}

Plotterfunktionen

SymPy kann nicht nur symbolische Berechnungen machen, sondern zeigt auch mathematische Ausdrücke an. Mit den eingebauten Plotting-Tools kannst du mit nur wenigen Zeilen Code 2D- und sogar 3D-Plots von symbolischen Funktionen erstellen. 

Der folgende Code macht zum Beispiel ein 2D-Diagramm:  

from sympy.plotting import plot


# Plot the function x^2 over the range -5 to 5
plot(x**2, (x, -5, 5))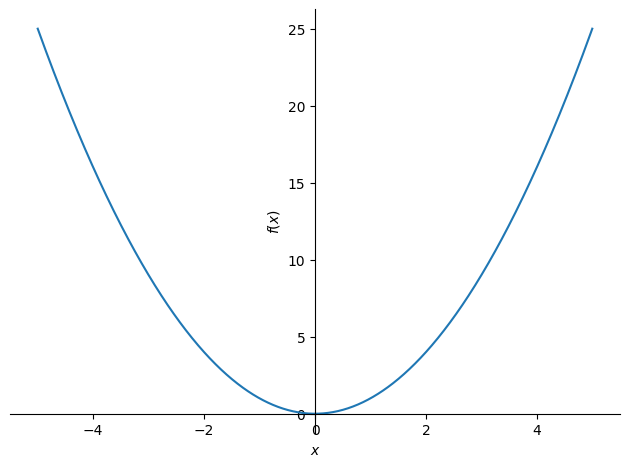

Mit SymPy erstellte 2D-Grafik. 

Um 3D-Plots zu erstellen, kannst du die Funktion „ plot3d() “ wie unten gezeigt verwenden.

from sympy.plotting import plot3d
from sympy import sin

# Generate a 3D surface plot of the function sin(x*y) over the specified x and y ranges
plot3d(sin(x*y), (x, -5, 5), (y, -5, 5))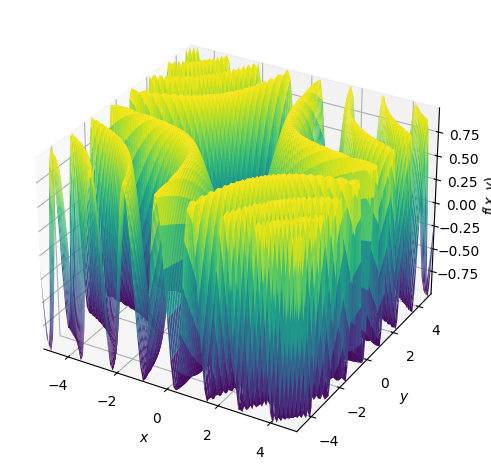

3D-Plotting-Fähigkeit von SymPy

Und wenn du mehr Kontrolle oder Styling brauchst, kann SymPy auch mit Matplotlib integriert werden, um komplett anpassbare Visualisierungen zu ermöglichen. Für fortgeschrittenere Visualisierungen schau dir unser Tutorial zu Plotly Shapes.

Erweiterte Funktionen

SymPy geht weit über die einfache Algebra hinaus – es geht auch um Polynome, Kombinatorik und sogar Physik.

Manipulation von Polynomen

Du kannst Polynome ganz einfach definieren und bearbeiten. Der Code unten macht aus dem Ausdruck ein Polynomobjekt und zeigt dann seinen Grad und die faktorisierte Form mit Koeffizienten an, indem er die SymPy-Funktion „ Poly() “ benutzt. 

from sympy import Poly

# Create a symbolic polynomial in variable x
p = Poly(x**3 - 3*x**2 + x - 3, x)

# Print the degree of the polynomial (highest power of x)
print(p.degree())  

# Print the factorized form of the polynomial along with coefficients
print(p.factor_list())  

3
(1, [(Poly(x - 3, x, domain='ZZ'), 1), (Poly(x**2 + 1, x, domain='ZZ'), 1)])

Für komplizierte Polynomsysteme gibt's Gröbner-Basen, die sind so 'ne vereinfachte und standardisierte Version von Polynomgleichungssystemen, damit sie einfacher zu lösen sind. 

Der Code unten berechnet zum Beispiel die Gröbner-Basis für das Polynomsystem „ [x*y - 1, y - x] “. Das heißt, er schreibt die Gleichungen in eine einfachere, strukturiertere Form um, die leichter zu lösen ist. Die Ausgabe zeigt, dass das System den saubereren Gleichungen x = y und y² = 1 entspricht, die jetzt direkt gelöst werden können.

from sympy import groebner, symbols

# Define x and y as symbolic variables
x, y = symbols('x y')

# Compute the Gröbner basis for the system of polynomial equations
print(groebner([x*y - 1, y - x], x, y))

GroebnerBasis([x - y, y**2 - 1], x, y, domain='ZZ', order='lex')

Kombinatorik, diskrete Mathematik und Zahlentheorie

SymPy hat ein paar Tools, mit denen man kombinatorische und zahlentheoretische Probleme lösen kann. 

Zum Beispiel im folgenden Code:

• Die Funktion „ binomial(5, 2) “ zählt, wie viele Möglichkeiten es gibt, 2 Elemente aus 5 auszuwählen (ein Kombinationsproblem). 

• factorial(6) berechnet 6!, eine gängige Operation bei Permutationen. 

• isprime(19) prüft, ob 19 eine Primzahl ist, und 

• factorint(100) gibt die genaue Primfaktorzerlegung als „ {2: 2, 5: 2} “ zurück. 

from sympy import binomial, factorial, isprime, factorint
print(binomial(5, 2))   # 10
print(factorial(6))     # 720
print(isprime(19))      # True
print(factorint(100))   # {2: 2, 5: 2}

10
720
True
{2: 2, 5: 2}

10
720
True
{2: 2, 5: 2}

Zusammen zeigen diese Funktionen, wie SymPy diskrete Mathematik einfach und genau handhabt. Du kannst auch direkt mit Partitionen, Permutationen und Kombinationen arbeiten.

Anwendungen in Geometrie und Physik

SymPy ist nicht nur für Algebra und Analysis gedacht, sondern hat auch spezielle Module für Geometrie und Physik. 

Im Geometriemodul kannst du mathematische Objekte wie Punkte, Linien, Kreise und Polygone festlegen. Mit Symbolen kannst du auch Gleichungen für Geraden, Schnittpunkte, Abstände und Mittelpunkte finden. 

Um zum Beispiel zwei Punkte zu setzen und eine Linie zwischen ihnen zu zeichnen, machst du einfach Folgendes:

from sympy import Point, Line, Circle

# Define two points and create a line passing through them
A, B = Point(0, 0), Point(1, 1)
L = Line(A, B)

# Print the symbolic equation of the line
print(L.equation())  

-x + y

Neben den Geometriefunktionen hat SymPy auch ein echt nützliches Physikmodul. Mit diesem Modul kannst du klassische Mechanik, Quantensysteme, Einheiten und Größen modellieren.  Das gilt egal, ob du Meter pro Sekunde benutzt, um die Geschwindigkeit zu berechnen, oder Bewegungsgleichungen mit Symbolen löst. 

from sympy.physics.units import meter, second

# Define a symbolic physical quantity: velocity = 10 meters per second
velocity = 10 * meter / second
print(velocity)

10*meter/second

Drucken und LaTeX-Ausgabe

Mit SymPy kannst du symbolische Ausdrücke in verschiedenen Formaten ausdrucken, zum Beispiel:

• Menschenfreundliches Pretty Printing 
• Unicode-basierte Ausgabe und 
• LaTeX, die Standard-Formatierungssprache für Forschungsarbeiten und wissenschaftliche Dokumente. 

Du kannst Funktionen wie „ pprint() “ nutzen, um deine Gleichungen in einem Jupyter-Notebook oder beim Erstellen eines Berichts ordentlich und professionell aussehen zu lassen. Du kannst sogar „ latex() “ nutzen, um sie für eine Forschungsarbeit vorzubereiten. Du sparst dir die Mühe, alles selbst formatieren zu müssen.

from sympy import pprint, latex, symbols

# Define x and y as symbolic variables
x, y = symbols('x y')

# Now you can perform symbolic math operations
expr = (x+y)**3

# Pretty print to the console
pprint(expr)

# Print the LaTeX string
print(latex(expr))

     3
(x + y) 
\left(x + y\right)^{3}

Codegenerierung und Leistungsoptimierung

SymPy ist super bei symbolischen Berechnungen, aber du kannst damit auch symbolische Ausdrücke in optimierten ausführbaren Code für leistungsstarke numerische Anwendungen umwandeln.

Der Code unten nutzt das SymPy-Tool „ codegen() “, um automatisch C-Code aus einem symbolischen Ausdruck zu machen, sodass er in eingebetteten Anwendungen verwendet werden kann.

from sympy.utilities.codegen import codegen

# Generate C code for the symbolic function and save it as 'output'
codegen(("f", x**2 + 1), "C", "output")

[('output.c',
  '/******************************************************************************\n *                      Code generated with SymPy 1.14.0                      *\n *                                                                            *\n *              See http://www.sympy.org/ for more information.               *\n *                                                                            *\n *                       This file is part of \'project\'                       *\n ******************************************************************************/\n#include "output.h"\n#include <math.h>\n\ndouble f(double x) {\n\n   double f_result;\n   f_result = pow(x, 2) + 1;\n   return f_result;\n\n}\n'),
 ('output.h',
  "/******************************************************************************\n *                      Code generated with SymPy 1.14.0                      *\n *                                                                            *\n *              See http://www.sympy.org/ for more information.               *\n *                                                                            *\n *                       This file is part of 'project'                       *\n ******************************************************************************/\n\n\n#ifndef PROJECT__OUTPUT__H\n#define PROJECT__OUTPUT__H\n\ndouble f(double x);\n\n#endif\n\n")]

Lambdify

Die Funktion „ lambdify() ” macht aus symbolischen Ausdrücken schnelle numerische Python-Funktionen. Der Code unten nutzt zum Beispiel „ lambdify “, um den symbolischen Ausdruck, der unter dem Objekt „ f “ gespeichert ist, in eine schnelle NumPy-kompatible Python-Funktion umzuwandeln. Wenn man das Array [1, 2, 3] damit durchrechnet, kriegt man [4, 9, 16]. 

from sympy import lambdify
import numpy as np

# Convert the symbolic expression into a fast numerical function using NumPy
f = lambdify(x, x**2 + 2*x + 1, 'numpy')

# Evaluate the function on a NumPy array
print(f(np.array([1, 2, 3])))

[ 4  9 16]

Leistungsaspekte

Weil SymPy auf symbolische Genauigkeit ausgerichtet ist, kann es langsamer sein als numerische Berechnungen. Trotzdem gibt es ein paar Möglichkeiten, die Leistung bei der Arbeit mit großen oder komplizierten Ausdrücken zu verbessern. 

Du kannst zum Beispiel „ lambdify() “ nutzen, um symbolische Ausdrücke in schnelle numerische Funktionen umzuwandeln, die gut mit NumPy funktionieren, oder du kannst sie vor der Auswertung vereinfachen. 

Du kannst rechenintensive Vorgänge noch weiter beschleunigen, indem du Techniken wie die Eliminierung gemeinsamer Unterausdrücke, die automatische Code-Kompilierung und die Integration mit externen Tools wie Numba oder Cython einsetzt.

SymPy im Python-Ökosystem

SymPy arbeitet nicht isoliert – es lässt sich gut mit anderen beliebten Tools aus den Bereichen Datenwissenschaft, Bildung und Forschung kombinieren und fügt sich nahtlos in das größere wissenschaftliche Python-Ökosystem ein.

Integration mit anderen Bibliotheken

Du kannst SymPy mit folgenden Programmen kombinieren:

• NumPy/SciPy für super schnelle Berechnungen
• Matplotlib für die Visualisierung
• Pandas für symbolische Datenanalyse

import numpy as np
from sympy import lambdify

# Convert the symbolic expression x^2 into a fast NumPy-compatible function
f = lambdify(x, x**2, 'numpy')

# Evaluate the function on a NumPy array from 0 to 4
print(f(np.arange(5)))

[ 0  1  4  9 16]

Bildungsanwendungen

SymPy wird oft im Unterricht und beim Selbststudium benutzt, weil es so funktioniert, wie man Mathe normalerweise auf Papier lernt – Schritt für Schritt und mit Symbolen. In Jupyter Notebooks können Schüler live mit Algebra-, Integralrechnung- oder Physikgleichungen experimentieren und genaue symbolische Ergebnisse sehen, statt nur grobe Schätzungen. Schau dir das Jupyter Notebook Cheat Sheet an, um loszulegen.

Ähnliche Projekte und Integrationen

SymPy lässt sich auch super mit anderen starken Mathe-Tools verbinden, wie zum Beispiel:

• SageMath – ein umfangreiches Mathematiksystem, das SymPy als Backend nutzt.
• SymEngine – eine schnellere C++-Neuimplementierung des Kerns von SymPy.
• Pyomo – macht Optimierungsmodellierung möglich(siehe Optimierung mit Pyomo).

Gemeinschaft, Beitrag und Entwicklung

SymPy ist erfolgreich, weil es eine starke Open-Source-Community hat. Eine weltweite Gruppe von Entwicklern, Forschern, Lehrern und Studenten arbeitet an SymPy und macht es jeden Tag besser und stabiler. Jeder kann helfen, Fragen stellen oder mitmachen, ohne dass man eine Erlaubnis oder eine Firmenmitgliedschaft braucht.

Beitrag und Entwicklung

Leute, die helfen wollen, machen normalerweise einen Fork des Repositorys, nehmen Änderungen vor, führen die Testsuite mit „ pytest “ aus und schicken dann einen Pull-Request zur Überprüfung.

Um sicherzugehen, dass jede Änderung zuverlässig ist, wird sie einem Code-Review-Prozess unterzogen. Das Projekt hat auch ein Test-Framework, damit Leute Tests auf ihren eigenen Rechnern machen können, bevor sie was einreichen. 

Fehler melden und Support suchen

Für Fehler oder Hilfe:

• Probleme auf GitHub unter SymPy Issuesmelden
• Frag auf Stack Overflow 
• Tritt der SymPy-Gitter-Gruppe oder der Mailingliste bei

Je genauer du das Problem erklärst, einschließlich des Codes, deiner Erwartungen, der tatsächlichen Ergebnisse und der von dir verwendeten SymPy-Version, desto schneller kann dir die Community helfen. 

Zukünftige Ausrichtung

SymPy entwickelt sich immer weiter, und es wird weiter daran gearbeitet, seine Funktionen zu erweitern, seine Leistung zu verbessern und es mit KI-Tools zu verbinden. Es gibt auch Bestrebungen, die Codegenerierung, Dokumentation und den Einsatz im Bildungsbereich zu verbessern. Neue Mitwirkende sind besonders willkommen, um bei der Sortierung der Fehler und Probleme zu helfen, die Dokumentation zu verbessern und neue Funktionen für symbolische Mathematik hinzuzufügen.

Fazit

SymPy ist eine echt coole Bibliothek, mit der du symbolische Mathematik in Python nutzen kannst. Das macht es nützlich für Bildung, Forschung und sogar für Ingenieursarbeiten in der echten Welt. Es bietet ein Open-Source-Ökosystem, in dem du verschiedene mathematische und algebraische Operationen und Transformationen durchführen kannst. SymPy ist ein Tool, das sich Schüler, Entwickler und Forscher mal anschauen sollten. Also los geht's – öffne ein Jupyter-Notebook, importiere sympy und fang an zu entdecken. 

Du kannst auch die folgenden Quellen für weitere Infos checken:

• SciPy-Spickzettel: Lineare Algebra in Python
• SymPy-Dokumentation
• Wie man eine Zahl in Python quadriert