SymPy : Guide complet des mathématiques symboliques en Python

Si vous avez déjà souhaité que Python puisse effectuer et exprimer des opérations algébriques comme un mathématicien, SymPy est la solution qu'il vous faut.

SymPy signifie Symbolic Python. Il s'agit d'une bibliothèque conçue pour effectuer des calculs symboliques, ce qui signifie qu'elle peut développer, simplifier, dériver et résoudre des équations de manière symbolique, comme vous le feriez sur papier.  Une extension importante est que les expressions mathématiques contenant des variables non évaluées sont conservées sous forme symbolique. Par exemple, la racine carrée de huit sera représentée par 2*sqrt(2), au lieu de l'approximer à 2,828.   

Parmi les principaux avantages de SymPy, on peut citer le fait qu'il s'agit d'un logiciel open source, entièrement écrit en Python, et qu'il est compatible avec d'autres bibliothèques Python. 

Principaux avantages de Sympy. Source : Image fournie par Napkin AI

Brève histoire de SymPy

SymPy est né d'une idée simple : rendre le calcul symbolique accessible à tous.

Il a été lancé en 2006 par Ondřej Čertík, étudiant à l'université du Nevada. Il souhaitait créer une bibliothèque mathématique symbolique légère et flexible en Python pur afin que les utilisateurs n'aient pas à gérer la complexité des grands systèmes d'algèbre informatique tels que Maple ou Mathematica. 

Entre 2007 et 2010, SymPy a connu une croissance rapide grâce à sa participation au Google Summer of Code, au cours duquel les principaux modules de base tels que la simplification, la résolution et le calcul ont été considérablement développés. 

Vers 2012, SymPy avait atteint un niveau de maturité tel qu'il a été intégré à SageMath, ce qui a marqué sa reconnaissance en tant que backend symbolique fiable au sein de l'écosystème scientifique Python au sens large. À ce jour, SymPy a évolué au-delà de son utilisation en algèbre vers des domaines avancés tels que la physique, la géométrie, la combinatoire, la génération de code et les outils de compilation axés sur les performances.

Premiers pas avec SymPy

Avant d'explorer les fonctionnalités avancées de SymPy, veuillez vous assurer de l'avoir correctement configuré.

Installation et configuration

La méthode la plus simple pour installer SymPy, qui est également la méthode recommandée, consiste à utiliser pip :

pip install sympy

Si vous utilisez Conda, la commande est la suivante :

conda install sympy

Vous pouvez également procéder à l'installation directement à partir du code source (ceci est particulièrement utile pour les contributeurs) :

git clone https://github.com/sympy/sympy.git

Si vous avez des questions concernant les dépendances : SymPy fonctionne entièrement sous Python et ne dépend d'aucune bibliothèque externe. Des paquets optionnels tels que mpmath peuvent être installés pour l'arithmétique à précision arbitraire :

pip install mpmath

Vérification de l'installation

Pour vérifier l'installation, veuillez ouvrir Python et saisir :

import sympy
print(sympy.__version__)

1.14.0

La sortie affiche la version installée du paquet.  Vous pouvez maintenant tester le package à l'aide d'une expression simple :

from sympy import symbols

# Define x as a symbolic variable
x = symbols('x')

print((x + 2)**2)

(x + 2)**2

En ce qui concerne le dépannage :

• Si vous constatez l'erreur « ModuleNotFoundError », veuillez relancer « pip install sympy ».

• En cas de conflits de versions, veuillez mettre à jour pip : pip install --upgrade pip

Il est également important de savoir que : Si vous pensez qu'il y a un bug ou si vous souhaitez demander une fonctionnalité, vous pouvez également ouvrirun ticket. Pour plus de détails sur les méthodes d'installation, veuillez consulter la documentation officielle.

Utilisation de base

SymPy offre un environnement interactif dans lequel vous pouvez manipuler symboliquement des expressions algébriques.

from sympy import symbols, expand

#define x and y as symbolic variables
x, y = symbols('x y')

# create an algebraic expression
expr = (x + y)**2

expanded = expand(expr)
print(expanded)

x**2 + 2*x*y + y**2

Le résultat imprimé ci-dessus x**2 + 2*x*y + y**2 est la forme entièrement développée, démontrant comment SymPy effectue une algèbre symbolique exacte plutôt qu'un calcul numérique.

Caractéristiques et fonctionnalités principales

Les fonctionnalités principales sont axées sur le calcul symbolique, ce qui implique de travailler avec des fonctions, des équations et des expressions en tant que symboles plutôt qu'en tant que nombres.

Opérations arithmétiques

Vous pouvez traiter les variables symboliques comme des variables algébriques. De plus, les fonctions peuvent passer d'un formulaire à un autre, comme le montre le code ci-dessous. 

En utilisant expand() pour la distribution et factor() pour la simplification inverse, SymPy effectue la transformation entre les formes développées et factorisées d'une expression algébrique.

from sympy import symbols, expand, factor

# Define symbolic variables x and y
x, y = symbols('x y')

# Create an algebraic expression
expr = (x + y)**2

# Expand the expression to its full polynomial form
print(expand(expr))  

# Factor the expanded polynomial back into its compact form
print(factor(x**2 + 2*x*y + y**2)) 

x**2 + 2*x*y + y**2
(x + y)**2

Techniques de simplification

La simplification est essentielle au calcul symbolique. Sympy dispose d'une fonction générale, appelée « simplify() », qui permet de simplifier facilement les expressions rationnelles, trigonométriques ou algébriques.

from sympy import simplify, trigsimp, sin, cos

# Create a trigonometric expression
expr = sin(x)**2 + cos(x)**2

# General simplification — recognizes that sin²x + cos²x = 1
print(simplify(expr)) 

# Trigonometric-specific simplification — also simplifies to 1
print(trigsimp(expr)) 

Le résultat des fonctions simplify() et trigsimp() ci-dessus est égal à un. 

Opérations de calcul

SymPy est particulièrement adapté au calcul différentiel et intégral, car il permet d'effectuer des dérivées, des intégrales, des limites et même des développements en série de manière symbolique, comme si l'on effectuait les calculs à la main, mais avec une précision parfaite.

Différenciation

Pour calculer des dérivées, veuillez utiliser la fonction diff().

from sympy import diff

# Define a symbolic polynomial expression
f = x**3 + 2*x**2 + x

# Compute the derivative of the expression with respect to x
df = diff(f, x)
print(df)

3*x**2 + 4*x + 1

Intégration

Le code ci-dessous calcule l'intégrale indéfinie de l'expression symbolique f par rapport à la variable x à l'aide de la fonction integrate() de SymPy. La primitive obtenue est ensuite affichée.

from sympy import integrate

# Compute the indefinite integral of the expression f with respect to x
integral = integrate(f, x)
print(integral)

x**4/4 + 2*x**3/3 + x**2/2

Limites

Le calcul de la limite est une opération classique de calcul différentiel, qui peut être effectuée à l'aide de la fonction limit() de SymPy. La syntaxe est la suivante : limit(f(x), x, x0).  Par exemple, le code ci-dessous calcule la limite de l'expression sin(x)/x lorsque x tend vers zéro et affiche le résultat exact, one. 

from sympy import limit, sin

# Compute the limit of sin(x)/x as x approaches 0 
limit_expr = limit(sin(x)/x, x, 0)
print(limit_expr) 

Développement en série

La fonction series() permet de calculer le développement en série de Taylor ou en série entière d'une expression mathématique autour d'un point donné.

from sympy import series, exp

# Generate the Taylor series expansion of e^x around 0 up to 5 terms
print(series(exp(x), x, 0, 5))

1 + x + x**2/2 + x**3/6 + x**4/24 + O(x**5)

Summations

La fonction summation() dans SymPy effectue une sommation symbolique exacte sur une certaine plage, tout comme la notation sigma en mathématiques.

from sympy import summation, symbols

# Compute the symbolic sum of 1/n^2 from n = 1 to 5
n = symbols('n')
print(summation(1/n**2, (n, 1, 5)))  

5269/3600

Résolution d'équations

SymPy facilite la résolution d'équations symboliques, non seulement les équations algébriques simples, mais également les systèmes d'équations, les équations différentielles et même les équations diophantiennes, qui n'ont que des nombres entiers comme solutions. 

Il dispose de puissants solveurs tels que 

• solve() pour les équations algébriques, 

• linsolve() pour les systèmes linéaires, et 

• dsolve() pour les équations différentielles qui fournissent des solutions exactes lorsque cela est possible. 

Équations algébriques

from sympy import Eq, solve
# Define and solve the equation x^2 - 4 = 0 symbolically
eq = Eq(x**2 - 4, 0)

print(solve(eq, x)) 

[-2, 2]

Systèmes d'équations

from sympy import linsolve, symbols

# Solve a system of linear equations:
# x + y = 5  and  x - y = 1
x, y = symbols('x y')
sol = linsolve([x + y - 5, x - y - 1], (x, y))

print(sol) # Outputs the solution as a set (x, y)

{(3, 2)}

Équations différentielles

from sympy import Function, dsolve

# Define y as a symbolic function of x
y = Function('y')

# Define a second-order differential equation
diff_eq = Eq(y(x).diff(x, 2) - y(x), 0)

# Solve the differential equation symbolically
print(dsolve(diff_eq))

Eq(y(x), C1*exp(-x) + C2*exp(x))

Opérations matricielles

SymPy est un excellent outil pour l'algèbre linéaire, car il prend en charge les matrices symboliques. Vous pouvez facilement travailler avec des matrices et effectuer des opérations mathématiques telles que l'addition et la multiplication, comme vous le feriez en algèbre classique. 

from sympy import Matrix

# Define symbolic matrices A and B
A = Matrix([[1, 2], [x, 3]])
B = Matrix([[x], [4]])

# Perform matrix multiplication
print(A * B)

Matrix([[x + 8], [x**2 + 12]])

Opérations avancées

SymPy vous permet également de calculer symboliquement des propriétés matricielles importantes telles que les déterminants, les inverses, les valeurs propres et les vecteurs propres, vous fournissant ainsi des réponses exactes. 

# Compute the determinant of matrix A
A.det()      

# Compute the inverse of matrix A
A.inv()      

# Compute the eigenvalues of matrix A
A.eigenvals() 

{2 - sqrt(2*x + 1): 1, sqrt(2*x + 1) + 2: 1}

Capacités graphiques

SymPy ne se limite pas au calcul symbolique, il prend également en charge la visualisation d'expressions mathématiques. Grâce aux utilitaires de traçage intégrés, vous pouvez générer des graphiques en 2D et même en 3D de fonctions symboliques à l'aide de quelques lignes de code. 

Par exemple, le code ci-dessous génère un graphique en 2D :  

from sympy.plotting import plot


# Plot the function x^2 over the range -5 to 5
plot(x**2, (x, -5, 5))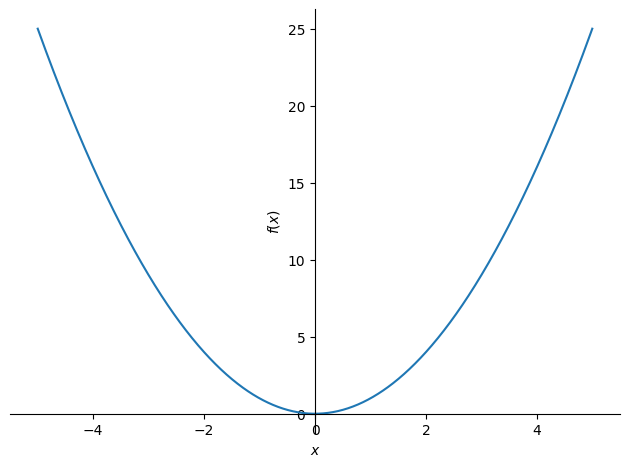

Graphique 2D généré à l'aide de SymPy. 

Pour générer des graphiques en 3D, vous pouvez utiliser la fonction plot3d() comme indiqué ci-dessous.

from sympy.plotting import plot3d
from sympy import sin

# Generate a 3D surface plot of the function sin(x*y) over the specified x and y ranges
plot3d(sin(x*y), (x, -5, 5), (y, -5, 5))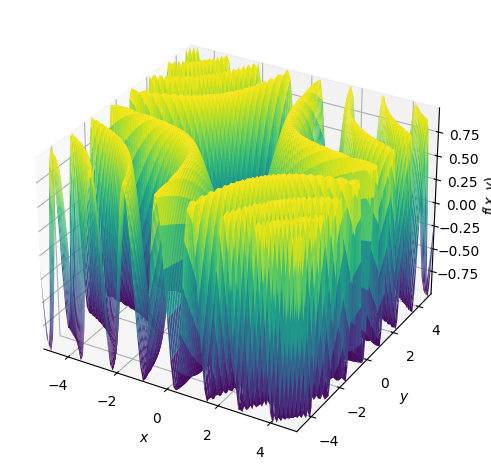

Capacité de graphisme 3D de SymPy

Si vous avez besoin d'un contrôle ou d'une mise en forme plus poussés, SymPy peut également s'intégrer à Matplotlib pour permettre des visualisations entièrement personnalisables. Pour des visualisations plus avancées, veuillez consulter notre tutoriel sur Plotly Shapes.

Fonctionnalités avancées

SymPy va bien au-delà de l'algèbre de base : il s'étend aux polynômes, à la combinatoire et même à la physique.

Manipulation de polynômes

Vous pouvez facilement définir et manipuler des polynômes. Le code ci-dessous crée un objet polynôme à partir de l'expression, puis affiche son degré et sa forme factorisée avec les coefficients à l'aide de la fonction SymPy Poly(). 

from sympy import Poly

# Create a symbolic polynomial in variable x
p = Poly(x**3 - 3*x**2 + x - 3, x)

# Print the degree of the polynomial (highest power of x)
print(p.degree())  

# Print the factorized form of the polynomial along with coefficients
print(p.factor_list())  

3
(1, [(Poly(x - 3, x, domain='ZZ'), 1), (Poly(x**2 + 1, x, domain='ZZ'), 1)])

Pour les systèmes polynomiaux complexes, les bases de Gröbner sont prises en charge. Il s'agit d'une version simplifiée et standardisée d'un système d'équations polynomiales, ce qui facilite leur résolution. 

Par exemple, le code ci-dessous calcule la base de Gröbner pour le système polynomial [x*y - 1, y - x], ce qui signifie qu'il réécrit les équations sous une forme plus simple et plus structurée, plus facile à résoudre. Le résultat montre que le système est équivalent aux équations plus claires x = y et y² = 1, qui peuvent désormais être résolues directement.

from sympy import groebner, symbols

# Define x and y as symbolic variables
x, y = symbols('x y')

# Compute the Gröbner basis for the system of polynomial equations
print(groebner([x*y - 1, y - x], x, y))

GroebnerBasis([x - y, y**2 - 1], x, y, domain='ZZ', order='lex')

Combinatoire, mathématiques discrètes et théorie des nombres

SymPy dispose de plusieurs utilitaires qui lui permettent de traiter des problèmes combinatoires et de théorie des nombres. 

Par exemple, dans le code ci-dessous :

• La fonction binomial(5, 2) calcule le nombre de façons de choisir 2 éléments parmi 5 (un problème de combinaison). 

• factorial(6) calcule 6!, une opération courante dans les permutations. 

• isprime(19) vérifie si 19 est un nombre premier, et 

• factorint(100) renvoie sa factorisation exacte en nombres premiers sous la forme {2: 2, 5: 2}. 

from sympy import binomial, factorial, isprime, factorint
print(binomial(5, 2))   # 10
print(factorial(6))     # 720
print(isprime(19))      # True
print(factorint(100))   # {2: 2, 5: 2}

10
720
True
{2: 2, 5: 2}

10
720
True
{2: 2, 5: 2}

Ensemble, ces fonctions illustrent la manière dont SymPy traite les mathématiques discrètes avec aisance et précision. Vous pouvez également travailler directement avec des partitions, des permutations et des combinaisons.

Applications en géométrie et en physique

SymPy n'est pas uniquement destiné à l'algèbre et au calcul ; il propose également des modules spécifiques pour la géométrie et la physique. 

Dans le module Géométrie, vous pouvez définir des objets mathématiques tels que des points, des lignes, des cercles et des polygones. À l'aide de symboles, vous pouvez également obtenir des équations de droites, d'intersections, de distances et de points médians. 

Par exemple, pour créer deux points et tracer une ligne entre eux, procédez comme suit :

from sympy import Point, Line, Circle

# Define two points and create a line passing through them
A, B = Point(0, 0), Point(1, 1)
L = Line(A, B)

# Print the symbolic equation of the line
print(L.equation())  

-x + y

En plus de ses capacités géométriques, SymPy fournit un module physique très utile. Ce module vous permet de modéliser la mécanique classique, les systèmes quantiques, les unités et les tailles.  Cela s'applique aussi bien lorsque vous utilisez des mètres par seconde pour calculer la vitesse que lorsque vous résolvez des équations de mouvement à l'aide de symboles. 

from sympy.physics.units import meter, second

# Define a symbolic physical quantity: velocity = 10 meters per second
velocity = 10 * meter / second
print(velocity)

10*meter/second

Impression et sortie LaTeX

SymPy vous permet d'imprimer des expressions symboliques dans plusieurs formats, notamment :

• Impression esthétique et conviviale 
• Sortie basée sur Unicode, et 
• LaTeX, qui est le langage de formatage standard utilisé dans les articles de recherche et la documentation scientifique. 

Vous pouvez utiliser des fonctions telles que pprint() pour rendre vos équations plus claires et plus professionnelles dans un notebook Jupyter ou lors de la création d'un rapport. Vous pouvez également utiliser latex() pour les préparer à la rédaction d'un article de recherche. Cela vous évite d'avoir à tout formater vous-même.

from sympy import pprint, latex, symbols

# Define x and y as symbolic variables
x, y = symbols('x y')

# Now you can perform symbolic math operations
expr = (x+y)**3

# Pretty print to the console
pprint(expr)

# Print the LaTeX string
print(latex(expr))

     3
(x + y) 
\left(x + y\right)^{3}

Génération de code et optimisation des performances

Bien que SymPy excelle dans le calcul symbolique, il permet également de convertir des expressions symboliques en code exécutable optimisé pour une utilisation numérique haute performance.

Le code ci-dessous utilise l'utilitaire codegen() de SymPy pour générer automatiquement du code en langage C à partir d'une expression symbolique, le rendant ainsi prêt à être utilisé dans des applications embarquées.

from sympy.utilities.codegen import codegen

# Generate C code for the symbolic function and save it as 'output'
codegen(("f", x**2 + 1), "C", "output")

[('output.c',
  '/******************************************************************************\n *                      Code generated with SymPy 1.14.0                      *\n *                                                                            *\n *              See http://www.sympy.org/ for more information.               *\n *                                                                            *\n *                       This file is part of \'project\'                       *\n ******************************************************************************/\n#include "output.h"\n#include <math.h>\n\ndouble f(double x) {\n\n   double f_result;\n   f_result = pow(x, 2) + 1;\n   return f_result;\n\n}\n'),
 ('output.h',
  "/******************************************************************************\n *                      Code generated with SymPy 1.14.0                      *\n *                                                                            *\n *              See http://www.sympy.org/ for more information.               *\n *                                                                            *\n *                       This file is part of 'project'                       *\n ******************************************************************************/\n\n\n#ifndef PROJECT__OUTPUT__H\n#define PROJECT__OUTPUT__H\n\ndouble f(double x);\n\n#endif\n\n")]

Lambdify

La fonction d'lambdify() ion convertit les expressions symboliques en fonctions Python numériques rapides. Par exemple, le code ci-dessous utilise lambdify pour convertir l'expression symbolique stockée sous l'objet f en une fonction Python rapide compatible avec NumPy. Lorsqu'il est évalué sur le tableau [1, 2, 3], il renvoie [4, 9, 16]. 

from sympy import lambdify
import numpy as np

# Convert the symbolic expression into a fast numerical function using NumPy
f = lambdify(x, x**2 + 2*x + 1, 'numpy')

# Evaluate the function on a NumPy array
print(f(np.array([1, 2, 3])))

[ 4  9 16]

Considérations relatives aux performances

Étant donné que SymPy se concentre sur la précision symbolique, il peut être plus lent que les calculs numériques. Cela étant dit, il existe plusieurs méthodes pour améliorer les performances lorsque l'on travaille avec des expressions volumineuses ou complexes. 

Par exemple, vous pouvez utiliser lambdify() pour transformer des expressions symboliques en fonctions numériques rapides qui fonctionnent bien avec NumPy, ou vous pouvez les simplifier avant de les évaluer. 

Vous pouvez accélérer davantage les calculs lourds en utilisant des techniques telles que l'élimination des sous-expressions communes, la compilation automatique de code et l'intégration avec des outils externes tels que Numba ou Cython.

SymPy dans l'écosystème Python

SymPy ne fonctionne pas de manière isolée : il s'intègre parfaitement aux autres outils populaires utilisés dans les domaines de la science des données, de l'éducation et de la recherche, et s'inscrit parfaitement dans l'écosystème scientifique Python au sens large.

Intégration avec d'autres bibliothèques

Vous pouvez associer SymPy avec :

• NumPy/SciPy pour des calculs numériques de haute performance
• Matplotlib pour la visualisation
• Pandas pour l'analyse symbolique des données

import numpy as np
from sympy import lambdify

# Convert the symbolic expression x^2 into a fast NumPy-compatible function
f = lambdify(x, x**2, 'numpy')

# Evaluate the function on a NumPy array from 0 to 4
print(f(np.arange(5)))

[ 0  1  4  9 16]

Applications éducatives

SymPy est largement utilisé dans les salles de classe et les environnements d'auto-apprentissage, car il reflète la manière dont les mathématiques sont enseignées sur papier, étape par étape et de manière symbolique. Dans Jupyter Notebooks, les étudiants peuvent expérimenter en direct des équations d'algèbre, de calcul ou de physique et obtenir des résultats symboliques exacts au lieu d'approximations approximatives. Veuillez consulter l'aide-mémoire Jupyter Notebook pour commencer.

Projets connexes et intégrations

SymPy s'intègre également parfaitement à d'autres outils mathématiques performants, tels que :

• SageMath — un système mathématique à grande échelle utilisant SymPy comme backend.
• SymEngine — une réimplémentation plus rapide en C++ du cœur de SymPy.
• Pyomo — intègre la modélisation d'optimisation(voir Optimisation avec Pyomo).

Communauté, contribution et développement

SymPy prospère grâce à une communauté open source solide. Un groupe international de développeurs, chercheurs, enseignants et étudiants travaille sur SymPy, le rendant chaque jour plus performant et plus robuste. Toute personne peut apporter son aide, poser des questions ou s'impliquer sans avoir besoin d'une autorisation ou d'une adhésion à l'entreprise.

Contribution et développement

Les personnes souhaitant contribuer doivent généralement créer une fourche du dépôt, apporter des modifications, exécuter la suite de tests à l'aide de la commande ` pytest`, puis envoyer une pull request pour examen.

Afin de garantir la fiabilité de chaque modification, celle-ci est soumise à un processus de révision du code. Le projet dispose également d'un cadre de test permettant aux contributeurs d'effectuer des tests sur leurs propres machines avant de soumettre leurs contributions. 

Signaler des bogues et demander de l'assistance

Pour signaler des erreurs ou obtenir de l'aide :

• Veuillez signaler les problèmes sur GitHub sous SymPy Issues.
• Veuillez poser votre question sur Stack Overflow. 
• Veuillez rejoindre le groupe SymPy Gitter ou la liste de diffusion.

Plus vous expliquerez clairement le problème, en incluant le code, ce que vous attendiez, ce qui s'est réellement produit et la version de SymPy que vous utilisez, plus la communauté pourra vous aider rapidement. 

Orientations futures

SymPy continue de se développer, et des travaux sont toujours en cours pour étendre ses fonctionnalités, améliorer ses performances et l'intégrer à des outils d'intelligence artificielle. Des efforts sont également déployés pour améliorer la génération de code, la documentation et l'utilisation à des fins éducatives. Les nouveaux contributeurs sont particulièrement bienvenus pour aider à trier les bogues et les problèmes, améliorer la documentation et ajouter de nouvelles fonctionnalités pour les mathématiques symboliques.

Conclusion

SymPy est une bibliothèque puissante qui permet d'utiliser les mathématiques symboliques en Python. Cela le rend utile pour l'éducation, la recherche et même les travaux d'ingénierie dans le monde réel. Il fournit un écosystème open source, au sein duquel il est possible d'effectuer diverses opérations et transformations mathématiques et algébriques. SymPy est un outil que les étudiants, les développeurs et les chercheurs devraient envisager d'utiliser. N'hésitez pas à ouvrir un notebook Jupyter, à importer sympy et à commencer votre exploration. 

Vous pouvez également consulter les ressources suivantes pour approfondir vos connaissances :

• Aide-mémoire SciPy : Algèbre linéaire en Python
• Documentation SymPy
• Comment élever un nombre au carré en Python